フレネル積分

フレネル積分の形にはいくつかありますが、ここでは

\[\int_0^\infty \cos t^3 dt = \frac{1}{2} \int_0^\infty (e^{it^3} + e^{-it^3}) \tag{1}\]

を求めていきましょう。まず関数$f(z) = e^{iz^3} \ (z = x + iy)$を複素数平面上で閉曲路積分します。

\[\left\{ \begin{array}{ccc} C_1 &:& x = 0 \rightarrow R \\ C_2 &:& z = R e^{i\theta} \ (\theta = 0 \rightarrow \pi/6) \\ C_3 &:& z = r e^{i\frac{\pi}{6}} \ (r = R \rightarrow 0) \\ C_4 &:& z = R e^{i\theta} \ (\theta = 0 \rightarrow \pi/6) \\ C_5 &:& z = r e^{-i\frac{\pi}{6}} \ (r = R \rightarrow 0) \end{array} \right.\]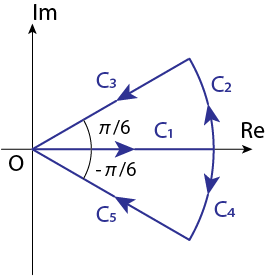

$フレネル積分を求めるための複素数平面での積分経路。$

Cauchyの積分定理より

\[\begin{aligned} &\oint_{C_1 + C_2 + C_3} f(z) dz = \int_0^R e^{ix^3} dx + \int_0^{\pi/6} e^{iR^3 e^{3i\theta}} iR e^{i\theta} d\theta + \int_R^0 e^{ir^3 e^{i\frac{\pi}{2}}} e^{i\frac{\pi}{6}} dr = 0 \\ &\underbrace{\Longrightarrow}_{R \rightarrow \infty} \ \int_0^\infty e^{ix^3} dx = \int_0^\infty e^{-r^3} e^{i \frac{\pi}{6}} dr - \lim_{R \rightarrow \infty} \int_0^{\pi/6} i R e^{i\theta} e^{iR^3 \cos 3\theta} \underbrace{e^{-R^3 \sin 3\theta}}_{\rightarrow 0 (\sin 3 \theta > 0)} d\theta = e^{i \frac{\pi}{6}} \int_0^\infty e^{-r^3} dr \end{aligned}\]

今度は$g(z) = e^{-iz^3}$を$C_1, C_4, C_5$の閉曲路積分をします。同様にCauchyの積分定理より

\[\begin{aligned} &\oint_{C_1 + C_4 + C_5} g(z) dz = \int_0^R e^{-ix^3} dx + \int_0^{-\pi/6} e^{-iR^3 e^{3i\theta}} iR e^{i\theta} d\theta + \int_R^0 e^{-ir^3 e^{i\frac{\pi}{2}}} e^{-i\frac{\pi}{6}} dr = 0 \\ &\underbrace{\Longrightarrow}_{R \rightarrow \infty} \ \int_0^\infty e^{-ix^3} dx = \int_0^\infty e^{-r^3} e^{-i \frac{\pi}{6}} dr - \lim_{R \rightarrow \infty} \int_0^{-\pi/6} i R e^{i\theta} e^{-iR^3 \cos 3\theta} \underbrace{e^{R^3 \sin 3\theta}}_{\rightarrow 0 (\sin 3 \theta < 0)} d\theta = e^{-i \frac{\pi}{6}} \int_0^\infty e^{-r^3} dr \end{aligned}\]

以上より

\[\int_0^\infty \cos t^3 dt = \underbrace{\frac{1}{2} (e^{i\frac{\pi}{6}} + e^{-i \frac{\pi}{6}})}_{= \cos \frac{\pi}{6}} \int_0^\infty e^{-r^3} dr \underbrace{=}_{t=r^3} \frac{\sqrt{3}}{2} \int_0^\infty e^{-t} \frac{dt}{3t^{2/3}} = \frac{1}{2 \sqrt{3}} \int_0^\infty t^{\frac{1}{3}-1} e^{-t} dt = \frac{1}{2\sqrt{3}} \Gamma \left( \frac{1}{3} \right) \tag{2}\]

途中、ガンマ関数を用いました。ちなみに同様のやり方すれば

\[\int_0^\infty \sin t^3 dt = \frac{1}{2i} \int_0^\infty (e^{it^3}-e^{-it^3}) dt = \frac{1}{2i} (e^{i\frac{\pi}{6}} - e^{-i\frac{\pi}{6}}) \int_0^\infty e^{-r^3} dr = \frac{1}{6} \Gamma \left( \frac{1}{3}\right)\]

も求めることができます。