Table of contents
密度波理論 (density wave theory)
ここでは、銀河の渦巻構造を形成する理論として提唱された、密度波理論についてメモしています。
巻き込み困難 (winding dillemma)
渦巻構造を持つ円盤銀河の回転速度は、円盤内では\(v_c \sim (定数)\)のようなflat rotationと呼ばれる特徴を持ちます。 しかしこの場合、角速度は\(\Omega \propto r^{-1}\)となります。 これは渦巻銀河の内側ほど、角速度が大きいことを意味します。 もし渦巻を形成しているのが実体を持ったものの場合、内側ほど早く回転し、巻き込みが時間とともにきつくなってしまいます。 天の川銀河の場合には200-300万年ほどで円盤が一回転すると考えられており、数億年も時間が経てば、渦巻がきつく巻いてしまいます。 そのような巻き込みがきつい渦巻銀河は見つかっていないことから、これは巻き込み困難と呼ばれています。
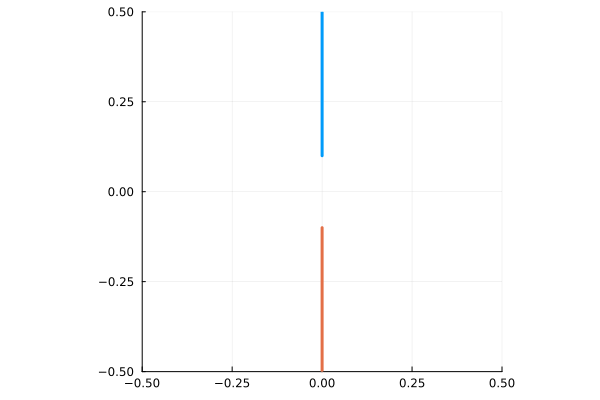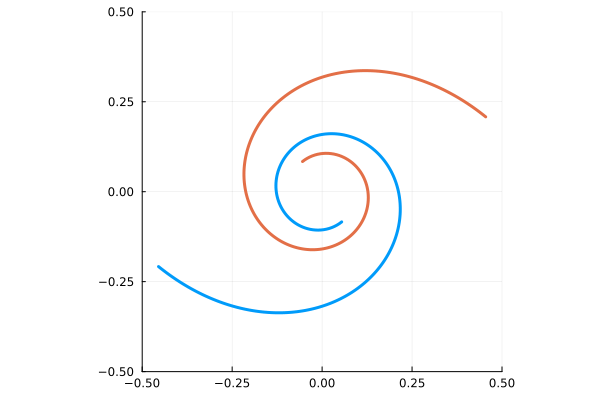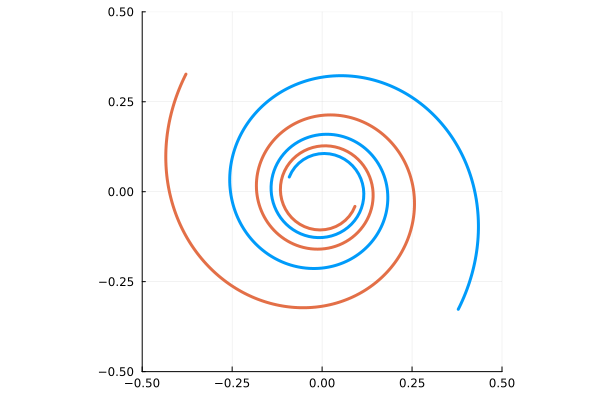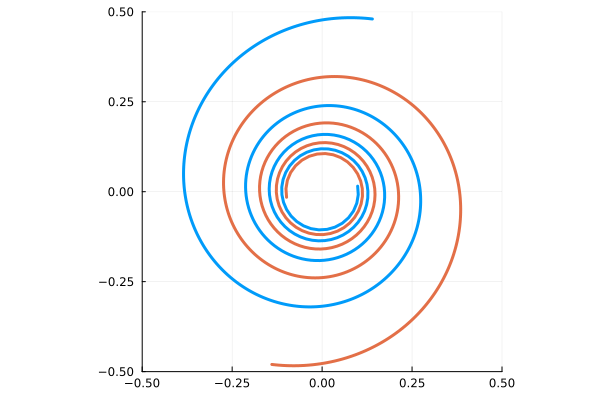
2本の渦状腕の巻きつきが、時間とともにキツくなっていく様子。
渦状腕部分がガスや恒星の自己重力により形成されたものとし、そのようにしてできた密度超過領域が差動回転で引き延ばされた構造の場合、これは巻き込み困難の問題を受けることになります。
この問題を解消するために提案されたものが、密度波理論です。 この理論では、渦状腕の構成要素は入れ替わり立ち替わり変化します。 渦状腕の部分は波動のある位相の部分を表しているため、渦状腕の角速度(以降ではパターン速度と呼びます)とそれを形成する媒質の速度は同じではありません。 そのため、渦状腕は巻き込まれることなく、波動として同じ構造を維持し続けることが可能となります。
運動学的な密度波 (kinematic density waves)
ここでは、銀河円盤内を運動する一つの恒星の運動に着目してみましょう。 この恒星は銀河中心の周りを角速度\(\Omega\)で円運動しながら、エピサイクリック運動により動径方向に振動数\(\kappa\)で振動します。 静止系では、その軌道は一般にバラの花形(rosette)軌道を描き、閉じることはありません。 しかし、この恒星の運動を、角速度\(\Omega_p \equiv \Omega - \kappa /2\)で回転する座標系から見てみましょう。 この回転系から見ると、恒星は回転方向には角速度\(\Omega - \Omega_p = \kappa / 2\)で回転(公転)することになります。 \((公転角振動数):(動径方向角振動数)=1:2\)より、この回転系で公転運動を1回する間に、動径方向には2回振動を行うことになります。 つまりこの軌道は楕円を描いて閉じることになります。 この楕円を静止系から見ると、楕円の軸が角速度\(\Omega_p\)で回転して見えることになります。

様々な半径を運動する恒星に対してこの楕円軌道を考えると、上図のようになります。 この楕円の長軸が全て揃っている場合、上左図のように特別な変化は見られません。 しかし、長軸が少しずつづれていると、上真ん中図や上右図のような軌道の密な場所が渦巻状に現れます。 この渦巻構造は、静止系では角速度\(\Omega_p\)で回転しているように見えます。
ここまでは\(\Omega_p = \Omega - \kappa / 2\)の場合のみを考えてきましたが、一般には軌道が閉じる条件は
のように書けます。 ここで\(\Delta \varphi_p\)と\(\Delta \varphi\)はそれぞれ、\(\Omega_p\)で回転する系と静止系での動径方向振動1回後の方位角方向の角度変化分、\(2\pi / \kappa\)はエピサイクリック運動による動径方向の振動周期、\(m, n\)は整数です。 先程の例では\(n=\pm 1, m=2\)としていました。 ここから、\(m\)が1周期の軌道運動中の動径方向振動回数であることもわかります。 \(\Delta \varphi\)の定義から
\[\Delta \varphi = \frac{2\pi}{\kappa} \Omega \tag{2}\]のように計算されるため
\[\Omega_p = \Omega - \frac{n}{m} \kappa \tag{3}\]を得ます。
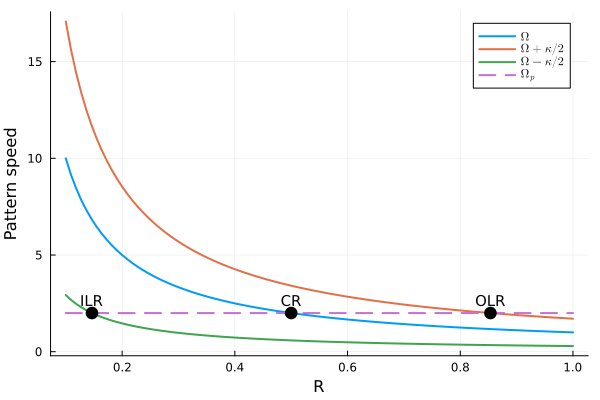
上図は\(\Omega - \kappa / 2, \Omega, \Omega + \kappa / 2\)、そして\(\Omega_p\)を描画したものです。 \(\Omega_p=(一定)\)の直線に対し、\(\Omega_p = \Omega - \kappa / 2, \Omega_p = \Omega, \Omega_p = \Omega + \kappa / 2\)の3つの交点があることが分かります。 \(\Omega_p = \Omega\)を共回転半径 (corotation radius)と呼びます。 \(\Omega_p = \Omega \pm \kappa / 2\)の2点をリンドブラッド共鳴点 (Lindblad resonance)と呼びますが、特に\(R\)が大きいものを外側リンドブラッド共鳴点(Outer Lindblad Resonance: OLR)、\(R\)が小さいものを内側リンドブラッド共鳴点(Inner Lindblad Resonance: ILR)などと呼びます。
ここまでの考え方には、運動する恒星どうしの重力相互作用が含まれておらず、また渦状腕ができたことによる非軸対称性が考慮されていません。 このことから恒星の軌道運動から作られた密度波を、運動学的密度波と呼びます。 また、ここでは\(\Omega_p\)を半径によらずに一定としています。 実際の銀河では\(\Omega_p\)が半径に依存し、楕円軌道の長軸方向は時事刻々とその向きを変えていくため、渦状腕が崩れていきます。 このことからもこの説明は完全ではないことが分かりますが、密度波理論がどういうものか、その特徴を良く捉えていることから、良く引き合いに出されます。
密度波理論
基礎方程式の線形化
ここからは、実際に密度波の分散関係式を求めることを考えましょう。 しかし一般的な銀河円盤の動力学には、数値計算が必要となります。 そこで、ここでは銀河円盤中を運動する恒星群を流体のように扱い、そのガスの分散関係式を求めます。 ガスの運動方程式は
\[\frac{\partial \mathbf{v}}{\partial t} + (\mathbf{v} \cdot \nabla) \mathbf{v} = - \frac{1}{\Sigma} \nabla P - \nabla \Phi \tag{4}\]のように書かれます。 ここで\(\mathbf{v} = (v_R, v_\varphi)\)は速度ベクトル、\(\Sigma\)は質量面密度、\(P\)は恒星円盤をガスと見立てた場合の熱運動による圧力、\(\Phi\)は重力ポテンシャルです。 この式の\(R\)成分は
\[\frac{\partial v_R}{\partial t} + v_R \frac{\partial v_R}{\partial R} + \frac{v_\varphi}{R} \frac{\partial v_R}{\partial \varphi} - \frac{v_\varphi^2}{R} = - \frac{\partial \Phi}{\partial R} - \frac{1}{\Sigma} \frac{\partial P}{\partial R} = - \frac{\partial}{\partial R} (\Phi + h) \tag{5}\]となります。 途中、\(P = K \Sigma^\gamma\)をのように状態方程式はポリトロープであるとし、さらにエンタルピー\(h\)を
\[h \equiv \int \frac{dP}{\Sigma (P)} \underbrace{=}_{dP = K\gamma \Sigma^{\gamma -1} d\Sigma} K \gamma \int \Sigma^{\gamma -2} d\Sigma = \frac{K\gamma}{\gamma -1} \Sigma^{\gamma -1} \tag{6}\]のように定義しました。 同様に\(\varphi\)成分は
\[\frac{\partial v_\varphi}{\partial t} + v_R \frac{\partial v_\varphi}{\partial R} + \frac{v_\varphi}{R} \frac{\partial v_\varphi}{\partial \varphi} + \frac{v_R v_\varphi}{R} = - \frac{1}{R} \frac{\partial \Phi}{\partial \varphi} - \frac{1}{\Sigma R} \frac{\partial P}{\partial \varphi} = - \frac{1}{R} \frac{\partial}{\partial \varphi} (\Phi + h) \tag{7}\]です。 さらに銀河円盤が無限に薄いと仮定すると、ポアソン方程式から
\[\nabla^2 \Phi = 4\pi G \Sigma \delta(z) \tag{8}\]の関係が成り立ちます。
ここで定常軸対称な平衡状態を0次とし、そこに摂動を加えた場合の応答を考えましょう。 定常軸対称より$\(\frac{\partial}{\partial t} = \frac{\partial}{\partial \varphi} =0\)のように考えることができます。 そしてこの平衡状態では、簡単のため円運動\(v_R =0\)であるとします。 平衡状態の物理量には0の添え字をつけることにすると、(5), (6), (8)式より
次に、摂動量に1次の添字をつけることにしましょう。
\[v_R = v_{R, 1} (R, \varphi, t), \quad v_\varphi = v_{\varphi, 0} + v_{\varphi, 1}, \quad h = h_0 + h_1, \quad \Phi = \Phi_0 + \Phi_1, \quad \Sigma = \Sigma_0 + \Sigma_1 \tag{12}\]より、(5), (9)式から
\[\frac{\partial v_{R, 1}}{\partial t} + v_{R, 1} \frac{\partial v_{R, 1}}{\partial R} + \frac{v_{\varphi, 0}+v_{\varphi, 1}}{R} \frac{\partial v_{R, 1}}{\partial \varphi} - \frac{(v_{\varphi, 0} + v_{\varphi, 1})^2}{R} = -\frac{\partial}{\partial R} (\Phi_0 + h_0 + \Phi_1 + h_1)\]ですが、摂動量は微小なので、その2乗を無視します。 そして(9)-(11)式より
\[\frac{\partial v_{R, 1}}{\partial t} + \Omega \frac{\partial v_{R, 1}}{\partial \varphi} - 2\Omega v_{\varphi, 1} = - \frac{\partial}{\partial R} (\Phi_1 + h_1) \tag{13}\]のように整理されます。 途中、\(\Omega = v_{\varphi, 0} / R\)としました。 同様に(7)式は
\[\frac{\partial v_{\varphi, 1}}{\partial t} + v_{R, 1} \left\{ \frac{d}{d R} (R \Omega) + \Omega \right\} + \Omega \frac{\partial v_{\varphi, 1}}{\partial \varphi} = - \frac{1}{R} \frac{\partial}{\partial \varphi} (\Phi_1 + h_1) \tag{14}\]のようになります。 ここで、摂動量は\(\varphi\)方向のフーリエモードを考えることにしましょう。 すなわち摂動量は
\[v_{R, 1} = v_{R, 1a} e^{i(m\varphi - \omega t)}, \quad v_{\varphi, 1} = v_{\varphi, 1a} e^{i(m\varphi - \omega t)}, \quad \Phi_1 = \Phi_{1a} e^{i(m\varphi - \omega t)}, \quad h_1 = h_{1a} e^{i(m\varphi - \omega t)}, \quad \Sigma_1 = \Sigma_{1a} e^{i(m\varphi - \omega t)} \tag{15}\]などのように書けるとし、振幅である\(v_{R, 1a}, v_{\varphi, 1a}, \Phi_1, h_1\)は\(R\)の関数とします。 すると\(\frac{\partial}{\partial t} \rightarrow -i \omega, \frac{\partial}{\partial \varphi} \rightarrow im\)のようになるため、(13)式は
\[-i\omega v_{R, 1} + im \Omega v_{R, 1} - 2\Omega v_{\varphi, 1} = - \frac{d}{dR} (\Phi_{1} + h_{1}) \tag{16}\]そして(14)式は
\[-i\omega v_{\varphi, 1} + v_{R, 1} \left\{\frac{d}{dR} (R\Omega) + \Omega \right\} + im \Omega v_{\varphi, 1} = -\frac{im}{R} (\Phi_{1} + h_{1}) \tag{17}\]となります。 ここでオールト定数\(B\)を用いると、\(\frac{d\Omega}{dR} + 2\Omega = -2B\)より
\[v_{\varphi, 1} = \frac{i}{\omega - m\Omega} \left\{ 2B v_{R, 1} - \frac{im}{R} (\Phi_{1} + h_{1}) \right\} \tag{18}\]となります。 これを(16)式に代入すると
\[\begin{align} &-i(\omega - m\Omega) v_{R, 1} = \frac{2i\Omega}{\omega - m\Omega} \left\{ 2B v_{R, 1} - \frac{im}{R} (\Phi_{1} + h_{1}) \right\} - \frac{d}{dR} (\Phi_{1} + h_{1}) \notag \\ &\Longrightarrow \ -i \frac{(\omega - m \Omega)^2 + 4\Omega B}{\omega - m \Omega} v_{R, 1} = \frac{2m \Omega}{R(\omega - m\Omega)} (\Phi_{1} + h_{1}) - \frac{d}{dR} (\Phi_{1} + h_{1}) \notag \end{align}\]となります。 \(\kappa^2 = -4\Omega B\)のように、エピサイクリック振動数を用いてさらに整理すると
\[v_{R, 1} = \frac{i}{\Delta} \left\{ (\omega -m \Omega) \frac{d}{dR} (\Phi_{1} + h_{1}) -\frac{2m\Omega}{R} (\Phi_{1} + h_{1})\right\} \tag{19}\]を得ます。 ここで\(\Delta \equiv \kappa^2 - (\omega -m\Omega)^2\)としました。 これを(18)式に代入すれば
\[\begin{align} v_{\varphi, 1} &= \frac{i}{\omega -m\Omega} \left[ \frac{2iB}{\Delta} \left\{ (\omega -m \Omega) \frac{d}{dR} (\Phi_{1} + h_{1}) -\frac{2m\Omega}{R} (\Phi_{1} + h_{1})\right\} - \frac{im}{R} (\Phi_{1} + h_{1})\right] \notag \\ &= -\frac{1}{\Delta} \left\{2B \frac{d}{dR} (\Phi_{1} + h_{1}) - \left(\frac{4m\Omega B}{R (\omega - m\Omega)} + \frac{m\Delta}{R(\omega - m\Omega)}\right) (\Phi_{1} + h_{1}) \right\} \notag \\ &= -\frac{1}{\Delta} \left\{2B \frac{d}{dR} (\Phi_{1} + h_{1}) + \frac{m(\omega -m\Omega)}{R} (\Phi_{1} + h_{1}) \right\} \tag{20} \end{align}\]となります。 もし\(\omega\)が実数なら、\(\Delta = 0\)となる半径が存在し、(19), (20)式が発散することになります。 このとき
\[\omega - m\Omega = \pm \kappa \ \Longrightarrow \ \Omega_p \equiv \frac{\omega}{m} = \Omega \pm \frac{\kappa}{m} \tag{21}\]となります。 ここで\(\Omega_p\)はパターン速度です。 これは(3)式において、\(n = \mp 1\)とした場合に相当することがわかります。 この場合は共鳴が生じ、小さな擾乱を用いた解析が破綻します。
ここからは、密度分布の擾乱\(\Sigma_1\)について求めることにしましょう。 (6)式より
です。 さらに状態方程式から、音速を計算しましょう。 すると
\[c_s^2 = \frac{dP}{d\Sigma} = K \gamma \Sigma^{\gamma -1} \tag{23}\]より(22)式は
\[h_1 = c_s^2 \frac{\Sigma_1}{\Sigma_0} \tag{24}\]のように整理されます。 ガスの連続の式は
\[\frac{\partial \Sigma}{\partial t} + \nabla \cdot (\Sigma \mathbf{v}) = 0 \tag{25}\]のように与えられます。 非摂動量\(\Sigma_0\)と摂動量\(\Sigma_1\)について考えると
\[\frac{\partial \Sigma_0}{\partial t} + \nabla \cdot (\Sigma_0 \mathbf{v}_0) = 0 \tag{26}\] \[\begin{align} &\frac{\partial}{\partial t} (\Sigma_0 + \Sigma_1) + \nabla \cdot \{ (\Sigma_0 + \Sigma_1) (\mathbf{v}_0 + \mathbf{v}_1) \} \approx \frac{\partial \Sigma_0}{\partial t} + \frac{\partial \Sigma_1}{\partial t} + \nabla \cdot \{ \Sigma_0 ( \mathbf{v}_0 + \mathbf{v}_1) \} + \nabla \cdot ( \Sigma_1 \mathbf{v}_0 ) = 0 \notag \\ &\underbrace{\Longrightarrow}_{(26)} \ \frac{\partial \Sigma_1}{\partial t} + \nabla \cdot (\Sigma_0 \mathbf{v}_1) + \nabla \cdot (\Sigma_1 \mathbf{v}_0) = 0 \tag{27} \end{align}\]円筒座標における発散より
\[\nabla \cdot (\Sigma_0 \mathbf{v}_1) = \frac{1}{R} \left\{ \frac{\partial}{\partial R} (R \Sigma_0 v_{1R}) + \frac{\partial}{\partial \varphi} (\Sigma_0 v_{1\varphi}) + R \frac{\partial}{\partial z} (\Sigma_0 v_{1z})\right\} = \frac{1}{R} \frac{\partial}{\partial R} (R \Sigma_0 v_{1R}) + \frac{\Sigma_0}{R} \frac{\partial v_{1\varphi}}{\partial \varphi}\] \[\nabla \cdot (\Sigma_1 \mathbf{v}_0) = \frac{1}{R} \frac{\partial}{\partial \varphi} (\Sigma_1 v_{0\varphi}) = \Omega \frac{\partial \Sigma_1}{\partial \varphi}\]のように計算されるため、(27)式は
\[\frac{\partial \Sigma_1}{\partial t} + \Omega \frac{\partial \Sigma_1}{\partial \varphi} + \frac{1}{R} \frac{\partial}{\partial R} (R \Sigma_0 v_{1R}) + \frac{\Sigma_0}{R} \frac{\partial v_{1\varphi}}{\partial \varphi} = 0 \tag{28}\]のように書き換えられます。 (15)式を思い出すと、これはさらに
\[-i(\omega -m \Omega) \Sigma_1 + \frac{1}{R} \frac{d}{dR} (R \Sigma_0 v_{1R}) + \frac{im \Sigma_0}{R} v_{1\varphi} = 0 \tag{29}\]のように整理されます。
渦巻き状の摂動の近似
\(v_{R, 1a}, v_{\varphi, 1a}, \Sigma_{1a}, h_{1a}, \Phi_{1a}\)の5つの未知変数に対し、これまでに私たちが導出できたのは(19), (20), (24), (29)の4式です。 よってこのままでは変数を決定することができません。 そこで
\[\Sigma_1 (R, \varphi, t) = H(R, t) e^{i(m\varphi + f(R, t))} \tag{30}\]のような密度場の摂動を考えましょう。 ここで\(f(R, t)\)は形状関数 (shape function)と呼ばれるもので
\[m\varphi + f(R, t) = (定数) \quad (\mathrm{mod} \ 2\pi) \tag{31}\]が、\(m\)本の渦状腕部分に対応します。 さらに
\[k(R, t) = \frac{\partial f (R, t)}{\partial R} \tag{32}\]は、動径方向の波数となります。 また\(k\)の符号は、その腕がリーディングなのかトレーリングなのかに対応します。 \(k>0\)ではトレーリングアームとなり、\(k<0\)ではリーディングアームとなります。 つまり(30)式は、渦状の密度ゆらぎを与えたことになります。 今は渦状腕構造について調べているため、この摂動を考えることに、特に不自然さはないはずです。 ではこれに対応する重力ポテンシャルを考えてみましょう。 しかしこれも一般に求めるのは難しいため
\[f(R, t) \approx f(R_0, t) + k(R_0, t) (R-R_0) \tag{33}\]のような近似を用い、さらに\(H(R, t)\)は\(R\)に対してゆっくり変化するものとします。 すなわち\(H(R, t) \approx H(R_0, t)\)のように、\(R_0\)の近傍だけで すると
\[\Sigma_1 \approx \Sigma_k e^{i(m\varphi + k(R-R_0))} \quad (\Sigma_k \equiv H(R_0 t) e^{if(R_0, t)}) \tag{34}\]のように書き換えることができます。 これは、この渦状の密度ゆらぎが平面波で近似できることを表しています。 この場合の重力ポテンシャルは、回転する平板での自己重力不安定性の部分で求めた形から
\[\Phi_1 = - \frac{2\pi G}{\vert k \vert} \Sigma_1 \tag{35}\]のようになります。
局所解析近似 (local analysis) またはWKB近似による分散関係式の導出
この近似だけでもまだ解析的に解くのが困難であるため、さらにもう1つの近似を考えます。 それは、この渦状腕がきつく巻いている(tightly wounding)を課すというものです。 すると\(\vert k R \vert \gg 1\)となることから、例えば(19)式においては
\[\frac{d}{dR} (\Phi_{1} + h_{1}) \gg \frac{\Phi_{1} + h_{1}}{R}\]のようになり、\((\Phi_{1}+h_{1})/R\)の項は無視できるようになります。 量子力学から、この近似はWKB近似とも呼ばれます。 この近似を適用すると、(19), (20)式は
\[v_{R, 1} \approx \frac{i(\omega - m\Omega)}{\Delta} \frac{d}{dR} (\Phi_1 + h_1) = -\frac{k(\omega - m\Omega)}{\Delta} (\Phi_1 + h_1) \tag{36}\] \[v_{\varphi, 1} \approx - \frac{2ikB}{\Delta} (\Phi_1 + h_1) \tag{37}\]のようになります。 (36), (37)式から、\(v_{R, 1}, v_{\varphi, 1}\)が同じオーダー程度であることもわかります。 よって(29)式は
\[\begin{align} &-i (\omega - m \Omega) \Sigma_1 + \frac{1}{R} \frac{d}{dR} (R \Sigma_0 v_{1, R}) = 0 \notag \\ & \Longrightarrow \ -i (\omega - m \Omega) \Sigma_1 + \frac{\Sigma_0 v_{1R}}{R} + ik\Sigma_0 v_{1, R} \approx -i (\omega - m \Omega) \Sigma_1 + ik\Sigma_0 v_{1, R} = 0 \notag \\ &\Longrightarrow \ -(\omega - m\Omega) \Sigma_1 + k \Sigma_0 v_{1, R} = 0 \tag{38} \end{align}\]のようになります。 (36), (38)式より
\[-(\omega -m\Omega) \Sigma_1 -k^2 \Sigma_0 \frac{\omega -m\Omega}{\Delta} (\Phi_1 + h_1) = 0\]ここに(24), (35)式を代入すると
\[\left\{ -(\omega -m\Omega) -k^2 \Sigma_0 \frac{\omega -m\Omega}{\Delta} \left( \frac{c_s^2}{\Sigma_0} - \frac{2\pi G}{\vert k\vert}\right) \right\} \Sigma_1 = 0\]任意の\(\Sigma_1\)においてこれが成り立つためには、\(\{\cdots \}=0\)となる必要があります。 以上より
\[-\Delta - c_s^2 k^2 - 2\pi G \Sigma_0 \vert k\vert = 0 \ \Longrightarrow \ (\omega - m\Omega)^2 = c_s^2 k^2 - 2\pi G \Sigma_0 \vert k \vert + \kappa^2 \tag{39}\]のような、分散関係式を得ます。 ここでトゥームレのQパラメータ\(Q = \frac{\kappa c_s}{\pi G \Sigma_0}\)を用いて右辺を整理すると
\[(\omega - m\Omega)^2 = c_s^2 \left( \vert k \vert - \frac{\pi G \Sigma_0}{c_s^2} \right)^2 - \frac{\pi^2 G^2 \Sigma_0^2}{c_s^2} + \kappa^2 = c_s^2 \left( \vert k \vert - \frac{\pi G \Sigma_0}{c_s^2} \right)^2 + \kappa^2 \left( 1 - \frac{1}{Q^2}\right) \tag{40}\]のようになります。 (40)式の右辺を横軸\(\vert k\vert\)のグラフで書くと、頂点の座標が\((\frac{\pi G \Sigma_0}{c_s^2}, \kappa^2(1-\frac{1}{Q^2}))\)である2次関数となります。 すると\(Q<1\)では\(1-\frac{1}{Q^2}<0\)となることから、\(\omega-m \Omega\)が複素数となり、密度波が不安定となる領域が存在するとわかります。
以降では安定に存在できる密度波を考察するため、\(Q \geq 1\)の場合のみについて解析を進めましょう。 (39)式は\(\vert k\vert\)の二次関数であるため、解の公式を用いて\(\vert k\vert\)を求めることができます。 すると
となります。 途中
\[\nu \equiv \frac{\omega - m\Omega}{\kappa} = \frac{m(\Omega_p-\Omega)}{\kappa} \tag{42}\]のように定義しました。 そして\(\Omega_p = \omega /m\)はパターン速度 (pattern speed)と呼ばれるもので、渦状腕の角速度を表します。 すなわち\(\nu\)は、銀河回転に乗った点が、渦状腕と出会う振動数を\(\kappa\)の単位に表したものです。 運動学的な密度波の部分で説明した通り、\(\nu = 0\)、すなわち\(\Omega_p = \Omega\)となる場所を共回転半径と呼びます。 そして特に\(m=2\)において、\(\nu = \pm 1\)のとき、すなわち\(\Omega_p = \Omega \pm \frac{\kappa}{2}\)をリンドブラッド共鳴点と呼びます。 この分散関係式を図示すると、下図のようになります。

ここでは\(Q=1.0, 1.05, 2.0\)の場合を描画しました。 (41)式を見ると、\(\pm\)から2つの分枝の存在がわかります。 \(+\)の方は、波数が大きい(波長が短い)ことから、short wave (略してS)と呼ばれます。 反対に\(-\)の方は、波数が小さい(波長が長い)ことから、long wave (略してL)と呼ばれます。 そしてTはトレーリング波を表し、この図ではST, LTの2つずつが描画されています。 (41)式の左辺は\(\vert k \vert\)であることから、本来は\(k<0\)の部分にも同様のグラフが描かれます。 \(k<0\)部分ではリーディング波となることから、その部分の波動をそれぞれLL, SLなどと呼びます。 \(\nu = 1\)の破線は外側リンドブラッド共鳴点を表します。
群速度と密度波の理解
群速度\(v_g\)から、先程の図をさらに理解しましょう。 (39)式の両辺を\(k\)で微分すると
\[2(\omega - m\Omega) \frac{\partial \omega}{\partial k} = \mathrm{sign} (k) ( 2c_s^2 \vert k \vert - 2 \pi G \Sigma_0 ) \ \Longrightarrow \ v_g = \mathrm{sign} (k) \frac{c_s^2 \vert k \vert -\pi G \Sigma_0}{\omega - m \Omega} \tag{43}\]のように計算することができます。 実はこのような計算をせずとも、先程の図から\(k\)と\(\nu (\omega)\)の関係、そして群速度の向きを見ることができます。 群速度が\(\omega\)を\(k\)で微分したものであることから、上図の\(\nu\)が最小となる部分で、群速度の符号(すなわち波のエネルギーの伝搬方向)が変わることがわかります。 例えば、\(Q=1.05\)のグラフを見てみましょう。 この場合、\(k/k_T=1.0, \nu=0.5\)の密度波は、その群速度が負であることから、渦巻銀河の内側に伝搬していきます。 それと同時に\(k\)の値を時々刻々と変化させ、\(k/k_T\sim 1.8, \nu \sim 0.3\)のあたりで最小となり、そこからは群速度が正となります。 すなわち、先程の密度波はそこから渦巻銀河の内側に進むことができず、ある半径で渦巻銀河の外側へと伝播していくことになるのです。 \(\nu = 0\)が共回転半径であることから、このトレーリング波は(\(Q=1\)の場合を除いて)共回転半径まで到達することなく、外側へと反射されます。 この反射をQバリアと呼びます。 最初はSTだった密度波が、LTになって外側に反射されていることもわかります。 以上の議論から、密度波が存在できる領域が、\(Q\)に依存して制限されることがわかりました。
分散関係式の物理的意味
\(k \gg 1\)のとき、(39)式の分散関係式は
\[(\omega - m\Omega)^2 \approx c_s^2 k^2\]のようになり、右辺が負になるような領域は存在しません。 このことから、音波による密度ゆらぎをならす力が、系を安定化させることがわかります。 逆に、\(k \ll 1\)の場合を考えましょう。 すると
\[(\omega - m \Omega)^2 \approx \kappa^2\]のように、右辺が負になることがありません。 この場合は、エピサイクリック運動が密度ゆらぎをならすことで系を安定化させ、密度波が永続的に存在できることを意味します。 この間の領域で系が不安定となり、密度波が存在できないことがわかります。
この分散関係式を求める仮定は正しい?
実際の渦巻銀河の渦状腕は、恒星が集団として集まることで形成され、より明るく見えているのでした。 しかしここまでの議論では、私たちは恒星系を流体近似し、まるでガス円盤であるかのように扱ってきました。 恒星系をより厳密に扱うならば、それら粒子を記述するための無衝突ボルツマン方程式を用いる方が、より厳密なはずです。 ここでは詳細は省略しますが、無衝突ボルツマン方程式から出発して導出される分散関係式は、(39)式とは異なります。 よって先程の図も異なる様子を示します。 先程の密度波はQバリアで反射されたのち、\(R \rightarrow \infty\)に飛び去ると考えられますが、無衝突ボルツマン方程式から得られたものは、外側リンドブラッド共鳴点に漸近するようなものとなります。 つまりこれは、外側リンドブラッド共鳴点で密度波が減衰することを表しています。 言い換えれば、密度波が存在できる範囲は共回転半径より外側のQバリアから、外側リンドブラッド共鳴点までの間の領域に限られるということがわかります。
(無衝突ボルツマン方程式を用いた恒星円盤における分散関係式の導出は、元気があるときに行う予定です。 今しばらくお待ちください。)
この理論は数値実験と一致するか?
ここまでで、この密度波は確かに渦状腕状の波動を形成することができるとわかりました。 しかし先程述べたとおり、外側リンドブラッド共鳴点で密度波が減衰することから、この波動を定常的に維持するには、別の物理機構が必要となることがわかります。 また密度波理論では、波数\(k\)の正負によってトレーリングかリーディングかが決定されますが、実際の銀河ではどのようにこれらが決定されるかはわかりません。 そこで、きつく巻いた近似やゆらぎの線形性や定常性を仮定しない数値シミュレーションが、盛んに行われてきました。 代表的な研究として、Fujii et al. (2011)があります。 この研究では\(3 \times 10^6\)個や\(3 \times 10^7\)個の粒子を用い、円盤銀河の重力多体計算を行いました。 すると、定常的な密度波による定常的な渦状腕ではなく、非定常な渦状腕の振る舞いが現れたのです。 円盤中に自然に発生した渦状腕は、途中で千切られたり合体したりするものの、円盤には常に渦状腕構造が見られることがわかりました。
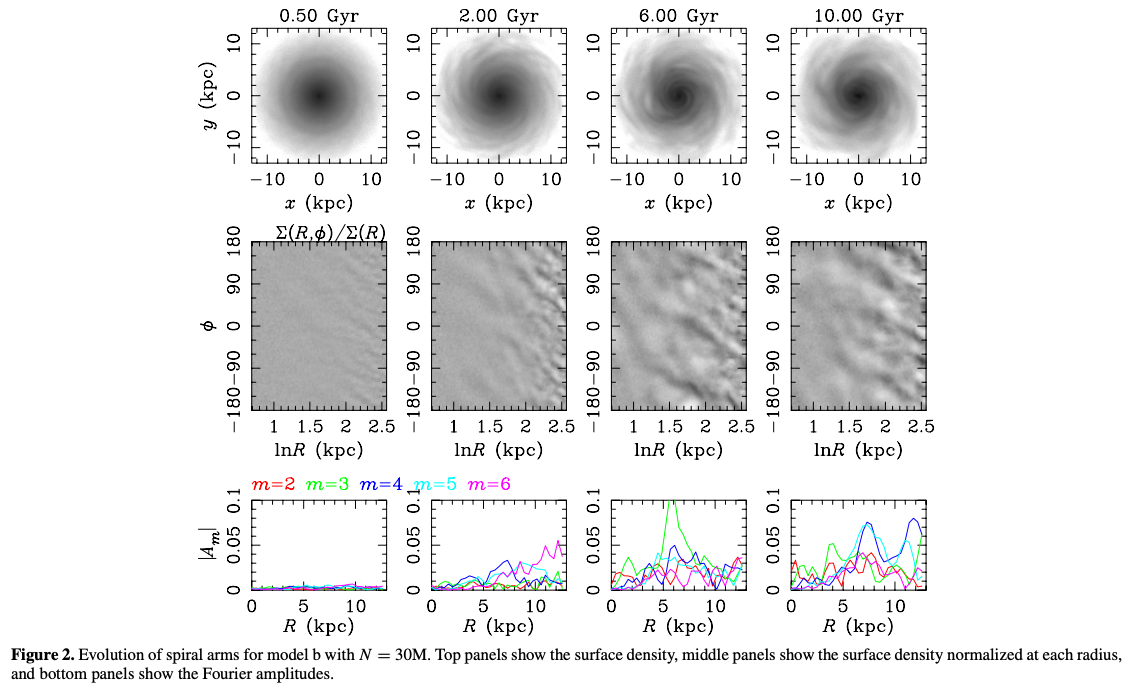
上図の上段は円盤銀河を上から眺めた様子、中断は横軸と縦軸にそれぞれ半径\(\ln (R)\)と方位角方向\(\varphi\)を取ったときの密度、そして下段はある半径での腕の本数\(m\)の振幅をフーリエ変換から求めたもの、を図示しています。 これらの図からもわかるように、渦状腕はその長さや太さ、そして腕の本数すらも時々刻々と変化させながら、10Gyrという宇宙年齢にも及ぶ時間にわたって渦状腕構造を維持することがわかります。 この研究では円盤を構成する恒星質量とバルジの恒星質量の比や、初期の\(Q\)の値を様々に変えた場合についても計算を行い、それらが与える影響についても調査しています。 より詳しくは原論文をぜひご覧ください。
参考文献
[1] Fujii et al., 2011, “The Dynamics of Spiral Arms in Pure Stellar Disks”
[2] Binney & Tremaine, “Galactic Dynamics: Second Edition”
[3] 祖父江義明, 有本信雄, 家正則, “シリーズ現代の天文学5 銀河II”
[4] 福江純, 和田圭一, 梅村雅之, “宇宙流体力学の基礎”
[5] 馬場淳一, “渦巻銀河ダイナミクス理論の進展と天の川銀河”