Table of contents
電磁多重極放射
ジェフィメンコ方程式から、任意の電荷分布・電流分布による電磁放射は以下のように書けました。
\[\mathbf{E} = \iiint \frac{1}{c^2 R} \left( \left[ \frac{\partial \mathbf{j}}{\partial t}\right] \times \mathbf{n} \right) \times \mathbf{n}dV \tag{1}\] \[\mathbf{B} = \iiint \frac{1}{c^2R} \left[ \frac{\partial \mathbf{j}}{\partial t} \right] \times \mathbf{n} dV \tag{2}\]以下ではこれを多重極展開することで、双極子放射成分と四重極子放射成分を導出してみましょう。
電気双極子放射
まずは電荷・電流分布が存在する位置\(\mathbf{r}_0\)から観測者のいる位置\(\mathbf{r}\)までの距離\(R\)において、\(\vert \mathbf{r}_0 \vert \ll \vert \mathbf{r} \vert\)としてテイラー展開しましょう。これは座標原点近傍にのみ電荷・電流分布が存在していることに対応します。ここで\(\mathbf{r} = (x, y, z), \mathbf{r}_0 = (x_0, y_0, z_0)\)とすると
\[\begin{aligned} R &= |\mathbf{r} - \mathbf{r}_0| = \sqrt{x^2 \left( 1- \frac{x_0}{x} \right) + y^2 \left( 1- \frac{y_0}{y} \right) + z^2 \left( 1- \frac{z_0}{z} \right)} \\ &\simeq \sqrt{x^2 \left( 1-\frac{2x_0}{x}\right) + y^2 \left( 1-\frac{2y_0}{y}\right) + z^2 \left( 1-\frac{2z_0}{z}\right)} = \sqrt{r^2 - 2 \mathbf{r} \cdot \mathbf{r}_0} = r \sqrt{1-2\frac{\mathbf{r} \cdot \mathbf{r}_0}{r^2}} \\ &\simeq r \left( 1 - \frac{\mathbf{r} \cdot \mathbf{r}_0}{r^2} \right) \end{aligned}\]これより、遅延時刻は
\[t_\mathrm{ret} = t-\frac{R}{c} \simeq t-\frac{r}{c} + \frac{\mathbf{r} \cdot \mathbf{r}_0}{cr} = t_0 + \frac{\mathbf{r}\cdot \mathbf{r}_0}{cr} \tag{3}\]のように近似されます。\(t_0\)は原点から放射があったとした場合の遅延時刻です。すると同様に遅延時刻における電流密度ベクトルは
\[[ \mathbf{j}] = \mathbf{j} (\mathbf{r}_0, t_\mathrm{ret}) = \mathbf{j} (\mathbf{r}_0, t_0 + \frac{\mathbf{r} \cdot \mathbf{r}_0}{cr}) \simeq \mathbf{j} (\mathbf{r}_0, t_0) + \frac{\mathbf{r} \cdot \mathbf{r}_0}{cr} \left. \frac{\partial \mathbf{j}}{\partial t} \right|_{t=t_0} = [\mathbf{j}]_0 + \frac{\mathbf{r} \cdot \mathbf{r}_0}{cr} \left[ \frac{\partial \mathbf{j}}{\partial t}\right]_0 \tag{4}\]のように書けます。ここで\([\cdots ]_0\)は遅延時刻\(t_0\)における量を表す記号です。それでは双極子放射から計算していきましょう。
この系における電気双極子モーメントは
です。この両辺を時間微分すると
\[\frac{\partial \mathbf{p}}{\partial t} = \iiint dV \mathbf{r}_0 \left. \frac{\partial \rho}{\partial t} \right|_{t=t_0} = - \iiint dV \mathbf{r}_0 (\nabla_{\mathbf{r}_0} \cdot \mathbf{j} )\]となります。途中、電荷分布と電流分布に対する連続の式を用いました。右辺の積分は、部分積分などを用いて具体的に計算すると
\[\iiiint dV \frac{\partial j_x}{\partial x_0} x_0 = \iiint dx_0 dy_0 dz_0 \frac{\partial j_x}{\partial x_0} x_0 = \iint dy_0 dz_0 \left( [j_x x_0]_{-\infty}^\infty - \int_{-\infty}^\infty j_x dx_0 \right) = - \iiint dx_0 dy_0 dz_0 j_x\] \[\iiiint dV \frac{\partial j_y}{\partial y_0} x_0 = \iiint dx_0 dy_0 dz_0 \frac{\partial j_y}{\partial y_0} x_0 = \iint dx_0 dz_0 x_0 [j_y ]_{-\infty}^\infty = 0\]などとなります。途中、無限遠での表面積分は0であることを使いました。これらより
\[\frac{\partial \mathbf{p}}{\partial t} = \iiint \mathbf{j}(\mathbf{r}_0, t_0) dV \tag{6}\]となります。(1), (4), (6)式より、電流密度ベクトルを展開したときの0次成分から出る電磁放射は
\[\mathbf{E} = \frac{1}{c^2 R} \left( \left[ \frac{\partial^2 \mathbf{p}}{\partial t^2}\right]_0 \times \mathbf{n} \right) \times \mathbf{n} \tag{7}\]となります。最後の計算式では\(\mathbf{n} = \frac{\mathbf{r} - \mathbf{r}_0}{\vert \mathbf{r} - \mathbf{r}_0 \vert} \simeq \frac{\mathbf{r}}{r}\)として、積分の外に出して計算を行いました。
磁気双極子成分と電気四重極放射
(1), (2)式より\(\mathbf{E} = \mathbf{B} \times \mathbf{n}\)より、以下では磁場を変形することにしましょう。(4)式の\(\left[ \frac{\partial \mathbf{j}}{\partial t}\right]\)の項による電磁放射は
\[\mathbf{B} = \frac{1}{c^2 R} \iiint dV \left(\frac{\mathbf{n} \cdot \mathbf{r}_0}{c} \left[ \frac{\partial^2 \mathbf{j}}{\partial t^2} \right]_0 \right) \times \mathbf{n}\]です。途中\(\mathbf{r} / R = \mathbf{n}\)としました。\((\mathbf{n} \cdot \mathbf{r}_0) \left[ \frac{\partial \mathbf{j}}{\partial t}\right]_0 = \frac{1}{2} (\mathbf{n} \cdot \mathbf{r}_0) \left[ \frac{\partial \mathbf{j}}{\partial t}\right]_0 + \frac{1}{2} (\mathbf{n} \cdot \mathbf{r}_0) \left[ \frac{\partial \mathbf{j}}{\partial t}\right]_0\)のように2つに分け、さらに\(\frac{1}{2} \left( \left[ \frac{\partial^2 \mathrm{j}}{\partial t^2}\right] \cdot \mathrm{n} \right) \mathrm{r}_0 - \frac{1}{2} \left( \left[ \frac{\partial^2 \mathrm{j}}{\partial t^2}\right] \cdot \mathrm{n} \right) \mathrm{r}_0\)を追加すると
\[\begin{align} \mathbf{B} &= \frac{1}{c^3 R} \iiint \frac{1}{2} \left\{ (\mathbf{n} \cdot \mathbf{r}_0) \left[ \frac{\partial^2 \mathbf{j}}{\partial t^2} \right] - \left( \left[ \frac{\partial^2 \mathbf{j}}{\partial t^2}\right] \cdot \mathbf{n}\right) \mathbf{r}_0\right\} \times \mathbf{n} dV \notag \\ & \qquad + \frac{1}{c^3 R} \iiint \frac{1}{2} \left\{ (\mathbf{n} \cdot \mathbf{r}_0) \left[ \frac{\partial^2 \mathbf{j}}{\partial t^2} \right] + \left( \left[ \frac{\partial^2 \mathbf{j}}{\partial t^2}\right] \cdot \mathbf{n}\right) \mathbf{r}_0\right\} \times \mathbf{n} dV \tag{8} \end{align}\]第一項を\(\mathbf{B}_\mathrm{M1}\)、第二項を\(\mathbf{B}_\mathrm{E2}\)のように書きます。ベクトル恒等式より
\[\left( \mathbf{r}_0 \times \left[ \frac{\partial^2 \mathbf{j}}{\partial t^2}\right]_0\right) \times \mathbf{n} = (\mathbf{n} \cdot \mathbf{r}_0) \left[ \frac{\partial^2 \mathbf{j}}{\partial t^2}\right]_0 - \left( \left[ \frac{\partial^2 \mathbf{j}}{\partial t^2} \right] \cdot \mathbf{n}\right) \mathbf{r}_0\]です。さらに磁気双極子
\[\mathbf{m} = \frac{1}{2c} \iiint \mathbf{r}_0 \times \mathbf{j} dV \tag{9}\]を用いれば
\[\mathbf{B}_\mathrm{M1} = \frac{1}{c^2R} \left( \left[ \frac{\partial^2 \mathbf{m}}{\partial t^2} \right]_0 \times \mathbf{n} \right) \times \mathbf{n} \tag{10}\]のようになります。よって\(\mathbf{B}_\mathrm{M1}\)は磁気双極子の時間変化により電磁放射成分であるとわかります。
続いて\(\mathbf{B}_\mathrm{E2}\)を計算しましょう。そのために以下の計算を行います。
ベクトルを\(\mathbf{a} = a_i \mathbf{e}_i = (\mathbf{a} \cdot \mathbf{e}_i) \mathbf{e}_i\)のように、成分ごとに分割して書き下しました。さらに\(\mathbf{e}_i\)は\(x, y, z\)方向の単位ベクトルです。この単位ベクトルは、例えば
\[\mathbf{e}_x = \nabla_0 x_0 = (\frac{\partial x_0}{\partial x_0},\frac{\partial x_0}{\partial y_0},\frac{\partial x_0}{\partial z_0}) = (1, 0, 0)\]のように計算できるので、\(\mathbf{e}_i = \nabla_0 r_{0, i}\)のように書くことができます。よって
\[\begin{aligned} \iiint (\mathbf{n} \cdot \mathbf{r}_0) \left[ \frac{\partial^2 \mathbf{j}}{\partial t^2}\right]_0 dV &= \left\{ \iiint (\mathbf{n}\cdot \mathbf{r}_0) \left[ \frac{\partial^2 \mathbf{j}}{\partial t^2}\right]_0 \cdot (\nabla r_{0, i}) \right\} \mathbf{e}_i \\ &= \left( \iiint \nabla \cdot \left\{ (\mathbf{n}\cdot \mathbf{r}_0) r_{0, i} \left[ \frac{\partial^2 \mathbf{j}}{\partial t^2}\right]_0\right\} dV - \iiint r_{0, i} \nabla \cdot \left\{ (\mathbf{n} \cdot \mathbf{r}_0) \left[ \frac{\partial^2 \mathbf{j}}{\partial t^2}\right]_0\right\} dV\right) \mathbf{e}_i \\ &\underbrace{=}_{表面積分は0} - \left( \iiint r_{0, i} \left\{ (\mathbf{n} \cdot \mathbf{r}_0) \left( \nabla \cdot \left[ \frac{\partial^2 \mathbf{j}}{\partial t^2}\right]_0\right) + \left[ \frac{\partial^2\mathbf{j}}{\partial t^2} \right]_0 \cdot \nabla (\mathbf{n} \cdot \mathbf{r}_0)\right\} dV \right) \mathbf{e}_i \end{aligned}\]電荷分布と電流分布に成り立つ連続の式より
\[\nabla \cdot \left[ \frac{\partial^2 \mathbf{j}}{\partial t^2}\right] = - \left[ \frac{\partial^3 \rho}{\partial t^3}\right]\]です。さらに\(\nabla_0 (\mathbf{n} \cdot \mathbf{r}_0) = \mathbf{n}\)より
\[\begin{aligned} \iiint (\mathbf{n} \cdot \mathbf{r}_0) \left[ \frac{\partial^2 \mathbf{j}}{\partial t^2}\right]_0 dV &= \left\{ \iiint r_{0, i} \left[\frac{\partial^3 \rho}{\partial t^3} \right]_0 (\mathbf{n} \cdot \mathbf{r}_0) dV \right\} \mathbf{e}_i - \left\{ \iiint \left(\mathbf{n} \cdot \left[ \frac{\partial^2 \mathbf{j}}{\partial t^2}\right]_0 \right) r_{0, i} dV \right\} \mathbf{e}_i \\ &= \iiint \left[\frac{\partial^3 \rho}{\partial t^3} \right]_0 (\mathbf{n} \cdot \mathbf{r}_0) \mathbf{r}_0 dV - \iiint \left( \mathbf{n} \cdot \left[ \frac{\partial^2 \mathbf{j}}{\partial t^2}\right]_0 \right) \mathbf{r}_0 dV \end{aligned}\]となります。(8)式の第二項\(\mathbf{B}_\mathrm{E2}\)見比べることで
\[\mathbf{B}_\mathrm{E2} = \frac{1}{2c^3 R} \left\{ \iiint (\mathbf{n} \cdot \mathbf{r}_0) \left[ \frac{\partial^3 \rho}{\partial t^3}\right]_0 \mathbf{r}_0 dV \right\} \times \mathbf{n}\]ここで\(\mathbf{n} = \frac{r_k}{r} \mathbf{e}_k, \mathbf{r}_0 = r_{0, \ell} \mathbf{e}_\ell\)のように書けば
\[\mathbf{B}_\mathrm{E2} = \frac{1}{2c^3 R} \left\{ \iiint \frac{r_k r_{0, k}}{r} \left[ \frac{\partial^3 \rho}{\partial t^3}\right]_0 r_{0, \ell} \mathbf{e}_\ell dV \right\} \times \mathbf{n}\]となります。さらに電気四重極モーメントが
\[Q_{k\ell} = \iiint r_{0, k} r_{0, \ell} \rho dV \tag{11}\]のように書かれるので、電流密度ベクトルを展開した時の1次成分から出る電磁放射は
\[\mathbf{B}_\mathrm{E2} = \frac{1}{2c^3 R} \left( \frac{R_k}{R} \left[ \frac{\partial^3 Q_{k\ell}}{\partial t^3}\right]_0\mathbf{e}_\ell \right) \times \mathbf{n} \tag{12}\]と求まります。最後に\(R \simeq r\)としました。
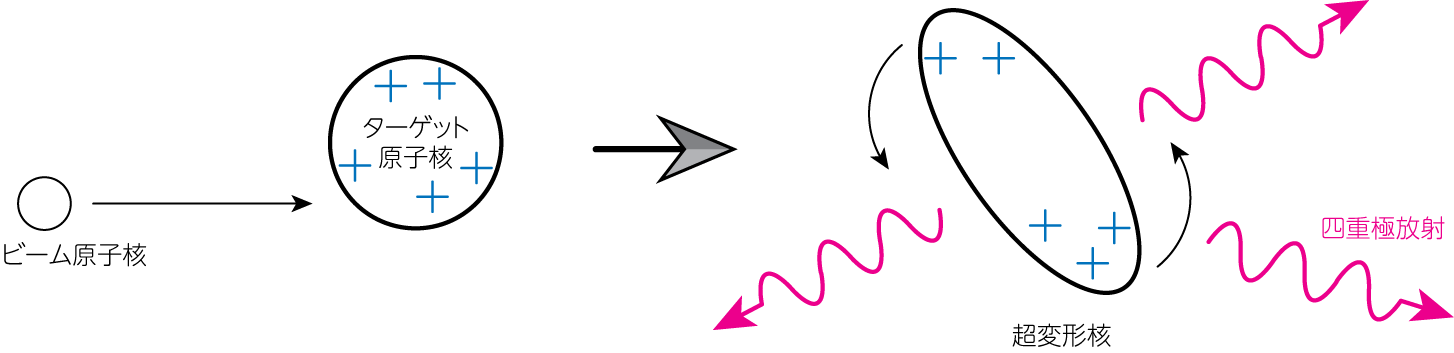
応用: 超変形核
ターゲットとする原子核にビーム原子核をある角度で撃ち込むと、ターゲット原子核と核融合を起こすと同時に角運動量を獲得し、高速回転を始めます。これにより超変形核となります。この場合、原子核の四重極モーメントが0ではなくなり、(12)式で表されるような四重極モーメントの時間変化による電磁放射が生まれます。逆に、この超変形核からの電磁場を検出器で観測し(12)式を解けば、超変形核の四重極モーメントの分布が得られます。
参考文献
- Haras, 2007, “Can Maxwell’s equations be obtained from the continuity equation?”
- Souza et al., 2009, “Multipole radiation fields from the Jefimenko equation for the magnetic field and the Panofsky-Phillips equation for the electric field”
- 中村哲, 須藤彰三, “電磁気学”
- 東北大学原子核物理グループ
- 不安定核の集団現象に対する微視的アプローチ