Table of contents
RMを用いた銀河団磁場の推定
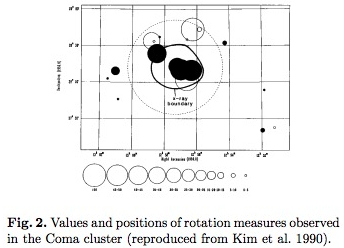
“Filled and unfilled circles represent positive and negative RMs, respectively. The sizes of circles are proportional to the absolute values of RMs.”
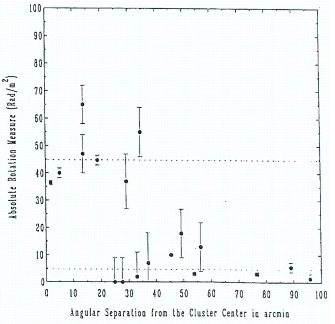
“The RM distribution against the angular separation from the cluster center.”
“These figures show the excess RMs of ~40 rad [tex: {\rm m}^{-2}] for the sources seen through the cluster.”
図はかみのけ座銀河団という近傍の巨大銀河団の背景にある天体のRotation Measureの測定結果です。以下では、かみのけ座銀河団は我々から距離100Mpcに存在するとし、半径\(L=1\)Mpcの球内が一様に密度\(n_e=10^{-3} {\rm cm}^{-3}\), 温度\(k_B T = 10\)keVの電子・陽子プラズマで満たされた天体とします。
かみのけ座銀河団に磁場が存在することの証拠
半径\(L\)が1Mpc, 距離が100Mpcにあるので、この天体を見込む角度は
\[\theta = \frac{1{\rm Mpc}}{100{\rm Mpc}} [ {\rm rad}] = 10^{-2} \frac{180}{\pi} 60 [ {\rm arcmin}] \sim 36 [ {\rm arcmin}]\]となります。fig. 2からおよそ35arcminまでのRMの値の大きさが、その外側のRMの値の大きさに比べて有意に大きいことがわかります。よってこれはかみのけ座銀河団があることによりRMが増加していることを意味し、かみのけ座銀河団に磁場が存在していることを示しています。
磁場が一様分布の場合
ここではかみのけ座銀河団内に磁場が一様に分布しているとして、中心部での磁場の大きさを見積もってみましょう。RMは
\[{\rm RM} = 0.812 \int_0^{d/1{\rm pc}} \frac{B_{\parallel}}{1{\rm \mu G}} \frac{n_e}{1 {\rm cm}^{-3}} ds \ [ {\rm rad} {\rm m}^{-2} ]\]で与えられます。今、磁場が球内に一様に分布しているとの仮定から
\[{\rm RM} = 0.8 \frac{B_\parallel}{1{\rm \mu G}} \frac{n_e}{1 {\rm cm}^{-3}} \frac{2\pi L}{1 {\rm pc}}\]fig. 1から、計算を簡単化するために\({\rm RM} \sim 40 {\rm rad} {\rm m}^{-2}\)とすると
\[B_\parallel \sim 8 \times 10^{-3} [\mu {\rm G} ]\]とわかります。
磁場が一様分布でない場合
磁場のcoherent lengthが\(\ell = 10\)kpcであるとします。すなわち、\(\ell\)ごとに磁場の向きが視線方向に対して平行・反平行とランダムに変わるものします。図に示したRMはこの状況で複数の視線方向を観測したときの分散値であるとして、銀河団中心付近の磁場の強度を見積もってみましょう。
そのためにはランダムウォークを考えます。ランダムウォークの回数\(N\)ののちに銀河団を通過してきたと考えると、分散との関係式より
の関係があります。磁場の向きが反転する回数は大雑把に\(N \simeq R/\ell\)とすると、\(\sigma \simeq \sqrt{2\pi L \ell}\)より
\[40 [ {\rm rad m}^{-2} ] = 0.8 \frac{B_\parallel}{1 {\rm \mu G}} \frac{n_e}{1 {\rm cm}^{-3}} \frac{\sigma}{1{\rm pc}} \ \Longrightarrow \ B_\parallel \sim 0.2 [ {\mu G} ]\]と求まります。