Table of contents
回転する平板での自己重力不安定性
宇宙には銀河円盤や原始惑星系円盤など、様々な回転円盤が存在します。ここでは回転がある場合の自己重力不安定性を調べ、回転がジーンズ不安定性に与える影響を調べましょう。
問題設定
今度は\(z=0\)平面にのみガスが分布し、この平板が角速度\(\boldsymbol{\Omega} = \Omega \mathbf{e}_z\)で回転しているとしましょう。面密度や速度場をそれぞれ
\[\Sigma (x, y) = \int \rho(x, y, z) dz, \quad \mathbf{v} (x, y) = \frac{1}{\Sigma} \int \rho(x, y, z) \mathbf{v} (x, y, z) dz \tag{1}\]のように定義します。以下ではこの回転に乗った系、すなわち回転座標系で物事を考えます。
初期状態では流体は静止しており、面密度も一様であるとします。すなわち\(\Sigma = \Sigma_0 (定数), P = P_0 (定数), \mathbf{v} = \mathbf{v}_0 = \mathbf{0}, \Phi = \Phi_0\)とすると、連続の式は
そして運動量保存則を表す式は、コリオリ力と遠心力を考慮して
\[\begin{align} \frac{\partial }{\partial t} (\Sigma_0 \mathbf{v}_0) + \nabla \cdot (\Sigma_0 \mathbf{v}_0 \mathbf{v}_0) &= - \nabla P_0 - \Sigma \nabla \Phi_0 - 2 \Sigma_0 \boldsymbol{\Omega} \times \mathbf{v}_0 + \Sigma_0 \Omega^2 (x \mathbf{e}_x + y \mathbf{e}_y) \notag \\ &= - \Sigma_0 \nabla \Phi_0 + \Sigma_0 \Omega^2 (x \mathbf{e}_x + y \mathbf{e}_y) = \mathbf{0} \tag{3} \end{align}\]となります。最後に、重力のポアソン方程式は
\[\nabla^2 \Phi_0 = 4\pi G \Sigma_0 \delta(z) \tag{4}\](18)式を微小区間\([-\epsilon, \epsilon]\)で積分することで、\(\Phi_0\)を求めましょう。
\[\frac{\partial \Phi_0}{\partial z}(\epsilon) - \frac{\partial \Phi_0}{\partial z}(-\epsilon) = 2\frac{\partial \Phi_0}{\partial z} (\epsilon) = 4\pi G \Sigma_0\]途中、\(z=0\)を挟んで対称な系であることから\(\partial \Phi_0 / \partial z(-\epsilon) = - \partial \Phi_0 / \partial z(\epsilon)\)を用いました。これをさらに\(z\)方向に積分すると
\[\Phi_0(x, y, z) = 2\pi G \Sigma_0 |z| + (x, y の関数) \tag{5}\]のように求まります。\(\Phi_0\)は(17)式も満たす必要があるため、最も簡単な形として
\[\Phi_0 (x, y, z) = 2\pi G \Sigma_0 |z| + \frac{\Omega^2}{2} (x^2 + y^2) \tag{6}\]としておきましょう。
基礎方程式の線形化
ここに微小な摂動が加わり、物理量がそれぞれ
\[\Sigma = \Sigma_0 + \Sigma_1, \quad P = P_0 + P_1, \quad \mathbf{v} = \mathbf{v}_0 + \mathbf{v}_1 = \mathbf{v}_1, \quad \Phi = \Phi_0 + \Phi_1\]のように変化したとしましょう。先程のジーンズ不安定性の時と同様に、この摂動が断熱的に起こっているとすると
\[P_1 = C_s^2 \Sigma_1 \tag{7}\]のように書けます。音速\(C_s\)は無摂動状態での音速なので、時間に依存しない定数です。これらより、連続の式は
\[\frac{\partial }{\partial t} (\Sigma_0 + \Sigma_1) + \nabla \cdot \{ (\Sigma_0 + \Sigma_1) \mathbf{v}_1\} \underbrace{=}_{(2)} \frac{\partial \Sigma_1}{\partial t} + \nabla \cdot (\Sigma_0 \mathbf{v}_1) \underbrace{=}_{\Sigma_0は定数} \frac{\partial \Sigma_1}{\partial t} + \Sigma_0 \nabla \cdot \mathbf{v}_1 = 0 \tag{8}\]となります。次に運動量保存の式は
\[\begin{aligned} &\frac{\partial }{\partial t} (\Sigma_0 + \Sigma_1) + \nabla \cdot \{ (\Sigma_0 + \Sigma_1) \mathbf{v}_1 \mathbf{v}_1\} \underbrace{=}_{(2)} \Sigma_0 \frac{\partial \mathbf{v}_1}{\partial t} \\ &= - \nabla (P_0 + P_1) - (\Sigma_0 + \Sigma_1) \nabla (\Phi_0 + \Phi_1) - 2 (\Sigma_0 + \Sigma_1) \boldsymbol{\Omega} \times \mathbf{v}_1 + (\Sigma_0 + \Sigma_1) \Omega^2 (x \mathbf{e}_x + y \mathbf{e}_y) \\ &= - \nabla \overbrace{P_1}^{(7)} \underbrace{- (\Sigma_0 + \Sigma_1) \nabla \Phi_0 + (\Sigma_0 + \Sigma_1) \Omega^2 (x \mathbf{e}_x + y \mathbf{e}_y)}_{(3)より\mathbf{0}} - \Sigma_0 \nabla \Phi_1 - 2 \Sigma_0 \boldsymbol{\Omega} \times \mathbf{v}_1 \end{aligned}\]のようになります。整理すると
\[\Sigma_0 \frac{\partial \mathbf{v}_1}{\partial t} = - C_s^2 \nabla \Sigma_1 - \Sigma_0 \nabla \Phi_1 - 2 \Sigma_0 \boldsymbol{\Omega} \times \mathbf{v}_1 \tag{9}\]最後にポアソン方程式は
\[\nabla^2 (\Phi_0 + \Phi_1) = 4\pi G (\Sigma_0 + \Sigma_1) \delta(z) \ \Longrightarrow \ \nabla^2 \Phi_1 = 4 \pi G \Sigma_1 \delta(z) \tag{10}\]のようになります。
分散関係式の導出
摂動により加わった微少量のフーリエ成分に着目するため
\[\mathbf{v}_1 = \delta \mathbf{v} e^{i(\omega t - \mathbf{k} \cdot \mathbf{x})}, \quad \Sigma_1 = \delta \Sigma e^{i(\omega t - \mathbf{k} \cdot \mathbf{x})}, \quad \Phi_1 = \delta \Phi e^{i(\omega t - \mathbf{k} \cdot \mathbf{x}) - |kz|} \tag{11}\]とします。ここで\(\delta \mathbf{v} = (\delta v_x, \delta v_y, 0)\)のように、2次元平面内での運動のみを考えます。\(\delta \Phi_1\)はポテンシャルなので、\(z \rightarrow 0\)で摂動の効果が0となるようにしています。(10)式の両辺を\(z\)方向に微小区間\([-\epsilon, \epsilon]\)で積分し、\(\epsilon \rightarrow 0\)の極限を取りましょう。
\[\lim_{\epsilon \rightarrow 0} \left\{ \int_{0-\epsilon}^{0+\epsilon} \left(\frac{\partial^2 \Phi_1}{\partial x^2} + \frac{\partial^2 \Phi_1}{\partial y^2}\right) dz + \int_{0-\epsilon}^{0+\epsilon} \frac{\partial^2 \Phi_1}{\partial z^2} dz \right\} = 4\pi G \Sigma_1\]左辺第一項は\(z\)に関して連続な関数なので、\(\epsilon \rightarrow 0\)の極限では0として大丈夫でしょう。第二項は
\[\lim_{\epsilon \rightarrow 0} \int_{0-\epsilon}^{0+\epsilon} \frac{\partial^2 \Phi_1}{\partial z^2} dz = \lim_{\epsilon \rightarrow 0} \left( \frac{\partial \Phi_1}{\partial z}(\epsilon) - \frac{\partial \Phi_1}{\partial z}(-\epsilon) \right) \underbrace{=}_{(11)} - 2 |k| \Phi_1\]のようになります。よって
\[\Phi_1 = - \frac{2\pi G}{|k|} \Sigma_1 \tag{12}\]のように計算されます。以降の計算では簡単のため、波数ベクトルを\(\mathbf{k} = (k_x, 0, 0)\)として計算を行いましょう。(8)式より
\[i\omega \Sigma_1 + \Sigma_0 (-i \mathbf{k}) \cdot \mathbf{v}_1 = 0 \ \Longrightarrow \ \omega\delta \Sigma - \Sigma_0 k_x \delta v_x = 0 \tag{13}\](9)式から
\[\Sigma_0 i \omega \mathbf{v}_1 = - C_s^2 (-i \mathbf{k}) \Sigma_1 - \Sigma_0 \nabla \Phi_1 - 2\Sigma_0 \Omega \mathbf{e}_z \times \mathbf{v}_1 = i C_s^2 \Sigma_1 \mathbf{k} + \Sigma_0 \frac{2\pi G}{|k|} (-i \mathbf{k}) \Sigma_1 - 2\Sigma_0 \Omega \mathbf{e}_z \times \mathbf{v}_1\]これをベクトルの形をあらわに書くと
\[i \omega \left( \begin{array}{c} \delta v_x \\ \delta v_y \end{array} \right) + i \left( - \frac{C_s^2}{\Sigma_0} + \frac{2\pi G}{|k|} \right) \left( \begin{array}{c} k_x \\ 0 \end{array} \right) \delta \Sigma - 2 \Omega \left( \begin{array}{c} - \delta v_y \\ \delta v_x \end{array}\right) = \mathbf{0}\]2つをまとめて
\[\left( \begin{array}{ccc} \omega & - \Sigma_0 k_x & 0 \\ i \left( - \frac{C_s^2}{\Sigma_0} + \frac{2\pi G}{|k|} \right) k_x & i\omega & 2\Omega \\ 0 & - 2\Omega & i\omega \end{array} \right) \left( \begin{array}{c} \delta \Sigma \\ \delta v_x \\ \delta v_y \end{array}\right) = \mathbf{0} \tag{14}\]のようになります。この固有値方程式を解けば良いことがわかります。\((\delta \Sigma, \delta v_x, \delta v_y) = \mathbf{0}\)という自明な解以外の解を探すには、係数行列の逆行列が存在しなければ良いでしょう。よって係数行列の行列式を計算すると
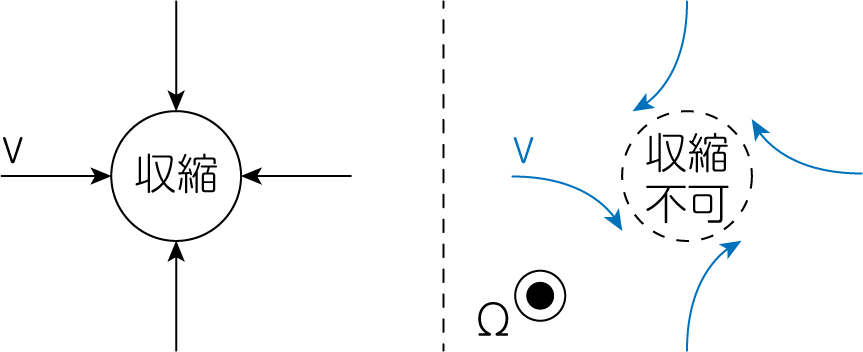
\[\begin{align} &\omega (-\omega^2 + 4\Omega^2) + \Sigma_0 k_x \left\{ i \left( - \frac{C_s^2}{\Sigma_0} + \frac{2\pi G}{|k|} \right) k_x i \omega - 0\right\} = 0 \notag \\ &\Longrightarrow \ \omega^2 = k_x^2 C_s^2 + (2\Omega)^2 - 2\pi G \Sigma_0 |k| \tag{15} \end{align}\]という分散関係式を得ます。途中\(k_x^2 =\vert k \vert^2\)としました。回転がない場合に比べて、回転は\((2\Omega)^2\)の項を生じ、安定化させる働きをしていることがわかります。それは回転によるコリオリ力によって、ガスが一箇所に集中しようとするのを妨げるためです(下図の右パネル)。
以下では\(k_x>0\)のみを考えましょう。このときに\(\omega^2 < 0\)、すなわち不安定となる波数が存在しないための条件を考えます。そのためには(15)式を
\[\omega^2 = C_s^2 \left( k_x - \frac{\pi G \Sigma_0}{C_s^2} \right)^2 - \frac{\pi^2 G^2 \Sigma_0^2}{C_s^2} + (2\Omega)^2\]のように変形したときに、\(k_x\)の2次関数の最小値が0より大きければ良いでしょう。よって
\[- \frac{\pi^2 G^2 \Sigma_0^2}{C_s^2} + (2\Omega)^2 > 0 \ \Longrightarrow \ \frac{2\Omega C_s}{\pi G \Sigma_0} > 1 \tag{16}\]であれば安定とわかります。
今までは\(\Omega = (定数)\)と考えてきましたが、上式において\(2\Omega \rightarrow \kappa\)と置き換えることで、一般の差動回転円盤の場合にも適用することができます。\(\kappa\)はエピサイクリック振動数で
\[\kappa^2 = \frac{1}{r^3} \frac{d}{dr} (r^4 \Omega^2) \tag{17}\]です。このときの
\[Q \equiv \frac{\kappa C_s}{\pi G \Sigma_0} \tag{18}\]をトゥームレのQパラメータ(Toomre’s Q parameter)と呼びます。\(Q>1\)のとき、円盤は安定に回転を続け、\(Q<1\)のときは円盤内で流体が自己重力による収縮を起こし、惑星や連星などの形成に繋がります。
参考文献
[1] 観山正見, 野本憲一, 二間瀬敏史, “天体物理学の基礎I”
[2] 福江純, 和田桂一, 梅村雅之, “宇宙流体力学の基礎”