超光速運動
超光速運動とは?
最近こんなニュースが目に飛び込んできました。
光速の99%以上! M87のジェットの速度が「チャンドラ」の観測によって判明
昨年2019、EHT(Event Horizon Telescope, イベント・ホライズン・テレスコープ)によってブラックホールの存在が直接撮像されたM87の中心部から、光の速度の99%以上という猛烈なスピードで宇宙ジェットが噴き出しているというものです。記事の中を詳しく読んでいくと…
研究チームによると、ジェットのなかでも超大質量ブラックホールに近い部分(ブラックホールからおよそ900光年ほどの範囲)にみられるX線を放つ2つの塊を観測すると、それぞれ光速の6.3倍と2.4倍で動いているように見えるといいます。ただし、これはあくまでも見かけ上の速度で、実際に光の速度を超えているわけではありません。
なるほど。どうやら宇宙空間で物体が光速度に近い速度で運動を行うと見かけの速度が光速度を超える現象のようです。
ではなぜそのようなことが起こるのでしょうか。それを数式で解説したいと思います。
問題設定
以下のように、AGN(Active Galactic Nuclei, 活動銀河中心核)が勢いよくジェットを吹き出しているとします。その中心部分から光子1が、そして吹き出したジェットの先端から光子2が、それぞれ無限遠方にいる観測者の方向に飛び出してきたとしましょう。
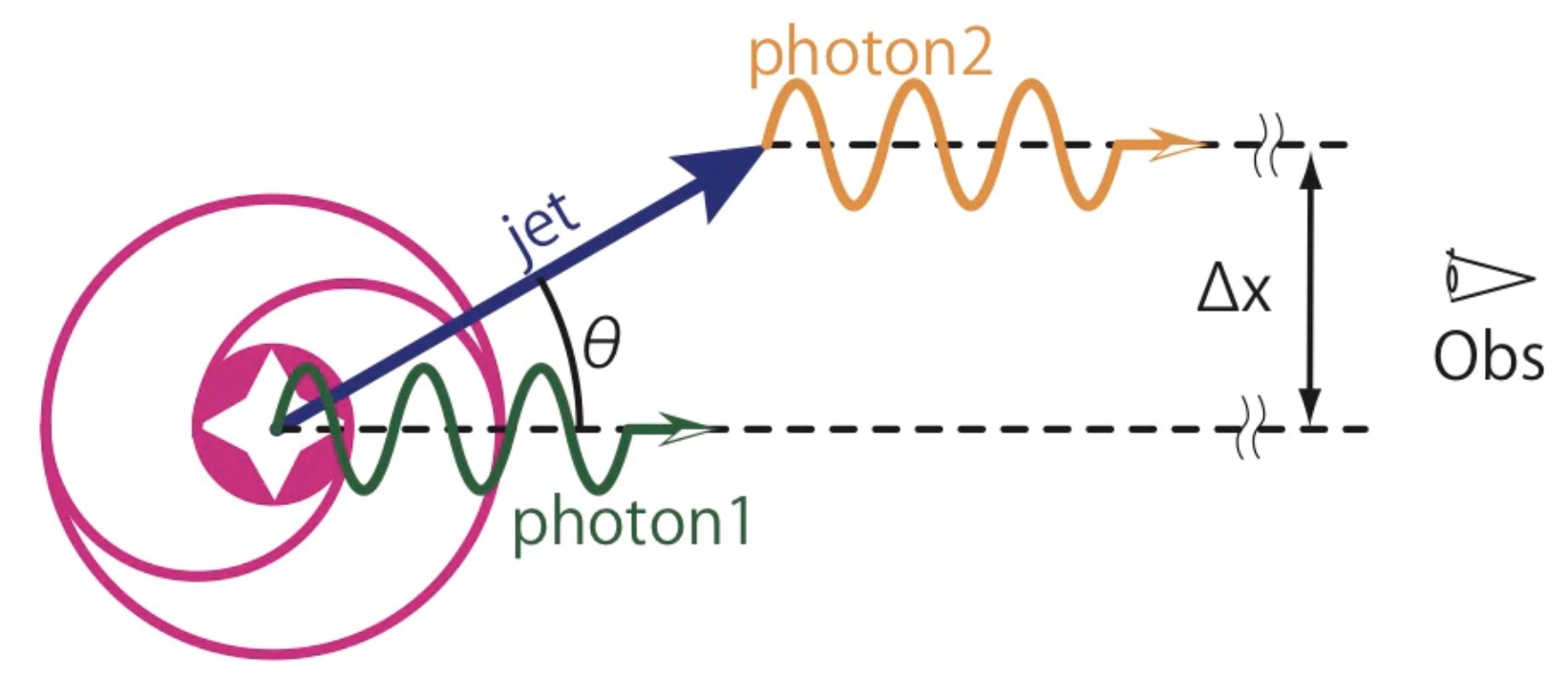
ドップラー効果
上図のようにジェットが角度\(\theta\)方向に速度\(v\)飛び出したとします。\(\Delta t\)だけ時間が経過すると、光子1は観測者に対して
\[\ell_1 = c \Delta t\]だけ近づきます。その間にジェットは
\[\ell_{\rm jet} = v \Delta t \cos \theta\]だけ観測者の方向に近づきます。 そして時刻\(t_0 +\Delta t\)にジェットから観測者方向に光子2が放射されたとしましょう。すると光子1が観測者に届いてから光子2が観測者に届くまでの時間差\(\Delta t'\)は
\[\Delta t' = \frac{\ell_1 - \ell_{\rm jet}}{c} = (1-\beta \cos \theta )\Delta t\]と書けます(ここで\(\beta=v/c\)としました)。
見かけの運動
一方でジェットは天球面上を
\[\Delta x = v \Delta t \sin \theta\]だけ動きます。よって天球面上でのジェットの見かけの運動速度\(\beta_{\rm app} = v_{\rm app} /c\)は
\[\beta_{\rm app} = \frac{1}{c} \frac{\Delta x}{\Delta t'} = \frac{\beta \sin \theta}{1-\beta \cos \theta}\]となります。この式より適当に\(\beta \sim 1\)の値と\(\theta\)を選ぶと、見かけの速度が\(\beta_{\rm app}>1\)となることがわかります。\(\beta_{\rm app}\)と\(\theta\)は観測量なので、この式からジェットの本当の速度\(\beta\)を見積もることも可能です。
余談
\(\beta_{\rm app}\)が最大となる角度$\theta$を求めて見ましょう。
\[\frac{d\beta_{\rm app}}{d\theta} = \frac{\beta \cos \theta (1-\beta \cos \theta) - \beta^2 \sin^2 \theta}{(1-\beta \cos \theta)^2} = \frac{\beta(\cos \theta -\beta)}{(1-\beta \cos \theta)^2} =0\]のとき極大となるので
\[\beta = \cos \theta \Longrightarrow \theta = \cos^{-1} \beta\]よってこのときの\(\beta_{\rm app}\)は
\[\beta_{\rm app} = \frac{\cos \theta \sin \theta}{1-\cos^2 \theta} = \frac{\cos \theta}{\sin \theta} = \cot \theta\]この最大値が1を超えるとき(超光速運動として観測される)ために必要な\(\beta\)の下限値は
\[\beta_{\rm app} (\beta = \cos \theta) = \frac{\cos \theta}{\sin \theta} = \frac{\beta}{\sqrt{1-\beta^2}} >1 \ \Longrightarrow \ \beta > 1/ \sqrt{2} \sim 0.71\]となり、最低でも光速の70%以上の速度でジェットが運動していないと、超光速運動として観測されないことがわかります。
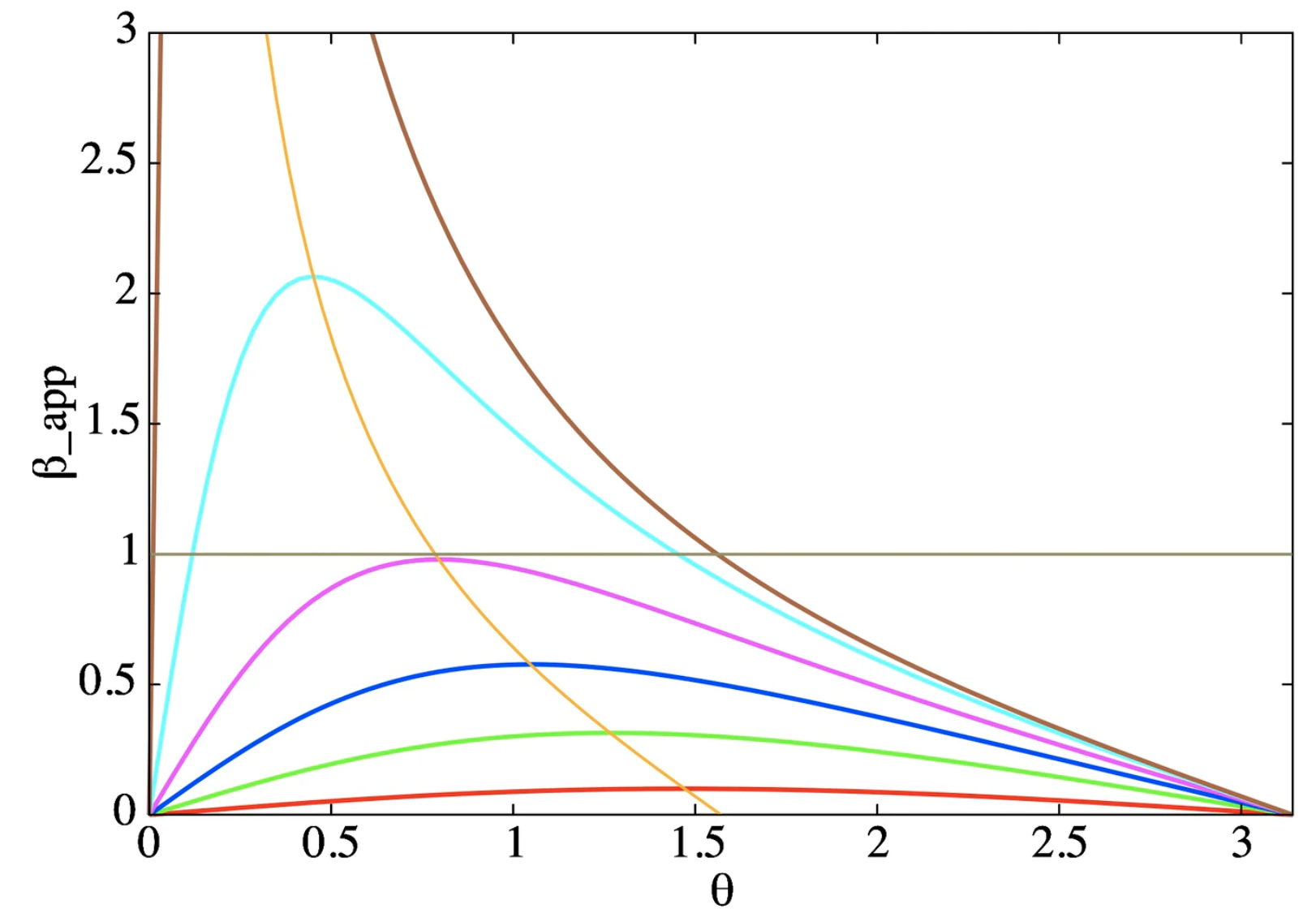
上図は見かけの速度\(\beta_{\rm app}\)を横軸\(\theta\)で図示したものです。red:\(\beta\) = 0.1, green:\(\beta\) = 0.3, blue:\(\beta\) = 0.5, magenda:\(\beta\) = 0.7, cian:\(\beta\) = 0.9, blown:\(\beta\) = 0.99。黄色は\(\beta_{\rm app}\) = \(\cot \theta\)(\(\beta_{\rm app}\) が極大となる線)。