Table of contents

標準降着円盤
参考文献

標準降着円盤

連星系中の中性子星や白色矮星など、いわゆるコンパクト天体周辺には降着円盤(accretion disks)と呼ばれる回転ガス円盤が形成されます。伴星表面からのガス物質がコンパクト天体に落下するときに、ガスが持っている角運動量のために自由落下せず、ガス物質の回転運動の遠心力と重力との釣り合いが生まれます。これにより回転ガス円盤が形成されるのです。
ここでは降着円盤の基本的なモデルである標準降着円盤を考えましょう。「標準」とは

幾何学的に薄く (geometrically thin)
光学的に厚い (optically thick)
軸対称な円盤

であることを意味します。平たく潰れたピザのような恒星が、コンパクト天体を中心に回転していると考えれば良いでしょう。

基礎方程式

半径\(R\)におけるガス円盤の面密度を

\[\Sigma \equiv \int_{-h}^h \rho dz \tag{1}\]

のように、円盤に垂直な方向に積分したものとして定義します。ここで円盤の厚みを\(2h\)としました。円筒座標系での質量保存則は、円筒座標系でのベクトルの発散に注意すると

\[\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \mathbf{v}) = \frac{\partial \rho}{\partial t} + \frac{1}{R} \frac{\partial}{\partial R} (R \rho v_R) = 0\]

です。ここで軸対称性と幾何学的に薄いことから\(\varphi, z\)微分は0としました。この両辺を\(\int_{-h}^h dz\)で積分すれば

\[\frac{\partial \Sigma}{\partial t} + \frac{1}{R} \frac{\partial}{\partial R} (R \Sigma v_R) = 0\tag{2}\]

のようになります。続いて角運動量保存則です。半径\(R\)に位置する幅\(\Delta R\)のリングを考えましょう。このとき、このリングが持つ角運動量は

\[L = 2\pi R \cdot dR \cdot R \Sigma v_\varphi \tag{3}\]

です。\(z\)方向にはあらかじめ積分した形で考えました。この降着円盤は中心のコンパクト天体による重力と遠心力が釣り合った運動をしています。すると

\[\frac{GM}{R^2} = R \Omega_K^2 \ \Longrightarrow \ \Omega_K = \sqrt{\frac{GM}{R^3}} \propto R^{-3/2} \tag{4}\]

のように、内側ほど高速で回転していることがわかります。このような差動回転では速く回転する流体と遅く回転する流体の間に粘性が働くと考えることができます。よって次は\(R\)に垂直な面に働く粘性応力テンソルを考えましょう。今は角運動量保存について着目しているので、中でも\(\varphi\)方向に働く応力に興味があります。よって\(R\)に垂直な面に働く\(\varphi\)方向の応力テンソルの成分を\(\tilde{\sigma}_{R\varphi}\)と書くと、これは

\[\tilde{\sigma}_{R\varphi} = \eta \left( \frac{\partial v_R}{\partial x_\varphi} + \frac{\partial v_\varphi}{\partial x_R}\right) = \eta \left( \frac{1}{R} \frac{\partial v_R}{\partial \varphi} + \frac{\partial v_\varphi}{\partial R} - \frac{v_\varphi}{R}\right) = \rho \nu R \frac{\partial}{\partial R} \left( \frac{v_\varphi}{R}\right) = \rho \nu R \frac{\partial \Omega}{\partial R}\]

のようになります。ここで\(\eta\)は粘性係数、\(\nu = \eta / \rho\)は動粘性係数です。さらに途中、この系は軸対称なので\(\frac{\partial}{\partial \varphi} = 0\)としました。問題設定から応力テンソルの\(R\varphi\)成分のみがゼロでないと考えられるので、半径\(R\)にあるガスリングに働くトルクは

\[N = R \mathbf{e}_R \times \tilde{\sigma}_{R\varphi} \mathbf{e}_\varphi = R \tilde{\sigma}_{R\varphi} \mathbf{e}_z\]

を、円周と円盤に垂直な方向に積分したものとなります。よってガスリングに働く全トルクは

\[G(R, t) = 2\pi R \cdot R \int_{-h}^h \tilde{\sigma}_{R \varphi} dz = 2\pi R^3 \nu \Sigma \frac{\partial \Omega}{\partial R} \tag{5}\]

となります。下図より、ガスリングの単位時間あたりの角運動量の変化は

\[\begin{aligned} &(ガスリングより外側にいるガスからのトルク) - (ガスリングより内側にいるガスからのトルク) \\ & \qquad + (単位時間にRから流入するガスの角運動量) - (単位時間にR+\Delta Rから流出するガスの角運動量) \end{aligned}\]

と表されます。

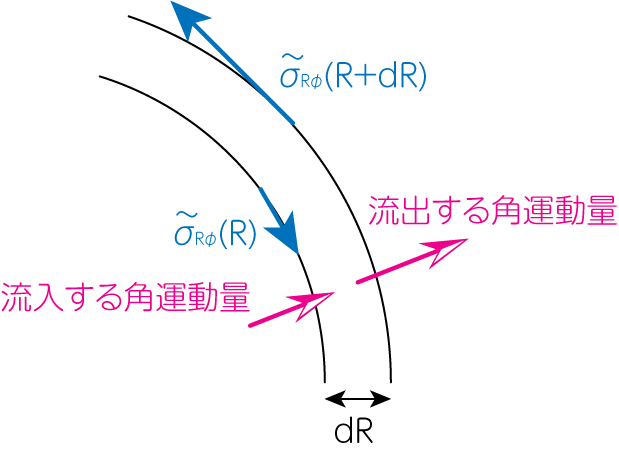
よって

\[\begin{aligned} \frac{\partial L}{\partial t} &= G(R + \Delta R, t) - G(R, t) \\ & \qquad + R \cdot 2\pi R \Sigma(R, t) v_R(R, t) v_\varphi (R, t) - (R+\Delta R) \cdot 2\pi (R + \Delta R) \Sigma(R + \Delta, t) v_R (R+\Delta R, t) v_\varphi (R +\Delta R, t) \end{aligned}\]

(3), (5)式をこの式に代入し、両辺を\(2\pi \Delta R\)で割ります。さらに\(\Delta R \rightarrow 0\)の極限を取ると、微分の定義から

\[\frac{\partial}{\partial t} (R^2 \Sigma v_\varphi) = \frac{\partial}{\partial R} \left( R^3 \nu \Sigma \frac{\partial \Omega}{\partial R}\right) - \frac{\partial}{\partial R} (R^2 \Sigma v_R v_\varphi) \tag{6}\]

となります。

もちろん、[円筒座標系における角運動量保存則](/mhd/momentum_cyl)から導くことも可能です。その場合、粘性応力テンソルにより及ぼされる力を(幾何学的な因子も含めて)しっかりと円筒座標系で考える必要があります。
今回はその難しさを省くためにこのような導出にしました。

円盤を構成するガスの拡散方程式

(6)式を変形します。\(\Omega = v_\varphi / R\)を用いると

\[R^3 \frac{\partial}{\partial t} (\Sigma \Omega) + \Sigma R v_R \frac{\partial}{\partial R} (R^2 \Omega) + R^2\Omega \frac{\partial}{\partial R} (\Sigma R v_R) = \frac{\partial}{\partial R} \left( R^3 \nu \Sigma \frac{\partial \Omega}{\partial R}\right)\]

系は定常に回転していると考え、\(\frac{\partial \Omega}{\partial t} = 0\)とします。さらに(2)式を用いると

\[R^3 \Omega \frac{\partial \Sigma}{\partial t} + \Sigma R v_R \frac{\partial}{\partial R} (R^2 \Omega) - R^3 \Omega \frac{\partial \Sigma}{\partial R} = \Sigma R v_R \frac{\partial}{\partial R} (R^2 \Omega) = \frac{\partial}{\partial R} \left( R^3 \nu \Sigma \frac{\partial \Omega}{\partial R}\right)\]

を得ます。これより

\[\Sigma R v_R = - \frac{1}{\frac{\partial}{\partial R} (R^2 \Omega)} \frac{\partial}{\partial R} \left\{ R^3 \nu \Sigma \left( - \frac{\partial \Omega}{\partial R} \right)\right\}\]

この両辺を\(R\)で微分すると

\[\frac{\partial}{\partial R} (\Sigma R v_R) \underbrace{=}_{(2)} - R \frac{\partial \Sigma}{\partial t} = - \frac{\partial}{\partial R} \left[ \frac{1}{\frac{\partial}{\partial R} (R^2 \Omega)} \frac{\partial}{\partial R} \left\{ R^3 \nu \Sigma \left( - \frac{\partial \Omega}{\partial R} \right)\right\}\right]\]

となります。ここで\(\nu = (定数)\)、さらに質量\(M\)の中性子星やブラックホールなどの中心天体による重力が存在するとして\(\Omega = \Omega_K\)とすると

\[\begin{aligned} \frac{\partial \Sigma}{\partial R} &= \frac{\nu}{R} \frac{\partial}{\partial R} \left\{ \frac{2}{\sqrt{\frac{GM}{R}}} \frac{\partial}{\partial R} \left( \Sigma R^3 \frac{3}{2} \sqrt{\frac{GM}{R^5}}\right)\right\} = \frac{3\nu}{R} \frac{\partial}{\partial R} \left\{ \frac{1}{R \sqrt{\frac{GM}{R^3}}} \frac{\partial}{\partial R} \left( \Sigma R^2 \sqrt{\frac{GM}{R^3}}\right)\right\} \\ &\underbrace{=}_{(4)} \frac{3\nu}{R} \frac{\partial}{\partial R} \left\{ \frac{1}{R \Omega_K} \frac{\partial}{\partial R} ( \Sigma R^2 \Omega_K )\right\} = \frac{3\nu}{R} \frac{\partial}{\partial R} \left\{ \frac{1}{R\Omega_K} \left( R^2\Omega_K \frac{\partial \Sigma}{\partial R} + 2R\Sigma \Omega_K + R^2 \Sigma \frac{\partial \Omega_K}{\partial R}\right)\right\} \\ &= \frac{3\nu}{R} \frac{\partial}{\partial R} \left\{ \frac{1}{R\Omega_K} \left( R^2\Omega_K \frac{\partial \Sigma}{\partial R} + 2R\Sigma \Omega_K -\frac{3}{2} R^2 \Sigma \frac{\Omega_K}{R}\right)\right\} = \frac{3\nu}{R} \frac{\partial}{\partial R} \left( R \frac{\partial \Sigma}{\partial R} + \frac{1}{2} \Sigma\right) \end{aligned}\]

ここで\(x = 2\sqrt{R}\)のように置換すると

\[R = \frac{x^2}{4}, \quad \frac{\partial}{\partial R} = \frac{\partial x}{\partial R} = \frac{1}{\sqrt{R}} \frac{\partial}{\partial x} = \frac{2}{x} \frac{\partial}{\partial x}\]

より

\[\frac{\partial \Sigma}{\partial t} = \frac{12\nu}{x^2} \frac{2}{x} \frac{\partial}{\partial x} \left( \frac{2}{x} \frac{\partial \Sigma}{\partial x} \frac{x^2}{4} + \frac{1}{2} \Sigma\right) = \frac{12 \nu}{x^3} \frac{\partial^2}{\partial x^2} (x\Sigma)\]

以上より

\[\frac{\partial}{\partial t} (\sqrt{R} \Sigma) = \frac{12\nu}{x^2} \frac{\partial^2}{\partial x^2} (\sqrt{R} \Sigma) \tag{7}\]

を得ます。左辺が時間1階微分、右辺が空間2階微分の形なので、これは拡散方程式を表すことがわかります。粘性の効果を入れているため、それによりガスが拡散していくという直感に一致します。

解析解

(7)式において\(\sqrt{R} \Sigma = T(t) S(x)\)のように変数分離を行うと

\[S \frac{\partial T}{\partial t} = T \frac{12\nu}{x^2} \frac{\partial^2 S}{\partial x^2} \ \Longrightarrow \ \frac{1}{T} \frac{\partial T}{\partial t} = \frac{1}{S} \frac{12\nu}{x^2} \frac{\partial^2 S}{\partial x^2}\]

左辺は\(t\)のみの関数、右辺は\(x\)のみの関数なので

\[\frac{1}{T} \frac{\partial T}{\partial t} = \frac{1}{S} \frac{12\nu}{x^2} \frac{\partial^2 S}{\partial x^2} = -\lambda^2\]

のように定数\(-\lambda^2\)を用いて書くことができます。まずは\(T\)について考えてみましょう。

\[\frac{\partial T}{\partial t} = -\lambda^2 T \ \Longrightarrow \ T(t) = T_0 (\lambda) e^{-\lambda^2 t} \tag{8}\]

同様に\(S\)についても考えましょう。

\[\frac{\partial^2 S}{\partial x^2} + \underbrace{\frac{\lambda^2}{12\nu}}_{\equiv \alpha} x^2 S \tag{9} = 0\]

ここで\(S(x) = \sqrt{x} Z(x)\)とおくと

\[\frac{\partial S}{\partial x} = \frac{1}{2 \sqrt{x}} Z + \sqrt{x} \frac{\partial Z}{\partial x}, \quad \frac{\partial^2 S}{\partial x^2} = - \frac{1}{4\sqrt{x^3}} Z + \frac{1}{2 \sqrt{x}} \frac{\partial Z}{\partial x} + \frac{1}{2 \sqrt{x}} \frac{\partial Z}{\partial x} + \sqrt{x} \frac{\partial^2 Z}{\partial x^2}\]

より

\[\sqrt{x} \frac{\partial^2 Z}{\partial x^2} + \frac{1}{\sqrt{x}} \frac{\partial Z}{\partial x} - \frac{1}{4\sqrt{x^3}} Z + \alpha \sqrt{x^{5}} Z = 0 \ \Longrightarrow \ \frac{\partial^2 Z}{\partial x^2} + \frac{1}{x} \frac{\partial Z}{\partial x} + \left( -\frac{1}{4 x^2} + \alpha x^2\right) Z = 0\]

です。さらに\(\xi = x^2\)と置換します。

\[\frac{\partial}{\partial x} = \frac{\partial \xi}{\partial x} \frac{\partial}{\partial \xi} = 2x \frac{\partial}{\partial \xi}, \quad \frac{\partial^2}{\partial x^2} = 2 \frac{\partial}{\partial \xi} + 2x \frac{\partial \xi}{\partial x} \frac{\partial}{\partial \xi} \frac{\partial}{\partial \xi} = 2 \frac{\partial}{\partial \xi} + 4 \xi \frac{\partial^2}{\partial \xi^2}\]

より

\[4\xi \frac{\partial^2 Z}{\partial \xi^2} + 2 \frac{\partial Z}{\partial \xi} + 2 \frac{\partial Z}{\partial \xi} + \left( \alpha \xi - \frac{1}{4\xi}\right) Z = 0 \ \Longrightarrow \ \frac{\partial^2 Z}{\partial \xi^2} + \frac{1}{\xi} \frac{\partial Z}{\partial \xi} + \left( \frac{\alpha}{4} - \frac{1}{16 \xi^2}\right) Z = 0\]

最後に\(\zeta = \sqrt{\alpha} \xi / 2\)と置換して整理すると

\[\frac{4}{\alpha} \frac{\partial^2 Z}{\partial \zeta^2} + \frac{4}{\alpha \zeta} \frac{\partial Z}{\partial \zeta} + \left( \frac{\alpha}{4} - \frac{\alpha/4}{16 \zeta^2}\right) Z = 0 \ \Longrightarrow \ \frac{\partial^2 Z}{\partial \zeta^2} + \frac{1}{\zeta} \frac{\partial Z}{\partial \zeta} + \left( 1 - \frac{(1/4)^2}{\zeta^2}\right) Z = 0\]

この方程式はベッセルの微分方程式に一致します。よってこの方程式の解は

\[Z(x) = J_{1/4} (\zeta) = J_{1/4} (\sqrt{\alpha} \xi /2) = J_{1/4} (\sqrt{\alpha} x^2 / 2)\]

です。長くなりましたが、以上から求めたかった(9)式の解は

\[S(x) = A(\lambda) \sqrt{x} J_{1/4} (\sqrt{\alpha} x^2 / 2) \underbrace{=}_{x = 2\sqrt{R}} A(\lambda) \sqrt{2} R^{1/4} J_{1/4} \left( \sqrt{\frac{\lambda^2}{3\nu}} R \right) = \sqrt{2} A(\lambda) R^{1/4} J_{1/4} (f\lambda R)\]

となります。\(f = 1/ \sqrt{3\nu}\)としました。
\(\lambda\)は\(t, x\)に依存しない定数なので、(7)式の解は実際には様々な\(\lambda\)の重ね合わせとして表現されるはずです。よって最終的に求めたい\(\sqrt{R} \Sigma(R, t)\)は

\[\sqrt{R} \Sigma(R, t) = \int_0^\infty T_0 (\lambda) e^{-\lambda^2 t} \sqrt{2} A(\lambda) R^{1/4} J_{1/4} (f\lambda R) d\lambda = \int_0^\infty \underbrace{T_0 (\lambda) A(\lambda)}_{\equiv C(\lambda)} e^{-\lambda^2 t} R^{1/4} J_{1/4} (f\lambda R) d\lambda\]

よって

\[\Sigma(R, t) = \sqrt{2} \int_0^\infty C(\lambda) e^{-\lambda^2 t} R^{-1/4} J_{1/4} (f\lambda R) d\lambda \tag{10}\]

と求まります。

簡単な初期条件(デルタ関数)での計算

より簡単にするために、初期条件として

\[\Sigma(R, t=0) = \frac{m}{2\pi R_0} \delta (R-R_0) \tag{11}\]

を考えましょう。これは半径\(R=R_0\)の位置に質量\(m\)のガスが溜まっている場合に相当します。ベッセル関数の展開定理より

\[g(R) = \int_0^\infty \bar{g}(\alpha) J_\nu (\alpha R) dR, \quad \bar{g}(\alpha) = \alpha \int_0^\infty R g(R) J_\nu (\alpha R) dR \tag{12}\] \[\int_0^\infty R J_\nu (\alpha R) J_\nu (\bar{\alpha} R) dR = \frac{\delta(\alpha -\bar{\alpha})}{\alpha}, \quad \int_0^\infty \alpha J_\nu (\alpha R) J_\nu (\alpha \bar{R}) d\alpha = \frac{\delta(R-\bar{R})}{R} \tag{13}\]

です。これらを用いて初期条件がデルタ関数の場合の解析解を導出しましょう。まず

\[\delta(R-R_0) = \int_0^\infty D(\lambda) J_\nu (\lambda R) d\lambda = \int_0^\infty D(\bar{\lambda}) J_\nu (\bar{\lambda} R) d\bar{\lambda}\]

とします。両辺に\(R J(\lambda R)\)をかけ、それを\(R\)で積分します。すると

\[\begin{align} &R_0 J_\nu(\lambda R_0) = \int_0^\infty D(\bar{\lambda}) \underbrace{\left( \int_0^\infty R J_\nu (\bar{\lambda} R) J_\nu (\lambda R) dR\right)}_{(13)} d\bar{\lambda} = \int_0^\infty D(\bar{\lambda}) \frac{\delta (\bar{\lambda}-\lambda)}{\bar{\lambda}} d\bar{\lambda} = \frac{D(\lambda)}{\lambda} \notag \\ &\Longrightarrow D(\lambda) = \lambda R_0 J_\nu (\lambda R_0) \tag{14} \end{align}\]

を得ます。(10)式において\(t=0\)として

\[\Sigma (R, t=0) = \sqrt{2} \int_0^\infty C(\bar{\lambda}) R^{-1/4} J_{1/4} (f\bar{\lambda} R) d\bar{\lambda} = \frac{m}{2\pi R_0} \delta (R-R_0)\]

です。両辺に\(\frac{R^{5/4}}{\sqrt{2}} J_{1/4} (fR\lambda)\)をかけて、それを\(R\)で積分すると

\[\int_0^\infty C(\bar{\lambda}) \left( \int_0^\infty R J_{1/4} (f\bar{\lambda} R) J_{1/4} (f\lambda R) dR \right) d\bar{\lambda} = \frac{m}{2\sqrt{2} \pi } R_0^{1/4} J_{1/4} (fR_0 \lambda)\]

となります。左辺の\(R\)積分において(13)式を適用すると

\[\int_0^\infty C(\bar{\lambda}) \frac{\delta (f\bar{\lambda} - f\lambda)}{f\bar{\lambda}} d\bar{\lambda} = \int_0^\infty C(\bar{\lambda}) \frac{\delta (\bar{\lambda} - \lambda)}{f^2\bar{\lambda}} d\bar{\lambda} = \frac{C(\lambda)}{f^2 \lambda}\]

より

\[C(\lambda) = \frac{m}{2\sqrt{2} \pi} f^2 \lambda R_0^{1/4} J_{1/4} (fR_0 \lambda)\]

とわかります。これを(10)式に代入すれば

\[\begin{aligned} \Sigma (R, t) &= \frac{mf^2}{2\pi} \left( \frac{R_0}{R}\right)^{1/4} \int_0^\infty e^{-\lambda^2 t} \lambda J_{1/4} (f\lambda R) J_{1/4} (f\lambda R_0) d\lambda \\ &= \frac{mf^2}{2\pi} \left( \frac{R_0}{R}\right)^{1/4} \frac{1}{2t} \exp \left( - \frac{f^2 (R^2 + R_0^2)}{4t}\right) I_{1/4} \left( \frac{f^2 RR_0}{2t}\right) \end{aligned}\]

と求まります。ここで以下の積分公式を用いました。

\[\int_0^\infty e^{-a x^2} x J_\nu (px) J_\nu (qx) dx = \frac{1}{2a} \exp \left( - \frac{p^2 + q^2}{4a}\right) I_\nu \left(\frac{pq}{2a} \right)\]

\(I_\nu\)は第一種変形ベッセル関数です。
拡散の時間スケール\(t_\mathrm{diff} = \frac{R_0^2}{(12\nu)} = R_0^2 f^2 / 4\)を用いて時間を規格化した\(t^\ast = t/ t_\mathrm{diff}\)、そして規格化された長さ\(R^\ast = R / R_0\)を用いて先程の式を書き換えると

\[\Sigma (R^\ast, t^\ast) = \frac{m}{\pi R_0^2} \frac{(R^\ast)^{-1/4}}{t^\ast} \exp \left( - \frac{(R^\ast)^2 + 1}{t^\ast}\right) I_{1/4} \left(\frac{2R^\ast}{t^\ast} \right) \tag{15}\]

のようになります。

可視化

(15)式から\(\pi R_0^2 \Sigma /m\)の時間発展を動画にすると、次のようになります。この可視化では\(R_0 = 1.0\)としています。

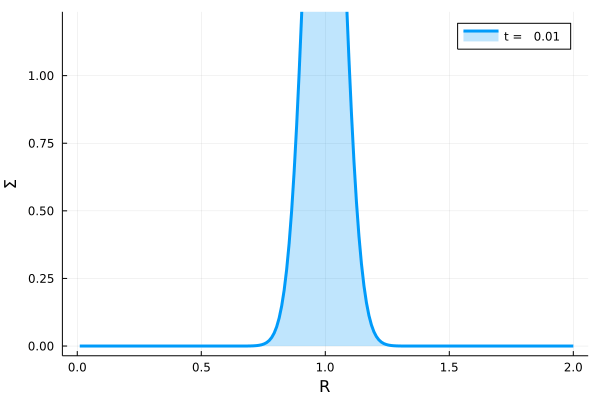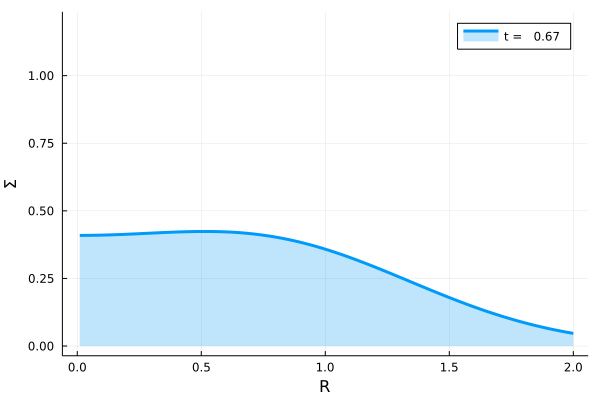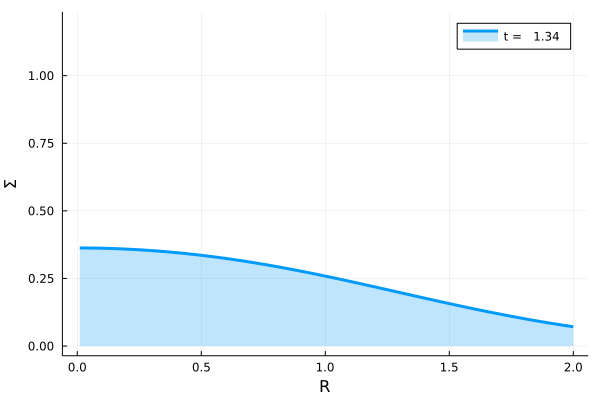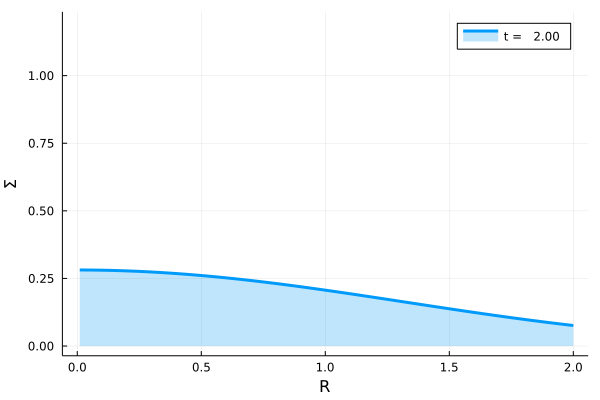
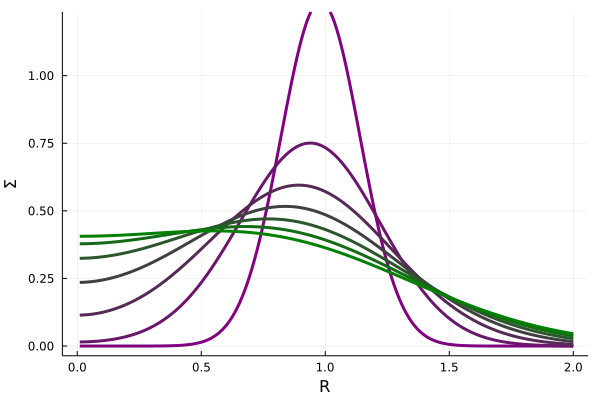
次の図は各時刻でのスナップショットです。紫色から順に、緑色に向かって時間が経過しています。初期にデルタ関数的に分布していたガスは、粘性により角運動量を得るものと失うものとに別れます。角運動量を得たガスは中心天体から離れた距離に移動し、角運動量を失ったガスは\(R=0\)に位置する中心天体に降り注ぎます。

それぞれの可視化に用いたJulia言語のソースコードを以下に示します。まずはgif動画を作成するコードです。

using Plots
using SpecialFunctions
using Printf

# compute gas density of standard disk
function standard_disk(t, R)
  return R^(-0.25) / t * exp(-(R^2+1)/t) * besseli(0.25, 2*R/t)
end

# set R coordinate
Rmax = 2.0
Rmin = 0.0
nR = 200
Rs = range(Rmin, Rmax, length=nR)
# set t
tmax = 2.0
tmin = 0.01
nt = 200
ts = range(tmin, tmax, length=nt)
# initialize animation frame
a = Animation()
# set zero vector for filling image
density0 = zeros(nR)
##### main loop for gif animation start #####
for t in ts
  # get gas density
  density = standard_disk.(t, Rs)
  # set label for plot
  label_string = string("t = " , @sprintf("%6.2f", t))
  # make plot
  p_gif = plot(Rs, density, fillrange=density0, fillalpha=0.25, xlim=[Rmin, Rmax], ylim=[0, 1.2], linewidth=3, legend=:topright, xlabel="R", ylabel="Σ", label=label_string)
  # convert to animation frame
  frame(a, p_gif)
end
###### main loop for gif animation end ######
# convert animation frame to gif
gif(a, "standard_disk.gif", fps=30)

続いてスナップショットを作成したコードです。

using Plots
using SpecialFunctions

# compute gas density of standard disk
function standard_disk(t, R)
  return R^(-0.25) / t * exp(-(R^2+1)/t) * besseli(0.25, 2*R/t)
end

# set R coordinate
Rmax = 2.0
Rmin = 0.0
nR = 200
Rs = range(Rmin, Rmax, length=nR)
# set time step list
ts = [0.05, 0.15, 0.25, 0.35, 0.45, 0.55, 0.65]
# set the number of time step
nstep = length(ts)
# make color palette
color_list = reshape(range(colorant"purple", stop=colorant"green", length=nstep), 1, nstep);
# initialize array of densities and labels
densities = []
##### main loop for snapshot plot start #####
for n in 1:nstep
  # get gas density
  density = standard_disk.(ts[n], Rs)
  # add to array
  push!(densities, density)
end
###### main loop for snapshot plot end ######
# make plot
p_snap = plot(Rs, densities, linecolor=color_list, xlim=[Rmin, Rmax], ylim=[0, 1.2], linewidth=3, legend=:topright, xlabel="R", ylabel="Σ", label=false)
# save plot
savefig(p_snap, "standard_disk_03.png")

参考文献

福江純, 和田圭一, 梅村雅之, “宇宙流体力学の基礎”
柴田一成, 福江純, 松元亮治, 嶺重慎, “活動する宇宙”