Table of contents
パルサーグリッチ
パルサーの回転エネルギーが電磁放射や粒子加速で失われることで、パルサーのパルス周期は徐々に長くなって(スピンダウンして)いきます。 しかしいくつかのパルサーでは、パルス周期が突然短い時間スケールで短くなる(スピンアップする)現象が確認されており、これをグリッチ(glitches)と呼びます。 グリッチが起きてパルス周期が短くなった後、徐々に元のパルス周期に戻っていきます。
グリッチの原因
中性子星は内部コアと外部のクラストから構成されています。 コアとクラストの間には回転のズレが生じており、コアの自転角速度がわずかに速いとされています。 時間と共にコアとクラストの回転速度が大きくなると、ある時点でコアが持つ角運動量がクラストに輸送され、両者の回転速度が等しくなります。 これがグリッチの原因として考えられているモデルの一つです。 このモデルの理解には、超流動体となっているコアでの渦糸のダイナミクスが必要となります。
その他にも、クラストで起こる地震 (starquake, crustquake) や、中性子星内部の磁束管と渦糸との相互作用モデルなどが提案されていますが、まだ未解明な部分が多く残っています。
グリッチの分類
Normal glitches
パルサーのスピン周波数を\(\nu\)、グリッチにより発生するスピン周波数のジャンプ\(\Delta \nu\)としたときに、\(10^{-12} \lesssim \Delta \nu / \nu \lesssim 10^{-3}\)の範囲にあるものを、通常のグリッチに分類します。 グリッチによりスピンアップする時間スケールは5秒以下から40秒以下など、様々です。 このような様子は、200のパルサーで起こった650以上のグリッチで見られています。
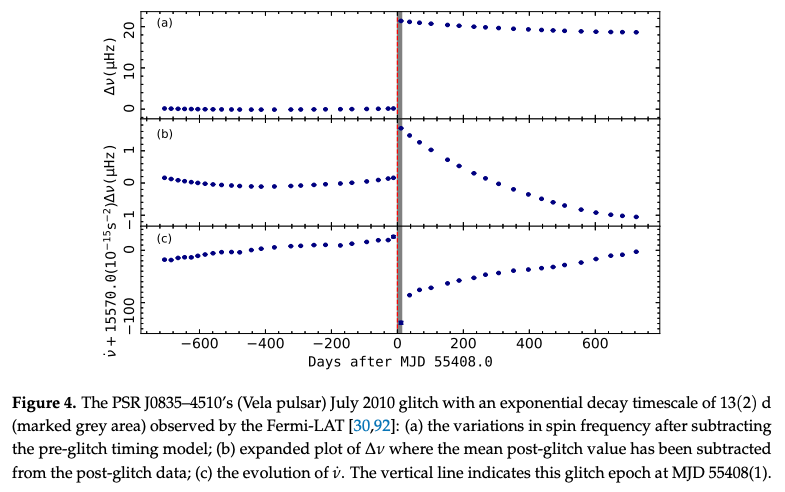
Zhou et al. (2022)より。横軸の0がグリッチ発生時間を表す。
Slow glitches
スピン周波数\(\nu\)がゆっくりと増加するグリッチです。 さらにスピンダウン率\(\dot{\nu}\)も数ヶ月かけて減少していき、長い時間スケールをかけて元のスピンに戻ります。 このようなものは、7つのパルサーで起こった31のグリッチでしか観測されていません。 これを説明するモデルとして、クラスト内部の突然の温度上昇や、ただ単にパルサー自転の位相・スピン・スピンダウン率のランダムな変動によるもの、などが考えられています。
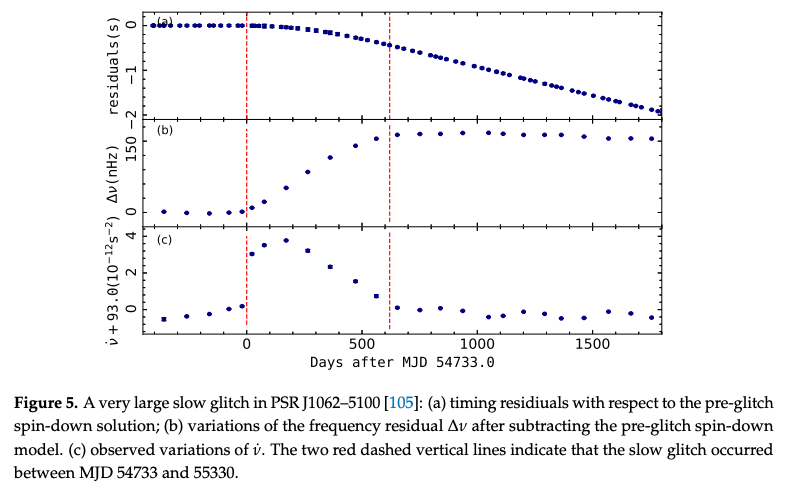
Zhou et al. (2022)より。図の赤破線はグリッチの発生時間と終了時間を表す。
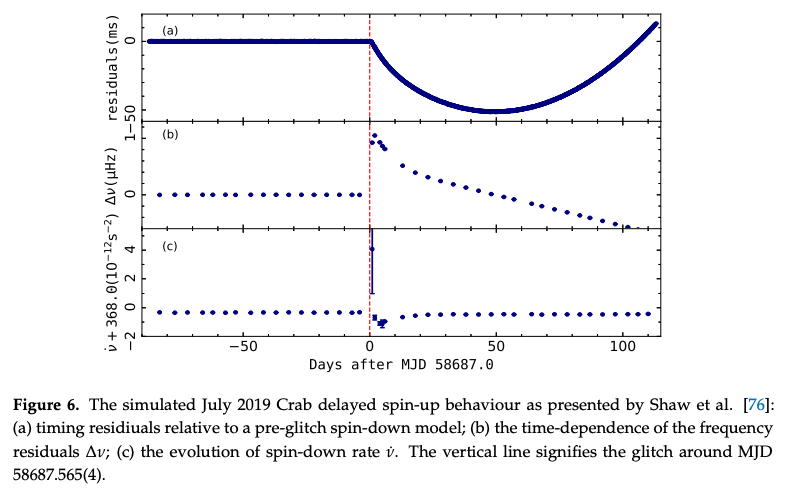
Delayed spin-up
これはグリッチ発生直後に短い時間で\(\nu\)が指数的に増加、その後急速に減少するようなものを指します。 このタイプのグリッチは、かにパルサーで6回起こるなどが観測されています。 若いマグネター内部の変化が磁気圏の構造を大きく変化させることで、大きなグリッチが起こることが指摘されていますが、詳しいことはよくわかっていません。
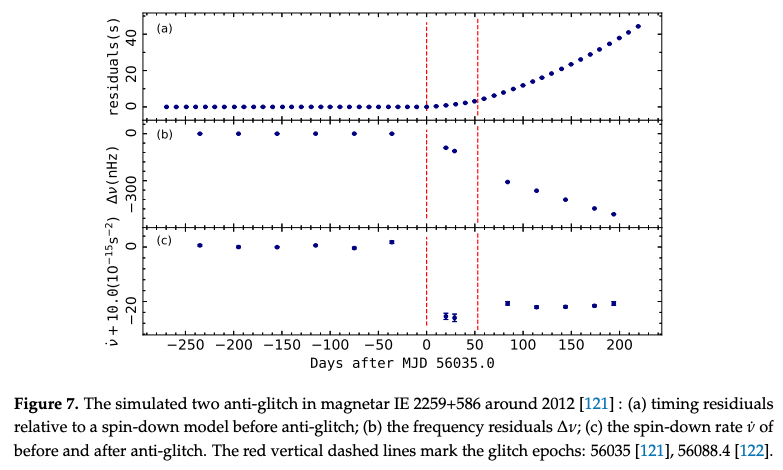
Anti-glitches
これまではスピンアップする現象をグリッチと呼んでいましたが、中には突然スピンダウンする現象も観測されています。 これをanti-glitches (反グリッチ)と呼ばれています。 X線アウトバーストや超大光度X線源 (ultraluminous X-ray sources: ULXs)で観測されていることから、パルサーへの降着が引き金となっているとされています。 マグネターでのウィンドブレーキング・パルサーと小天体との衝突・内部のトロイダル磁場成分の減衰・渦糸の崩壊など、様々なシナリオが研究されています。
グリッチ後の挙動のモデル化
グリッチにより一時的にスピンアップした後の、パルサーの角速度\(\Omega\)の挙動についてモデル化し、それを解いてみましょう。 まずパルサーの角速度\(\Omega\)は、私たちが観測可能な自転角速度を意味します。 これは主に荷電粒子からなり、これがパルサーのビームを発生させていると考えることができます。 この部分の慣性モーメントを\(I_c\)としましょう。 そしてこれとは別の要素として、中性子星の固体クラスト中の超流動中性子からなる成分が、角速度\(\Omega_n\)で自転しているとします。 この部分の慣性モーメントは\(I_n\)のように書くことにします。
グリッチにより、角運動量が内部から外部に輸送され、外側にいる荷電粒子成分の角速度が一時的に速くなります。 その後、一時的に速くなった外側の回転エネルギーの一部は再び内側に輸送され、内側の超流動中性子成分の回転を速めます。 さらに外側の回転エネルギーの一部は、荷電粒子による放射などにより失われていきます。 これらを微分方程式としてモデル化すると、以下のような2つの式になります。
ここで、\(\alpha\)は放射などにより回転エネルギーが失われることを表すもの、そして\(\tau_c\)はクラスト内の角運動量の拡散の時間スケールを表すものです。 以下では簡単のため、\(\alpha, \tau_c\)は定数であるとして式変形を行いましょう。 \(\Delta \equiv \Omega - \Omega_n\)のようにすると、(1), (2)式は
\[\frac{d\Omega}{dt} = - \frac{\alpha}{I_c} - \frac{\Delta}{\tau_c} \tag{3}\] \[\frac{d\Omega_n}{dt} = \frac{I_c \Delta}{I_n \tau_c} \tag{4}\]のようになります。 これらの式の辺々を引き算して
\[\frac{d\Delta}{dt} = - \frac{\alpha}{I_c} - \left( \frac{1}{\tau_c} + \frac{I_c}{I_n \tau_c}\right) \Delta = - \frac{1}{\tau_c} \frac{I_c + I_n}{I_n} \Delta - \frac{\alpha}{I_c} = - \frac{1}{\tau} \Delta - \frac{\alpha}{I_c} \tag{5}\]を得ます。 途中、\(I \equiv I_c + I_n, \tau \equiv \tau_c I_n / I\)のようにしました。 この微分方程式を解くと
\[\frac{d}{dt} \left( \Delta + \frac{\alpha \tau}{I_c}\right) = - \frac{1}{\tau} \left( \Delta + \frac{\alpha \tau}{I_c}\right) \ \Longrightarrow \ \Delta + \frac{\alpha \tau}{I_c} = \Omega_1 e^{-t/\tau} \tag{6}\]となります。 ここで\(\Omega_1\)は定数です。 よって
\[\Omega_n = \Omega - \Omega_1 e^{-t/ \tau} + \frac{\alpha \tau}{I_c} \tag{7}\]を(4)式に代入すると
\[\begin{align} &\frac{d\Omega}{dt} + \frac{\Omega_1}{\tau} e^{-t/\tau} = \frac{I_c}{I_n \tau_c} \left(\Omega_1 e^{-t/\tau} - \frac{\alpha \tau}{I_c} \right) \notag \\ &\Longrightarrow \ \frac{d\Omega}{dt} = \left( \frac{I_c}{I_n \tau_c} - \frac{1}{\tau} \right) \Omega_1 e^{-t/\tau} - \frac{\alpha \tau}{I_n \tau_c} = - \frac{\Omega_1}{\tau_c} e^{-t/\tau} - \frac{\alpha}{I} \notag \\ &\Longrightarrow \ \Omega = \frac{I_n}{I} \Omega_1 e^{-t/\tau} - \frac{\alpha}{I} t + \Omega_2 \tag{8} \end{align}\]のように、\(\Omega\)を求めることができました。 天下り的ですが、積分定数\(\Omega_1, \Omega_2\)の不定性から以下のように書き換えてみましょう。
\[\Omega_0 (t) = \Omega_2 - \frac{\alpha}{I} t - \frac{I_c^2 \Delta \Omega_0 - I_n \alpha \tau}{I I_c}, \quad \Omega_1 = \frac{I_c \Delta \Omega_0 + \alpha \tau}{I_c}\]新しく\(\Delta \Omega_0\)という定数を導入しました。 これらを用いて、(8)式を整理しましょう。
\[\begin{aligned} \Omega &= \Omega_0(t) + \frac{I_n}{I} \frac{I_c \Delta \Omega_0 + \alpha \tau}{I_c} e^{-t/\tau} + \frac{I_c^2 \Delta \Omega_0 - I_n \alpha \tau}{I I_c} \notag \\ &= \Omega_0(t) + \Delta \Omega_0 \frac{I_n}{I} \frac{I_c \Delta \Omega_0 + \alpha \tau}{I_c \Delta \Omega_0 } e^{-t/\tau} + \Delta \Omega_0 \frac{I_c^2 \Delta \Omega_0 - I_n \alpha \tau}{I I_c \Delta \Omega_0} \notag \\ &= \Omega_0(t) + \Delta \Omega_0 \frac{I_n}{I} \left( 1 + \frac{\alpha \tau}{ I_c \Delta \Omega_0}\right) e^{-t/\tau} + \Delta \Omega_0 \frac{(I-I_n)I_c\Delta \Omega_0 - I_n \alpha \tau}{I I_c \Delta \Omega_0} \notag \\ &= \Omega_0(t) + \Delta \Omega_0 \frac{I_n}{I} \left( 1 + \frac{\alpha \tau}{ I_c \Delta \Omega_0}\right) e^{-t/\tau} + \Delta \Omega_0 \left( 1 - \frac{I_n}{I} \frac{I_c \Delta \Omega_0 + \alpha \tau}{I_c \Delta \Omega_0}\right) \end{aligned}\]ここで
\[Q \equiv \frac{I_n}{I} \left( 1 + \frac{\alpha \tau}{I_c \Delta \Omega_0}\right) \tag{9}\]とすると
\[\Omega = \Omega_0 (t) + \Delta \Omega_0 (Q e^{-t/\tau} + 1-Q) \tag{10}\]のように整理されます。 特に\(Q\)のことをhealing parameterと呼び、グリッチ発生から角速度\(\Omega\)が\(\Omega_0\)に近づくまでの度合いを表すパラメータです。
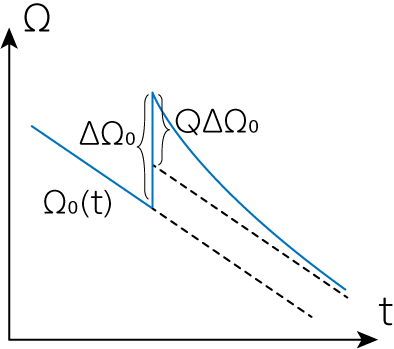
さらに\(\Delta \Omega (t) \equiv \Omega(t) - \Omega_0 (t)\)のように定義すると、(10)式より
\[\Delta \dot{\Omega} = \frac{\Delta \Omega_0 Q}{\tau} e^{-t/\tau} \ \Longrightarrow \ Q = - \frac{\Delta \dot{\Omega} (t=0)}{\Delta \Omega_0} \tau \tag{11}\]のようにして、\(Q\)を求めることができます。 さらに
\[\Delta \ddot{\Omega} = \frac{\Delta \Omega_0 Q}{\tau^2} e^{-t/\tau} \underbrace{=}_{(11)} - \frac{\Delta \dot{\Omega} (t=0)}{\tau} e^{-t/\tau} \ \Longrightarrow \ \tau = - \frac{\Delta \dot{\Omega}(t=0)}{\Delta \ddot{\Omega}(t=0)} \tag{12}\]のようにして、\(\tau\)を求めることができます。 ここで注目したいのは、\(\Delta \dot{\Omega}, \Delta \ddot{\Omega}\)は観測データの解析から求めることができることです。
参考文献
[1] Zhou et al., 2022, “Pulsar Glitches: A Review”
[2] Shapiro & Teukolsky, ”Black holes white dwarfs and neutron stars”