Table of contents
標準降着円盤からのエネルギー放出とそのスペクトル
標準降着円盤とは幾何学的に光学的に厚い、軸対称な円盤でした。以前の記事では定常を仮定して解析を進めましたが、実際には粘性によりガスが降着を起こすため、完全には定常な系ではありません。しかし\(\vert v_R \vert \ll \vert v_\varphi \vert\)のようにとてもゆっくりな降着を考え、定常が成り立っていると考えたのです。
今回はこのような状況にある降着円盤からの質量降着率を考え、そこからのエネルギー放出量と放射エネルギースペクトルを計算してみましょう。
質量降着率
系の定常の仮定から、\(\Sigma, v_R\)は定数と考えることができます。よって質量降着率は
\[\dot{M} = - 2\pi R \Sigma v_R = (定数) \tag{1}\]です。右辺にマイナスがついているのは、\(v_R < 0\)(中心に向かう流れ)のときが質量降着を起こしているときと考えるためです。そしてこの系の角運動量保存則は
\[\frac{\partial}{\partial t} (R^2 \Sigma v_\varphi) = - \frac{\partial}{\partial R} (R^2 \Sigma v_R v_\varphi) + \frac{\partial}{\partial R} \left( R^3 \nu \Sigma \frac{\partial \Omega}{\partial R}\right)\]で与えられるのでした。定常なので左辺の時間微分は0とし、この式の両辺を\(R\)で積分すると
\[\begin{aligned} &\int_{R_\mathrm{in}}^R \frac{\partial }{\partial R} (R^3 \Sigma v_R \Omega) dR = \int_{R_\mathrm{in}}^R \frac{\partial}{\partial R} \left( R^3 \nu \Sigma \frac{\partial \Omega}{\partial R}\right) \\ &\Longrightarrow \ R^3 \Sigma v_R \Omega - R_\mathrm{in}^3 \Sigma (R_\mathrm{in}) v_R (R_\mathrm{in}) \Omega (R_\mathrm{in}) = R^3 \nu \Sigma \frac{\partial \Omega}{\partial R} - R_\mathrm{in}^3 \nu \Sigma (R_\mathrm{in}) \left. \frac{\partial \Omega}{\partial R} \right|_{R_\mathrm{in}} \end{aligned}\]です。ここで積分範囲の\(R_\mathrm{in}\)は円盤の最内縁半径です。今、中性子星やブラックホールのような中心星により円盤が形成されているとすると、\(\Omega = \Omega_K = \sqrt{\frac{GM}{R^3}}\)、さらに円盤の最内縁では\(\frac{\partial \Omega}{\partial R} = 0\)の境界条件が成り立つとします。すると
\[\begin{aligned} &R^3 \Sigma v_R \sqrt{\frac{GM}{R^3}} - R_\mathrm{in}^3 \Sigma(R_\mathrm{in}) v_R (R_\mathrm{in}) \sqrt{\frac{GM}{R_\mathrm{in}^3}} = R^3 \nu \Sigma \left( - \frac{3}{2R} \sqrt{\frac{GM}{R^3}}\right) \\ &\Longrightarrow \ \nu \Sigma = - \frac{2}{3R^2} \left( R^3 \Sigma v_R - R_\mathrm{in}^3 \Sigma (R_\mathrm{in}) v_R(R_\mathrm{in}) \sqrt{\frac{R^3}{R_\mathrm{in}^3}}\right) \end{aligned}\](1)式より、\(R \Sigma v_R = R_\mathrm{in} \Sigma (R_\mathrm{in}) v_R (R_\mathrm{in}) = - \dot{M} / 2\pi = (定数)\)を代入すると
\[\nu \Sigma = \frac{\dot{M}}{3 R^2 \pi} \left( R^2 - R_\mathrm{in}^2 \sqrt{\frac{R^3}{R_\mathrm{in}^3}}\right) = \frac{\dot{M}}{3\pi} \left( 1-\sqrt{\frac{R_\mathrm{in}}{R}}\right) \tag{2}\]となります。
粘性によるエネルギー散逸
粘性は主に流体どうしの摩擦と考えることができます。この摩擦により熱が発生すると考えると、その単位時間単位体積あたりの散逸エネルギーの発生率\(\epsilon\)は
\[\epsilon = \sum_{i, j=1}^3 \tilde{\sigma}_{ij} \frac{\partial v_i}{\partial x_j} = \frac{1}{2\eta} \sum_{i, j=1}^3 \tilde{\sigma}_{ij} \tilde{\sigma}_{ij}\]で与えられます。ここで\(\tilde{\sigma}\)は粘性応力テンソル、\(i, j = 1, 2, 3\)の添字はそれぞれ\(R, \varphi, z\)に対応します。今、系の対称性から\(R\varphi\)成分のみが\(\tilde{\sigma}_{R\varphi} = \rho \nu R \frac{\partial \Omega}{\partial R} \neq 0\)であり、それ以外の成分は0と考えることができるので
\[\epsilon = \frac{1}{2\nu \rho} (\tilde{\sigma}_{R\varphi}^2 + \underbrace{\tilde{\sigma}_{\varphi R}^2}_{= \tilde{\sigma}_{R\varphi}^2}) = \rho \nu \left( R \frac{\partial \Omega_K}{\partial R}\right)^2 \tag{3}\]これを円盤の厚みと半径\(R\)に位置する幅\(\Delta R\)のリングの面積\(2\pi R dR\)の面積で積分すれば、円盤全体からの散逸エネルギー発生率の総量が算出できます。よって
\[\begin{aligned} \int_{R_\mathrm{in}}^R 2\pi R \underbrace{\left( \int_{-h}^h \epsilon dz \right)}_{\equiv \bar{\epsilon}} dR &= 2\pi \int_{R_\mathrm{in}}^R R \nu \left( R \frac{\partial \Omega_K}{\partial R}\right)^2 \left( \int_{-h}^h \rho dz \right) dR = 2\pi \int_{R_\mathrm{in}}^R \nu \Sigma R \left( R \frac{\partial \Omega_K}{\partial R}\right)^2 dR \\ &= -2\pi \int_{R_\mathrm{in}}^R \underbrace{\nu \Sigma}_{(2)} R \frac{9}{4} \frac{GM}{R^3} dR = - \frac{3 GM\dot{M}}{2} \int_{R_\mathrm{in}}^R \left( \frac{1}{R^2}-\sqrt{\frac{R_\mathrm{in}}{R^5}}\right) dR \\ &= - \frac{3 GM\dot{M}}{2} \left[ - \frac{1}{R} + \frac{2}{3} \sqrt{\frac{R_\mathrm{in}}{R^3}}\right]_{R_\mathrm{in}}^R = - \frac{3 GM\dot{M}}{2} \left( - \frac{1}{R} + \frac{2}{3} \sqrt{\frac{R_\mathrm{in}}{R^3}} + \frac{1}{R_\mathrm{in}} - \frac{2}{3 R_\mathrm{in}}\right) \end{aligned}\]となります。積分範囲の\(R_\mathrm{in}\)は、ブラックホールの場合は一般相対論的な効果から\(R_\mathrm{in} = r_g\)(シュバルツシルト半径)としたり、中性子星の場合は磁場の強さにより磁極領域への降着が起きる位置から決定されます。

ここで
\[\bar{\epsilon} = \int_{-h}^h \epsilon dz \underbrace{=}_{(3)} \underbrace{\nu \Sigma}_{(2)} \left( R \frac{\partial \Omega_K}{\partial R}\right)^2 = \frac{\dot{M}}{3\pi} \left( 1-\sqrt{\frac{R}{R_\mathrm{in}}}\right) \left( R \frac{\partial \Omega_K}{\partial R}\right)^2 \tag{4}\]です。簡単のため、円盤は無限遠まで広がっていると考えて\(R \rightarrow \infty\)とすると
\[\int_{R_\mathrm{in}}^\infty 2\pi R \bar{\epsilon} dR = - \frac{1}{2} \frac{GM\dot{M}}{R_\mathrm{in}} \tag{5}\]これは粘性による摩擦熱エネルギーが、粘性がない場合の重力エネルギー\(- \frac{GM \dot{M}}{R_\mathrm{in}}\)の半分であることを意味します。熱エネルギーと重力エネルギーの間にエネルギー等分配が成り立っているとすれば、これは当然の帰結かもしれません。よって半分は輻射として外部に放出、もう半分は重力エネルギーとして中心星に落ちていくことになります。
これはエネルギー交換効率としては50%という驚異的な値です。これはブラックホール発電などのアイデアにも関連しています。
黒体放射による放射スペクトル
粘性によって変換された熱エネルギーのうち、およそ半分がガスの片面から温度\(T\)の黒体放射として放出されると考えましょう。するとこの黒体放射の放射エネルギー総量(振動数で積分したもの)はステファン・ボルツマンの法則で与えられるので
\[\frac{\bar{\epsilon}}{2} = \sigma_\mathrm{SB} T_\mathrm{eff}^4 \ \Longrightarrow \ T_\mathrm{eff} (R) = \left\{ \frac{\dot{M}}{6\pi \sigma_\mathrm{SB}} \left( 1-\sqrt{\frac{R_\mathrm{in}}{R}} \right) \left( R \frac{\partial \Omega_K}{\partial R}\right)^2\right\}^{1/4} = \left\{ \frac{3GM\dot{M}}{8\pi \sigma_\mathrm{SB} R^3} \left( 1-\sqrt{\frac{R_\mathrm{in}}{R}} \right) \right\}^{1/4} \tag{6}\]を得ます。ここで\(\sigma_\mathrm{SR}\)はステファン・ボルツマン定数、\(T_\mathrm{eff} (R)\)は半径\(R\)に位置する降着円盤表面の有効温度です。半径\(R\)の位置にある降着円盤表面からの放射を\(I_\nu (R)\)とすると、これが\(T_\mathrm{eff} (R)\)の黒体放射スペクトルで与えられるので
\[I_\nu (R) = B_\nu (T_\mathrm{eff} (R)) = \frac{2h}{c^2} \frac{\nu^3}{\exp \left(\frac{h\nu}{k_B T_\mathrm{eff}(R)}\right) -1}\]となります。
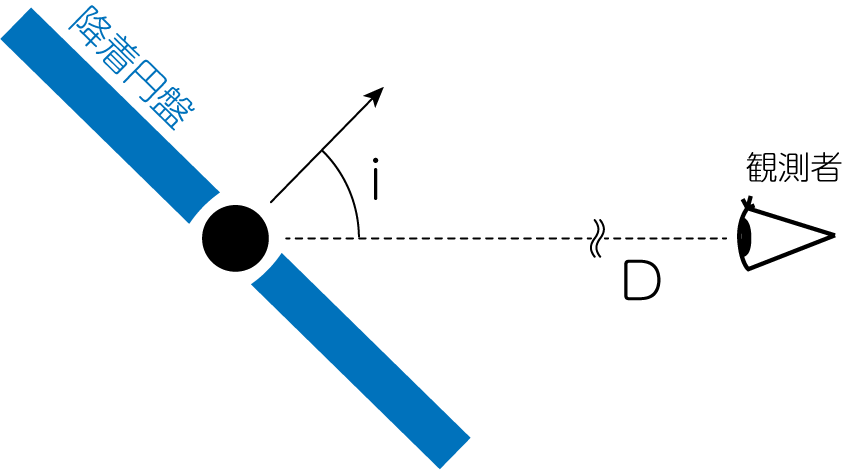
これを無限遠方にる観測者が観測すると考えましょう。観測者に到達するフラックスは、放射が円盤に垂直な方向にしか放出されないと考えて
となります。\(i\)は円盤の傾きと観測者の視線方向が成す角度、\(D\)は観測者と降着円盤までの距離です。
数値計算と簡単な見積もり
中心星の質量\(M\)と中心星への質量降着率\(\dot{M}\)を与えれば、(6)式から半径\(R\)での降着円盤表面温度が分かります。ここから(7)式に従って数値積分を行えば、スペクトルを得ることができます。 以下では\(\dot{M}=10^{-9} M_\odot [\mathrm{yr}^{-1}], M=1.4M_\odot, x_\mathrm{out} = R_\mathrm{out} / R_\mathrm{in} = 10^4\)という共通の値を用いて、以下の3つの場合に数値計算を行います。
- 白色矮星: \(R_\mathrm{in} = 10^9 [\mathrm{cm}]\)
- 中性子星: \(R_\mathrm{in} = 10^6 [\mathrm{cm}]\)
- ブラックホール: \(R_\mathrm{in} = r_g= \frac{2MG}{c^2}\)
下図は
\[\bar{F}_\nu = \frac{4\pi h\nu^3}{c^2} \int_1^{x_\mathrm{out}} \frac{x}{\exp \left( \frac{h\nu}{k_B T_\mathrm{eff}(x)} \right) -1} dx\]のように、幾何学的な因子を除いた部分を計算し、その概形を示しています。
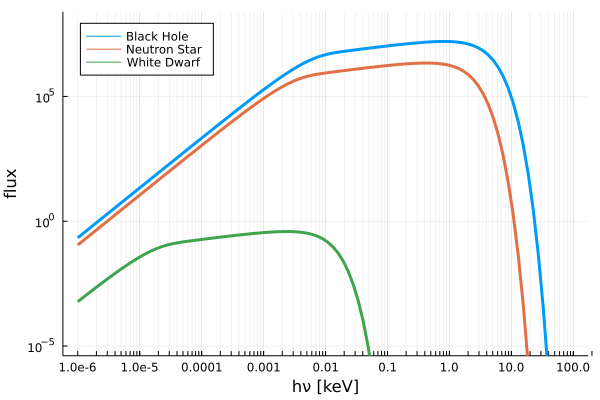
これは各半径(各温度)での黒体放射スペクトルを足し合わせた形をしています。(6)式からわかるように、\(R\)が小さいほど\(T_\mathrm{eff}\)は大きくなります。そのためブラックホールなどのよりコンパクトな天体の方がより高エネルギーのスペクトルの放射を出します。これは\(R\)が小さい場所ほど粘性によるエネルギー散逸\(\epsilon \propto \left( \frac{\partial \Omega_K}{\partial R}\right)^2 \propto R^{-5}\)が大きいことからも類推されます。 黒体放射のスペクトルはプランクの輻射則より、その温度\(T\)からの放射の単位立体角あたりのエネルギー密度は
\[B_\nu(T) = \frac{2h}{c^3} \frac{\nu^3}{\exp \left( \frac{h\nu}{k_B T}\right)-1}\]で与えられます。この関数が最大となる\(\nu_\mathrm{peak}\)を求めてみましょう。両辺を\(\nu\)で微分すると
\[\frac{\partial B_\nu}{\partial \nu} = \frac{2h}{c^3} \frac{3\nu^2( e^{h\nu/k_BT} -1) - \nu^3 e^{h\nu/k_BT} \frac{h}{k_B T}}{(e^{h\nu/k_BT}-1)^2}\]\(x = \frac{h\nu}{k_BT}\)と置くと、上式が0となるのは
\[3(e^x - 1) - xe^x = 0\]この解はニュートン法を用いて数値的に求めることもできますが、解析的にはランベルトの\(W\)関数を用いて
\[x = 3 + W(-3/e^3) \sim 2.82\]と求まります。この値を用いて\(h\nu_\mathrm{peak}\)の典型的な値を見積もってみましょう。
\[h\nu_\mathrm{peak} \simeq 2.82 k_B T \underbrace{=}_{(6)} 2.82 k_B \left\{ \frac{3GM\dot{M}}{8\pi \sigma_\mathrm{SB} R^3} \left( 1-\sqrt{\frac{R_\mathrm{in}}{R}}\right)\right\}^{1/4}\]ここで中心天体は十分コンパクトで、\(R_\mathrm{in} \ll R\)とすると
\[\begin{aligned} h\nu_\mathrm{peak} &= 2.82 k_B \left( \frac{3GM\dot{M}}{8\pi \sigma_\mathrm{SB} R^3} \right)^{1/4} \underbrace{=}_{R_g = \frac{2GM}{c^2}} 2.82 k_B \left( \frac{3\dot{M}}{8\pi \sigma_\mathrm{SB} R^3} \frac{c^2}{2} R_g\right)^{1/4} \\ &= 2.82 k_B \left( \frac{3\dot{M}}{8\pi \sigma_\mathrm{SB}} \frac{c^2}{2} \frac{c^4}{4 G^2 M^2}\right)^{1/4} \left( \frac{R_g}{R}\right)^{3/4} \end{aligned}\]途中、シュバルツシルト半径を用いて整理しました。さらに太陽質量\(M_\odot = 1.989 \times 10^{33} [\mathrm{g}]\)を用いて整理します。
\[\begin{align} h\nu_\mathrm{peak} &= 2.82 k_B \left( \frac{3 \dot{M}}{8\pi \sigma_\mathrm{SB}} \frac{c^2}{2} \frac{c^4}{4G^2 M_\odot^2} \right)^{1/4} \left( \frac{M}{M_\odot}\right)^{-1/2} \left( \frac{R_g}{R}\right)^{3/4} \notag \\ &= 2.82 k_B \left( \frac{3 c^6 \dot{M}}{64\pi \sigma_\mathrm{SB} G^2 M_\odot} \frac{10^{-9}}{1\mathrm{yr}} \right)^{1/4} \left( \frac{\dot{M}}{10^{-9} M_\odot / 1\mathrm{yr}}\right)^{1/4} \left( \frac{M}{M_\odot}\right)^{-1/2} \left( \frac{R_g}{R}\right)^{3/4} \notag \\ &\simeq 7 \left( \frac{\dot{M}}{10^{-9} M_\odot / 1\mathrm{yr}}\right)^{1/4} \left( \frac{M}{M_\odot}\right)^{-1/2} \left( \frac{R_g}{R}\right)^{3/4} \ [\mathrm{keV}] \tag{8} \end{align}\]ブラックホールの場合(\(R_\mathrm{in} = R_g, M=1.4M_\odot, \dot{M} = 10^{-9} M_\odot [\mathrm{yr}^{-1}]\))では降着円盤スペクトルのピークはおよそ7keV程度となります。これは先程の数値計算結果の青線のピーク位置にも大体一致しています。
計算コード
途中で出てきた降着円盤のスペクトルを計算するコードを以下に示します。
include("./const.jl")
using Plots
# compute integrand function
function f(hnu, x, inputs)
M, Mdot, Rin = inputs
T0 = (3*G*M*Mdot/(8*pi*sb*Rin^3))^0.25
Teff = T0 * ((1.0-1.0/sqrt(x))/x^3)^0.25
return x / (exp(hnu/(kb*Teff))-1.0)
end
# compute flux using trapezoidal rule
function calc_flux(xs, hnus, inputs)
fluxs = []
nx = length(xs)
for hnu in hnus
sum = 0.0
for i in 1:nx-1
sum += (xs[i+1]-xs[i]) * (f(hnu, xs[i+1], inputs)+f(hnu, xs[i], inputs)) / 2.0
end
flux = 4 * pi * hnu^3 / (h*c)^2 * sum
push!(fluxs, flux)
end
return fluxs
end
# set range of x (=R/Rin)
xout = 1.0e+4
xin = 1.001
nx = 100000
xs = range(xin, xout, length=nx)
# set range of hnu
hnumax = 2
hnumin = -6
hnnu = 100
hnus = 10.0 .^ range(hnumin, hnumax, length=hnnu) * keV
# set common variables
M = 1.4 * Msun
Mdot = 1.0e-9 * Msun / yr
# set Black Hole Rin
Rin_BH = 2.0 * G * M / c^2
# convert to array
inputs = [M, Mdot, Rin_BH]
# compute flux
fluxs_BH = calc_flux(xs, hnus, inputs)
# corresponds to value lower threshold
fluxs_BH = map(x -> ifelse(x>eps(Float64),x,eps(Float64)), fluxs_BH)
# convert erg to keV
hnus_kev = hnus / keV
##### set xticks for plot start #####
xlab, xval = Float64[], Float64[]
for i in 1:10
for j in hnumin:hnumax
push!(xval, i*10.0^j)
if i == 1
push!(xlab, 10.0^j)
end
end
end
###### set xticks for plot end ######
# make plot for BH
plot(hnus_kev, fluxs_BH, linewidth=3, label="Black Hole", legend=:topleft, xlabel="hν [keV]", ylabel="flux", scale=:log10,
xlims=[hnus[1], hnus[hnnu]]/keV, ylims=[1.0e-5, 1.0e+8], xticks=(xval, xlab))
# set Neutron Star Rin
Rin_NS = 1.0e+6
# convert to array
inputs = [M, Mdot, Rin_NS]
# compute flux
fluxs_NS = calc_flux(xs, hnus, inputs)
# correspond to value lower threshold
fluxs_NS = map(x -> ifelse(x>eps(Float64),x,eps(Float64)), fluxs_NS)
# make plot for NS
plot!(hnus_kev, fluxs_NS, linewidth=3, label="Neutron Star")
# set White Dwarf Rin
Rin_WD = 1.0e+9
# convert to array
inputs = [M, Mdot, Rin_WD]
# compute flux
fluxs_WD = calc_flux(xs, hnus, inputs)
# correspond to value lower threshold
fluxs_WD = map(x -> ifelse(x>eps(Float64),x,eps(Float64)), fluxs_WD)
# make plot for WD
plot!(hnus_kev, fluxs_WD, linewidth=3, label="White Dwarf")
# output plot
savefig("standard_disk_spectrum.png")
最初に読み込んでいるconst.jlには、以下のように物理定数が記述されています。
const G = 6.67e-8
const Msun = 1.99e+33
const yr = 365.0 * 24.0 * 60.0 * 60.0
const sb = 5.67e-5
const c = 3.0e+10
const kb = 1.38e-16
const eV = 1.6e-12
const keV = eV * 10.0^3
const h = 6.63e-27
参考文献
- Koliopanos & Vasilopoulos, 2018, “Accreting, highly magnetized neutron stars at the Eddington limit: a study of the 2016 outburst of SMC X-3”
- 福江純, 和田圭一, 梅村雅之, “宇宙流体力学の基礎”
- 柴田一成, 福江純, 松元亮治, 嶺重慎, “活動する宇宙”
- 小山勝二, 嶺重慎, “ブラックホールと高エネルギー現象”