重力収縮

核融合反応によるエネルギー供給がない場合、恒星は光を発することでエネルギーを失います。 Luminosity (恒星から単位時間に放出されるエネルギー、光度)を\(L\)と書くと、恒星の静水圧平衡状態におけるビリアル定理より

\[L = -\frac{dE_\mathrm{tot}}{dt} = (3\gamma - 4) \frac{dE_\mathrm{i}}{dt} = - \frac{3\gamma - 4}{3(\gamma -1)} \frac{dE_\mathrm{g}}{dt} \tag{1.5.1}\]

という関係が成り立ちます。この式から、核融合反応によるエネルギー供給がない場合、恒星が光を発することで内部エネルギー\(E_\mathrm{i}\)は増大し、重力エネルギー\(E_\mathrm{g}\)は減少する(恒星が収縮する)ことがわかります。理想気体では\(E_\mathrm{i} \propto T\)なので、これは恒星はエネルギーを失うことにより内部の温度が上昇することを意味します。このことから、恒星が「負の比熱を持っている」と形容することもできます。
(1.3.3)式を用いると、\(E_\mathrm{g}\)の時間微分は近似的に

\[\frac{dE_\mathrm{g}}{dt} \simeq -q GM^2 \frac{d}{dt} \left( \frac{1}{R}\right) = q \frac{GM^2}{R^2} \frac{dR}{dt} \tag{1.5.2}\]

と書けます。これを(1.5.1)式に代入すれば

\[L = - q \frac{3\gamma - 4}{3(\gamma - 1)} \frac{GM^2}{R^2} \frac{dR}{dt} \tag{1.5.3}\]

となります。この式は、恒星内部の温度が低く\((T_c \leq 10^7 \mathrm{K})\)、核融合反応が起きないような状態では、恒星は重力収縮\((dR/dt < 0)\)をしなければならないことを示しています。重力収縮によって重力エネルギーが減少し、開放されたエネルギーの一部は内部エネルギー増加に使われ、残りが星の表面まで運ばれて星の光として放出される、というエネルギー収支になっています。

重力収縮による恒星内部の温度変化

重力収縮による恒星内部の温度変化を、相同収縮(homologous contraction)の近似を用いて考察しましょう。静水圧平衡の式(1.2.1)に\(\left( \frac{\partial}{\partial t} \right)_{M_r}\)を作用させると

\[\frac{\partial \dot{P}}{\partial M_r} = 4 \frac{GM_r}{4\pi r^4} \frac{\dot{r}}{r} = - 4 \frac{\dot{r}}{r} \frac{\partial P}{\partial M_r} \tag{1.5.5}\]

を得ます。ここでドットは時間微分(例えば\(\dot{P} \equiv \left(\frac{\partial P}{\partial t}\right)_{M_r}\))を表します。次に、\(\dot{r}/r\)が恒星内部の場所によらず一定である(すなわち中心かranspilerなお距離が同じ比率で変化する)という相同収縮の仮定を導入しましょう。するとこの仮定から

\[\frac{\dot{r}}{r} = \frac{\dot{R}}{R} \tag{1.5.6}\]

を用いると、(1.5.5)式は解析的に積分することができます。

\[\dot{P} = -4 \frac{\dot{R}}{R} P + C\]

恒星表面では\(P = 0, \dot{P} = 0\)より、積分定数は\(C = 0\)とわかります。よって

\[\frac{\dot{P}}{P} = - 4 \frac{\dot{R}}{R} \tag{1.5.7}\]

を得ます。この式は、\(\dot{P} / P\)も場所に依存しない量であることを示しています。
次に、(1.1.15)式を\(t\)で微分しましょう。すると

\[\frac{\partial \dot{r}}{\partial M_r} = \frac{1}{4\pi r^2 \rho} \left( -\frac{2 \dot{r}}{r} - \frac{\dot{\rho}}{\rho} \right) \tag{1.5.8}\]

を得ます。これに相同収縮の仮定(1.5.6)式を用いると

\[\frac{\dot{R}}{R} \frac{\partial r}{\partial M_r} = \frac{\partial r}{\partial M_r} \left( -\frac{2\dot{R}}{R} - \frac{\dot{\rho}}{\rho}\right) \tag{1.5.9}\]

となります。したがって

\[\frac{\dot{\rho}}{\rho} = -\frac{3 \dot{R}}{R} \tag{1.5.10}\]

のようになり、\(\dot{\rho} / \rho\)も場所に依存しない量であることがわかります。比例係数の3は、3次元空間での膨張・収縮では長さの3乗で体積が変化することに対応しています。
温度\(T\)は\(P, \rho\)の関数で表されるので

\[\frac{\dot{T}}{T} = \left( \frac{\partial \ln T}{\partial \ln P}\right)_\rho \frac{\dot{P}}{P} + \left( \frac{\partial \ln T}{\partial \ln \rho}\right)_P \frac{\dot{\rho}}{\rho} = \left[ 4 \left(\frac{\partial \ln T}{\partial \ln P}\right)_\rho + 3 \left(\frac{\partial \ln T}{\partial \ln \rho}\right)_P\right] \left(-\frac{\dot{R}}{R}\right) \tag{1.5.11}\]

のように書かれます。さらに

\[\left(\frac{\partial \ln T}{\partial \ln \rho}\right)_P = - \left(\frac{\partial \ln T}{\partial \ln P}\right)_\rho \left(\frac{\partial \ln P}{\partial \ln \rho}\right)_T \tag{1.5.12}\]

であることを用いると

\[\frac{\dot{T}}{T} = \left[ 4 - 3 \left(\frac{\partial \ln P}{\partial \ln \rho}\right)_T\right] \left(\frac{\partial \ln T}{\partial \ln P}\right)_\rho \left(- \frac{\dot{R}}{R}\right) \tag{1.5.13}\]

と表すことができます。この式は、恒星が重力収縮あるいは膨張で、半径が変化したときに起こる内部温度の変化を表しています。
理想気体では\(P \propto \rho T\)なので、\(\left(\frac{\partial \ln P}{\partial \ln \rho}\right)_T = 1, \left(\frac{\partial \ln T}{\partial \ln P}\right)_\rho = 1\)となります。よって

\[\frac{\dot{T}}{T} = \left(- \frac{\dot{R}}{R}\right) = \frac{\dot{\rho}}{3\rho} \tag{1.5.14}\]

となり、収縮によって星の内部構造が上昇することがわかります。
密度がある程度大きくなると、電子が縮退を始めます。電子が縮退したガスでは、電子の圧力\(P_\mathrm{e}\)がイオンの圧力\(P_\mathrm{I}\)に比べて大きいため

\[P = P_\mathrm{e} + P_\mathrm{I} \simeq P_\mathrm{e} \propto \rho^{5/3} \ \Longrightarrow \ \left(\frac{\partial \ln P}{\partial \ln \rho}\right)_T \simeq \frac{5}{3} \tag{1.5.15}\]

となります。ここでは、ガスは非相対論的に縮退している(\(\rho < 10^6 \mathrm{g}/\mathrm{cm}^3\))として、\(P_\mathrm{e} \propto n_e v p_\mathrm{F} \propto n p_\mathrm{F}^2\)のようにしました。さらに状態数は\(p_\mathrm{F}^3\)に比例するため、\(p_\mathrm{F} \propto n_\mathrm{e}^{1/3}\)となることから、\(P_\mathrm{e} \propto \rho^{5/3}\)となると理解できます。相対論的縮退の場合、\(v \simeq c\)となるため、\(P_\mathrm{e} \propto \rho^{4/3}\)のようになります。また温度依存性は、理想気体と近似できるイオン圧から来るため

\[\left(\frac{\partial \ln P}{\partial \ln T}\right)_\rho = \frac{1}{P} \frac{\partial (P_\mathrm{e} + P_\mathrm{I})}{\partial \ln T}_\rho \simeq \frac{1}{P} \left(\frac{\partial P_\mathrm{I}}{\partial \ln T}\right)_\rho = \frac{P_\mathrm{I}}{P} \underbrace{\left( \frac{\partial \ln P_\mathrm{I}}{\partial \ln T}\right)_\rho}_{理想気体なので1} = \frac{P_\mathrm{I}}{P} \tag{1.5.16}\]

と表されます。したがって

\[\frac{\dot{T}}{T} \simeq - \frac{P}{P_\mathrm{I}} \left( - \frac{\dot{R}}{R}\right) \tag{1.5.17}\]

となります。重力収縮により密度が十分に大きくなり、電子の縮退が強くなると、今度は重力収縮によって温度\(T\)が逆に減少し始めることを示しています。このことは、構成が重力収縮することによって到達することができる最高温度\(T_\mathrm{max}\)が存在することを意味します。密度が大きくないとき、ガスはほぼ理想気体として振る舞い、恒星の内部温度は

\[T \propto \frac{M}{R} \propto \rho^{1/3} M^{2/3} \tag{1.5.18}\]

のように表されるので、ある密度に対する温度は質量が大きいほど高いとわかります。従って、\(T_\mathrm{max}\)は質量が大きいほど高い値を持ちます。密度に対する温度のグラフの概形を下図に示します。

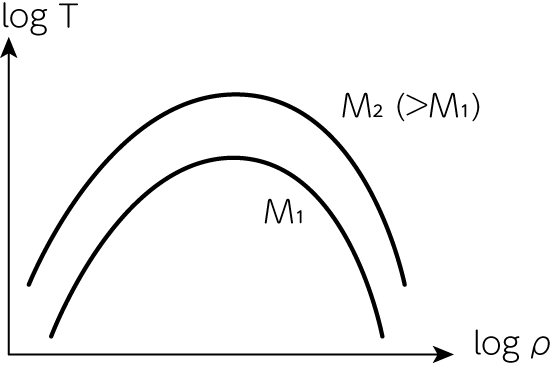
質量が十分小さく(\(M \leq 0.08 M_\odot\))、\(T_\mathrm{max}\)でも中心で水素からヘリウムへの核融合反応によるエネルギーの発生が起こらないような場合、主系列星になることはできません。このような恒星は褐色矮星(brown dwarfs)と呼ばれます。
縮退が強くなると温度が下がるのは、内部エネルギーの増加がフェルミエネルギーの増加に使われてしまうため、と理解することができます。完全に縮退した状態では、圧力は密度のみの関数となるので、恒星の質量と半径が一対一の関係になります。

参考文献

[1] 野本憲一, 佐藤勝彦, 定金晃三, “シリーズ現代の天文学恒星”