Table of contents
シンクロトロン放射
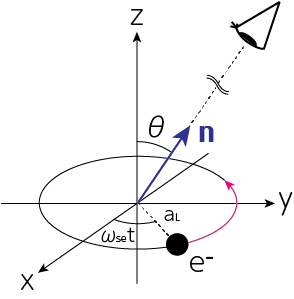
\(z\)軸方向を向いた一様磁場\(B\)中を運動する相対論的電子からの放射の周波数分布の厳密な形を導きましょう。簡単のため、電子は\(xy\)平面内で円運動しているものとします。観測者の視線方向と\(z\)軸方向のなす角を\(\theta\)とすると、軸対称な系なので一般性を失うことなく観測者の視線方向を\(yz\)平面内に設定できます。よって観測者方向の単位ベクトルを\(\mathbf{n} = (0, \sin \theta, \cos \theta)\)のように書くことができます。以下の計算では長時間平均を行うため、部分積分することで出現する振動項の寄与は無視できるとします。
輻射場のフーリエスペクトル
\[\hat{\mathbf{E}}(\mathbf{r}, \omega) = - \frac{i \omega (-e)}{2\pi cR} e^{i\omega \frac{\mathbf{n} \cdot \mathbf{r}}{c}} \int_{T'_1}^{T'_2} \mathbf{n} \times (\mathbf{n} \times \boldsymbol{\beta})e^{i \omega (t'-\frac{\mathbf{r}_0(t') \cdot \mathbf{n}}{c})} dt'\]です。これを具体的に計算するために、今後必要となるものを用意しましょう。電子の円運動の半径はラーモア半径\(a_L = \frac{v_0}{\omega_\mathrm{se}}\)より
\[\mathbf{r}_0 (t') = a_L (\cos \omega_\mathrm{se} t', \sin \omega_\mathrm{se} t', 0)\] \[\boldsymbol{\beta} (t') = \frac{1}{c} \frac{d \mathbf{r}_0(t')}{dt'} = \frac{a_L \omega_\mathrm{se}}{c} (- \sin \omega_\mathrm{se} t ' , \cos \omega_\mathrm{se} t', 0) = \frac{v_0}{c} (- \sin \omega_\mathrm{se} t ' , \cos \omega_\mathrm{se} t', 0)\] \[\begin{align} \mathbf{n} \times (\mathbf{n} \times \boldsymbol{\beta}) &= (\mathbf{n} \cdot \boldsymbol{\beta}) \mathbf{n}- (\mathbf{n} \cdot \mathbf{n}) \boldsymbol{\beta} = (\mathbf{n} \cdot \boldsymbol{\beta}) \mathbf{n}- \boldsymbol{\beta} \notag \\ &= \frac{v_0}{c} \sin \theta \cos \omega_\mathrm{se} t' \left( \begin{array}{c} 0 \\ \sin \theta \\ \cos \theta \end{array} \right) - \frac{v_0}{c} \left( \begin{array}{c} - \sin \omega_\mathrm{se} t' \\ \cos \omega_\mathrm{se} t' \\ 0 \end{array} \right) = \beta \left( \begin{array}{c} \sin \omega_\mathrm{se} t' \\ - \cos^2 \theta \cos \omega_\mathrm{se} t' \\ \sin \theta \cos \theta \cos \omega_\mathrm{se} t' \end{array} \right) \tag{1} \end{align}\]これらから、具体的に成分ごとの計算を行いましょう。まずは\(x\)成分からです。
\[\hat{E}_x (\mathbf{r} , \omega) = \frac{i e \omega \beta }{2\pi c R} e^{i\omega \frac{\mathbf{n} \cdot \mathbf{r}}{c}} \int_{T_1'}^{T_2'} \sin \omega_\mathrm{se} t' e^{i\omega t'} e^{-i \frac{\omega}{c} a_L \sin \theta \sin \omega_\mathrm{se} t' } dt'\]ここで\(\lambda \equiv \frac{\omega}{c} a_L \sin \theta = \frac{\omega \beta}{\omega_\mathrm{se}} \sin \theta\)とおくと
\[\hat{E}_x (\mathbf{r} , \omega) = \frac{i e \omega \beta }{2\pi c R} e^{i\omega \frac{\mathbf{n} \cdot \mathbf{r}}{c}} \int_{T_1'}^{T_2'} \sin \omega_\mathrm{se} t' e^{-i \lambda \sin \omega_\mathrm{se} t' } dt'\] \[\begin{align} e^{i \lambda \sin \omega_\mathrm{se} t' } = \sum_{n=-\infty}^\infty J_n(\lambda) e^{in \omega_\mathrm{se} t'} &\underbrace{\Longrightarrow}_{\omega_\mathrm{se} \rightarrow - \omega_\mathrm{se}} e^{- i \lambda \sin \omega_\mathrm{se} t' } = \sum_{n=-\infty}^\infty J_n(\lambda) e^{- in \omega_\mathrm{se} t'} \notag \\ & \underbrace{\Longrightarrow}_{\times d/d\lambda} - i \sin \omega_\mathrm{se} t' e^{- i\lambda \sin \omega_\mathrm{se} t' } = \sum_{n=-\infty}^\infty J_n' (\lambda) e^{-in \omega_\mathrm{se} t'} \notag \end{align}\]よって
\[\begin{align} \hat{E}_x (\mathbf{r} , \omega) &= - \frac{e \omega \beta }{2\pi c R} e^{i\omega \frac{\mathbf{n} \cdot \mathbf{r}}{c}} \int_{T_1'}^{T_2'} e^{i\omega t'} \sum_{n=-\infty}^\infty J_n' (\lambda) e^{- in \omega_\mathrm{se} t' } dt' = - \frac{e \omega \beta }{2\pi c R} e^{i\omega \frac{\mathbf{n} \cdot \mathbf{r}}{c}} \sum_{n=-\infty}^\infty J_n' (\lambda) \int_{T_1'}^{T_2'} e^{i (\omega - in \omega_{\rm se} ) t' } dt' \notag \\ &= - \frac{e \omega \beta }{2\pi c R} e^{i\omega \frac{\mathbf{n} \cdot \mathbf{r}}{c}} \sum_{n=-\infty}^\infty J_n' (\lambda) \frac{1}{i(\omega - n \omega_\mathrm{se})} \left[ e^{i (\omega - in\omega_\mathrm{se} ) t' } \right]_{T_1'}^{T_2'} \notag \end{align}\]ここで\(\varphi_0 \equiv \omega \frac{\mathbf{n} \cdot \mathbf{r}}{c}\)とし、さらに以降の計算では\(T_1'=-\frac{T'}{2}, T_2'=\frac{T'}{2}\)とすると
\[\begin{align} \hat{E}_x (\mathbf{r} , \omega) &= - \frac{e \omega \beta }{2\pi c R} e^{i\varphi_0}\sum_{n=-\infty}^\infty J_n' (\lambda) \frac{1}{i(\omega - n \omega_\mathrm{se})} 2 i \sin \left\{ (\omega- n \omega_\mathrm{se} ) \frac{T'}{2} \right\} \notag \\ &= - \frac{e \omega \beta }{\pi c R} e^{i\varphi_0} \sum_{n=-\infty}^\infty J_n' (\lambda) \underbrace{\frac{\sin \left\{ (\omega- n \omega_\mathrm{se} ) \frac{T'}{2} \right\} }{(\omega - n \omega_\mathrm{se})\frac{T'}{2}}}_{\mathrm{sinc}} \frac{T'}{2} \notag \\ &= - \frac{e \omega \beta }{2\pi c R} e^{i \varphi_0} T' \sum_{n=-\infty}^\infty J_n' (\lambda) \mathrm{sinc} \left\{ (\omega- n \omega_\mathrm{se} ) \frac{T'}{2} \right\} \tag{2} \end{align}\]同様に\(y\)成分を計算しましょう。
\[\begin{align} \hat{E}_y (\mathbf{r}, \omega) &= - \frac{i e \omega \beta}{2\pi c R} e^{i \varphi_0} \cos^2 \theta \int_{-T'/2}^{T'/2} \cos \omega_\mathrm{se} t' e^{i\omega t'} e^{- i \lambda \sin \omega_\mathrm{se} t' } dt' \notag \\ &= - \frac{i e \omega \beta}{2\pi c R} e^{i \varphi_0} \cos^2 \theta \int_{-T'/2}^{T'/2} e^{i\omega t'} \frac{1}{- i \lambda \omega_\mathrm{se}}\frac{d}{dt'} \left( e^{- i \lambda \sin \omega_\mathrm{se} t' } \right) dt' \notag \\ &= \frac{e \omega \beta}{2\pi c R} \frac{1}{\lambda \omega_\mathrm{se}} e^{i \varphi_0} \cos^2 \theta \left\{ \left[ e^{i\omega t'} e^{- i \lambda \sin \omega_\mathrm{se} t' } \right]_{-T'/2}^{T'/2} - \int_{-T'/2}^{T'/2} i\omega e^{i\omega t'} e^{- i \lambda \sin \omega_\mathrm{se} t' }dt'\right\} \notag \end{align}\]長時間平均をとり、振動項である第一項は無視します。
\[\begin{align} \hat{E}_y (\mathbf{r}, \omega) &= - \frac{e \omega \beta}{2\pi c R} \frac{1}{\lambda \omega_\mathrm{se}} e^{i \varphi_0} \cos^2 \theta \int_{-T'/2}^{T'/2} i\omega e^{i\omega t'} e^{- i \lambda \sin \omega_\mathrm{se} t' }dt' \notag \\ &= - \frac{e \omega \beta}{2\pi c R} \frac{1}{\omega_\mathrm{se} \frac{\omega \beta}{\omega_\mathrm{se}}\sin \theta} e^{i \varphi_0} \cos^2 \theta \int_{-T'/2}^{T'/2} i\omega e^{i\omega t'} \sum_{n=-\infty}^\infty J_n (\lambda) e^{- in\omega_\mathrm{se} t' }dt' \notag \\ &= - \frac{i e \omega}{2\pi c R} \frac{\cos^2 \theta}{\sin \theta} e^{i \varphi_0} \sum_{n=-\infty}^\infty J_n (\lambda) \frac{1}{i (\omega - n \omega_\mathrm{se})} \left[ e^{i(\omega - n\omega_\mathrm{se})t'} \right]_{-T'/2}^{T'/2} \notag \\ &= - \frac{i e \omega}{2\pi c R} \frac{\cos^2 \theta}{\sin \theta} e^{i \varphi_0} \sum_{n=-\infty}^\infty J_n (\lambda) \frac{1}{i (\omega - n \omega_\mathrm{se})} 2i \sin \left\{ (\omega- n \omega_\mathrm{se}) \frac{T'}{2} \right\} \notag \\ &= - \frac{i e \omega}{\pi c R} \frac{\cos^2 \theta}{\sin \theta} e^{i \varphi_0} \sum_{n=-\infty}^\infty J_n (\lambda) \underbrace{\frac{\sin \left\{ (\omega- n \omega_\mathrm{se}) \frac{T'}{2} \right\}}{(\omega - n \omega_\mathrm{se}) \frac{T'}{2}}}_\mathrm{sinc} \frac{T'}{2} \notag \\ &= - \frac{i e \omega}{2 \pi c R} \frac{\cos^2 \theta}{\sin \theta} e^{i \varphi_0} T' \sum_{n=-\infty}^\infty J_n (\lambda) \mathrm{sinc} \left\{ (\omega- n \omega_\mathrm{se}) \frac{T'}{2} \right\} \tag{3} \end{align}\]最後に\(z\)成分の計算を行いますが、これは(1)式の\(y, z\)成分を見比べてみると、その違いは\(\theta\)依存性のみであることがわかります。よって(3)式で\(- \cos^2 \theta \rightarrow \sin \theta \cos \theta\)に置き換えたものが\(\hat{E}_z(\mathbf{r}, \omega)\)となります。
\[\therefore \ \hat{E}_z (\mathbf{r}, \omega) = \frac{i e \omega}{2 \pi c R} \cos \theta e^{i \varphi_0} T' \sum_{n=-\infty}^\infty J_n (\lambda) {\rm sinc} \left\{ (\omega- n \omega_\mathrm{se}) \frac{T'}{2} \right\} \tag{4}\]
単位立体角あたりの放射強度
視線方向と磁場が作る平面内、及びその平面に垂直な方向に偏光した成分の単位時間・単位周波数・単位立体角あたりの放射強度を計算しましょう。これらは今の問題設定から、それぞれ以下のように与えられます。
\[\frac{d W_\perp}{d\omega d\Omega dt'} = \frac{c R^2}{T'} \left| {\hat E}_x \right|^2\] \[\frac{d W_{\parallel}}{d\omega d\Omega dt'} = \frac{c R^2}{T'} \left( \left| {\hat E}_y \right|^2 + \left| {\hat E}_z \right|^2 \right)\](2)式より
\[\frac{d W_{\perp}}{d\omega d\Omega dt'} = \frac{e^2 \beta^2 }{4\pi^2 c} T' \omega^2 \left( \sum_{n=-\infty}^\infty J_n' (\lambda) \mathrm{sinc} \left\{ (\omega - n \omega_\mathrm{se}) \frac{T'}{2} \right\}\right) \left( \sum_{m=-\infty}^\infty J_m' (\lambda) \mathrm{sinc} \left\{ (\omega - m \omega_\mathrm{se}) \frac{T'}{2} \right\}\right)\]この式を角周波数で積分します。ここで積分時間\(T'\)は観測時間であり、長時間平均していたことを思い出しましょう。すると\(T' \rightarrow \infty\)より、2つのsinc関数は\(\omega \simeq n \omega_\mathrm{se}, \omega \simeq m \omega_\mathrm{se}\)以外の\(\omega\)でほぼ0であるような、デルタ関数的な振る舞いをしていると考えて良いでしょう。よって上式を\(\omega\)で積分するときには、異なる次数\(n, m\)が掛け合わさった項は0とします。
\[\frac{d W_{\perp}}{d\Omega dt'} = \lim_{T' \rightarrow \infty} \frac{e^2 \beta^2}{4\pi^2 c} T' \int_0^\infty \omega^2 \sum_{n=-\infty}^\infty J_n' (\lambda)^2 \mathrm{sinc}^2 \left\{ (\omega - n \omega_\mathrm{se}) \frac{T'}{2} \right\} d\omega\]この積分を計算するために、sincの2乗の積分公式
\[\int_{-\infty}^\infty {\rm sinc}^2 x \ dx = \pi\]を考えます。\(x = \frac{\omega - n\omega_\mathrm{se}}{2} T' \ (dx = \frac{1}{2} T'd\omega)\)と置換すると
\[\int_{-\infty}^\infty T' \mathrm{sinc}^2 \left\{ (\omega - n \omega_\mathrm{se}) \frac{T'}{2} \right\} d\omega =2 \pi\]です。先ほどの議論から\(T' \rightarrow \infty\)では、このsinc関数はデルタ関数と近似して良いとして
\[\lim_{T' \rightarrow \infty}T' \mathrm{sinc}^2 \left\{ (\omega - n \omega_\mathrm{se}) \frac{T'}{2} \right\} = 2\pi \delta (\omega - n \omega_\mathrm{se})\]以上より
\[\frac{d W_\perp}{d\Omega dt'} = \frac{e^2 \beta^2}{2\pi c} \int_{0}^\infty \sum_{n=-\infty}^\infty \omega^2 J_n'(\lambda)^2 \delta (\omega- n \omega_\mathrm{se}) d\omega\]\(\omega_n \equiv n \omega_\mathrm{se}, \lambda_n \equiv \lambda(\omega=\omega_n)=\frac{n \omega_\mathrm{se} \beta}{\omega_\mathrm{se}} \sin \theta = n \beta \sin \theta\)と定義します。さらに\(\omega>0\)より、\(\sum_{n= -\infty}^{\infty}\)において、\(n\)が負の部分の和は寄与しない(0になる)ことを用いると
\[\frac{d W_\perp}{d\Omega dt'} = \frac{e^2 \beta^2}{2\pi c} \sum_{n=0}^\infty \omega_n^2 J_n'(\lambda_n)^2 \tag{5}\]と求まります。同様の計算を、もう一つにも行っていきましょう。
\[\begin{align} \frac{dW_\parallel}{d\Omega dt'} &= \lim_{T' \rightarrow \infty} \frac{e^2 }{4\pi^2 c} \int_0^\infty \omega^2 \left[ \frac{\cos^4 \theta}{\sin^2 \theta} T' \left(\sum_{n=-\infty}^\infty J_n (\lambda) \mathrm{sinc} \left\{ (\omega- \omega_n) \frac{T'}{2} \right\} \right)^2 \right. \notag \\ & \quad \left. + \cos^2 \theta \ T' \left( \sum_{n=-\infty}^\infty J_n (\lambda) \mathrm{sinc} \left\{ (\omega- \omega_n) \frac{T'}{2} \right\} \right)^2 \right] d\omega \notag \\ &=\lim_{T' \rightarrow \infty} \frac{e^2}{4\pi^2 c} \frac{\cos^2 \theta}{\sin^2 \theta} \int_0^\infty \omega^2 T' \left(\sum_{n=-\infty}^\infty J_n (\lambda) \mathrm{sinc} \left\{ (\omega- \omega_n) \frac{T'}{2} \right\} \right)^2 d\omega \notag \\ &= \lim_{T' \rightarrow \infty} \frac{e^2}{4\pi^2 c} \frac{\cos^2 \theta}{\sin^2 \theta} \int_0^\infty \omega^2 T' \sum_{n=-\infty}^\infty J_n (\lambda)^2 \mathrm{sinc}^2 \left\{ (\omega- \omega_n) \frac{T'}{2} \right\} d\omega \notag \\ &= \frac{e^2}{4\pi^2 c} \frac{\cos^2 \theta}{\sin^2 \theta} \int_0^\infty \underbrace{\sum_{n=-\infty}^\infty}_{=\sum_{n=0}^\infty} \omega^2 J_n (\lambda)^2 \underbrace{\lim_{T' \rightarrow \infty} T' \mathrm{sinc}^2 \left\{ (\omega- \omega_n) \frac{T'}{2} \right\}}_{=2\pi \delta (\omega- \omega_n)} d\omega \notag \\ &= \frac{e^2}{2\pi c} \frac{\cos^2 \theta}{\sin^2 \theta} \sum_{n=0}^\infty \omega_n^2 J_n (\lambda_n)^2 \tag{6} \end{align}\]全放射強度
(5), (6)式より
\[\begin{align} \frac{d W}{dt'} &= \frac{d W_\perp}{dt'}+ \frac{d W_{\parallel}}{dt'} = \frac{e^2}{2\pi c} \int_0^{2\pi} d\varphi \int_0^\pi \sum_{n=0}^\infty \left\{ \beta^2 \omega_n^2 ( J_n'(\lambda_n) )^2 + \frac{\cos^2 \theta}{\sin^2 \theta} \omega_n^2 (J_n(\lambda_n))^2\right\} \sin \theta \ d\theta \notag \\ &= \frac{e^2}{c} \sum_{n=0}^\infty \omega_n^2 \int_0^\pi \left\{ \beta^2 ( J_n'(\lambda_n) )^2 + \frac{\cos^2 \theta}{\sin^2 \theta} (J_n(\lambda_n))^2\right\} \sin \theta \ d\theta \notag \end{align}\] \[\frac{n}{\lambda_n} J_n (\lambda_n) = \frac{1}{2} (J_{n-1} (\lambda_n) + J_{n+1} (\lambda_n) ), \ J_n' (\lambda_n) = \frac{1}{2} (J_{n-1}(\lambda_n)- J_{n+1} (\lambda_n))\]を用いて整理を行いましょう。
\[\begin{align} \frac{dW}{dt'} &= \frac{e^2}{c} \sum_{n=0}^\infty \omega_n^2 \int_0^\pi \left\{ \frac{\beta^2}{4} (J_{n-1}^2 - 2 J_{n-1} J_{n+1} + J_{n+1}^2) + \left( \frac{1}{\sin^2 \theta} -1 \right)J_n^2\right\} \sin \theta \ d\theta \notag \\ &= \frac{e^2}{c} \sum_{n=0}^\infty \omega_n^2 \int_0^\pi \left\{ \frac{\beta^2}{4} (J_{n-1}^2 - 2 J_{n-1} J_{n+1} + J_{n+1}^2) + \left( \frac{n^2 \beta^2}{\lambda_n^2} -1 \right)J_n^2\right\} \sin \theta \ d\theta \notag \\ &= \frac{e^2}{c} \sum_{n=0}^\infty \omega_n^2 \int_0^\pi \left\{ \frac{\beta^2}{4} (J_{n-1}^2 - 2 J_{n-1} J_{n+1} + J_{n+1}^2) + \frac{\beta^2}{4}(J_{n-1}^2+ 2 J_{n-1}J_{n+1} + J_{n+1}^2)-J_n^2 \right\} \sin \theta \ d\theta \notag \\ &= \frac{e^2}{c} \sum_{n=0}^\infty \omega_n^2 \int_0^\pi \left\{ \frac{\beta^2}{2} (J_{n-1}^2 + J_{n+1}^2) -J_n^2 \right\} \sin \theta \ d\theta \notag \\ &= \frac{e^2}{c} \sum_{n=0}^\infty \omega_n^2 \int_0^\pi \left\{ \frac{\beta^2}{2} (J_{n-1}^2 - 2 J_n^2 + J_{n+1}^2) + (\beta^2-1) J_n^2 \right\} \sin \theta \ d\theta \notag \end{align}\]ここで
\[\int_{\pi/2}^\pi J_n^2(\lambda_n) \sin \theta \ d\theta \underbrace{=}_{\theta \rightarrow \pi - \Theta} \int_{\pi/2}^0 J_n^2 (n\beta \sin(\pi- \Theta)) \sin (\pi - \Theta) (- d\Theta) = \int_0^{\pi/2} J_n^2 (n\beta \sin \Theta) \sin \Theta \ d\Theta\]より
\[\frac{dW}{dt'} = \frac{2 e^2}{c} \sum_{n=0}^\infty \omega_n^2 \int_0^{\pi/2} \left\{ \frac{\beta^2}{2} (J_{n-1}^2 - 2 J_n^2 + J_{n+1}^2) + (\beta^2 -1)J_n^2 \right\} \sin \theta \ d\theta\]さらにベッセル関数の積分公式
\[\int_0^{\pi/2} J_n^2 (z \sin \theta) \sin \theta \ d\theta = \frac{1}{2z} \int_0^{2z} J_{2n}(t) dt \ \Longrightarrow \ \int_0^{\pi/2} J_n^2 (n \beta \sin \theta) \sin \theta \ d \theta = \frac{1}{2n \beta} \int_0^{2n\beta} J_{2n} (t) dt\]より
\[\begin{align} \frac{dW}{dt'} &= \frac{e^2}{c\beta} \sum_{n=0}^\infty \frac{\omega_n^2}{n} \left\{ \frac{\beta^2}{2} \int_0^{2n\beta} (J_{2(n-1)} - 2 J_{2n} + J_{2(n+1)} )dt + (\beta^2 -1) \int_0^{2n\beta} J_{2n} \ dt \right\} \notag \\ &= \frac{e^2}{c\beta} \sum_{n=0}^\infty \frac{\omega_n^2}{n} \left\{ \frac{\beta^2}{2} \int_0^{2n\beta} [ ( J_{(2n-1)-1} - J_{(2n-1)+1}) - (J_{(2n+1)-1} - J_{(2n+1)+1}) ]dt + (\beta^2 -1) \int_0^{2n\beta} J_{2n} \ dt \right\} \notag \\ &= \frac{e^2}{c\beta} \sum_{n=0}^\infty \frac{\omega_n^2}{n} \left\{ \frac{\beta^2}{2} \int_0^{2n\beta} 2( J_{2n-1}' - J_{2n+1}' )dt + (\beta^2 -1) \int_0^{2n\beta} J_{2n} \ dt \right\} \notag \\ &= \frac{e^2}{c\beta} \sum_{n=0}^\infty \frac{\omega_n^2}{n} \left\{ \beta^2 [J_{2n-1} - J_{2n+1}]_0^{2n \beta} + (\beta^2 -1) \int_0^{2n\beta} J_{2n} \ dt \right\} \notag \\ &= \frac{e^2}{c\beta} \sum_{n=0}^\infty \frac{\omega_n^2}{n} \left\{ \beta^2 [\{ J_{2n-1}(2n\beta) - J_{2n+1}(2n\beta) \} - \{ J_{2n-1}(0) - J_{2n+1}(0) \} ] + (\beta^2 -1) \int_0^{2n\beta} J_{2n} \ dt \right\} \notag \\ &= \frac{e^2}{c\beta} \sum_{n=0}^\infty \frac{\omega_n^2}{n} \left\{ 2 \beta^2 [\{J_{2n}'(2n\beta) - J_{2n}'(0) \} ] + (\beta^2 -1) \int_0^{2n\beta} J_{2n} \ dt \right\} \notag \end{align}\]ここで
\[\begin{align} J_n' (z) &= \frac{1}{\pi} \int_0^\pi \frac{d}{dz} \cos (n \varphi - z \sin \varphi) \ d\varphi = \frac{1}{\pi} \int_0^\pi \sin \varphi \sin (n \varphi - z \sin \varphi) \ d\varphi \notag \\ \underbrace{\Longrightarrow}_{z=0} J_n'(0) &= \frac{1}{\pi} \int_0^\pi \sin \varphi \sin n \varphi \ d\varphi = \frac{1}{2 \pi} \int_0^\pi \{ \cos(n\varphi- \varphi) - \cos (n \varphi + \varphi)\} d\varphi \notag \\ &=\frac{1}{2\pi} \left[ \frac{1}{n-1} \sin (n-1)\varphi - \frac{1}{n+1} \sin (n+1) \varphi\right]_0^\pi = 0 \notag \end{align}\]より
\[\begin{align} \frac{dW}{dt'} &= \frac{e^2}{c\beta} \sum_{n=0}^\infty \frac{\omega_n^2}{n} \{ 2 \beta^2J_{2n}'(2n\beta) + (\beta^2 -1) \int_0^{2n\beta} J_{2n} \ dt \} \notag \\ &= \frac{e^2 \omega_{\rm se}^2}{c\beta} \sum_{n=0}^\infty n \{ 2 \beta^2J_{2n}'(2n\beta) + (\beta^2 -1) \int_0^{2n\beta} J_{2n}(t) dt \} \notag \\ &\underbrace{=}_{t=2n\xi} \frac{2e^2 \omega_{\rm se}^2}{c\beta} \sum_{n=0}^\infty n \{\beta^2J_{2n}'(2n\beta) - n (1- \beta^2) \int_0^\beta J_{2n}(2n\xi)d\xi \} \tag{7} \end{align}\]
単位角周波数あたりの放射強度
相対論的ビーミングによる観測される放射スペクトル変化から、磁場によって円運動する電子からの輻射スペクトルは
\[0 < \nu = \frac{\omega}{2\pi} < \gamma^2 \omega_{ce} = \gamma^3 \omega_\mathrm{se}\]の広がりを持ちます。よって以下では\(\omega_n = n \omega_\mathrm{se}\)から、\(n \simeq \gamma^3 \gg 1\)とします。さらに
\[n =\frac{\omega}{\omega_{\rm se}} \ \Longrightarrow \ \sum_{n=0}^\infty \rightarrow \int_0^\infty dn = \int_0^\infty \frac{d\omega}{\omega_\mathrm{se}}\]のように和の記号を積分で置き換えます。すると
\[\frac{dW}{dt'} = \frac{2e^2 \omega_\mathrm{se}^2}{c\beta} \int_0^\infty \frac{d\omega}{\omega_\mathrm{se}} \frac{\omega}{\omega_\mathrm{se}} \left\{\beta^2J_{2n}'(2n\beta) + \frac{\omega}{\omega_\mathrm{se}} (\beta^2 -1) \int_0^\beta J_{2n}(2n\xi)d\xi \right\}\]です。ここにベッセル関数の近似式を用いると
\[\begin{align} J_{2n}(2n\xi) &= \frac{1}{\pi} \int_0^\pi \cos (2n \varphi - 2n \xi \sin \varphi) d\varphi = \frac{1}{\pi} \int_0^\pi \cos \{ 2n (\varphi -\xi \sin \varphi)\} d\varphi \notag \\ &\simeq \frac{1}{\pi} \int_0^\infty \cos \left\{ 2n \left( \frac{1- \xi^2}{2} \varphi + \frac{\varphi^3}{6} \right)\right\} d\varphi \notag \end{align}\]さらにエアリー関数より
\[\begin{align} \Phi (n^{2/3}(1-\xi^2)) &= \frac{1}{\sqrt{\pi}} \int_0^\infty \cos \left[ \frac{\varphi^3}{3} + \varphi n^{2/3}(1-\xi^2) \right] d \varphi \underbrace{=}_{\varphi=n^{1/3}\phi} \frac{n^{1/3}}{\sqrt{\pi}} \int_0^\infty \cos \left[ \frac{\phi^3}{3} n + \phi n (1-\xi^2) \right] d \phi \notag \\ &= \frac{n^{1/3}}{\sqrt{\pi}} \int_0^\infty \cos \left[ 2n \left\{ \frac{\phi^3}{6} + \phi \frac{(1-\xi^2)}{2} \right\} \right] d \phi = \sqrt{\pi} n^{1/3} J_{2n} (2n\xi) \notag \\ &\Longrightarrow \ J_{2n} (2n\xi) = \frac{1}{\sqrt{\pi} n^{1/3}} \Phi (n^{2/3}(1-\xi^2)) \notag \end{align}\]です。さらにここから
\[\begin{align} J_{2n}'(2n\xi) &= \frac{d}{d(2n\xi)} J_{2n}(2n\xi) = \frac{1}{2 \sqrt{\pi} n^{4/3}} \frac{d}{d\xi} \Phi (n^{2/3}(1-\xi^2)) = \frac{1}{2 \sqrt{\pi} n^{4/3}} \frac{d(n^{2/3}(1-\xi^2))}{d\xi} \Phi' (n^{2/3}(1-\xi^2)) \notag \\ &= \frac{1}{2 \sqrt{\pi} n^{4/3}} (-2n^{2/3}\xi) \Phi' (n^{2/3}(1-\xi^2)) = - \frac{ \xi}{\sqrt{\pi} n^{2/3}} \Phi' (n^{2/3}(1-\xi^2)) \notag \end{align}\]と計算されます。よって
\[\frac{dW}{d\omega dt'} = \frac{2e^2 \omega_\mathrm{se}^2}{c\beta} \left\{ \frac{\omega}{\omega_\mathrm{se}^2} \beta^2 \left( - \frac{\beta}{\sqrt{\pi} n^{2/3}} \Phi' (n^{2/3}(1-\beta^2)) \right) - \frac{\omega^2}{\omega_\mathrm{se}^3} (1- \beta^2)\int_0^\beta \frac{1}{\sqrt{\pi} n^{1/3}} \Phi (n^{2/3}(1-\xi^2)) d\xi \right\}\]ここで\(u=\left(\frac{\omega}{\omega_{\rm se}} \right)^{2/3} (1- \xi^2)\)と置換すると\(du = -2 \xi \left( \frac{\omega}{\omega_{\rm se}} \right)^{2/3}d \xi\)、\(\xi = 0 \rightarrow \beta\)のとき\(u= \left( \frac{\omega}{\omega_{\rm se}} \right)^{2/3} \rightarrow \left( \frac{\omega}{\omega_{\rm se}} \right)^{2/3} (1- \beta^2) \equiv u_0\)となりますが、今\(\omega \simeq \gamma^3 \omega_\mathrm{se} \gg 1 \ (\gamma \gg 1)\)より\(\left( \frac{\omega}{\omega_\mathrm{se}} \right)^{2/3} \sim \infty\)としてよいでしょう(相対論的電子の運動より\(\beta \sim 1, \xi \sim 1\)から\(u_0\)は有限値です)。\(\omega=n \omega_\mathrm{se}\)であることを思い出せば
\[\begin{align} \frac{dW}{d\omega dt'} &= \frac{2e^2 \omega_\mathrm{se}^2}{c\beta} \left\{ - \frac{\omega}{\omega_\mathrm{se}^2} \beta^2 \frac{\beta}{\sqrt{\pi}} \left( \frac{\omega_\mathrm{se}}{\omega}\right)^{2/3} \Phi' (u_0) - \frac{\omega^2}{\omega_\mathrm{se}^3} \frac{1-\beta^2}{\sqrt{\pi}} \left( \frac{\omega_\mathrm{se}}{\omega} \right)^{1/3}\int_\infty^{u_0} \Phi (u) \left( - \frac{1}{2\xi} \left( \frac{\omega_\mathrm{se}}{\omega}\right)^{2/3}\right) du \right\} \notag \\ &\underbrace{\simeq}_{\beta \sim 1, \xi \sim 1} - \frac{2e^2 \omega_\mathrm{se}}{c \sqrt{\pi}} \left\{ \left( \frac{\omega}{\omega_\mathrm{se}} \right)^{1/3} \Phi' (u_0) + \frac{\omega}{\omega_\mathrm{se}} \frac{1-\beta^2}{2} \int_{u_0}^\infty \Phi (u) du \right\} \notag \end{align}\]です。シンクロトロン振動数は\(\omega_\mathrm{se}=\frac{eB}{\gamma m_e c} = \frac{eB}{m_e c} (1-\beta^2)^{1/2}\)より
\[\begin{align} \frac{dW}{d\omega dt'} &\simeq - \frac{2e^3 B}{m_e c^2 \sqrt{\pi}} \{ \underbrace{ \left( \frac{\omega}{\omega_\mathrm{se}} \right)^{1/3} (1-\beta^2)^{1/2}}_{=u_0^{1/2}}\Phi' (u_0) + \underbrace{\frac{\omega}{\omega_\mathrm{se}} (1-\beta^2)^{3/2}}_{=u_0^{3/2}} \frac{1}{2} \int_{u_0}^\infty \Phi (u) du \} \notag \\ &= - \frac{2e^3 B}{m_e c^2 \sqrt{\pi}} \sqrt{u_0} \left( \Phi' (u_0) + \frac{u_0}{2} \int_{u_0}^\infty \Phi (u) du \right) \notag \end{align}\] \[\Phi (u) = \sqrt{\frac{u}{3\pi}}K_{1/3} \left( \frac{2}{3} u^{3/2}\right), \quad \Phi'(u) = - \frac{u}{\sqrt{3\pi}} K_{2/3} \left( \frac{2}{3} u^{3/2} \right)\]より、これらを用いると
\[\frac{dW}{d\omega dt'} = - \frac{2e^3 B}{m_e c^2 \sqrt{\pi}} \sqrt{u_0} \left\{ - \frac{u_0}{\sqrt{3\pi}} K_{2/3} \left( \frac{2}{3} u_0^{3/2} \right) + \frac{u_0}{2} \int_{u_0}^\infty \sqrt{\frac{u}{3\pi}}K_{1/3} \left( \frac{2}{3} u^{3/2}\right) du \right\}\]ここで\(\chi = \frac{2}{3} u^{3/2}\)とおくと、\(d\chi = \frac{2}{3} \cdot \frac{3}{2} u^{1/2} du = u^{1/2} du\)、また\(\chi_0 = \frac{2}{3} u_0^{3/2}\)とすると
\[\begin{align} \frac{dW}{d\omega dt'} &= - \frac{2e^3 B}{m_e c^2 \sqrt{\pi}} \frac{1}{\sqrt{3\pi}} \frac{3}{2} \chi_0 \left( - K_{2/3} ( \chi_0 ) + \frac{1}{2} \int_{\chi_0}^\infty K_{1/3} (\chi ) d\chi \right) \notag \\ &= - \frac{\sqrt{3} e^3 B}{m_e c^2 \pi} \chi_0 \left( - K_{2/3} ( \chi_0 ) + \frac{1}{2} \int_{\chi_0}^\infty K_{1/3} (\chi ) d\chi \right) \notag \end{align}\]ここで修正ベッセル関数より
\[\lim_{z\rightarrow \infty} K_{2/3} (z) = \int_0^\infty e^{-z \cosh t} \cosh \frac{2}{3} t \ dt = 0 \ \Longrightarrow \ K_{2/3}(\chi_0) = \int_\infty^{\chi_0} K_{2/3}'(\chi) d \chi\]と書けるので
\[\frac{dW}{d\omega dt'} = - \frac{\sqrt{3} e^3 B}{m_e c^2 \pi} \chi_0 \left( \int_{\chi_0}^\infty K_{2/3}'(\chi) d \chi + \frac{1}{2} \int_{\chi_0}^\infty K_{1/3} (\chi ) d\chi \right)\]となります。さらには
\[K_{2/3}' = - \frac{1}{2} (K_{-1/3} + K_{5/3}) = - \frac{1}{2} (K_{1/3} + K_{5/3})\]という漸化式より
\[\frac{dW}{d\omega dt'} = \frac{\sqrt{3} e^3 B}{2 m_e c^2 \pi} \chi_0 \int_{\chi_0}^\infty K_{5/3} (\chi ) d\chi = \frac{\sqrt{3} e^3 B}{2 m_e c^2 \pi} F(\chi_0) \quad \left( F(\chi_0) \equiv \chi_0 \int_{\chi_0}^\infty K_{5/3} (\chi ) d\chi \right) \tag{8}\]と求まります。これが電子1つが磁場の周りを円運動するときに発生する、シンクロトロン放射のスペクトルです。
関数\(F\)の振る舞い
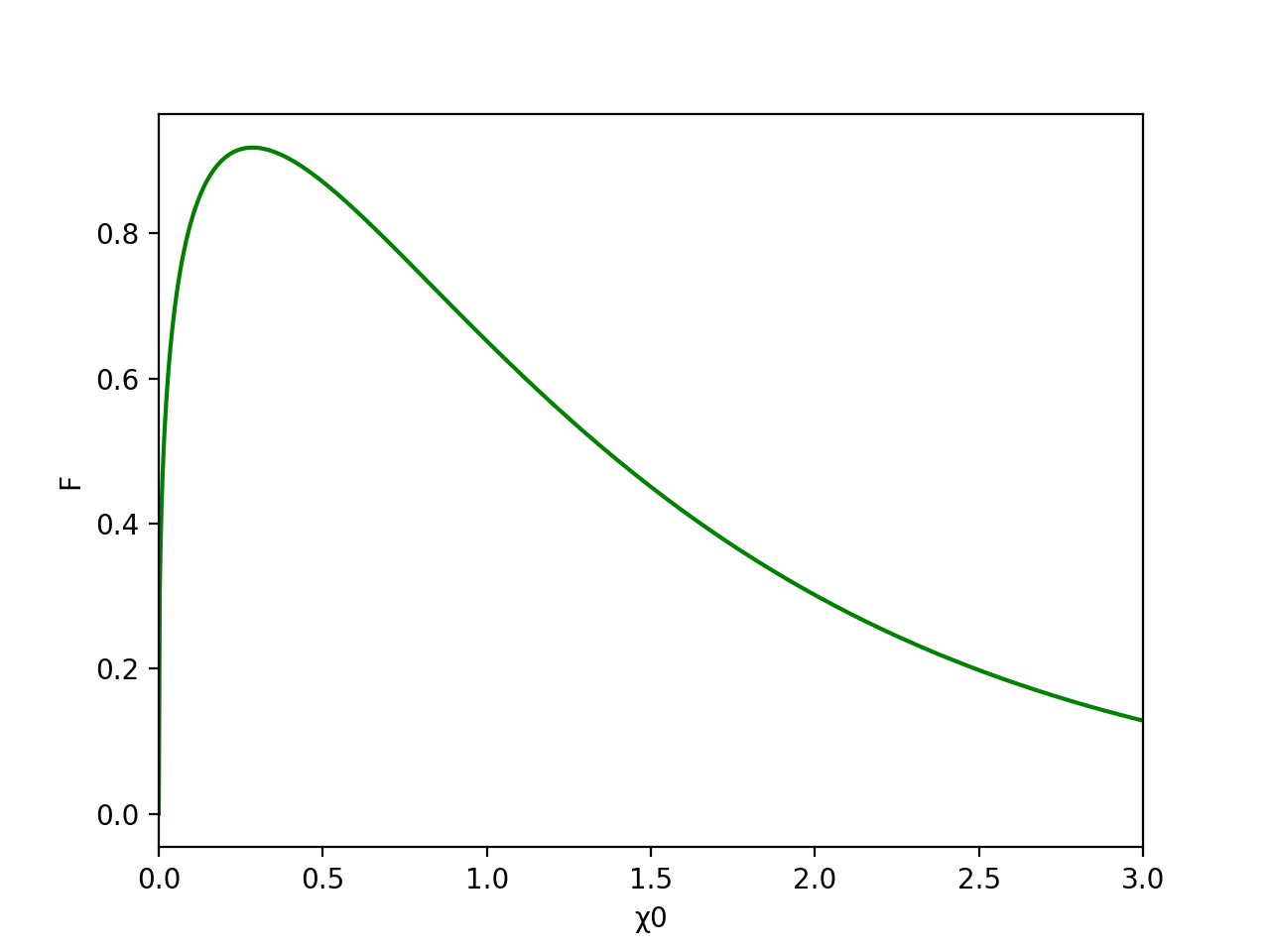
(8)式で現れた関数\(F(\chi_0)\)の振る舞いを数値的に示してみましょう。数値積分を行うと、以下のようなグラフを得ます。
また両対数グラフで表示すると以下のようになります。
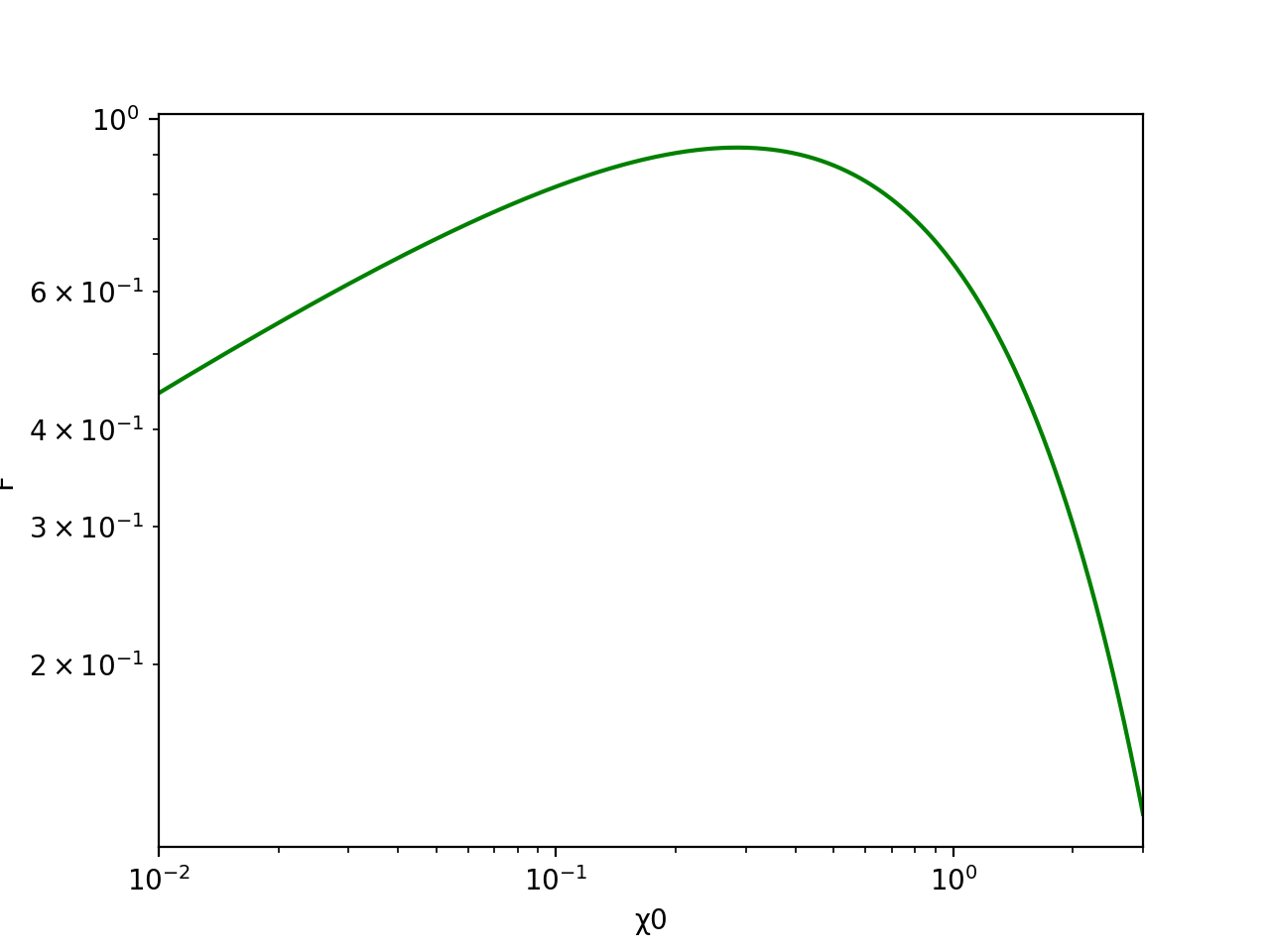
グラフからわかるように、\(\chi_0 \sim 0.29\)で最大値をとるような関数となります。
またここでは証明を行いません(というより証明できませんでした)が、漸近的な振る舞いは以下のようになります。
べき乗の電子分布からの放射スペクトル
今までの計算は1個の電子からのシンクロトロン放射スペクトルでした。以下では電子のエネルギー分布が
\[N (\gamma) d\gamma = N_0 \left( \frac{\gamma}{\gamma_0} \right)^{-p} \frac{d\gamma}{\gamma_0} \tag{9}\]のようにべき乗で与えられる場合を考えましょう。ただし、電子の速度分布は等方的であるとします。興味のある量は全ての電子からの放射の重ね合わせの結果、ある特定の視線方向\(\mathbf{n}\)で観測される単位立体角あたりの放射強度です。このためには様々なピッチ角\(\alpha\)の電子が\(\mathbf{n}\)の方向に放射する輻射場を重ね合わせる必要があります。電子の空間分布がランダムで密度が十分希薄なら、各電子からの放射の重ね合わせは非可干渉な重ね合わせとなります。よって、各電子が\(\mathbf{n}\)の方向に放射する放射強度を足し合わせれば良いでしょう。以下では簡単のため、視線方向が\(y\)軸方向と一致する場合、すなわち\(\theta=\pi/2\)の場合をとりあげます。このとき、相対論的ビーミングの議論から、ピッチ角が\(\pi/2\)を中心に\(\pm 1/\gamma\)の狭い範囲の電子からの寄与のみ考慮すれば十分です。したがって、下図のようにピッチ角が\(\alpha_0\)の電子の\(\theta=\pi/2\)方向への寄与を、同じエネルギーを持つピッチ角が\(\pi/2\)(\(xy\)平面内を円運動するのと同じ)の電子から\(\theta=\pi-\alpha_0\)方向への放射強度と近似することができます。
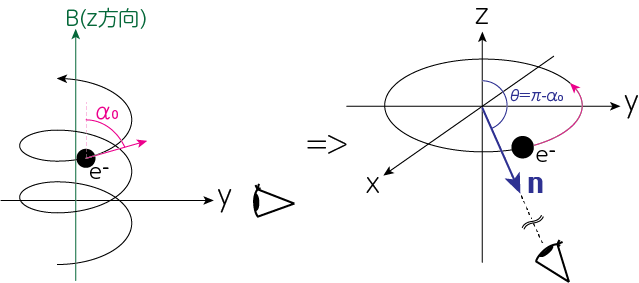
視線方向が任意の\(\theta\)の場合には、これまで得られた結果の中の磁場\(B\)を\(B_\perp=B\sin \theta\)で置き換えることで得ることができます。以上の議論から(8)式に(9)式をかけたものを\(\gamma\)で積分します。そのときに\(B \rightarrow B_\perp\)で置き換え、全立体角\(4\pi\)で割ると
\[P_e (\omega, \mathbf{n}) = \frac{\sqrt{3} e^3 B_\perp}{8\pi^2 m_e c^2} N_0 \gamma_0^{p-1} \int_0^\infty \gamma^{-p} F(\chi_0) d\gamma\]\(\chi_0\)の定義から
\[\begin{align} &\chi_0 = \frac{2}{3} u_0^{3/2} = \frac{2}{3} \frac{\omega}{\omega_\mathrm{se}} \gamma^{-3} = \frac{2m_ec\omega}{3eB_\perp} \gamma^{-2} \ \Longrightarrow \ \gamma = \left( \frac{2m_ec\omega}{3eB_\perp}\right)^{1/2} \chi_0^{-\frac{1}{2}} \notag \\ &\Longrightarrow \ d\gamma = \left( \frac{2m_ec\omega}{3eB_\perp} \right)^{1/2} \left( - \frac{1}{2}\right) \chi_0^{-\frac{3}{2}} \ d\chi_0 \notag \end{align}\]\(\gamma = 0 \rightarrow \infty\)のとき、\(\chi_0 = \infty \rightarrow 0\)より
\[\begin{align} P_e (\omega, \mathbf{n}) &= \frac{\sqrt{3} e^3 B_\perp}{8\pi^2 m_e c^2} N_0 \gamma_0^{p-1} \int_\infty^0 \left( \frac{2m_ec \omega}{3eB}\right)^{1/2} \left( -\frac{1}{2}\right) \chi_0^{-\frac{3}{2}} \left( \frac{2m_ec \omega}{3eB_\perp}\right)^{-\frac{p}{2}} \chi_0^{p/2} F (\chi_0) d\chi_0 \notag \\ &= \frac{\sqrt{3} e^3 B_\perp}{8\pi^2 m_e c^2} \frac{N_0}{2} \gamma_0^{p-1} \left( \frac{2m_ec \omega}{3eB_\perp}\right)^{-\frac{p-1}{2}} \int_0^\infty \chi_0^{\frac{p-3}{2}} F (\chi_0) d\chi_0 \notag \end{align}\]ここで以下の公式を用います。
\[\int_0^\infty x^\mu F(x) dx = \frac{2^{\mu + 1}}{\mu + 2} \Gamma \left( \frac{\mu}{2} + \frac{7}{3} \right) \Gamma \left( \frac{\mu}{2} + \frac{2}{3} \right)\]これを用いて整理すると
\[\begin{align} P_e (\omega, \mathbf{n}) &= \frac{\sqrt{3} e^3 B_\perp}{8\pi^2 m_e c^2} \frac{N_0}{2} \gamma_0^{p-1} \left( \frac{2m_ec \omega}{3eB_\perp}\right)^{-\frac{p-1}{2}}\frac{2^{\frac{p-3}{2}+1}}{\frac{p-3}{2}+2} \Gamma\left( \frac{p-3}{4}+ \frac{7}{3} \right) \Gamma\left( \frac{p-3}{4}+\frac{2}{3}\right) \notag \\ &= \frac{\sqrt{3} e^3 B_\perp N_0 \gamma_0^{p-1}}{8\pi^2 m_e c^2(p+1)} \left( \frac{m_ec \omega}{3eB_\perp}\right)^{-\frac{p-1}{2}} \Gamma \left( \frac{p}{4}+ \frac{19}{12} \right) \Gamma \left( \frac{p}{4} - \frac{1}{12}\right) \tag{10} \end{align}\]となります。
補遺: 数値積分スクリプト
以下に\(F(\chi_0)\)の計算に用いたPythonスクリプトを掲載いたします。ここではScipyの数値積分モジュールを用いています。詳しい使い方はScipyドキュメントの数値積分に関するページをご覧ください。
#!/usr/bin/env python3
from scipy.integrate import quad
import numpy as np
import matplotlib.pyplot as plt
# set integrand function
def integrand(t, chi0):
a = np.cosh(t)
b = np.cosh(5.0/3.0*t)
return np.exp(-chi0*a) * b / a
if __name__ == '__main__':
# set the range of chi0
chi0_min = 0.0
chi0_max = 3.0
num_chi0 = 1000
# set the list of chi0
chi0_list = np.linspace(chi0_min, chi0_max, num_chi0)
# set the lower limit of integration
a = 0
# set the upper limit of integration
b = 400
f = []
for chi0 in chi0_list:
ans = quad(integrand, a, b, args=(chi0, ))
f.append(chi0*ans[0])
plt.plot(chi0_list, f, color='g')
plt.xlim([0.0, 3.0])
plt.xlabel('χ0')
plt.ylabel('F')
plt.show()
参考文献
- [1] 平川浩正, 電気力学
- [2] Scipy Integration