Table of contents
パーカー不安定性 (Parker instability)
パーカー不安定性とは
降着円盤で重要な役割を果たす磁気不安定性にパーカー不安定性があります。重力によって層状になった大気中の磁束に働く浮力によって駆動される不安定性で、磁気浮力不安定性の一種です。
パーカー不安定性は、銀河円盤における星間ガス運の形成機構としてパーカーによって提唱されたものです(Parker 1966)。それ以外にも天体表面に磁束ループを持ち上げる働きがあることから、太陽表面における磁気的活動性の起源となる磁束浮上にも関連しています。
厳密な導出
式変形
ここではHoriuchi+ 1988のLinear Stability Analysisにしたがってパーカー不安定性の導出を行いましょう。
初期には、静止した流体と\(x\)方向の磁場があり、平行平板大気を作っているとします。以下では等温とプラズマベータ\(\beta = P/P_{\rm mag}\)一定を仮定します。重力は鉛直方向に働いていると考えて\({\bf F}_g = g(z) {\bf e}_z\)とします。
連続の式より
\[\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho {\bf v}) = 0\]運動量保存の式より
\[\frac{\partial }{\partial t} (\rho {\bf v}) + \nabla \cdot(\rho {\bf v}{\bf v})- \frac{1}{4\pi} ({\bf B} \cdot \nabla) {\bf B} + \nabla P_{\rm gas} + \frac{1}{8\pi} \nabla B^2 + \rho {\bf F}_g = {\bf 0}\]誘導方程式より
\[\frac{\partial {\bf B}}{\partial t} = \nabla \times ({\bf v} \times {\bf B})\]初期の物理量を\(\rho_0\)のように、添字の0をつけたもので表現します。すると、初期の物理量が満たす方程式は
\[\frac{\partial \rho_0}{\partial t} = 0\] \[{\bf v}_0 = {\bf 0}\] \[-\frac{1}{4\pi} ({\bf B}_0 \cdot \nabla) {\bf B}_0 + \nabla P_{0} + \frac{1}{8\pi} \nabla B_0^2 + \rho_0 g(z) {\bf e}_z = {\bf 0}\] \[\frac{\partial {\bf B}}{\partial t} = {\bf 0}\]初期の磁場の形は\({\bf B}_0 = B_x(z){\bf e}_x\)より
\[-\frac{1}{4\pi} B_x(z) \underbrace{\frac{\partial B_x}{\partial x}}_{=0} {\bf e}_x + \nabla P_0 + \frac{1}{8\pi} \nabla B_x^2 + \rho_0 g(z) {\bf e}_z = {\bf 0}\]この式と定温仮定\(C_s^2 = P_0/\rho_0 = {\rm uniform}, v_A^2 = B_x^2 / (4\pi \rho_0) = {\rm uniform}\)より
\[\begin{align} & C_s^2 \frac{\partial \rho_0}{\partial z} + \frac{1}{2}v_A^2 \frac{\partial \rho_0}{\partial z} + \rho_0 g(z) = (C_s^2 +\frac{1}{2}v_A^2) \frac{\partial \rho_0}{\partial z} + \rho_0 g(z) = 0 \ \Longrightarrow \ \frac{\partial \rho_0}{\partial z} = -\frac{g(z)}{C_s^2 + \frac{1}{2} v_A^2} \rho_0 \notag \\ & \Longrightarrow \ \ln (\rho_0 (z)/ \rho_0 (0)) = - \frac{\int_0^z g(z) dz}{C_s^2 + v_A^2/2} \ \Longrightarrow \ \rho_0 (z) = \rho_0(0) \exp \left\{ - \frac{\int_0^z g(z) dz}{C_s^2 + v_A^2/2} \right\} \notag \end{align}\]同様に\(P_0, B_x\)は
\[P_0 (z) = C_s^2 \rho_0 (z) = C_s^2 \rho_0 \exp \left\{ - \frac{\int_0^z g(z) dz}{C_s^2 + v_A^2/2} \right\} = P_0 (0) \exp \left\{ - \frac{\int_0^z g(z) dz}{C_s^2 + v_A^2/2} \right\}\] \[\begin{align} & B_x^2 = \beta \frac{P_0}{8\pi} = \frac{\beta}{8\pi} P_0 (0) \exp \left\{ - \frac{\int_0^z g(z) dz}{C_s^2 + v_A^2/2} \right\} \notag \\ &\Longrightarrow \ B_x = \left( \frac{\beta}{8\pi} P_0 (0) \right)^{1/2} \exp \left\{ - \frac{\int_0^z g(z) dz}{2 C_s^2 + v_A^2} \right\} = B_x (0) \exp \left\{ - \frac{\int_0^z g(z) dz}{2 C_s^2 + v_A^2} \right\} \notag \end{align}\]ここで、重力ポテンシャルを
\[\Phi = \int_0^z g(z) dz\]そして重力の形を、原点に中心星が作る重力場と見立てて
\[g(z) = GM \frac{z}{(r_0 + z^2)^{3/2}} = \frac{GM}{r_0^2} \frac{z/r_0}{(1+(z/r_0)^2)^{3/2}}\]とします。積分変数を\(Z = z/r_0\)に置換すると
\[\Phi = \frac{GM}{r_0^2} \int_0^{Z} \frac{Z}{(1+Z^2)^{3/2}} r_0 dZ = \frac{GM}{r_0} \int_0^z \tilde{g}(z) dz = \frac{GM}{r_0} \tilde{\Phi}\]
線形解析
ここで\(\tilde{}\)は規格化したものを表す記号です。すると\(\rho_0, P_0, B_x\)はそれぞれ
\[\rho_0 (z) = \rho_0 (0) \exp(-\epsilon \tilde{\Phi}), P_0 (z) = P_0 (0) \exp(-\epsilon \tilde{\Phi}), B_x (z) = B_x (0) \exp(-\frac{1}{2} \epsilon \tilde{\Phi})\]途中、\(\epsilon \equiv \frac{GM/r_0}{C_s^2+v_A^2/2}\)と定義しました。
ここに摂動が加わり、物理量が\(\rho_0 \rightarrow \rho_0 + \delta \rho, {\bf v}_0={\bf 0} \rightarrow \delta {\bf v}, P_0 \rightarrow P_0 + \delta P, {\bf B}_0 \rightarrow {\bf B}_0 + \delta {\bf B}\)に変化したとします。
連続の式より
\[\frac{\partial}{\partial t} (\rho + \delta \rho)+\nabla \cdot ((\rho + \delta \rho) + \delta {\bf v}) = \frac{\partial \delta \rho}{\partial t} + \nabla \cdot (\rho_0 \delta {\bf v}) = 0 \tag{1}\]運動量保存則より
\[\begin{align} & \frac{\partial}{\partial t} ((\rho + \delta \rho) \delta {\bf v}) + \nabla \cdot ((\rho + \delta \rho)\delta {\bf v} \delta {\bf v}) - \frac{1}{4\pi} (({\bf B}_0+\delta {\bf B})\cdot \nabla)({\bf B}_0 + \delta {\bf B}) \notag \\ & \quad + \nabla(P_0+ \delta P) + \frac{1}{8\pi} \nabla ({\bf B}_0+ \delta {\bf B})^2 - (\rho + \delta \rho) g {\bf e}_z = {\bf 0} \notag \\ & \Longrightarrow \ -\frac{1}{4\pi} (\delta {\bf B} \cdot \nabla) {\bf B}_0 -\frac{1}{4\pi} ({\bf B}_0 \cdot \nabla) \delta {\bf B} + \nabla \delta P + \frac{1}{4\pi} \nabla ({\bf B}_0 \cdot \delta {\bf B}) + \delta \rho g {\bf e}_z = {\bf 0} \tag{2} \end{align}\]誘導方程式より
\[\frac{\partial }{\partial t} ({\bf B}_0 + \delta {\bf B}) = \nabla \times (\delta {\bf v} \times ({\bf B}_0 + \delta {\bf B})) \ \Longrightarrow \ \frac{\partial}{\partial t} \delta {\bf B} = \nabla \times (\delta {\bf v} \times {\bf B}_0) \tag{3}\]摂動量を\(\delta P = \delta P(z) e^{i\omega t -ik_x x - ik_y y}\)のように変数分離して、一つのフーリエモードに着目してみましょう。
音速の式より
\[C_s^2 = \frac{P_0 +\delta P}{\rho_0 + \delta \rho} = \frac{P_0}{\rho_0}(1+\frac{\delta P}{P_0})(1-\frac{\delta \rho}{\rho_0}) = C_s^2 (1-\frac{\delta \rho}{\rho_0} + \frac{\delta P}{P_0}) \ \Longrightarrow \ \delta \rho = \frac{\delta P}{C_s^2}\]を用いて
\[\begin{align} (1) &\Longrightarrow \ \frac{\partial}{\partial t} \delta \rho + \frac{\partial}{\partial x} (\rho_0 \delta v_x) + \frac{\partial}{\partial y} (\rho_0 \delta v_y) + \frac{\partial}{\partial z} (\rho_0 \delta v_z) = 0 \ \Longrightarrow \ i\omega \frac{\delta P}{C_s^2} -ik_x \rho_0 \delta v_x - ik_y \rho_0 \delta - \frac{\partial }{\partial z} (\rho_0 \delta v_z) = 0 \notag \\ &\Longrightarrow \ i\omega \frac{\delta P}{C_s^2} -ik_x \rho_0 \delta v_x - ik_y \rho_0 \delta v_y + \frac{\partial }{\partial z} (\rho_0 \delta v_z) = 0 \tag{4} \end{align}\] \[(2のx成分) \ \Longrightarrow \ i\omega \rho_0 \delta v_x - \frac{1}{4\pi} \delta B_z \frac{\partial B_x}{\partial z} -ik_x \delta P = i\omega \rho_0 \delta v_x + \frac{g}{2C_s^2 + v_A^2} \frac{B_x}{4\pi} \delta B_z - ik_x \delta P = 0 \tag{5}\] \[(2のy成分) \ \Longrightarrow \ i\omega \rho_0 \delta v_y + ik_x \frac{B_x}{4\pi} \delta B_y - ik_y \delta P -ik_y \frac{B_x}{4\pi} \delta B_x = 0 \tag{6}\] \[(2のz成分) \ \Longrightarrow \ i\omega \rho_0 \delta v_z + ik_x \frac{B_x}{4\pi} \delta B_z + \frac{\partial}{\partial z} (\delta P + \frac{B_x}{4\pi} \delta B_x) + \delta \rho g = 0 \tag{7}\] \[\begin{align} (3のx成分) \ \Longrightarrow \ &i\omega \delta B_x - i k_y \delta v_y B_x+ B_x \frac{\partial \delta v_z}{\partial z} + \delta v_z \frac{\partial B_x}{\partial z} \notag \\ &= i\omega \delta B_x - ik_y \delta v_y B_x + B_x \frac{\partial \delta v_z}{\partial z} -\frac{g}{2C_s^2 + v_A^2} B_x \delta v_z = 0 \tag{8} \end{align}\] \[(3のy成分) \ \Longrightarrow \ i\omega \delta B_y + ik_x B_x \delta v_y = 0 \tag{9}\] \[(3のz成分) \ \Longrightarrow \ i\omega \delta B_z + ik_x B_x \delta v_z = 0 \tag{10}\] \[(9) \ \Longrightarrow \ \delta B_y = -\frac{k_x}{\omega} B_x \delta v_y\] \[(10) \ \Longrightarrow \ \delta B_z = -\frac{k_x}{\omega} B_x \delta v_z\]を代入して計算を行います。
\[(5) \ \Longrightarrow \ i\omega \rho_0 \delta v_x - \frac{gv_A^2}{2C_s^2 + v_A^2} \frac{k_x}{\omega} \rho_0 \delta v_z - ik_x \delta P = 0 \tag{11}\] \[(6) \ \Longrightarrow \ i \omega \rho_0 \delta v_y - i\frac{k_x^2}{\omega} v_A^2 \rho_0 \delta v_y - ik_y \delta P - ik_y \frac{B_x}{4\pi} \delta B_x = 0 \tag{12}\] \[(7) \ \Longrightarrow \ i\omega \rho_0 \delta v_z - i \frac{k_x^2}{\omega} v_A^2 \rho_0 \delta v_z + \frac{\partial}{\partial z} (\delta P + \frac{B_x}{4\pi} \delta B_x) + \frac{g}{C_s^2} \delta P = 0 \tag{13}\]さらに
\[(12) \ \Longrightarrow \ \delta v_y = k_y \frac{\delta P + \frac{B_x}{4\pi} \delta B_x}{\rho_0 (\omega - \frac{k_x^2}{\omega} v_A^2)}\]を代入して計算を行います。
\[(4) \ \Longrightarrow \ i\frac{\omega}{C_s^2} \delta P - ik_x \rho_0 \delta v_x - ik_y^2 \frac{\delta P + \frac{B_x}{4\pi} \delta B_x}{\omega-\frac{k_x^2}{\omega} v_A^2} + \frac{\partial }{\partial z} (\rho_0 \delta v_z) = 0 \tag{14}\] \[(8) \ \Longrightarrow \ i\omega \delta B_x -i\frac{k_y^2}{\rho_0} \frac{\delta P + \frac{B_x}{4\pi} \delta B_x}{\omega - \frac{k_x^2}{\omega} v_A^2} B_x + B_x \frac{\partial \delta v_z }{\partial z} - \frac{g}{2C_s^2 + v_A^2} B_x \delta v_z = 0 \tag{15}\]そして
\[(11) \ \Longrightarrow \ \delta v_x = \frac{ik_x \delta P + \frac{gv_A^2}{2C_s^2 + v_A^2} \frac{k_x}{\omega} \rho_0 \delta v_z}{i\omega \rho_0}\]を全てに代入します。
\[\begin{align} (14) &\Longrightarrow \ i(\frac{\omega}{C_s^2}-\frac{k_x^2}{\omega})\delta P - \frac{k_x^2}{\omega} \frac{g v_A^2}{2C_s^2 + v_A^2} \frac{\rho_0}{\omega}\delta v_z -i\omega k_y^2 \frac{\delta P + \frac{B_x}{4\pi} \delta B_x}{\omega^2 - k_x^2 v_A^2} + \frac{\partial}{\partial z} (\rho_0 \delta v_z) \notag \\ &= i\omega \frac{\omega^2 - k_x^2 C_s^2}{\omega^2 C_s^2} \delta P - \frac{k_x^2}{\omega^2} \frac{g v_A^2}{2C_s^2 + v_A^2} \rho_0 \delta v_z - i\omega \frac{k_y^2}{\omega^2 - k_x^2 v_A^2} (\delta P + \frac{B_x}{4\pi} \delta B_x) + \frac{\partial }{\partial z} (\rho_0 \delta v_z) = 0 \tag{16} \end{align}\] \[(15) \ \Longrightarrow \ i\omega \rho_0 \delta B_x - ik_y^2\omega \frac{\delta P + \frac{B_x}{4\pi}\delta B_x}{\omega^2 - k_x^2 v_A^2} B_x + B_x\frac{\partial}{\partial z} (\rho_0 \delta v_z) + B_x \delta v_z \frac{g}{2C_s^2 + v_A^2} \rho_0 = 0 \tag{17}\] \[\begin{align} &(16) + (17) \times \frac{\omega^2 - k_x^2 C_s^2}{\omega^2 C_s^2} \frac{B_x}{4\pi \rho_0} \ \Longrightarrow \notag \\ &i\omega \frac{\omega^2 - k_x^2 C_s^2}{\omega^2 C_s^2} (\delta P + \frac{B_x}{4\pi} \delta B_x) + \frac{g v_A^2}{2 C_s^2 + v_A^2}\left( \frac{\omega^2 - k_x^2 C_s^2}{\omega^2 C_s^2} - \frac{k_x^2}{\omega^2}\right) \rho_0 \delta v_z \notag \\ &- i\omega \frac{k_y^2}{\omega^2 - k_x^2 v_A^2} \left( 1+\frac{\omega^2 - k_x^2 C_s^2}{C_s^2 \omega^2} v_A^2 \right)(\delta P + \frac{B_x}{4\pi} \delta B_x) + \left( 1+ \frac{\omega^2 - k_x^2 C_s^2}{C_s^2 \omega^2 }v_A^2 \right) \frac{\partial }{\partial z} (\rho_0 \delta v_z) = 0 \notag \end{align}\]\(\frac{\partial }{\partial z} (\rho_0 \delta v_z)\)の係数の逆数をかけて式の整理を行います。途中、\(v_A^2 = 2 C_s^2 \alpha\)を用いてアルヴェーン速度を消去し、さらに\(k^2 \equiv k_x^2 + k_y^2\)とおくと
\[i\omega (\delta P + \frac{B_x}{4\pi} \delta B_x )の係数 \times \left( 1+\frac{\omega^2 - k_x^2 C_s^2}{C_s^2 \omega^2} v_A^2 \right)^{-1} = \frac{\omega^4 - (2\alpha + 1) k^2 C_s^2 \omega^2 + + 2\alpha C_s^4 k_x^2 k^2}{(\omega^2 - 2\alpha C_s^2 k_x^2) ((2\alpha+1)\omega^2 -2\alpha k_x^2 C_s^2)} C_s^{-2} \equiv - D_{\xi \eta}\] \[(\rho_0 \delta v_z)の係数 \times \left( 1+\frac{\omega^2 - k_x^2 C_s^2}{C_s^2 \omega^2} v_A^2 \right)^{-1} = \frac{\omega^2 - 2k_x^2 C_s^2}{(1+\alpha)((1+2\alpha)\omega^2 - 2\alpha C_s^2 k_x^2) C_s^2} \alpha g \equiv - D_{\xi \xi}\]一方で
\[\begin{align} &(16) \times \frac{B_x^2}{4\pi} - (17) \times \frac{B_x}{4\pi} \ \Longrightarrow \notag \\ &i\omega \frac{\omega^2 - k_x^2 C_s^2}{C_s^2 \omega^2}\frac{B_x^2}{4\pi} \delta P - \frac{k_x^2}{\omega^2} \frac{gv_A^2}{2C_s^2 + v_A^2} \frac{B_x^2}{4\pi} \rho_0 \delta v_z - i\omega \rho_0 \frac{B_x}{4\pi} \delta B_x - \frac{B_x^2}{4\pi} \frac{g}{2C_s^2 + v_A^2} \rho_0 \delta v_z = 0 \notag \\ & \underbrace{\Longrightarrow}_{/\rho_0} \ i\omega \frac{\omega^2 - k_x^2 C_s^2}{C_s^2 \omega^2} v_A^2 \delta P + i\omega \delta P -i\omega(\delta P + \frac{B_x}{4\pi} \delta B_x) - \frac{k_x^2}{\omega^2} \frac{g v_A^2}{2C_s^2 + v_A^2} v_A^2 \rho_0 \delta v_z - \frac{gv_A^2}{2C_s^2 + v_A^2} \rho_0 \delta v_z = 0 \notag \\ & \Longrightarrow \ i\omega \frac{g}{C_s^2} \delta P = i\omega \frac{\omega^2}{\omega^2 v_A^2 -k_x^2 C_s^2 v_A^2 + C_s^2 \omega^2} g (\delta P + \frac{B_x}{4\pi} \delta B_x)+ \frac{\omega^2 + k_x^2 v_A^2 }{\omega^2 v_A^2 -k_x^2 C_s^2 v_A^2 + C_s^2 \omega^2} \frac{g^2 v_A^2}{2C_s^2 + v_A^2} \rho_0 \delta v_z \notag \end{align}\]これと\((13)\times i\omega\)より
\[\begin{align} & -\omega^2 \rho_0 \delta v_z + k_x^2 v_A^2 \rho_0 \delta v_z + i\omega \frac{\partial }{\partial z} (\delta P + \frac{B_x}{4\pi} \delta B_x) + i\omega \frac{g}{C_s^2} \delta P = 0 \notag\\ & \Longrightarrow \ -(\omega^2 - k_x^2 v_A^2) \rho_0 \delta v_z + i\omega \frac{\partial}{\partial z} (\delta P + \frac{B_x}{4\pi} \delta B_x) \notag \\ & + i\omega \frac{\omega^2}{\omega^2 v_A^2 - k_x^2 C_s^2 v_A^2 + C_s^2 \omega^2} g (\delta P + \frac{B_x}{4\pi} \delta B_x) + \frac{\omega^2 + k_x^2 v_A^2}{\omega^2 v_A^2 - k_x^2 C_s^2 v_A^2 + C_s^2 \omega^2} \frac{g^2 v_A^2}{2C_s^2 + v_A^2} \rho_0 \delta v_z = 0 \notag \end{align}\]この式の係数のみに着目しましょう
\[i\omega (\delta P + \frac{B_x}{4\pi} \delta B_x)の係数 = \frac{\omega^2}{(2\alpha + 1) \omega^2 - 2\alpha C_s^2 k_x^2} \frac{g}{C_s^2} \equiv - D_{\eta \eta}\] \[(\rho_0 \delta v_z)の係数 = - (\omega^2 - 2\alpha k_x^2 C_s^2) \left( 1- \frac{\omega^2 + 2\alpha k_x^2 C_s^2}{\omega^2 - 2\alpha k_x^2 C_s^2} \frac{g^2\alpha}{(1+\alpha)C_s^2} \frac{1}{(2\alpha + 1) \omega^2 - 2\alpha k_x^2 C_s^2} \right) \equiv - D_{\eta \xi}\]よって最終的に方程式は、\(\xi \equiv \rho_0 \delta v_z, \eta \equiv i\omega(\delta P + \frac{B_x}{4\pi}) \delta B_x\)
\[\frac{\partial \xi}{\partial z} -D_{\xi \eta} \eta - D_{\xi \xi} \xi = 0\] \[\frac{\partial \eta}{\partial z} - D_{\eta \eta} \eta - D_{\eta \xi} \xi = 0\]この式をまとめて
\[\frac{\partial }{\partial z} \left( \begin{array}{c} \xi \\ \eta \end{array} \right) = \left( \begin{array}{cc} D_{\xi \xi} & D_{\xi \eta} \\ D_{\eta \xi} & D_{\eta \eta} \end{array} \right) \left( \begin{array}{c} \xi \\ \eta \end{array} \right)\]のように書けます。これを数値積分してやれば良いことがわかります。
境界条件
\(z \rightarrow \infty\)で2つの物理量は減衰するような境界条件を設定します。すなわち
\[\xi = \xi_0 e^{\kappa z}\]のような形を仮定して\(\kappa\)の値を求めましょう。さらに\(z\)が大きいところではほとんど重力\(g\)はほぼ値が変わらないと考えて(WKB近似)
\[\frac{\partial \xi}{\partial z} = \kappa \xi = D_{\xi \xi} \xi + D_{\xi \eta} \eta\]とします。すると
\[\begin{align} &\frac{\partial^2 \xi }{\partial z^2} = \kappa^2 \xi = D_{\xi \xi} \frac{\partial \xi}{\partial z} + D_{\xi \eta} \frac{\partial \eta}{\partial z} = D_{\xi \xi} \kappa \xi + D_{\xi \eta} (D_{\eta \xi} \xi+ D_{\eta \eta} \eta) = D_{\xi \xi} \kappa \xi + D_{\xi \eta} D_{\eta \xi} \xi + D_{\eta \eta} (\kappa \xi - D_{\xi \xi} \xi) \notag \\ &\Longrightarrow \ \kappa^2 -( D_{\xi \xi} + D_{\eta \eta}) \kappa + D_{\xi \xi}D_{\eta \eta} - D_{\xi \eta} D_{\eta \xi} = 0 \notag \end{align}\] \[\therefore \ \kappa = \frac{D_{\xi \xi}+ D_{\eta \eta} \pm \sqrt{(D_{\xi \xi}+D_{\eta \eta})^2 -4 (D_{\xi \xi}D_{\eta \eta} -D_{\xi \eta} D_{\eta \xi})}}{2}\]\(\kappa < 0\)のとなるような解を選択するので、\(\kappa_{-} = \frac{D_{\xi \xi}+ D_{\eta \eta} - \sqrt{(D_{\xi \xi}+D_{\eta \eta})^2 -4 (D_{\xi \xi}D_{\eta \eta} -D_{\xi \eta} D_{\eta \xi})}}{2}\)とします。
また\(z=0\)での境界条件として、\(\xi, \eta\)のどちらかが反対称を仮定します。すなわち、\(z=0\)でどちらかの値が0であることを境界条件とします。
数値積分の方法
ルンゲ・クッタ法を用います。\(z=\infty\)を出発点として、\(z=0\)まで積分を実行します。
論文の結果
ルンゲ・クッタによる積分計算などをすっ飛ばして、ここでは論文の結果の中でも重要な部分をかいつまんでご紹介いたします。
不安定性が成長するモードの波数依存性は?
- 波数が大きい(波長が小さい): 磁気張力が大きくなり成長しない
- 波数が小さい(波長が大きい): 流体要素が滑り降りる時間が長くなり浮力が大きくなりにくい
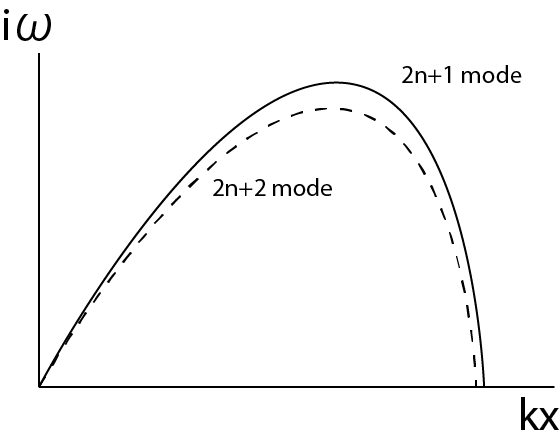
上図の2n+1モードはfundamental, 2nd-harmonics, 4th…に対応し、2n+2モードは1st-harmonics, 3rd…に対応します。2n+1と2n+2のモードの成長率がペアとなって現れます。
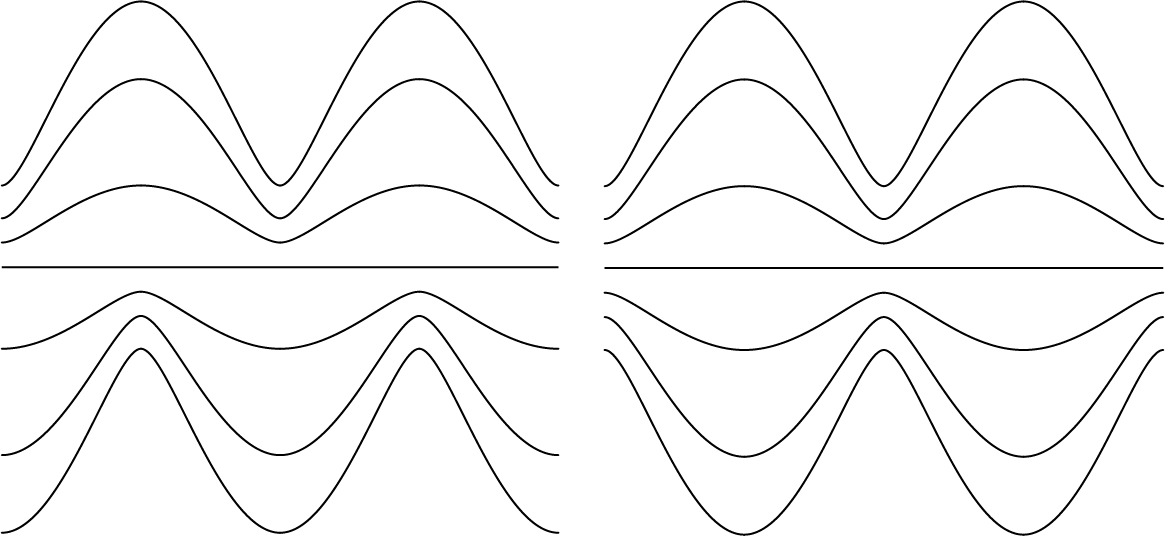
どういう形のモードが成長しやすい?
同じ波数でも、赤道面を挟んですべり対称のモード(下図左パネル)の方が鏡像対称(下図右パネル)よりも成長率が大きくなります。
直感的な導出
以下ではさらに直感的に導出するために、\(z\)方向の重力も一様とします。等温とプラズマベータ一定を仮定し、密度と磁場は\(\rho=\rho(z), {\bf B} = B_x(z) {\bf e}_z\)のように書かれるものとします。重力と磁気圧・ガス圧勾配力の釣り合いの式より
\[\frac{d}{dz} \left( P+\frac{B^2}{8\pi} \right) = - \rho g \ \Longrightarrow \ (1+\beta^{-1})C_s^2 \frac{d\rho}{dz} = -\rho g\] \[\therefore \ \frac{d\ln \rho}{dz} = -\frac{g}{C_s^2 (1+\beta^{-1}) } \ \Longrightarrow \ \rho(z) = \rho_0 e^{-z/H'}\]ここで\(H'\equiv C_s^2 (1+\beta^{-1})/g\)は磁場がある場合の等温平行平板のスケールハイトです。磁気圧力勾配に大気が支えられることによって、スケールハイトが大きくなっていることがわかります。ちなみに\(\beta \rightarrow \infty\)では、磁場がない場合の静水圧平衡の式
\[\rho(z) = \rho_0 e^{-z/H} \ (H \equiv C_s^2/g)\]に一致します。
さて、この静水圧平衡状態にある系において雪道が加わり、図のように磁力線の一部が\(\Delta z \ll 1\)だけ持ち上がったとしましょう。このとき、磁力線と共に持ち上がった磁力線内部の流体の密度を\(\rho_{\rm in}(\Delta z)\)、磁力線の外側の流体の密度を\(\rho_{\rm out} (\Delta z)\)とします。\(z=0\)を持ち上げ前の高さにとします。
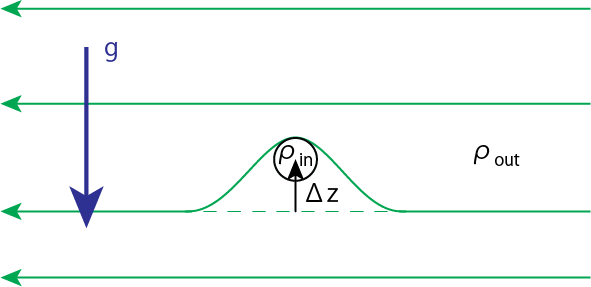
磁力線とともに持ち上がった内部と外部に密度差があれば、内部は浮力を受けます。これを計算していきましょう。ここで、流体の上昇が起きた時間ずけーるは、音波が雪道のスケールを伝播する時間スケールに比べて十分ゆっくりとします。すなわち、摂動は常に周囲と圧力平衡であると考えます。内部の流体は上昇後の磁力線に沿った方向にのみ運動できるので、内部の流体の磁気圧は上昇前後で変化しないと考えてよいでしょう。したがって内部と外部の密度差は
\[\Delta \rho = \rho_{\rm in}(\Delta z) - \rho_{\rm out}(\Delta z) = \rho_0(e^{-\Delta z/H}- e^{-\Delta z/H'}) \simeq \rho_0 \left( 1-\frac{\Delta z}{H} -1 + \frac{\Delta z}{H'}\right) = \rho_0 \Delta z(H'^{-1}-H^{-1}) < 0\]で与えられます。この値は必ず負の値となるため、内部は周囲より軽くなることがわかります。内部の流体は、この密度差の分の浮力を受けるので
\[F_{\rm buoyancy} = - \Delta \rho g \simeq \rho_0 g \Delta z(H^{-1} -H'^{-1})\]となります。一方で上図のように磁力線が変形すると、下向きに磁気張力が働きます。磁気聴力の大きさは、磁力線の曲率半径を\(R\)とすると大雑把に見積もって
\[F_{\rm tension} \simeq \frac{1}{4\pi} \frac{B_0^2}{R}\]です。ここで0の添字は、磁力線がそのまま上昇したことにより上昇前の位置での磁場の強さが保たれている、ということからくるものです。
では次の図のようにして曲率半径\(R\)と\(\Delta z\)の関係式を導きましょう。半径\(R\)の縁に内接する直角三角形を考え、相似関係を利用します。すると
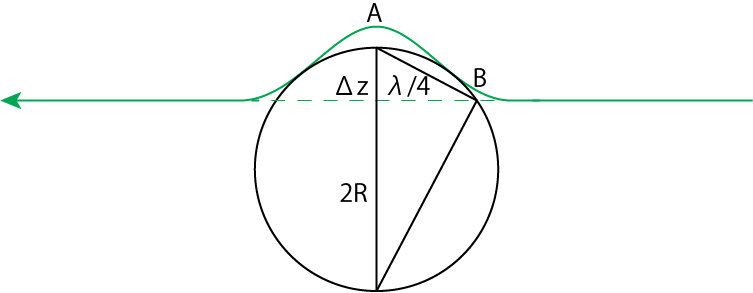
ここで\(\lambda\)は摂動のおおよその波長であり、辺ABを\(\lambda/4\)とした大雑把な見積もりです。
\(F_{\rm buoyancy} > F_{\rm tension}\)のとき内部の流体は上昇を続けることになり、これは不安定であることを意味します。
よってスケールハイトの10倍程度の長さの摂動が加わったとき、浮力が張力を上回り、流体と磁力線は上昇を続けることになります。
このときの成長率も大雑把に見積もりましょう。(速度\(v_A\)でスケールハイト\(H\)を上昇するのにかかる時間スケール)=(パーカー不安定性が成長するのにかかる時間スケール)と考えると
\[\tau_A = \frac{v_A}{H} \ \Longrightarrow \ \nu_{\rm Parker} \simeq H/v_A\]となります。
直感的理解
以上は式変形からの導出でしたが、ポイントとなったのは摂動内部の流体が磁力線に沿った方向にのみ広がるという点です。これをもう少し別の視点から考察してみましょう。磁力線の一部が持ち上がることにより、磁力線と共に持ち上がった流体要素は磁力線に沿って(滑り台を下りるように)落ちていきます。すると持ち上がった頂上部分は周囲よりも密度が薄くなり、浮力を感じるようになります。この浮力が磁気張力よりも強ければさらに上昇が続く、という一連の流れがこの不安定性の本質です。
天体物理現象の例: 太陽表面のコロナループ
対流層で強められた磁場が浮上しコロナにまで達する大きなループを形成します。光球面での付け根に黒点を形成すると考えられています。
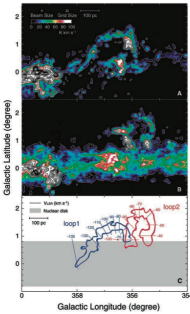
天体物理現象の例: 銀河中心方向に見つかった分子雲ループ
銀河中心方向の電波によるCO輝線観測により分子雲のループが見つかっています(Fukui+, 2006)。これは銀河円盤のパーカー不安定性によりできた構造であると指摘されています。
参考文献
[1] Fukui et al., 2006, “Modecular Loops in the Galactic Center: Evidence for Magnetic Flotation”
[2] Horiuchi et al., 1988, “Parker Instability in Nonuniform Gravitational Fileds. I. Linear Stability Analysis”
[3] Parker, 1966, “The Dynamical State of the Interstellar Gas and Field”
[4] Priest, “Magnetohydrodynamics of the Sun”
[5] 柴田一成, 横山央明, 工藤哲洋, “宇宙電磁流体力学の基礎”
[6] 柴田一成, 福江純, 松元亮治, 嶺重慎, “活動する宇宙”
[7] 観山正見, 二間瀬敏史, 野本憲一, “天体物理学の基礎 II”