Table of contents
電子の縮退とチャンドラセカール限界質量
白色矮星や中性子星などは、その星を構成する粒子の縮退圧によって支えられていると考えられています。そして縮退圧により支えることができる恒星の質量には上限があることが知られています。 特に白色矮星については、この限界質量のことをチャンドラセカール質量限界(Chandrasekhar’s mass limit)と呼びます。以下では縮退した電子ガスの状態方程式を考え、白色矮星の場合にこれを求めてみましょう。
フェルミ粒子の縮退条件
フェルミ粒子からなる物質系の密度が十分大きな状態では縮退(degeneracy)という現象が起こります。ここでは簡単のため、電子・陽子、または中性子等からなる単原子分子気体を考えましょう。 粒子数密度\(N\)が十分小さい時、ガスの熱運動はマクスウェル・ボルツマン分布で表現され、理想気体として振る舞います。このとき、運動量\(p\)を持つ粒子の単位位相空間体積あたりの粒子数\(f(p)\)は、以下のように与えられます。
\[f(p) = f_\mathrm{MB} (p) \equiv \frac{N}{(2\pi mk_B T)^{3/2}} e^{-\frac{p^2}{2m k_B T}} \tag{1}\]で与えられます。
量子力学から、位置と運動量からなる位相空間(実空間x運動量空間の6次元空間)の単位体積あたりの、スピン1/2の粒子の状態数は、スピンの自由度が2であることから\(2 / h^3\)で与えられます。 一方、フェルミ粒子に対するパウリの排他原理により、同じ状態を持つ2つ以上の粒子が存在することは禁止されています。この原理は、分布関数\(f(p)\)に対して
という条件を課すことを意味します。したがって、マクスウェル・ボルツマン分布がパウリの排他原理と矛盾しないためには
\[\frac{2}{h^3} > f_M(p) = \frac{N}{(2\pi mk_B T)^{3/2}} e^{-\frac{p^2}{2m k_B T}} \tag{3}\]でなければなりません。この条件が全ての取りうる運動量\(0 < p < \infty\)で成り立つためには、一番値の大きい\(p=0\)で成り立っていれば良いでしょう。すなわち、ガスが理想気体として振る舞うための条件は
\[\frac{2}{h^3} \geq \frac{N}{(2\pi mk_B T)^{3/2}} e^{-\frac{p^2}{2m k_B T}} \quad \left( \equiv \frac{2}{h^3} e^{\eta_e} \quad 電子の場合\right) \tag{4}\]と表現されます。(4)式から、この条件は実空間での粒子数密度\(N\)が大きく、温度が低いような状況で満たされなく可能性があります。このときガスは理想気体の性質からずれ、縮退の影響が現れます。 このような状況では、運動量\(p\)が小さいところで(2)式により粒子数密度が抑えられ、その分、運動量の大きな粒子の密度がマクスウェル・ボルツマン分布に比べて大きくなります(下図)。
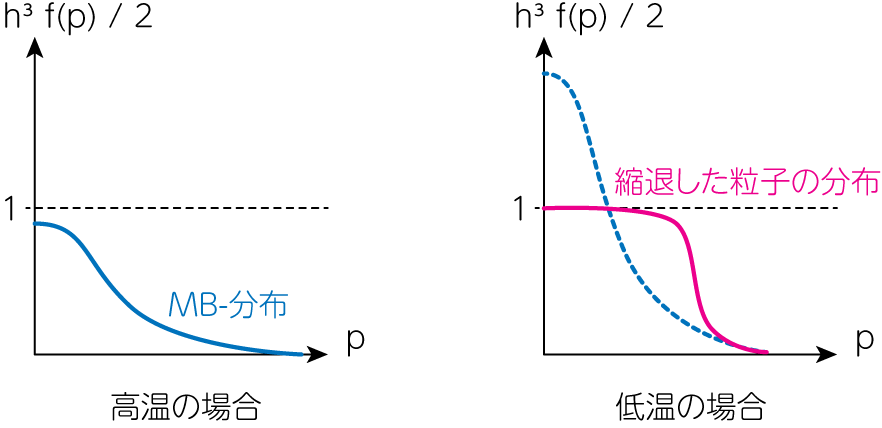
(4)式の不等式では、粒子の質量が小さい場合ほど満たさなくなりやすいことがわかります。そのため、恒星の構造の進化では電子の縮退が重要な働きをします。電子に対して(4)式が満たされなくなる場合とは、\(\eta_e > 0\)に対応します。 また、\(N_e = \rho/ (\mu_e m_p)\)の関係を用いると(\(\mu_e\)は電子の平均分子量、詳細は後述)、電子の縮退が始まる条件は、cgs単位系で
\[\frac{\rho}{\mu_e T^{3/2}} > \frac{2m_p (2\pi m_e k_B)^{3/2}}{h^3} \sim 8.05 \times 10^{-9} \tag{5}\]と求まります。例えば、電離したヘリウム核と電子だけからなるガス\(\mu_e =2\)で、温度が\(10^8\)Kの場合には、\(\rho > 1.6 \times 10^4 \ \mathrm{g/cm^3}\)で電子の縮退が起こります。
完全縮退電子気体の状態方程式
一般の粒子に対して、位置と運動量が作る位相空間における運動量\(p\)の粒子数密度は
\[f_e (p) = \frac{1}{h^3} \sum_j \frac{g_j}{\exp [-\eta + (\mathcal{E}_j + \mathcal{E}_p) / (k_B T)] \pm 1} \tag{6}\]で表現されます。\(\mathcal{E}_j\)は粒子の内部状態\(j\)のエネルギー、\(g_j\)はその状態の統計的重率です。そして\(\mathcal{E}_p\)は粒子の運動エネルギーを表し、\(\eta\)は化学ポテンシャルを\(k_B T\)で割った量です。 最後の複合の\(+\)はフェルミ粒子、\(-\)符号はボーズ粒子に対して適用されます。これを自由電子に対して考えると、電子に対する分布関数は
\[f_e (p) = \frac{2/h^3}{\exp [-\eta + \mathcal{E}_p/(k_B T)] + 1} \tag{7}\]となります。自由電子を考えるため\(\mathcal{E}_0 = 0\)、そして電子のスピン方向の自由度より\(g_0 = 2\)としました。電子の運動エネルギーは
\[\mathcal{E}_p = \sqrt{p^2 c^2 + m_e^2 c^4} - m_e c^2 \tag{8}\]で与えられます。全運動量で\(f_e(p)\)で積分することで、実空間での単位体積あたりの粒子数(数密度)を得ます。
\[n_e = \frac{\rho}{\mu_e m_p} = \int_0^\infty 4\pi p^2 f_e(p) dp = \frac{8\pi}{h^3} \int_0^\infty \frac{p^2}{\exp [-\eta + \mathcal{p}/(k_B T)] + 1} dp \tag{9}\]また、電子の分圧\(P_e\)を計算しましょう。圧力はある方向(ここでは\(z\)方向とします)への運動量フラックスとして定義されるので
\[P_e = \iiint d^3 \mathbf{p} f_e(\mathbf{p}) \underbrace{v_z p_z}_{v p \cos^2 \theta} = \int_0^\infty dp p^2 f_e(p) v p \int_{4\pi} \cos^2 \theta d\Omega = \frac{4\pi}{3} \int_0^\infty dp f_e(p) v p^3\]ここで速度\(v\)はハミルトンの関係式\(\dot{q} = \frac{\partial H}{\partial p}, \dot{p} = - \frac{\partial H}{\partial q}\)より
\[v = \frac{\partial \mathcal{E}_p}{\partial p} = \frac{c^2 p }{\sqrt{p^2 c^2 + m^2 c^4}} = \frac{pc}{\sqrt{p^2 + m_e^2 c^2}}\]と求まるので、以上から
\[P_e = \frac{8\pi c}{3h^3} \int_0^\infty \frac{p^4 (p^2 + m_e^2 c^2)^{-1/2}}{\exp [-\eta + \mathcal{E}_p /(k_B T)] + 1} dp \tag{10}\]のように書かれます。同様に電子の内部エネルギー密度\(E_e\)を求めましょう。
\[E_e = \int_0^\infty \mathcal{E}_p f(p) 4\pi p^2 dp = \frac{8\pi}{h^3} \int_0^\infty \frac{\mathcal{E}_p p^2 }{\exp [-\eta + \mathcal{E}_p / (k_BT)] + 1} dp \tag{11}\]これらの式から、例えば\(\rho, T\)が与えられると(9)式から\(\eta (= 化学ポテンシャル//(k_B T))\)が求められ、これを(10), (11)式に代入すれば\(P_e, E_e\)が求まります。 実際に恒星の内部構造を計算する際には(9), (10), (11)式を解いて得られた\(\rho, T, P_e, E_e\)間の関係を表にしたものを用意し、内挿によって知りたい\(\rho, T\)に対する\(P_e, E_e\)を算出することが行われます。
電子が完全に縮退した状態とは、(4)式において\(\eta_e \gg 1\)の場合と表現されます。このとき
\[\frac{h^3}{2} f_e (p) = \left\{ \begin{array}{ll} 1 & (\mathcal{E}_p / (k_B T) \leq \eta)\\ 0 & (\mathcal{E}_p / (k_B T) > \eta) \end{array}\right. \tag{12}\]のように表されます。上の状態は、粒子の運動量分布が温度に全く依存していないことがわかります。依存関係がないことから、これを縮退(degenerate)した状態と呼びます。 フェルミエネルギーを\(\mathcal{E}_F \equiv \eta k_B T\)と定義し、\(\mathcal{E}_p = \mathcal{E}_F\)のときの運動量(これをフェルミ運動量と呼びます)を\(p_F\)と書きます。(9)式は、完全に縮退した状態に対して
\[n_e = \frac{\rho}{\mu_e m_p} = \frac{8\pi}{h^3} \int_0^{p_F} p^2 dp = \frac{8\pi p_F^3}{3h^3} \tag{13}\]のように書けます。ここで、無次元化したフェルミ運動量を
\[x_F \equiv \frac{p_F}{m_e c} \tag{14}\]のように定義すると(13)式より
\[\frac{\rho}{\mu_e} = \frac{8\pi m_p}{3} \left( \frac{m_e c}{h}\right)^3 x_F^3 = Cx_F^3 \tag{15}\]のように変形されます。電子の場合は\(C \sim 9.7 \times 10^5 \ \mathrm{g/cm^3}\)、中性子に対しては\(C \sim 6.1 \times 10^{15} \ \mathrm{g/cm^3}\)などです。 \(x_F \sim 1\)で相対論的な効果が重要となるため、上式は完全に縮退した状態では密度が\(\rho/\mu_e \sim 10^6 \mathrm{g/cm^3}\)よりも高くなると相対論的効果が大きくなることを示しています。 完全縮退した電子の分圧は(10)式より
\[P_e = \frac{8\pi c}{3h^3} \int_0^{p_F} \frac{p^4 }{\sqrt{p^2 + m_e^2 c^2}} dp = \frac{8 \pi c^5 m_e^4}{3h^3} \int_0^{x_F} \frac{x^4}{\sqrt{1+x^2}}dx = B f(x_F) \tag{16}\]ここで
\[f(x_F) = 8 \int_0^{x_F} \frac{x^4}{\sqrt{1+x^2}}dx \tag{17}\]を求めましょう。\(x = \sinh y\)とおくと、\(dx = \cosh y\)、さらに積分区間は\([0, x_F]\)のとき\([0, \sinh^{-1} x_F]\)となります。よって
\[f(x_F) = 8 \int_0^{\sinh^{-1} x_F} \frac{\sinh^4 y}{\sqrt{1+\sinh^2y}} \cosh y dy\]ここで双曲線関数の性質
\[\cosh^2 y - \sinh^2 y = 1 \ \Longrightarrow \ \cosh y = \sqrt{1+\sinh^2 y} \quad (\cosh y > 0)\] \[\cosh 2y = \frac{e^{2y} + e^{-2y}}{2} = \frac{(e^y + e^{-y})^2 + (e^y - e^{-y})}{4} = \cosh^2 y + \sinh^2 y = 1 + 2 \sinh^2 y = 2 \cosh^2 y -1\] \[\sinh 2y = \frac{e^{2y} - e^{-2y}}{2} = \frac{(e^y + e^{-y}) (e^y - e^{-y})}{2} = 2 \sinh y \cosh y\]などを用いると
\[\begin{align} f(x_F) &= 8 \int_0^{\sinh^{-1} x_F} \sinh^4 y dy = 8 \int_0^{\sinh^{-1} x_F} \frac{1}{4} (\cosh 2y -1)^2 dy = 2 \int_0^{\sinh^{-1} x_F} (\cosh^2 2y -2 \cosh 2y +1) dy \notag \\ &= 2 \int_0^{\sinh^{-1} x_F} \left( \frac{\cosh 4y + 1}{2} -2 \cosh 2y +1 \right) dy = \left[ \frac{1}{4} \sinh 4y - 2 \sinh 2y + 3 y\right]_0^{\sinh^{-1} x_F} \notag \\ &= \left[ \frac{1}{2} \sinh 2y \cosh 2y - 4 \sinh y \cosh y + 3 y\right]_0^{\sinh^{-1} x_F} = \left[ \sinh y \cosh y (1+2 \sinh^2 y) - 4 \sinh y \cosh y + 3 y\right]_0^{\sinh^{-1} x_F} \notag \\ &= \left[ \sinh y \sqrt{1+\sinh^2 y} (2 \sinh^2 y - 3) + 3 y\right]_0^{\sinh^{-1} x_F} = x_F \sqrt{1+x_F^2} (2x_F^2 -3) + 3 \sinh^{-1} x_F \tag{18} \end{align}\]と求まります。(13), (14)式より\(x_F\)はガス密度\(\rho\)にしか依存しない量です。このことと、(16), (18)式から、完全に縮退した状態では電子の分圧\(P_e\)は密度だけで決まり、温度は無関係であることがわかります。 そのため、縮退した状態で核融合による熱の発生が起こると、温度による圧力の変化がなく膨張による冷却も働きません。よって熱的暴走(フラッシュ)が起こります。
平均分子量
一般に完全電離した電子気体では、その圧力は核子(イオン)気体と電子気体の分圧の和により計算されます。先程の議論から、電子気体は縮退していますが、核子気体は縮退していない状況を考えましょう。 このときの圧力は、電子気体の縮退圧が圧倒的に大きいとして
\[P_\mathrm{tot} = P_\mathrm{ion} + P_\mathrm{e} \simeq P_\mathrm{e} \tag{19}\]が良い近似で成り立っているとします。以降、化学組成が一様であるような単純な白色矮星の場合を考えましょう。水素の質量比を\(X\)、ヘリウムの質量比を\(Y\)、その他の元素の質量比を\(X_n \ (n > 4)\)のように表すことにします。白色矮星は完全電離ガスにより形成されていると考えて、単位体積中の電子数は
\[n_e \simeq \frac{\rho X}{m_p} + \frac{2 \rho Y}{4m_p} + \sum_{n > 4}^{n_\mathrm{max}} \frac{n}{2} \frac{\rho X_n}{n m_p} = \frac{\rho}{m_p} \left( X + \frac{Y}{2} + \frac{Z}{2}\right) = \frac{\rho}{2 m_p} (1+X) \equiv \frac{\rho}{\mu_e m_p} \tag{20}\]のように与えられます。ここで
\[Z = \sum_{n>4}^{n_\mathrm{max}} X_n , \quad X + Y + Z = 1, \quad \mu_e \equiv \frac{2}{1+X} \tag{21}\]などを用いました。\(Z\)はその定義からヘリウムより重たい原子の質量比、そして\(\mu_e\)は自由電子1個あたりの平均分子量です。(20)式の\(\rho X\)は単位体積あたりの水素の質量で、それを\(m_p\)で割ったものは単位体積あたりの水素原子の数になります。今は完全電離を考えているため、水素の原子数がそのまま電子数としてカウントされます。次の\(\rho Y\)は単位体積あたりのヘリウムの質量で、それを\(4 m_p \simeq 2 m_p + 2 m_n\)で割ったものがヘリウム原子の数になります。中性ヘリウムは電子を2つ持っているため、完全電離の場合には1つのヘリウムから2つの電子が放出されます。2の因子がかかっているのはそのためです。
(21)式で定義された電子の平均分子量\(\mu_e\)は、電子1つあたりの分子量を表す量です。もしこの系に水素しか存在しないならば、\(X=1\)を代入して\(\mu_e = 1\)となります。これは元々、中性水素が1つの電子を持つことに対応します。1つの電子の存在は1つの水素原子が同じ系内にいることを意味しているため、電子1つあたりの分子量も水素1個分というように数えることができます。仮に水素が存在せず、ヘリウムのみが場合、\(X=0\)を代入することで\(\mu_e = 2\)を得ます。これは質量数4の中性ヘリウムが2つの電子を持つことから、電子1つあたりの分子量は質量数2に相当するということを表しています。
(13), (14), (20)式より
途中の\(\lambda_c\)は電子コンプトン波長です。この式と(16)式を合わせると\(P_e = B f(A \rho^{1/3})\)と書けます。これはポリトロープの時とは異なり、\(\rho\)の係数である\(K\)が介入していないため、質量と半径とを独立に任意に与えることができません。すなわち、状態方程式はポリトロープ的ですが、パラメータ\(K\)は状態方程式により与えることができるため、星の構造を決定するには半径か質量のどちらか1つを与えてやればよいことがわかります。
静水圧平衡の式からの変形
簡単のため、この縮退圧で支えられている恒星は球対称であるとします。重力と圧力勾配の釣り合いで形成されている静水圧平衡の式より
\[\frac{1}{r^2} \frac{d}{dr} \left( \frac{r^2}{\rho} \frac{dP}{dr}\right) = -4\pi G\rho \tag{23}\]これの式変形を行うことで、数値的に物理量が求められる式を導出しましょう。(16)式より
\[\frac{dP}{dr} = B \frac{df}{dr} = B \overbrace{\frac{dx_F}{dr}}^{(22)} \underbrace{\frac{df}{dx_F}}_{(17)} = \frac{1}{3} A B \rho^{-2/3} \frac{d\rho}{dr} \frac{8 A^4 \rho^{4/3}}{\sqrt{1+A^2 \rho^{2/3}}} \tag{24}\]を得ます。計算を進めるために、以下の量を導入しましょう。
\[z^2 \equiv x_F^2 + 1, \quad \varphi \equiv \frac{z}{z_c}, \quad \zeta \equiv \frac{r}{\alpha}, \quad \alpha \equiv \sqrt{\frac{2B}{\pi G}} \frac{A^3}{z_c} \tag{25}\]ここで添字の\(c\)は星の中心での物理量を表す定数です。
\[\varphi^2 z_c^2 \underbrace{=}_{(22)} A^2 \rho^{2/3} + 1 \tag{26}\]より、この両辺を\(r\)で微分すると
\[2 z_c^2 \varphi \frac{d\varphi}{dr} = \frac{2}{3} A^2 \rho^{-1/3} \frac{d\rho}{dr} \tag{27}\](25), (26), (27)式を用いて(24)式を整理します。
\[\frac{dP}{dr} = \frac{1}{3} A B \rho^{-2/3} 3 z_c^2 \varphi \frac{1}{\alpha} \frac{d\varphi}{d\zeta} \frac{\rho^{1/3}}{A^2} \frac{8 A^4 \rho^{4/3}}{\varphi z_c} = 8 A^3 B z_c \frac{\rho}{\alpha} \frac{d\varphi}{d\zeta} \ \underbrace{\Longrightarrow}_{\times r^2 / \rho} \ \frac{r^2}{\rho} \frac{dP}{dr} = 8A^3 B z_c \alpha \zeta^2 \frac{d\varphi}{d\zeta}\]さらにこれの両辺を\(r\)で微分したものを整理します。
\[\frac{d}{dr} \left( \frac{r^2}{\rho} \frac{dP}{dr} \right) = 8 A^3 B z_c \frac{d}{d\zeta} \left( \zeta^2 \frac{d\varphi}{d\zeta}\right) \ \underbrace{\Longrightarrow}_{\times 1/r^2} \ \frac{1}{r^2}\frac{d}{dr} \left( \frac{r^2}{\rho} \frac{dP}{dr} \right) = \frac{8A^3 B z_c}{\alpha^2} \frac{1}{\zeta^2} \frac{d}{d\zeta} \left( \zeta^2 \frac{d\varphi}{d\zeta} \right) = \frac{4\pi Gz_c^3}{A^3} \frac{1}{\zeta^2} \frac{d}{d\zeta} \left( \zeta^2 \frac{d\varphi}{d\zeta}\right)\](22)式より
\[\frac{4\pi G z_c^3}{A^3} \frac{1}{\zeta^2} \frac{d}{d\zeta} \left( \zeta^2 \frac{d\varphi}{d\zeta} \right) = -4\pi G \rho \underbrace{=}_{(26)} - 4\pi G \left( \frac{\varphi^2 z_c^2 - 1}{A^2}\right)^{3/2} \ \Longrightarrow \ \frac{1}{\zeta^2} \frac{d}{d\zeta} \left( \zeta^2 \frac{d\varphi}{d\zeta} \right) = - \left( \varphi^2 - \frac{1}{z_c^2}\right)^{3/2} \tag{28}\]質量と半径
恒星の全質量\(M\)と半径\(R\)を求めましょう。ここので恒星の半径とは、「(28)式を中心から数値積分していった時に、最初に密度がゼロになるところ」と定めます。 言い換えると\(\zeta = \zeta_1\)において(21)式から\(x_{F, 1} = 0\)、(25)式から\(z_1 = 1, \varphi_1 = 1/z_c\)となるような場所のことを指します。ここで添字の1は恒星表面での値を表します。
(28)式の途中式より
となります。半径については
\[R = \alpha \zeta_1 = \sqrt{\frac{2B}{\pi G}} \frac{A^3}{z_c} \zeta_1 = \sqrt{\frac{2}{\pi G}} \left( \frac{\pi m_e^4 c^5}{3h^3}\right)^{1/2} \frac{h^3}{m_e^3 c^3} \frac{3}{8\pi \mu_e m_p} \frac{\zeta_1}{z_c} = \sqrt{\frac{6h^3}{cG}} \frac{1}{8\pi \mu_e m_e m_p} \frac{\zeta_1}{z_c} \tag{30}\]のようになります。(29)式より、星の全質量は縮退している電子の質量\(m_e\)に依存しないことがわかります。一方で(30)式で求まった半径は\(m_e\)に反比例します。(28)式をある\(z_c\)の解について求めるとき、縮退している気体が電子のような白色矮星である場合と、中性子(質量\(m_n \sim m_p\)のような中性子星とでは、星の全質量は同じであっても半径が大きく異なることがわかります。この例では、中性子星の半径は白色矮星のおよそ\(m_e/ m_n \sim 1/1800\)倍も小さいことがわかります。
数値積分
さて、(28)式を単純に数値的に積分し\(\zeta_1\)を求めれば良いわけですが、計算の途中で\(1/\zeta\)が入ってくることが式からわかります。よって実際に計算を行う際には数値計算は中心\(\zeta=0\)の近傍から始める必要があります。 そのために(28)式を\(\zeta_c=0\)において、\(\varphi(\zeta_c) \equiv \varphi_c = 1, \frac{d\varphi}{d\zeta_0} = 0\)の条件のもとで展開し、その近似式の値から数値計算を行うことにしましょう。(28)式左辺のテイラー展開より
\[\begin{align} \frac{1}{\zeta^2} \frac{d}{d\zeta} \left( \zeta^2 \frac{d \varphi}{d\zeta} \right) &= \frac{1}{\zeta^2} \frac{d}{d\zeta} \left\{ \zeta^2 \frac{d}{d\zeta} \left( 1 + \left. \frac{d\varphi}{d\zeta} \right|_c + \frac{1}{2!} \left. \frac{d^2\varphi}{d\zeta^2} \right|_c \zeta^2 + \frac{1}{3!} \left. \frac{d^3\varphi}{d\zeta^3} \right|_c \zeta^3 + \frac{1}{4!} \left. \frac{d^4\varphi}{d\zeta^4} \right|_c \zeta^4 + \cdots \right) \right\} \notag \\ &= \frac{1}{\zeta^2} \frac{d}{d\zeta} \left(\left. \frac{d^2\varphi}{d\zeta^2} \right|_c \zeta^3 + + \frac{1}{2!} \left. \frac{d^3\varphi}{d\zeta^3} \right|_c \zeta^4 + \frac{1}{3!} \left. \frac{d^4\varphi}{d\zeta^4} \right|_c \zeta^5 + \cdots \right) \notag \\ &= 3 \left. \frac{d^2 \varphi}{d\zeta^2} \right|_c + 2 \left. \frac{d^3 \varphi}{d\zeta^3} \right|_c \zeta + \frac{5}{6} \left. \frac{d^4 \varphi}{d\zeta^4} \right|_c \zeta^2 + \cdots \tag{31} \end{align}\](28)式右辺は
\[\left. \left( \varphi^2 - \frac{1}{z_c^2}\right)^{3/2} \right|_c = \left( 1-\frac{1}{z_c^2}\right)^{3/2}\] \[\left. \frac{d}{d\zeta} \left( \varphi^2 - \frac{1}{z_c^2}\right)^{3/2} \right|_c =\left\{ \frac{3}{2} \left( \varphi^2 - \frac{1}{z_c^2} \right)^{1/2} 2\varphi \frac{d\varphi}{d\zeta}\right\}_c = 0\] \[\begin{aligned} \left. \frac{d^2}{d\zeta^2} \left( \varphi^2 - \frac{1}{z_c^2}\right)^{3/2} \right|_c &= 3 \left\{ \frac{1}{2} \left( \varphi^2 - \frac{1}{z_c^2}\right)^{-1/2} 2\varphi^2 \left( \frac{d\varphi}{d\zeta}\right)^2 + \left( \varphi^2 - \frac{1}{z_c^2}\right)^{1/2} \left( \frac{d\varphi}{d\zeta} \right)^2 + \left( \varphi^2 - \frac{1}{z_c^2}\right)^{1/2} \varphi \frac{d^2 \varphi}{d\zeta^2}\right\}_c \\ &= 3 \left( 1-\frac{1}{z_c^2}\right)^{1/2} \left. \frac{d^2 \varphi}{d\zeta^2} \right|_c \end{aligned}\]などより
\[-\left( 1-\frac{1}{z_c^2} \right)^{3/2} - \frac{3}{2!} \left( 1-\frac{1}{z_c^2} \right)^{1/2} \left. \frac{d^2 \varphi}{d\zeta^2} \right|_c \zeta^2 - \cdots \tag{32}\](31), (32)式において、同じ\(\zeta\)の次数の係数を比べることで
\[\left. \frac{d^2\varphi}{d\zeta^2} \right|_c = -\frac{1}{3} \left( 1-\frac{1}{z_c^2}\right)^{3/2}, \quad \left. \frac{d^3\varphi}{d\zeta^3} \right|_c = 0, \quad \left. \frac{d^4 \varphi}{d\zeta^4} \right|_c = -\frac{9}{5} \left( 1-\frac{1}{z_c^2}\right)^{1/2} \left. \frac{d^2 \varphi}{d\zeta^2} \right|_c = \frac{3}{5} \left( 1-\frac{1}{z_c^2} \right)^2\]を得ます。以上から、求めたかった\(\varphi\)の\(\zeta=\zeta_c = 0\)周りでのテイラー展開は
\[\varphi = 1 - \frac{1}{3\cdot 2!} \left( 1-\frac{1}{z_c^2}\right)^{3/2} \zeta^2 + \frac{3}{5 \cdot 4!} \left( 1-\frac{1}{z_c^2} \right)^2 \zeta^4 + \cdots = 1-\frac{q^3}{6} \zeta^2 + \frac{q^4}{40} \zeta^4 + \cdots \tag{33}\]ここで\(q \equiv (1-1/z_c^2)^{1/2}\)のように置きました。
ここまでくればあとは数値計算を行うだけです。(28)式を
のように変形し、\(\varphi = y_1, d\varphi / d\zeta = y_2\)とおけば
\[\frac{d}{d\zeta} \left( \begin{array}{c} y_1 \\ y_2 \end{array}\right) = \left( \begin{array}{c} y_2 \\ -\frac{2}{\zeta} y_2 - \left( y_1^2 - \frac{1}{z_c^2} \right)^{3/2} \end{array} \right) \tag{33}\]この連立微分方程式を\(z_c\)を入力として数値的に積分すれば、\(\zeta_1\)が求まります。それを(16), (17)式に代入すれば、その\(z_c\)での質量と半径が求まります。 よって様々な\(z_c\)に対してこの計算を実行すれば、質量と半径の関係を表すグラフを描くことができます。ただし\(z_c > z_1 =1\)より、1より大きな値を入力しなければならないことに注意しましょう。 この計算にから\((\mu_e/2)^2 M\)を図示したものを以下に示します。

この図より、有限の質量で半径が0に漸近することがわかります。この限界質量がおよそ
\[M_\mathrm{Ch} \simeq \left( \frac{2}{\mu_e}\right)^2 1.43 M_\odot \tag{34}\]であり、これをチャンドラセカールの限界質量と呼びます。
大雑把な見積もり
以上は精密な計算から求められたものでしたが、最後に大雑把な見積もりから限界質量を算出してみましょう。縮退している電子の個数密度を\(n\)とすると、電子1個が占有する体積はおよそ\(\Delta V \simeq 1/n\)です。よって電子間の平均的な距離は
\[\Delta x = n^{-1/3} \tag{35}\]となります。ここで恒星の全質量を\(M\)、半径を\(R\)、平均分子量を\(\mu_e\)とし、簡単のため、恒星内部は一様密度であるとすると
\[M = \frac{4\pi}{3} R^3 \mu_e m_p n \ \Longrightarrow \ n \simeq \frac{3M}{4\pi R^3 \mu_e m_p} \tag{36}\]となります。電子のエネルギーと運動量の関係は、電子の運動が超相対論的として
\[\varepsilon \simeq cp \tag{37}\]さらに量子力学の不確定性関係より
\[\hbar \simeq \Delta x \Delta p \tag{38}\](35)-(38)式より、恒星内部に存在する縮退した電子の総エネルギーは
\[E_\mathrm{deg} \simeq \frac{4\pi}{3} R^3 n \varepsilon \simeq \frac{M}{\mu_e m_p} cp \simeq \frac{M}{\mu_e m_p} c \frac{\hbar}{\Delta x} \simeq \frac{M}{\mu_e m_p} c \hbar n^{1/3}\]のようになります。途中、\(p \simeq \Delta p\)のように大雑把に考えました。ここにもう一度(36)式を用いれば
\[E_\mathrm{deg} \simeq \left( \frac{3}{4\pi}\right)^{1/3} \left( \frac{M}{\mu_e m_p}\right)^{4/3} \frac{c\hbar}{R} \tag{39}\]となります。エネルギー等分配から、これが重力エネルギーと等しいと考えると
\[\frac{GM}{R} M \simeq \left( \frac{3}{4\pi}\right)^{1/3} \left( \frac{M}{\mu_e m_p}\right)^{4/3} \frac{c\hbar}{R} \ \Longrightarrow \ M \simeq \left( \frac{3}{4\pi}\right)^{1/2} \left( \frac{1}{\mu_e m_p} \right)^2 \left( \frac{c\hbar}{G} \right)^{3/2} \sim \frac{1}{\mu_e^2} M_\odot \tag{40}\]のように、大雑把な見積もりでも大体1太陽質量程度となることがわかります。
参考文献
- 小山勝二, 嶺重慎, “ブラックホールと高エネルギー現象”
- 本間希樹, 東京大学教養学部, “宇宙科学II (電波天文学)” 講義スライド