Table of contents
円筒座標系での磁気流体の運動量保存
運動量保存と一般座標における表示
\[\frac{\partial}{\partial t} (\rho v^i) + \nabla_j \left\{ \left( P + \frac{1}{8\pi} B^2 \right) \delta^{j}_i + \rho v^i v^j - \frac{1}{4\pi} B^i B^j \right\} = F^i \tag{1}\]のように書かれました。ここで\(v^i, B^i\)はそれぞれ流体の速度と磁場の\(i\)成分、\(\rho, P\)は質量密度と圧力、そして右辺の\(F^i\)は外力の\(i\)成分です。左辺第2項は運動量流束テンソル(momentum flux tensor)で
\[\pi^{ij} \equiv \underbrace{\left( P + \frac{1}{8\pi} B^2 \right)}_{\equiv P_\mathrm{gm}} \delta_i^j + \rho v^i v^j - \frac{1}{4\pi} B^i B^j \tag{2}\]です。(1)式を円筒座標系で具体的にどのように書かれるのかを考えましょう。そのためには(1)式をより一般的に、共変微分\(\nabla_\mu\)とエネルギー運動量テンソル\(T^{\mu \nu}\)を用いて
\[\nabla_\mu T^{i\mu} = \nabla_0 T^{i0} + \nabla_j \pi^{ij} = F^i \tag{3}\]のように書きます。つまり一般座標変換に対して、一般相対論で学んだ共変な形で表現するのです。円筒座標系では\(T^{i0}\)は
\[T^{i0} = (\rho \dot{R}, \rho \dot{\varphi}, \rho \dot{z}) = (\rho v_R, \rho \frac{v_\varphi}{R}, \rho v_z) \tag{4}\]となります。\(\pi^{ij}\)はエネルギー運動量テンソルの空間部分で、3次元デカルト座標系での具体的な成分は
\[(\pi^{ij}) = \left( \begin{array}{ccc} P_\mathrm{gm} + \rho v_x^2 - \frac{1}{4\pi} B_x^2 & \rho v_x v_y - \frac{1}{4\pi} B_x B_y & \rho v_x v_z - \frac{1}{4\pi} B_x B_z \\ \rho v_y v_x - \frac{1}{4\pi} B_y B_x & P_\mathrm{gm} + \rho v_y^2 - \frac{1}{4\pi} B_y^2 & \rho v_y v_z - \frac{1}{4\pi} B_y B_z \\ \rho v_z v_x - \frac{1}{4\pi} B_z B_x & \rho v_z v_y - \frac{1}{4\pi} B_z B_y & P_\mathrm{gm} + \rho v_z^2 - \frac{1}{4\pi} B_z^2 \end{array} \right) \equiv \left( \begin{array}{ccc} \pi^{xx} & \pi^{xy} & \pi^{xz} \\ \pi^{yx} & \pi^{yy} & \pi^{yz} \\ \pi^{zx} & \pi^{zy} & \pi^{zz} \end{array}\right) \tag{5}\]のようになります。
\(\pi^{ij}\)の変換
\((x, y, z)\)デカルト座標系から\((R, \varphi, z)\)円筒座標系に移ったときの\((\pi^{ij})\)の成分を、同様に\(\pi^{RR}, \pi^{\varphi z}, \pi^{Rz}\)などのように書くことにします。
デカルト座標で\(\mathbf{v} = (v_x, v_y, v_z), \mathbf{B} = (B_x, B_y, B_z)\)と記述されるベクトルを円筒座標系の成分に書き換えると
のようになります。
円筒座標での\(\pi^{ij}\)を求める前に以下の量を計算しておきましょう。\((x, y, z)\)と\((R, \varphi, z)\)との間には
のような関係があります。これより
\[2 x = 2R \frac{\partial R}{\partial x} \ \Longrightarrow \ \frac{\partial R}{\partial x} = \frac{x}{R} = \cos \varphi \tag{8}\] \[2 y = 2R \frac{\partial R}{\partial y} \ \Longrightarrow \ \frac{\partial R}{\partial y} = \frac{y}{R} = \sin \varphi \tag{9}\] \[\frac{1}{\cos^2 \varphi} \frac{\partial \varphi}{\partial x} = - \frac{y}{x^2} = - \frac{R \sin \varphi}{R^2 \cos^2 \varphi} \ \Longrightarrow \ \frac{\partial \varphi}{\partial x} = - \frac{\sin \varphi}{R} \tag{10}\] \[\frac{1}{\cos^2 \varphi} \frac{\partial \varphi}{\partial y} = \frac{1}{x} = \frac{1}{R \cos \varphi} \ \Longrightarrow \ \frac{\partial \varphi}{\partial y} = - \frac{\cos \varphi}{R} \tag{11}\] \[\frac{\partial R}{\partial z} = \frac{\partial \varphi}{\partial z} = \frac{\partial z}{\partial x} = \frac{\partial z}{\partial y} = 0 \tag{12}\] \[\frac{\partial z}{\partial z} = 1 \tag{13}\]これらを用いて具体的に\(\pi\)の\((R, \varphi, z)\)での形を求めていきましょう。2階のテンソルの成分の変換則は
\[\pi^{i'j'} = \frac{\partial x^{i'}}{\partial x^k} \frac{\partial x^{j'}}{\partial x^\ell} \pi^{k \ell} \tag{14}\]のように与えられるので
\[\begin{align} \pi^{RR} &= \frac{\partial R}{\partial x} \frac{\partial R}{\partial x} \pi^{xx} + \frac{\partial R}{\partial x} \frac{\partial R}{\partial y} \pi^{xy} + \frac{\partial R}{\partial x} \frac{\partial R}{\partial z} \pi^{xz} + \frac{\partial R}{\partial y} \frac{\partial R}{\partial x} \pi^{yx} + \frac{\partial R}{\partial y} \frac{\partial R}{\partial y} \pi^{yy} \notag \\ & \qquad + \frac{\partial R}{\partial y} \frac{\partial R}{\partial z} \pi^{yz} + \frac{\partial R}{\partial z} \frac{\partial R}{\partial x} \pi^{zx} + \frac{\partial R}{\partial z} \frac{\partial R}{\partial y} \pi^{zy} + \frac{\partial R}{\partial z} \frac{\partial R}{\partial z} \pi^{zz} \notag \\ &= \pi^{xx} \cos^2 \varphi + \pi^{xy} \cos \varphi \sin \varphi + \pi^{yx} \sin \varphi \cos \varphi + \pi^{yy} \sin^2 \varphi \notag \\ &= P_\mathrm{gm} + \rho(v_x \cos \varphi + v_y \sin\varphi)^2 - \frac{1}{4\pi} (B_x \cos \varphi + B_y \sin \varphi)^2 = P_\mathrm{gm} + \rho v_R^2 - \frac{1}{4\pi} B_R^2 \tag{15} \end{align}\] \[\begin{align} \pi^{R\varphi} &= \frac{\partial R}{\partial x} \frac{\partial \varphi}{\partial x} \pi^{xx} + \frac{\partial R}{\partial x} \frac{\partial \varphi}{\partial y} \pi^{xy} + \frac{\partial R}{\partial x} \frac{\partial \varphi}{\partial z} \pi^{xz} + \frac{\partial R}{\partial y} \frac{\partial \varphi}{\partial x} \pi^{yx} + \frac{\partial R}{\partial y} \frac{\partial \varphi}{\partial y} \pi^{yy} \notag \\ & \qquad + \frac{\partial R}{\partial y} \frac{\partial \varphi}{\partial z} \pi^{yz} + \frac{\partial R}{\partial z} \frac{\partial \varphi}{\partial x} \pi^{zx} + \frac{\partial R}{\partial z} \frac{\partial \varphi}{\partial y} \pi^{zy} + \frac{\partial R}{\partial z} \frac{\partial \varphi}{\partial z} \pi^{zz} \notag \\ &= - \frac{\cos \varphi \sin \varphi}{R} \pi^{xx} + \frac{\cos^2 \varphi}{R} \pi^{xy} - \frac{\sin^2 \varphi}{R} \pi^{yx} + \frac{\sin \varphi \cos \varphi}{R} \pi^{yy} \notag \\ &= \frac{1}{R} \left\{ \rho v_\varphi (v_x \cos \varphi + v_y \sin \varphi) - \frac{1}{4\pi} B_\varphi (B_x \cos \varphi + B_y \sin \varphi) \right\} = \frac{1}{R} \left( \rho v_R v_\varphi - \frac{1}{4\pi} B_R B_\varphi \right) \tag{16} \end{align}\] \[\begin{align} \pi^{Rz} &= \frac{\partial R}{\partial x} \frac{\partial z}{\partial x} \pi^{xx} + \frac{\partial R}{\partial x} \frac{\partial z}{\partial y} \pi^{xy} + \frac{\partial R}{\partial x} \frac{\partial z}{\partial z} \pi^{xz} + \frac{\partial R}{\partial y} \frac{\partial z}{\partial x} \pi^{yx} + \frac{\partial R}{\partial y} \frac{\partial z}{\partial y} \pi^{yy} \notag \\ & \qquad + \frac{\partial R}{\partial y} \frac{\partial z}{\partial z} \pi^{yz} + \frac{\partial R}{\partial z} \frac{\partial z}{\partial x} \pi^{zx} + \frac{\partial R}{\partial z} \frac{\partial z}{\partial y} \pi^{zy} + \frac{\partial R}{\partial z} \frac{\partial z}{\partial z} \pi^{zz} \notag \\ &= \pi^{xz} \cos \varphi + \pi^{yz} \sin \varphi \notag \\ &= \rho v_z (v_x \cos \varphi + v_y \sin \varphi) - \frac{1}{4\pi} B_z(B_x \cos \varphi + B_y \sin \varphi) = \rho v_R v_z - \frac{1}{4\pi} B_R B_z \tag{17} \end{align}\] \[\begin{align} \pi^{\varphi \varphi} &= \frac{\partial \varphi}{\partial x} \frac{\partial \varphi}{\partial x} \pi^{xx} + \frac{\partial \varphi}{\partial x} \frac{\partial \varphi}{\partial y} \pi^{xy} + \frac{\partial \varphi}{\partial x} \frac{\partial \varphi}{\partial z} \pi^{xz} + \frac{\partial \varphi}{\partial y} \frac{\partial \varphi}{\partial x} \pi^{yx} + \frac{\partial \varphi}{\partial y} \frac{\partial \varphi}{\partial y} \pi^{yy} \notag \\ & \qquad + \frac{\partial \varphi}{\partial y} \frac{\partial \varphi}{\partial z} \pi^{yz} + \frac{\partial \varphi}{\partial z} \frac{\partial \varphi}{\partial x} \pi^{zx} + \frac{\partial \varphi}{\partial z} \frac{\partial \varphi}{\partial y} \pi^{zy} + \frac{\partial \varphi}{\partial z} \frac{\partial \varphi}{\partial z} \pi^{zz} \notag \\ &= \frac{\sin^2 \varphi}{R^2} \pi^{xx} - \frac{\sin \varphi \cos \varphi}{R^2} \pi^{xy} - \frac{\cos \varphi \sin \varphi}{R^2} \pi^{yx} + \frac{\cos^2 \varphi}{R^2} \pi^{yy} \notag \\ &= \frac{1}{R^2} \left\{ P_\mathrm{gm} + (v_x \sin \varphi - v_y \cos \varphi)^2 - \frac{1}{4\pi} (B_x \sin \varphi - B_y \cos \varphi)^2\right\} = \frac{1}{R^2} \left( P_\mathrm{gm} + \rho v_\varphi^2 - \frac{1}{4\pi} B_\varphi^2 \right) \tag{18} \end{align}\] \[\begin{align} \pi^{\varphi z} &= \frac{\partial \varphi}{\partial x} \frac{\partial z}{\partial x} \pi^{xx} + \frac{\partial \varphi}{\partial x} \frac{\partial z}{\partial y} \pi^{xy} + \frac{\partial \varphi}{\partial x} \frac{\partial z}{\partial z} \pi^{xz} + \frac{\partial \varphi}{\partial y} \frac{\partial z}{\partial x} \pi^{yx} + \frac{\partial \varphi}{\partial y} \frac{\partial z}{\partial y} \pi^{yy} \notag \\ &\qquad + \frac{\partial \varphi}{\partial y} \frac{\partial z}{\partial z} \pi^{yz} + \frac{\partial \varphi}{\partial z} \frac{\partial z}{\partial x} \pi^{zx} + \frac{\partial \varphi}{\partial z} \frac{\partial z}{\partial y} \pi^{zy} + \frac{\partial \varphi}{\partial z} \frac{\partial z}{\partial z} \pi^{zz} \notag \\ &= - \frac{\sin \varphi}{R} \pi^{xz} + \frac{\cos \varphi}{R} \pi^{yz} \notag \\ &= \frac{1}{R} \left( \rho v_\varphi v_z - \frac{1}{4\pi} B_\varphi B_z\right) \tag{19} \end{align}\]\(\pi^{zz}\)は変わらずそのままであること、そして
\[\pi^{\varphi R} = \frac{\partial \varphi}{\partial x^k} \frac{\partial R}{\partial x^\ell} \pi^{k \ell} = \frac{\partial R}{\partial x^\ell} \frac{\partial \varphi}{\partial x^k} \pi^{k \ell} = \frac{\partial R}{\partial x^k} \frac{\partial \varphi}{\partial x^\ell} \underbrace{\pi^{\ell k}}_{(5)より対称テンソル} = \pi^{R\varphi} \tag{20}\]などより、これらをまとめて
\[(\pi^{ij}) = \left( \begin{array}{ccc} \pi^{RR} & \pi^{R\varphi} & \pi^{Rz} \\ \pi^{\varphi R} & \pi^{\varphi \varphi} & \pi^{\varphi z} \\ \pi^{zR} & \pi^{z\varphi} & \pi^{zz} \end{array}\right) = \left( \begin{array}{ccc} P_\mathrm{gm} + \rho v_R^2 - \frac{1}{4\pi} B_R^2 & \frac{1}{R} \left( \rho v_R v_\varphi - \frac{1}{4\pi} B_R B_\varphi \right) & v_R v_z - \frac{1}{4\pi} B_R B_z \\ \frac{1}{R} \left( \rho v_\varphi v_R - \frac{1}{4\pi} B_\varphi B_R \right) & \frac{1}{R^2} \left( P_\mathrm{gm} + \rho v_\varphi^2 - \frac{1}{4\pi} B_\varphi^2 \right) & \frac{1}{R} \left( \rho v_\varphi v_z - \frac{1}{4\pi} B_\varphi B_z\right) \\ \rho v_z v_R - \frac{1}{4\pi} B_z B_R & \frac{1}{R} \left( \rho v_z v_\varphi - \frac{1}{4\pi} B_z B_\varphi \right) & P_\mathrm{gm} + \rho v_z^2 - \frac{1}{4\pi} B_z^2 \end{array} \right) \tag{21}\]
テンソルの発散
(21)式を(3)式に代入して具体的に計算します。このとき、(3)式の\(\nabla_j \pi^{ij}\)部分はただの発散ではなく、テンソルの発散です。よってこの部分はちゃんとテンソルの共変微分を考える必要があります。よって、正しくは
\[\nabla_0 T^{i0} + \nabla_j \pi^{ij} = \frac{\partial}{\partial t} T^{i0} + \partial_j \pi^{ij} + \Gamma^i_{\ell j} \pi^{\ell j} + \Gamma^j_{\ell j} \pi^{i\ell} = F^i \tag{22}\]を計算します。
第1項の共変微分をただの時間偏微分にしたのは、今の場合には座標基底が時間に依存しないためです。これは具体的にクリストッフェル記号を計算することでも確かめられます。
結局、時間に関係する添字を持つクリストッフェル記号は全て0となります。
クリストッフェル記号は
\[\Gamma^i_{jk} = \frac{1}{2} g^{i\ell} (g_{\ell j, k} + g_{\ell k, j} - g_{jk, \ell})\]です。そして円筒座標系のメトリックテンソルの成分は
\[g_{RR} = g_{zz} = 1, \quad g_{\varphi \varphi} = R^2, \quad g^{RR} = g^{zz} = 1, \quad g^{\varphi \varphi} = \frac{1}{R^2}\]です。これ以外は0です。またその成分の微分は
\[g_{\varphi \varphi, R} = 2R\]以外は0であることもわかります。これらより
\[\Gamma^{R}_{\varphi \varphi} = \frac{1}{2} g^{R \ell} (g_{\ell \varphi, \varphi} + g_{\ell \varphi, \varphi} - g_{\varphi \varphi, \ell}) \underbrace{=}_{\ell = Rのみ} - R \tag{23}\] \[\Gamma^\varphi_{R \varphi} = \frac{1}{2} g^{\varphi \ell} (g_{\ell R, \varphi} + g_{\ell \varphi, R} - g_{R \varphi, \ell}) \underbrace{=}_{\ell = \varphi のみ} \frac{1}{2} \frac{1}{R^2} 2R = \frac{1}{R} \tag{24}\] \[\Gamma^\varphi_{\varphi R} = \Gamma^\varphi_{R \varphi} = \frac{1}{R} \tag{25}\]これ以外の添字の組合せを持つクリトッフェル記号は全て0です。
(4), (21)-(25)式を用いて、最終的な円筒座標系での運動量保存を導きましょう。まずは\(R\)成分です。
\[\begin{align} &\frac{\partial}{\partial t} (\rho v_R) + \partial_j \pi^{Rj} + \Gamma^R_{\ell j} \pi^{\ell j} + \Gamma^j_{\ell j} \pi^{R \ell} = \frac{\partial}{\partial t} (\rho v_R) + \partial_R \pi^{RR} + \partial_\varphi \pi^{R \varphi} + \partial_z \pi^{Rz} - R \pi^{\varphi \varphi} + \frac{1}{R} \pi^{RR} \notag \\ &= \frac{\partial}{\partial t} (\rho v_R) + \frac{\partial}{\partial R} \left( P_\mathrm{gm} + \rho v_R^2 - \frac{1}{4\pi} B_R^2 \right) + \frac{1}{R} \frac{\partial}{\partial \varphi} \left( \rho v_R v_\varphi - \frac{1}{4\pi} B_R B_\varphi \right) \notag \\ & \qquad + \frac{\partial}{\partial z} \left( \rho v_R v_z - \frac{1}{4\pi} B_R B_z \right) + \frac{1}{R} \left\{ \left( \rho v_R^2 - \frac{1}{4\pi} B_R^2\right) - \left( \rho v_\varphi^2 - \frac{1}{4\pi} B_\varphi^2\right)\right\} \tag{26} \end{align}\]続いて\(\varphi\)成分です。
\[\begin{align} &\frac{\partial}{\partial t} \left( \rho \frac{v_\varphi}{R} \right) + \partial_j \pi^{\varphi j} + \Gamma^\varphi_{\ell j} \pi^{\ell j} + \Gamma^j_{\ell j} \pi^{\varphi \ell} \notag \\ &= \frac{1}{R} \frac{\partial}{\partial t} (\rho v_\varphi) + \partial_R \pi^{\varphi R} + \partial_\varphi \pi^{\varphi \varphi} + \partial_z \pi^{\varphi z} + \frac{1}{R} \pi^{\varphi R} + \frac{1}{R} \pi^{R \varphi} + \frac{1}{R} \pi^{\varphi R} \notag \\ &= \frac{1}{R} \left\{ \frac{\partial}{\partial t}(\rho v_\varphi) + \frac{\partial }{\partial R} \left( \rho v_\varphi v_R - \frac{1}{4\pi} B_\varphi B_R \right) + \frac{1}{R} \frac{\partial}{\partial \varphi} \left( P_\mathrm{gm} + \rho v_\varphi^2 - \frac{1}{4\pi} B_\varphi^2 \right) \right. \notag \\ &\qquad \left. + \frac{\partial}{\partial z} \left( \rho v_\varphi v_z - \frac{1}{4\pi} B_\varphi B_z \right) + \frac{2}{R} \left( \rho v_\varphi v_R - \frac{1}{4\pi} B_\varphi B_R \right)\right\} \tag{27} \end{align}\]最後に\(z\)成分です。
\[\begin{align} &\frac{\partial}{\partial t} (\rho v_z) + \partial_j \pi^{zj} + \Gamma^z_{\ell j} \pi^{\ell j} + \Gamma^j_{\ell j} \pi^{z\ell} = \frac{\partial}{\partial t} (\rho v_z) + \partial_R \pi^{zR} + \partial_\varphi \pi^{z\varphi} + \partial_z \pi^{zz} + \frac{1}{R} \pi^{zR} \notag \\ &= \frac{\partial}{\partial t} (\rho v_z) + \frac{\partial}{\partial R} \left( \rho v_z v_R - \frac{1}{4\pi} B_z B_R\right) + \frac{1}{R} \frac{\partial}{\partial \varphi} \left( \rho v_z v_\varphi - \frac{1}{4\pi} B_z B_\varphi \right) \notag \\ & \qquad + \frac{\partial}{\partial z} \left( P_\mathrm{gm} + v_z^2 - \frac{1}{4\pi} B_z^2 \right) + \frac{1}{R} \left( \rho v_z v_R - \frac{1}{4\pi} B_z B_R\right) \tag{28} \end{align}\]以上より
\[\begin{align} &\frac{\partial}{\partial t} \left( \begin{array}{c} \rho v_R \\ \rho v_\varphi \\ \rho v_z \end{array}\right) + \frac{\partial}{\partial R} \left( \begin{array}{c} \rho v_R^2 - \frac{1}{4\pi} B_R^2 + P_\mathrm{gm} \\ \rho v_\varphi v_R - \frac{1}{4\pi} B_\varphi B_R \\ \rho v_z v_R - \frac{1}{4\pi} B_z B_R \end{array}\right) + \frac{1}{R} \frac{\partial}{\partial \varphi} \left( \begin{array}{c} \rho v_R v_\varphi - \frac{1}{4\pi} B_R B_\varphi \\ \rho v_\varphi^2 - \frac{1}{4\pi} B_\varphi^2 + P_\mathrm{gm} \\ \rho v_z v_\varphi - \frac{1}{4\pi} B_z B_\varphi \end{array}\right) \notag \\ & \qquad + \frac{\partial}{\partial z} \left( \begin{array}{c} \rho v_R v_z - \frac{1}{4\pi} B_R B_z \\ \rho v_\varphi v_z - \frac{1}{4\pi} B_\varphi B_z \\ \rho v_z^2 - \frac{1}{4\pi} B_z^2 + P_\mathrm{gm} \end{array}\right) + \left( \begin{array}{c} \frac{1}{R} \left\{ \left( \rho v_R^2 - \frac{1}{4\pi} B_R^2 \right) - \left( \rho v_\varphi^2 - \frac{1}{4\pi} B_\varphi^2 \right) \right\}\\ \frac{2}{R} \left( \rho v_\varphi v_R - \frac{1}{4\pi} B_\varphi B_R \right) \\ \frac{1}{R} \left( \rho v_z v_R - \frac{1}{4\pi} B_z B_R \right) \end{array}\right) = \left( \begin{array}{c} F_R \\ F_\varphi \\ F_z \end{array} \right) \tag{29} \end{align}\]保存系にする
グリッドを用いた(オイラー的な)磁気流体数値計算においては、グリッドに区切られたセル中心で物理量を定義します。隣のセルから入ってくる物理量を、受け取る側のセルは正しく受け取る必要があります。そのために基礎方程式を、\(\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \mathbf{v}) = 0\)のような保存系に近い形で書いておきましょう。まずは(29)式の\(R\)方向成分です。
\[\frac{1}{R} \frac{\partial}{\partial R} \left\{ R \left( \rho v_R^2 - \frac{1}{4\pi} B_R^2\right)\right\} = \frac{1}{R} \left( \rho v_R^2 - \frac{1}{4\pi} B_R^2\right) + \frac{\partial}{\partial R} \left( \rho v_R^2 - \frac{1}{4\pi} B_R^2\right)\]と、円筒座標系での発散公式
\[\nabla \cdot \mathbf{A} = \frac{1}{R} \frac{\partial}{\partial R} (R A_R) + \frac{1}{R} \frac{\partial A_\varphi}{\partial \varphi} + \frac{\partial A_z}{\partial z} \tag{30}\]を用いると
\[\frac{\partial}{\partial t} (\rho v_R) + \nabla \cdot \left( \rho v_R \mathbf{v} - \frac{1}{4\pi} B_R \mathbf{B} + P_\mathrm{gm} \mathbf{e}_R \right) = \frac{1}{R} \left( \rho v_\varphi^2 - \frac{1}{4\pi} B_\varphi^2 + P_\mathrm{gm} \right) + F_R \tag{31}\]のようになります。
次に\(\varphi\)方向成分を計算しましょう。(29)式の\(\varphi\)方向成分では、円筒座標系に移ったことによるコリオリ力のような項が出てきています。これを整理するために両辺に\(R\)をかけて、単位体積あたりの角運動量の\(z\)成分\(L_z = R \rho v_\varphi\)の保存則の式に書き換えます。
これと
\[\frac{\partial}{\partial R} \left\{ R \left( \rho v_\varphi v_R - \frac{1}{4\pi} B_\varphi B_R \right)\right\} = \left( \rho v_\varphi v_R - \frac{1}{4\pi} B_\varphi B_R \right) + R \frac{\partial}{\partial R} \left( \rho v_\varphi v_R - \frac{1}{4\pi} B_\varphi B_R \right)\]より
\[\begin{aligned} &\frac{\partial L_z}{\partial t} + \frac{\partial}{\partial R} \left( L_z v_R - \frac{R}{4\pi} B_\varphi B_R\right) + \frac{1}{R} \frac{\partial}{\partial \varphi} \left( L_z v_\varphi - \frac{R}{4\pi} B_\varphi^2 \right) + \frac{\partial}{\partial z} \left( L_z v_z - \frac{R}{4\pi} B_\varphi B_z\right) \\ &\qquad + \frac{1}{R} \left( L_z v_R - \frac{R}{4\pi} B_R B_\varphi \right) = R F_\varphi \end{aligned}\]これにさらに
\[\frac{1}{R} \frac{\partial}{\partial R} \left\{ R \left( L_z v_R - \frac{R}{4\pi} B_\varphi B_R \right)\right\} = \frac{1}{R} \left( L_z v_R - \frac{R}{4\pi} B_\varphi B_R\right) + \frac{\partial}{\partial R} \left( L_z v_R - \frac{R}{4\pi} B_\varphi B_R\right)\]と円筒座標系での発散(30)式を用いれば
\[\frac{\partial L_z}{\partial t} + \nabla \cdot \left( L_z \mathbf{v} - \frac{R}{4\pi} B_\varphi \mathbf{B} + R P_\mathrm{gm} \mathbf{e}_\varphi \right) = R F_\varphi \tag{32}\]のようになります。同様に\(z\)方向についても整理すると
\[\frac{\partial}{\partial t} (\rho v_z) + \nabla \cdot \left( \rho v_z \mathbf{v} - \frac{1}{4\pi} B_z \mathbf{B} + P_\mathrm{gm} \mathbf{e}_z \right) = F_z \tag{33}\]よって(31), (32), (33)式を用いて、数値計算を行います。
源泉項の意味
途中で出てきた(31)式の源泉項の意味を考えてみましょう。\(\rho v_\varphi^2 / R\)は遠心力を表します。そして\(\frac{1}{4\pi} \frac{B_\varphi^2}{R}\)は磁気張力によるものです。これは下図のようにして理解することができます。
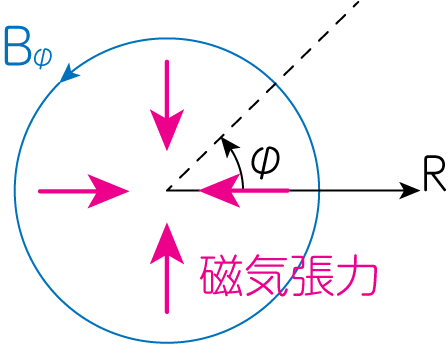
\(\varphi\)成分のみを持つ円形磁場を考えると、この円形磁場により発生する磁気張力は原点に向かうような向きになります。このことから、この項の係数がマイナスとなっています。
他の方法
運動量保存則の式から直接導くのではなく、運動方程式の形
\[\rho \left\{ \frac{\partial \mathbf{v}}{\partial t} + (\mathbf{v} \cdot \nabla) \mathbf{v} \right\} = - \nabla P_\mathrm{gm} + \frac{1}{4\pi} (\mathbf{B} \cdot \nabla) \mathbf{B} + \mathbf{F}\]を直接、式変形することで得ることもできます。このとき、円筒座標系の磁気張力や移流項の計算に注意します。例えば
\[(\mathbf{B} \cdot \nabla) B_R = B_R \frac{\partial B_R}{\partial R} + \frac{B_\varphi}{R} \frac{\partial B_R}{\partial \varphi} - \frac{B_\varphi^2}{R} + B_z \frac{\partial B_R}{\partial z}\]のようになります。
参考文献
[1] 富阪幸治, 花輪知幸, 牧野淳一郎, “シミュレーション天文学”
[2] Chandrasekhar, “Hydrodynamic and Hydromagnetic Stability”
[3] Skinner & Ostriker, 2010, “The Athena Astrophysical MHD Code in Cylindrical Geometry”
[4] Mignone et al., “PLUTO: A Numerical Code for Computational Astrophysics”