Table of contents
動的摩擦 (Dynamical friction)
2体問題から導出される2体緩和を多粒子系に発展させることで、重力多体系の緩和時間を求めることができました。 ここではそれをさらに応用し、周囲の天体より重たい天体にかかる動的摩擦を求めてみましょう。
動的摩擦の直感的理解
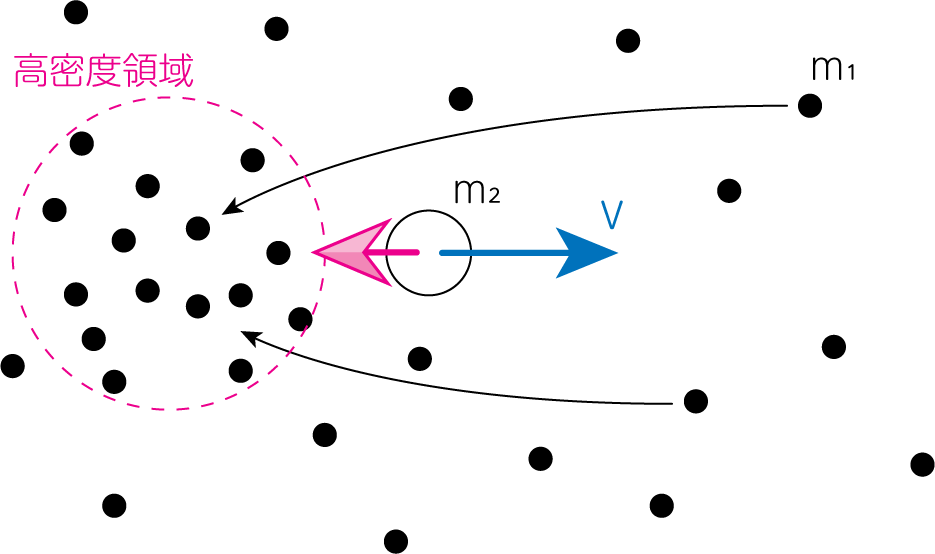
たとえば、質量\(m_1\)の恒星からなる星団中に、\(m_2\)の別の天体が新たに入ってきたとしましょう。このとき、新たに入ってきたこの天体は周囲よりも重たい\((m_2 > m_1)\)とします。 この天体が星団中を直進する間に、周囲の恒星はこの天体と重力相互作用を起こし、下図のようにその軌道を曲げて飛んでいきます。 すると重たい天体の後方に、周囲よりも高密度な領域が発生します。この高密度領域からの重力が天体にブレーキをかけます。これが動的摩擦のイメージです。
解析的な導出
それでは数式を用いてこれを導出してみましょう。2体緩和で求めた\(v_\perp\)より、初速度に平行な成分\(v_\parallel\)を求めてみましょう。
\[v^2 = v_\parallel^2 + v_\perp^2 \ \Longrightarrow \ v_\parallel^2 = v^2 - \frac{4 v^6 b^2}{G^2 M^2} \left( 1+ \frac{v^4 b^2}{G^2 M^2}\right)^{-2} = v^2 \left( \frac{1- \frac{v^4 b^2}{G^2 M^2}}{1 + \frac{v^4 b^2}{G^2 M^2}} \right)^2 \tag{1}\]双曲線軌道で無限遠方に飛び去ることを考えると、\(v_\parallel > 0\)であること、そして2体緩和のときと同様に
\[\frac{v^2}{b} \gg \frac{GM}{b^2} \ \Longrightarrow \ \frac{v^4 b^2}{GM} \gg 1 \tag{2}\]という仮定のもとで式変形することを考えましょう。すると\(1-\frac{v^4 b^2}{G^2 M^2} < 0\)となるため、(1)式の2乗を外すときには
\[v_\parallel = v \frac{\frac{v^4 b^2}{G^2 M^2} - 1}{1 + \frac{v^4 b^2}{G^2 M^2}} \tag{3}\]のようになります。ここから、初速度に平行な成分の速度の変化分は
\[\delta v_\parallel = v_\parallel - v = - \frac{2v} {1 + \frac{v^4 b^2}{G^2 M^2}} \tag{4}\]と計算されます。これまでは天体2が静止している系(相対座標系)で考えてきました。ここからはどちらも運動している慣性系での運動を考えていきます。
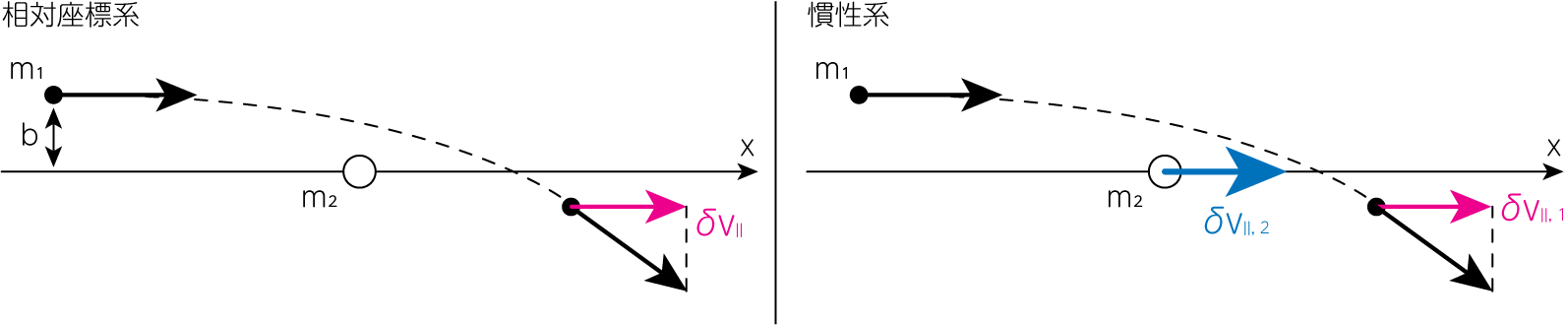
上図のように天体1, 2の\(x\)方向の速度変化分をそれぞれ\(\delta v_{\parallel, 1}, \delta v_{\parallel, 2}\)とすると
\[\delta v_\parallel = \delta v_{\parallel, 1} - \delta v_{\parallel, 2} \tag{5}\]となります。さらに天体1, 2の質量をそれぞれ\(m_1, m_2\)とすると、\(x\)方向の運動量保存則より
\[m_1 \delta v_{\parallel, 1} + m_2 \delta v_{\parallel, 2} = 0 \ \Longrightarrow \ \delta v_{\parallel, 2} = - \frac{m_1}{m_1 + m_2} \delta v_\parallel \tag{6}\]です。2体問題の定式化より、\(M = m_1 + m_2\)から
\[\delta v_{\parallel, 2} = \frac{2 m_1 v}{M \left( 1 + \frac{v^4 b^2}{G^2 M^2}\right)} \tag{7}\]となります。天体1と衝突している\(\Delta t\)秒の間に、天体2が受ける力は
\[f \simeq m_2 \frac{\delta v_{\parallel, 2}}{\Delta t} = \frac{2 m_1 m_2 v}{M \Delta t} \frac{1}{1 + \frac{v^4 b^2}{G^2 M^2}} \tag{8}\]となります。これはインパクトパラメータ\(b\)で衝突する天体1から受ける力です。これを多粒子に拡張しましょう。 2体緩和のときと同様に、無限遠から速度\(v\)の一定速度で多粒子が入射する場合を考えます。 入射してくる天体の質量は全て\(m_1\)とし、天体の個数密度は\(n\)とすると、\(\Delta t\)の間にインパクトパラメータが\(b \sim b+db\)で入射してくる天体数は\(2\pi b db v \Delta t n\)です。 するとインパクトパラメータが\(b \sim b + db\)の範囲にある粒子とのすれ違いにより受ける力を全て足し合わせたものは
\[F(b) db = \frac{4 \pi n m_1 m_2 v^2}{M} \frac{b}{1 + \frac{v^4 b^2}{G^2 M^2}} db \tag{9}\]のように表されるので、これを考えられる\(b\)の範囲で積分すれば、あらゆるインパクトパラメータですれ違う粒子から受ける力の合計となります。
\[F_\mathrm{total} = \frac{4 \pi n m_1 m_2 v^2}{M} \int_{b_\mathrm{min}}^{b_\mathrm{max}} \frac{b}{1 + \frac{v^4 b^2}{G^2 M^2}} db \tag{10}\]\(a \equiv v^4 / G^2 M^2\)と置くと、この積分は
\[\int_{b_\mathrm{min}}^{b_\mathrm{max}} \frac{b}{1 + a b^2} db = \frac{1}{2a} \int_{b_\mathrm{min}}^{b_\mathrm{max}} \frac{2a b}{1 + a b^2} db = \frac{1}{2a} [\log \vert 1 + a b^2\vert ]_{b_\mathrm{min}}^{b_\mathrm{max}} = \frac{1}{2a} \log \left( \frac{1 + a b_\mathrm{max}^2}{1 + a b_\mathrm{min}^2}\right)\]のように計算されるので、最終的に
\[F_\mathrm{total} = \frac{2\pi n m_1 m_2 G^2 M}{v^2} \log \left( \frac{b_\mathrm{max}^2 + \frac{G^2 M^2}{v^4}}{b_\mathrm{min}^2 + \frac{G^2 M^2}{v^4}}\right) \tag{11}\]となります。このように\(x\)軸負の方向に速度\(v\)で動いている天体2に対して、正の方向(すなわち運動と反対方向)に力が加わることから、天体2は減速を受けることがわかります。 ここで背景として存在する多粒子系の質量密度を\(\rho = n m_1\)と書き、さらに\(m_2 \gg m_1\)のように考えれば、\(M = m_1 + m_2 \simeq m_2\)より
\[F_\mathrm{DF} = \frac{2\pi G^2 m_2^2 \rho}{v^2} \log \left( \frac{b_\mathrm{max}^2 + \frac{G^2 m_2^2}{v^4}}{b_\mathrm{min}^2 + \frac{G^2 m_2^2}{v^4}}\right) \tag{12}\]のように書き直されます。
応用: 銀河の合体 (galaxy merger)
宇宙に存在する銀河は、その進化の過程で多数の合体を経験していることが知られています。 自分自身と同程度の質量を持つ銀河との合体(major merger)から自分自身より質量の小さい銀河との合体(minor merger)まで、その合体の様相は様々です。 ここでは下図のように、質量の大きな銀河と質量の小さな銀河との合体を考えてみましょう。
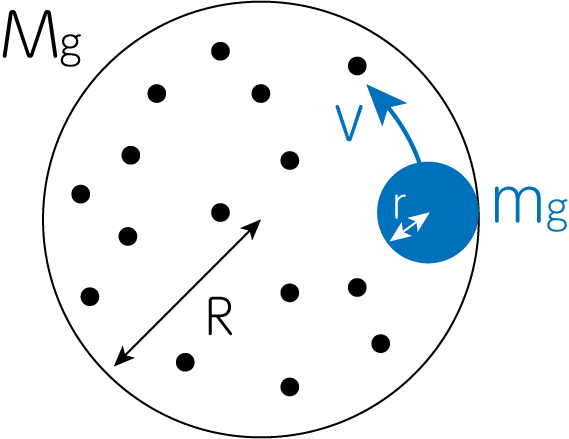
大きな銀河の質量を\(M_g\)、小さな銀河の質量を\(m_g\)とします。 ここで\(M_g \gg m_g\)としますが、大きな銀河を構成する1つ1つの天体の質量は\(m_g\)よりも十分小さく、(12)式が適用できるものとします。 小さな銀河が大きな銀河の中に飲み込まれると考えると、(12)式で現れた背景の質量密度は
\[\rho \simeq \frac{M_g}{\frac{4\pi}{3} R^3} \tag{13}\]のようになります。ここで大きな銀河の半径を\(R\)、簡単のため銀河は球対称で一様な質量密度をしているとしました。小さな銀河は大きな銀河の外縁をかすめるように突入したとすると、小さな銀河の速度は大雑把に遠心力と重力の釣り合いより
\[\frac{v^2}{R} \simeq \frac{GM_g}{R^2} \ \Longrightarrow \ v \simeq \sqrt{\frac{GM_g}{R}} \tag{14}\]と求まります。インパクトパラメータを考えると、大きな銀河の半径より\(b_\mathrm{max} \simeq R\)です。 さらに小さな銀河の半径を\(r\)とすれば、\(b_\mathrm{min} \simeq r\)と考えることができるので、これらを(12)式に代入します。このとき\(M_g \gg m_g\)より、対数の中身を
\[\frac{R^2 + \frac{m_g^2 R^2}{M_g^2}}{r^2 + \frac{m_g^2 R^2}{M_g^2}} \simeq \frac{R^2}{r^2 + \frac{m_g^2 R^2}{M_g^2}} = \frac{1}{\left( \frac{r}{R}\right)^2 + \left( \frac{m_g}{M_g}\right)} \simeq \left( \frac{R}{r} \right)^2\]のように近似すれば
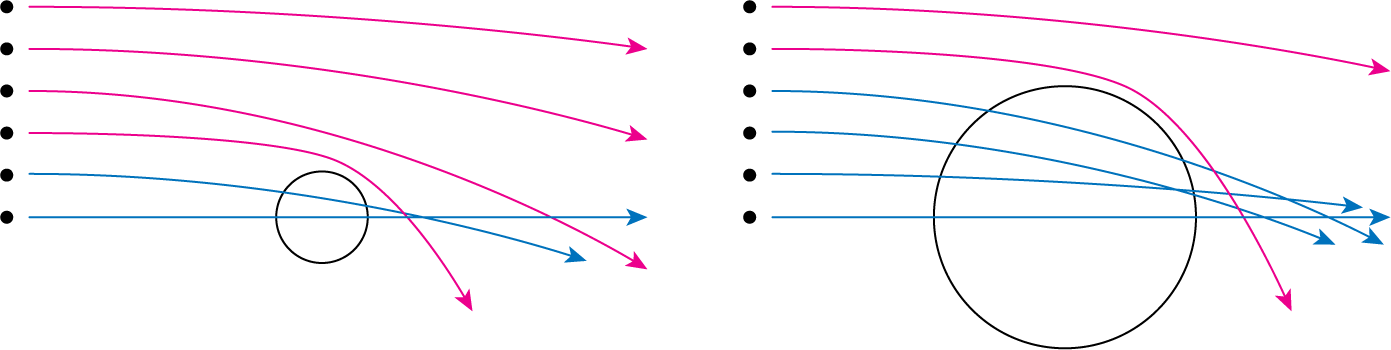
\[F_\mathrm{DF} \simeq \frac{3 G m_g^2}{R^2} \log\left( \frac{R}{r}\right) \tag{15}\]となります。(15)式を見ると、小さな銀河の半径\(r\)が大きいほど、この銀河にかかる力\(F_\mathrm{DF}\)が弱くなることがわかります。 これは大きな半径ほど、双曲線軌道で飛び去る背景粒子が少なくなるためです。 下図のように、小さな銀河の外側を通過する粒子(マゼンタの軌跡)は、これまで考えてきたような双曲線軌道を描き、これが主に動的摩擦を引き起こす要因となります。 しかし小さな銀河の内側を通過する粒子(青色の軌跡)は、外側をかすめる軌跡よりも軌道を曲げることはありません。 これは銀河が無衝突系であり、内側を通過する粒子に働く重力は、その粒子よりも内側部分に存在する質量による重力しか働かないためです。
合体が完了するまでにかかるおおよその時間を\(t_\mathrm{merge}\)としましょう。

ここで合体完了時間とは、小さな銀河の角運動量が全て失われ、小さな銀河が大きな銀河の中心に落ち込むまでにかかる時間とします。すると
\[\frac{m_g v R}{t_\mathrm{merge}} - R F_\mathrm{DF} \sim 0 \tag{16}\]のように書くことができます。ここで第一項は単位時間あたりの角運動量変化、第二項は動的摩擦により働くトルク\((\mathbf{N} = \mathbf{r} \times \mathbf{F})\)です。 この式と(15)式から計算される\(t_\mathrm{merge}\)と、crossing timescale \(t_\mathrm{cross}\)の比を取ると
\[\frac{t_\mathrm{merge}}{t_\mathrm{cross}} \simeq \frac{m_g v}{F_\mathrm{DF}} \frac{v}{R} = \frac{R v^2}{3 G m_g \log \left( \frac{R}{r} \right)} \underbrace{=}_{(14)} \frac{\frac{M_g}{m_g}}{3 \log \left( \frac{R}{r} \right)} \tag{17}\]となります。 分子に\(M_g/ m_g\)のように、合体する銀河の質量比が入っています。(17)式からもわかるように\(m_g \simeq M_g\)のとき、すなわち合体する2つの銀河が等しいとき、合体にかかる時間は最小となります。 仮に\(m_g = 1 M_\odot\)、すなわちこれまで小さな銀河と言ってきたものを、恒星一つからなる系だとしましょう。 するとこれは大きな銀河に恒星が一つ飛び込んだときに、それが銀河中心に落ちるまでの時間を計算していることになります。 銀河がすでに多数の恒星から成り立つ系であることからわかるように、この合体にかかる時間はとても大きく、無限大の時間がかかると言っても差し支えないことがわかります。
天の川銀河の周囲には、球状星団や矮小銀河が存在することが知られています。天の川銀河の総質量はおよそ\(10^{12} M_\odot\)なのに対し、球状星団の質量は\(10^5 M_\odot\)、そして矮小銀河は\(10^7 M_\odot\)などの質量を持ちます。 長い目で見ればこれらも天の川銀河中心に落ち込んでいくことがわかります。