Table of contents
輻射によるエネルギーの流れ
恒星内部の静水圧平衡の式を閉じさせ、内部構造を得るためには、温度分布を記述する式が必要でした。 この式を得るには、エネルギーの発生と輸送を考えなければなりません。 温度勾配が存在すると、熱エネルギーは温度の高い場所から低い場所へと運ばれます。 恒星の中で重要な働きをするエネルギー輸送には、輻射・電子伝導・対流の3つがあります。
ここでは輻射、すなわち光子によるエネルギー輸送について考えましょう。
輻射の強度とエネルギー流束
恒星の中心を中心とするある球面上の、単位面積を通過する光のエネルギーを考えます。
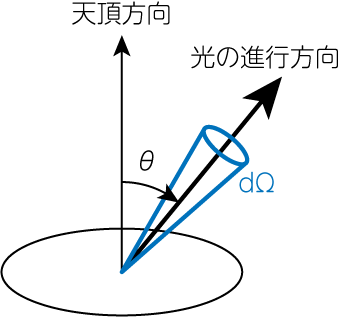
その面の天頂方向からの角度が\(\theta\)の方向の微小立体角\(d\Omega\)内を、単位時間あたりに通過する(振動数が\(\nu \sim \nu + d\nu\)の間にある)輻射のエネルギーは、振動数\(\nu\)の光の強度\(I_\nu (r, \theta)\)を用いて
\[I_\nu (r, \theta) \cos \theta d\nu d\Omega \tag{5.1.1}\]と表されます。 これが光の強度 (intensity) \(I_\nu\)の定義です。 \(I_\nu\)はある方向に、その方向に垂直な単位面積を通過して、単位立体角・単位時間あたりに流れる光のエネルギーを表す \(I_\nu \geq 0\)となるような量です。 (5.1.1)式で\(\cos \theta\)がかかっているのは、光が斜めに入射することで有効面積が減少するためです。 \(\cos \theta\)により、内向きに通過する光\(\pi / 2 \leq \theta \leq \pi\)に対して、(5.1.1)式は負の値を持つこともできます。
(5.1.1)式を全立体角で積分すると、単位時間・単位面積あたりに正味通過するエネルギー、すなわちエネルギーフラックス(流束)を得ることができます。
ここで\(F_\nu\)は、単位振動数あたりのエネルギー流束を表します。 \(I_\nu\)が\(\theta\)に依存しない(isotopic, 等方的)場合、内向きと外向きの流れが同量であるため、\(F_\nu =0\)となります。 恒星内部では、等方的な状態からのわずかなズレによって、輻射が外側に染み出す状態になっています。
輻射エネルギー密度
光は光速度\(c\)で進むため、ある方向の微小立体角\(d\Omega\)内の振動数\(\nu\)の輻射エネルギー密度波\(\frac{I_\nu d\Omega}{c}\)で与えられます。 ある場所での輻射エネルギー密度\(u_\nu\)は、あらゆる方向に進む光のエネルギーを足し合わせたものなので
\[u_\nu = \frac{1}{c} \int_{4\pi} I_\nu (\theta, \varphi) d\Omega = \frac{4\pi}{c} J_\nu \tag{5.1.3}\]のように表されます。 ここで\(J_\nu\)は\(I_\nu (\theta \varphi)\)を方向に対して平均した量で、光の平均強度(mean intensity)と呼ばれ
\[J_\nu \equiv \frac{1}{4\pi} \int_{4\pi} I_\nu (\theta, \varphi) d\Omega \tag{5.1.4}\]のように定義されます。 恒星内部では、輻射とガスの間で局所熱平衡(LTE)が良い近似で成り立っているため、輻射はほとんど黒体輻射で記述することができます。 この場合、\(u_\nu d\nu = \frac{4\pi}{c} B_\nu d\nu\)と(5.1.3)式を比較することで
\[J_\nu \approx B_\nu (T) = \frac{2h\nu^3}{c^2} \frac{1}{\exp(h\nu / (k_B T)) -1} \tag{5.1.5}\]のようになっているとわかります。
輻射圧
ある面にかかる圧力は、その面に垂直な方向の運動量流束です。 光の運動量は、エネルギーを光速度\(c\)で割ったものです。 よって振動数\(\nu \sim \nu + d\nu\)の間の光による圧力\(P_\mathrm{rad, \nu} d\nu\)は
\[P_\mathrm{rad, \nu} = \frac{d\nu}{c} \int_{4\pi} I_\nu (r, \theta) \cos^2 \theta d\Omega \tag{5.1.6}\]のように表されます。 エネルギー流束の式(5.1.2)と比較して\(\cos \theta\)が余計にかかっているのは、面に垂直な方向の運動量流束を表すためです。 恒星内部では輻射は等方的に近く、\(I_\nu (r, \theta) \approx J_\nu (r) \approx B_\nu (T)\)となります。 よって(5.1.6)式は
\[P_\mathrm{rad, \nu} \approx \frac{J_\nu (r)}{c} \int_{4\pi} \cos^2 \theta d\Omega = \frac{4\pi}{3} \frac{J_\nu}{c} \approx \frac{4\pi}{c} \frac{B_\nu (T)}{c} \tag{5.1.7}\]のように近似できます。 輻射圧\(P_\mathrm{rad}\)は\(P_\mathrm{rad, \nu}\)を振動数について積分したものなので、この近似のもとでは
\[P_\mathrm{rad} \approx \frac{4\pi}{3c} \int_0^\infty B_\nu (T) d\nu = \frac{1}{3} a T^4 \tag{5.1.8}\]となります。 ここで\(a\)は放射定数(radiation constant)を表します。 この式は、恒星大気のように\(I_nu(r, \theta)\)の非等方性が大きい場合には使えないことに注意しましょう。
輻射輸送の式 (radiative transfer equation)
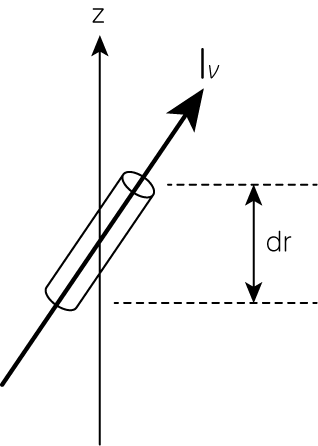
輻射強度\(I_\nu (r, \theta)\)の場所による変化は、輻射輸送の式
\[\cos \theta \frac{dI_\nu}{dr} = - (\kappa_\nu + \sigma_\nu) \rho I_\nu + \eta_\nu \rho + \rho \sigma_\nu J_\nu \tag{5.1.9}\]により記述されます。 ここで\(\kappa_\nu, \sigma_\nu\)はそれぞれ、振動数\(\nu\)の光に対する単位質量あたりのガスの吸収係数と散乱係数です。 これらの量の次元は、単位質量あたりの面積(断面積, cross section)となっていることが(5.1.9)式からわかります。 また\(\eta_\nu\)は、単位立体角・単位振動数間隔あたりのガスの発光係数です。 この式は、光路距離\(dr / \cos \theta\)の間に起こる光の強度変化\(dI_\nu\)を与えます。
右辺の第一項は、吸収と散乱により\(\theta\)方向の輻射強度が減少する効果を表しています。 第二項は、ガスの発行による輻射強度の増加を表します。 また第三項は、他方向の輻射が散乱され\((\theta, \varphi)\)方向に入ってくる光により、その方向の輻射強度が増加する効果を表しています。 ここでは、方向依存性のない(球対称な)散乱を仮定しています。
キルヒホッフの法則 (Kirchhoff’s law)
(局所)熱平衡の場合には、ガスの発光係数\(\eta_\nu\)と\(\kappa_\nu\)との間に、キルヒホッフの法則
\[\eta_\nu = \kappa_\nu B_\nu (T) \tag{5.1.10}\]が成り立ちます。 この関係は、次のように理解できます。 熱平衡状態では光の強度は等方的で、\(I_\nu (\theta) = J_\nu = B_\nu\)となっています。 また平衡状態においては、時間依存性は存在しません。 よってガスにより吸収されるエネルギー\(\kappa_\nu I_\nu (=\kappa_\nu B_\nu)\)と同じエネルギーが放出されなければならず、このことからキルヒホッフの法則が導かれます。
輻射流束 (radiative flux)
(5.1.9)式に\(\cos \theta\)をかけ、全立体角で積分しましょう。
\[\frac{d}{dr} \int_{4\pi} I_\nu (r, \theta) \cos^2 \theta d\Omega = - (\kappa_\nu + \sigma_\nu) \rho F_\nu \tag{5.1.11}\]ここで
\[F_\nu \equiv \int_{4\pi} I_\nu \cos \theta d\Omega\]です。 ここで\(\eta_\nu\)を含む項が消えたのは、ガスの発光には方向依存性が存在せず、\(\cos \theta\)を全立体角で積分することでゼロになるためです。 \(J_\nu\)の項は、\(J_\nu\)が方向に対して平均化された量であることから、同様にゼロになります。 これら2つの項は、ある方向に加わる光とその反対方向に加わる光が全く同じであるため、ある方向のエネルギーの流れには寄与しないとも理解できます。
次に(5.1.11)式の左辺の積分を、近似を用いて評価してみましょう。 恒星内部では輻射場の方向依存性が弱いため
のように書けます。 この関係を(5.1.11)式に代入すると
\[F_\nu = - \frac{4\pi}{3 (\kappa_\nu + \sigma_\nu) \rho} \frac{dB_\nu}{dr} = - \frac{4\pi}{3 (\kappa_\nu + \sigma_\nu) \rho} \frac{dT}{dr} \frac{dB_\nu}{dT} \tag{5.1.13}\]が得られます。 恒星の内部構造に重要なのは、全振動数領域の輻射によるエネルギー流束
\[\frac{L_{r, \mathrm{rad}}}{4\pi r^2} = F_\mathrm{rad} = \int_0^\infty F_\nu d\nu = - \frac{4\pi}{3\rho} \frac{dT}{dr} \int_0^\infty \frac{1}{\kappa_\nu + \sigma_\nu} \frac{dB_\nu}{dT} d\nu \tag{5.1.14}\]です。 ここで\(L_{r, \mathrm{rad}}\)は、恒星中心を中心とする半径\(r\)の球面を、単位時間あたりに外向きに通過する輻射エネルギーを表します。 吸収係数\(\kappa_\nu\)はガス密度と温度と光の振動数の関数であり、振動数に関して非常に複雑な振る舞いを示すことが知られています。 次のように定義されるロスランド平均不透明度 (Rosseland mean opacity)
\[\frac{1}{\kappa} = \frac{\int_0^\infty \frac{1}{\kappa_\nu + \sigma_\nu} \frac{dB_\nu}{dT} d\nu}{\int_0^\infty \frac{dB_\nu}{dT} d\nu} \tag{5.1.15}\]を導入しましょう。 すると(5.1.14)式は
\[\frac{L_{r, \mathrm{rad}}}{4\pi r^2} = - \frac{4\pi}{3\rho \kappa} \frac{dT}{dr} \int_0^\infty \frac{dB_\nu}{dT} d\nu = - \frac{4ac}{3\rho \kappa} T^3 \frac{dT}{dr} \tag{5.1.16}\]のように書き直せます。 この式は、(5.1.8)式で表される輻射圧を用いて
\[\frac{L_{r, \mathrm{rad}}}{4\pi r^2} = - \frac{c}{\rho \kappa} \frac{dP_\mathrm{rad}}{dr} \tag{5.1.17}\]とも表現できます。
エディントン光度 (Eddington luminosity)
静水圧平衡の式に現れる圧力をガス圧と輻射圧に分け、後者に対して(5.1.17)式の関係を用いてみましょう。
\[\begin{align} &- \rho \frac{GM_r}{r^2} = \frac{dP_\mathrm{gas}}{dr} + \frac{dP_\mathrm{rad}}{dr} = \frac{dP_\mathrm{gas}}{dr} - \frac{\kappa \rho L_{r, \mathrm{rad}}}{4\pi c r^2} \notag \\ &\Longrightarrow \ \frac{dP_\mathrm{gas}}{dr} = - \frac{GM_r}{r^2} \rho \left( 1 - \frac{\kappa L_{r, \mathrm{rad}}}{4\pi c G M_r}\right) \tag{5.1.18} \end{align}\]の関係が得られます。 恒星の表面 (\(L_{r, \mathrm{rad}} = L, M_r = M\))に向かって、ガスの密度は減少しているため、ガスの圧力も外側に向かって減少していると考えることができます。 すなわち\(\frac{dP_\mathrm{gas}}{dr} < 0\)であるべきなので、(5.1.18)式から
\[1 - \frac{\kappa L_{r, \mathrm{rad}}}{4\pi c G M_r} > 0 \tag{5.1.19}\]という条件が得られます。 実は、表面に近く密度が非常に薄い場所でのロスランド平均不透明度は、電子散乱による不透明度\(\kappa_\mathrm{el}\)が支配的となります。 さらに水素ヘリウムが完全に電離している状況では、\(\kappa_\mathrm{el} = 0.20 (1+X)\)のように書けます。 よって(5.1.19)式は、恒星の光度\(L\)に対する上限値を与える式
\[L < \frac{4\pi c GM}{\kappa_\mathrm{el}} \equiv L_\mathrm{edd} \simeq 6.5 \times 10^4 \frac{M / M_\odot}{1+X} L_\odot \tag{5.1.20}\]となります。 すなわち、恒星の光度は限界光度\(L_\mathrm{edd}\)よりも小さくなければなりません。 この\(L_\mathrm{edd}\)はエディントン光度とも呼ばれます。
補遺1: 恒星中の温度勾配を見積もってみよう
恒星中の温度勾配は、以下のように概算できます。
\[\left\vert \frac{dT}{dr} \right\vert \approx \frac{T_c}{R} \sim \frac{10^7 \ [\mathrm{K}]}{10^{11} \ [\mathrm{cm}]} \sim 10^{-4} \ [\mathrm{K/cm}]\]一方、光子の平均自由行程は
\[\ell \kappa \rho \sim 1 \ \Longrightarrow \ \ell \sim 0.1 \ [\mathrm{cm}]\]と見積もられます。 この2つの値から、上向きに走る光子と下向きに走る光子の温度差は
\[\ell \left\vert \frac{dT}{dr} \right\vert \sim 10^{-5} \ [\mathrm{K}] \ll 1\]とわかります。 よって、このわずかな温度差(エネルギー差)によって、恒星内部での放射によるエネルギー輸送が起こっていることがわかります。
補遺2: 輻射輸送の式(5.1.9)について
本来、この式は
\[\frac{dI_\nu}{ds} = \frac{\partial r}{\partial s} \frac{\partial I_\nu}{\partial r} + \frac{\partial \theta}{\partial s} \frac{\partial I_\nu}{\partial \theta} = \cos \theta \frac{\partial I_\nu}{\partial r} - \frac{\sin \theta}{r} \frac{\partial I_\nu}{\partial \theta}\]のように書かれます。 しかし恒星内部では\(\left\vert \frac{\partial I_\nu}{\partial r} \right\vert \gg \left\vert \frac{1}{r} \frac{\partial I_\nu}{\partial \theta} \right\vert\)であるため、第二項は無視することができます。
補遺3: エディントン光度の他の導出
(5.1.20)式で出てきたエディント光度は、次のようにも導くことができます。 簡単のため、ガスは完全電離水素のみから成り立っているとしましょう。 そして恒星の質量と光度をそれぞれ\(M, L\)とします。 1つの水素原子と電子に働く重力の大きさの総和は、\(\frac{GM (m_p + m_e)}{r^2}\)です。 そしてこの水素原子が放射から受ける、単位時間あたりの運動量は、電子が受け取るエネルギー\(\frac{\sigma_T}{4\pi r^2} L\)を\(c\)で割ったものに等しくなります。 ここで\(\sigma_T\)は電子のトムソン散乱断面積です。 これらが釣り合う条件を求めると
\[\frac{GM m_p + m_e}{r^2} \simeq \frac{\sigma_T}{4\pi c r^2} L \ \Longrightarrow \ L = \frac{4\pi c G M m_p}{\sigma_T}\]のようになります。 \(\sigma_T / m_p\)を\(\kappa_\mathrm{el}\)に置き換えれば、(5.1.20)式を得ます。
参考文献
[1] 高原文郎, “宇宙物理学”
[2] 野本憲一, 定金晃三, 佐藤勝彦, “恒星”