Table of contents
ブラックホールシャドウ
ISCOの部分で考えたものを質量0の粒子(光子)で考えましょう。
シュバルツシルト計量
シュバルツシルト計量は以下のように与えられます。
\[ds^2 = -(1-\frac{2GM}{c^2 r}) c^2 dt^2 + (1-\frac{2GM}{c^2 r})^{-1} dr^2 + r^2 d\theta^2 + r^2 \sin^2 \theta d \varphi^2\]シュバルツシルト半径を\(r_g = 2GM/c^2\)と定義すると
\[g_{tt} = -(1-\frac{r_g}{r}), \ g_{rr} = \frac{1}{1-\frac{r_g}{r}}, \ g_{\theta \theta} = r^2, \ g_{\varphi \varphi} = r^2 \sin^2 \theta\]質量のない粒子の運動方程式
アフィンパラメータを用いて
\[p^\mu = \frac{dx^\mu}{d\lambda}\]で書かれる4元運動量は
\[\frac{dp_\nu}{dx^0} = \frac{1}{2p^t} p^\mu p^\beta g_{\mu \beta, \nu}\]を満たします。
\(g_{\beta \mu}\)の依存性から\(g_{\beta \mu, t} = 0, g_{\beta \mu, \varphi} = 0\)がわかるので
式変形
光子の4元運動量の内積より
\[0 = g_{tt} p^t p^t + g_{rr} p^r p^r + g_{\theta \theta} p^\theta p^\theta + g_{\varphi \varphi} p^\varphi p^\varphi\]そして
\[p^t = g^{tt} p_t = \frac{1}{1-\frac{r_g}{r}} \frac{\epsilon}{c}\] \[p^\varphi = g^{\varphi \varphi} p_\varphi = \frac{\ell}{r^2 \sin^2 \theta}\]です。球対称の仮定より角運動量が保存し、粒子の運動は一平面に限定できます。簡単のため、\(\theta=\pi/2\)の平面上での運動を考え、\(d\theta = 0\)としましょう。すると上の方程式から
\[0 = -\frac{1}{1-\frac{r_g}{r}} \frac{\epsilon^2}{c^2} + \frac{1}{1-\frac{r_g}{r}} \left( \frac{dr}{d\lambda} \right)^2 + \frac{\ell^2}{r^2} \ \Longrightarrow \ \left( \frac{dr}{d\lambda}\right)^2 = \frac{\epsilon^2}{c^2} - (1-\frac{r_g}{r}) \frac{\ell^2}{r^2}\]となります。
有効ポテンシャルと光子球の半径
有効ポテンシャルを
\[\Psi_{\rm eff} = (1-\frac{r_g}{r}) \frac{\ell^2}{r^2}\]とおくと
\[\frac{d \Psi_{\rm eff}}{dr} = -2\frac{\ell^2}{r^3} + 3\frac{\ell^2 r_g}{r^4} = 0\]となるのは、角運動量の値によらずに
\[r = \frac{3}{2} r_g\]となることがわかります。他に極値を持たず、この点で有効ポテンシャルが最大となります。
ポテンシャルの最大値とブラックホールシャドウ半径
\(r = 3 r_g /2\)のときの有効ポテンシャルの値は
\[\Psi_{\rm eff, max} = \frac{4}{27} \frac{c^2 \ell^2}{r_g^2}\]これよりギリギリのところでブラックホールに落ちる光子のエネルギーは
\[\epsilon > \frac{2}{3\sqrt{3}} \frac{\ell c}{r_g}\]となります。以下の図のように考えると\(p= \epsilon/c, \ell = b p\)と考えることができるので、衝突パラメータ\(b\)が
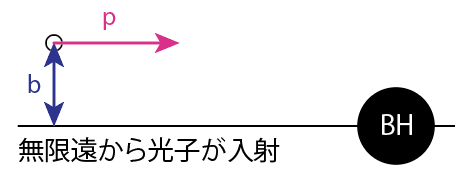
のとき、ブラックホールに光子は落下することになります。これがブラックホールシャドウの半径です。