Table of contents
ラグランジュ微分とオイラー微分
Euler微分の記述法では、場所と時刻を別々の変数としてとらえます。 つまり観測者は動き回る流体要素ではなく、外から眺めているようなイメージです。 一方、Lagrange微分はある時刻における流体要素の場所を変数とします。 こちらは流体要素自身が観測者、ということになります。
Euler的記述法
Euler的記述法では場所\({\bf x}\)と時刻\(t\)とを独立変数として、物理量を\(Q({\bf x}, t)\)のように表します。
Lagrange的記述法
これに対してLagrange的記述法は、適当な時刻\(t=0\)においてある流体要素の位置を\({\bf X}\)と表すとき、任意の時刻\(t\)における同じ流体要素の位置\({\bf x}\)と\({\bf X}\)が
\[{\bf x} = {\bf x} ({\bf X}, t), \ {\bf X} = {\bf X} ({\bf x}, t)\]で関係づけられるとして、一つの流体要素の運動を時間とともに追いかける記述法です。 この関係式は、時刻\(t=0\)に\({\bf X}\)にいた流体要素は時刻\(t\)には必ず\({\bf x}\)の位置にやってくる、ということを意味する式です。このとき
\[{\bf X} = {\bf x}({\bf X}, 0)\]です。
数学的導出
これらより、物理量\(Q\)は
\[Q(\mathbf{x}, t)=Q(\mathbf{x}(\mathbf{X}, t), t)=\tilde{Q}(\mathbf{X}, t), \mathbf{v}(\mathbf{x}, t)=\mathbf{v}(\mathbf{x}(\mathbf{X}, t), t)=\tilde{\mathbf{v}}(\mathbf{X}, t)\]のように書くことができます。ここで\(\tilde{}\)を着けているのは\({\bf x}\)を変数としたときと\({\bf X}\)を変数としたときでは、関数の形が違うことを強調するためです。
それではオイラー的な時間微分\(\partial/\partial t\)とラグランジュ的な時間微分\(D / Dt\)との違いについて考えていきましょう。オイラー的表記では\({\bf x}\)と\(t\)は独立変数なので
です。一方、この\({\bf x}\)のラグランジュ的な時間微分を考えると
\[\frac{D \mathbf{x}}{D t}=\frac{D}{D t} \mathbf{x}(\mathbf{X}, t)=\tilde{\mathbf{v}}(\mathbf{X}, t)=\mathbf{v}(\mathbf{x}, t)\]となり、これは純粋に流体要素の位置の時間変化率、すなわち流体要素の速度を計算していることに一致します。一般的な物理量\(Q({\bf x}, t)\)をラグランジュ微分してみましょう。すると
\[\frac{D}{D t} Q(\mathbf{x}, t)=\frac{\partial}{\partial t} Q(\mathbf{x}, t)+\frac{D \mathbf{x}}{D t} \cdot \frac{\partial}{\partial \mathbf{x}} Q(\mathbf{x}, t)=\left(\frac{\partial}{\partial t}+\mathbf{v} \cdot \nabla\right) Q(\mathbf{x}, t) \Longrightarrow \therefore \frac{D}{D t}=\frac{\partial}{\partial t}+\mathbf{v} \cdot \nabla\]となり、オイラー微分とラグランジュ微分の関係式を導くことができます。
直感的導出
あるマラソンランナーの集団が、冷涼な気候の都市から温暖な気候の都市まで走り抜くという過酷なマラソンに挑戦しているとしましょう。 スタート時刻は早朝の一番気温が低いときで、昼頃の一番暑い時間帯にゴールに到達するというスピード展開でマラソンが行われたとします。
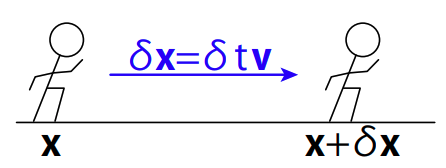
速度\({\bf v}\)で移動するマラソンランナー。
微小時間\(\delta t\)の間に、マラソンランナーが感じる気温の変化には2種類あります。
\[\begin{equation} \delta T_{\text {runner}}=\delta T_{t \rightarrow t+\delta t}+\delta T_{\mathbf{x} \rightarrow \mathbf{x}+\delta \mathbf{x}} \tag{1} \end{equation}\]右辺の第一項は、早朝から走り出してだんだんと時間が経過するにつれて日が高くなり、気温が上昇してくることからランナーが感じる気温の変化を表す項です。第二項は、ランナーが\(\delta t\)の間に\(\delta {\bf x}\)だけ温暖な気候の都市に移動することによって感じる気温の変化です。ランナーの速度を\({\bf v}\)とすると、第二項は温度勾配を用いて
\[\delta T_{\mathbf{x} \rightarrow \mathbf{x}+\delta \mathbf{x}}=\delta t \mathbf{v} \cdot \frac{\delta T}{\delta \mathbf{x}}\]これより(1)の両辺を\(\delta t\)で割ると
\[\frac{\delta T_{\text {runner }}}{\delta t}=\frac{\delta T}{\delta t}+\mathbf{v} \cdot \frac{\delta T}{\delta \mathbf{x}} \stackrel{\delta t \rightarrow 0}{\longrightarrow} \frac{D T}{D t}=\frac{\partial T}{\partial t}+(\mathbf{v} \cdot \nabla) T\]となります。左辺をラグランジュ微分にしたのは、マラソンランナー=気温の測定者、としたためです。
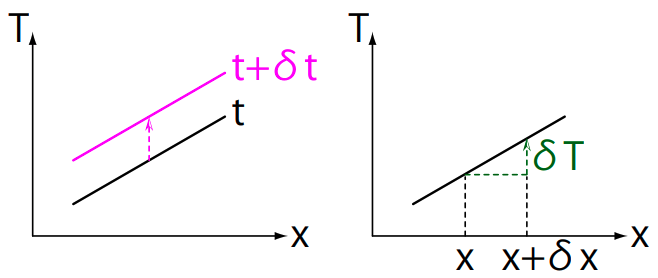
左図: \(\delta t\)経過することによって勝手に気温が変化する。右図: \(\delta t\)の間にランナーが移動することによって気温の変化を感じる。
参考文献
[1] 今井功, “流体力学”
[2] 今井功, “流体力学(前編)”
[3] 境田太樹, “流体力学: 「流れ」を方程式で表すとは”