Table of contents
拡張ラグランジュ関数法
ペナルティ関数法では、ペナルティ関数の重みを表すパラメータ\(\lambda_i\)の値が増加しすぎると、変形して得られた制約なし問題を解くことが数値的に困難になります。
拡張ラグランジュ法(augmented Lagrangian method)では、ラグランジュ関数とペナルティ関数を足し合わせた拡張ラグランジュ関数を用いて、制約つき最適化問題を制約なし最適化問題に変形します。これにより、上述の問題を克服できます。
拡張ラグランジュ関数
ラグランジュ関数\(L(\mathbf{x}, \boldsymbol{\lambda}) = \mathrm{obj}(\mathbf{x}) + \sum_i \lambda_i g_i (\mathbf{x})\)に、等式制約\(g_i(\mathbf{x})=0\)に対するペナルティ関数\(g_i(\mathbf{x})^2\)を足し合わせた
\[L_\rho(\mathbf{x}, \boldsymbol{\lambda}) = \mathrm{obj}(\mathbf{x}) + \sum_{i=0}^{N-1} \lambda_i g_i (\mathbf{x}) + \frac{\rho}{2} \sum_{i=0}^{N-1} g_i (\mathbf{x})^2 \tag{1}\]を\(\mathbf{x}\)について最小化する制約なし最適化問題を解きます。ここで\(\rho>0\)はペナルティ関数の重みを表すパラメータです。
アルゴリズム
拡張ラグランジュ関数を用いて未定乗数更新を行う方法を以下にまとめます。
step 1: パラメータ初期値\(\lambda_i^0, \rho^0\)を設定します。
step 2: (量子)アニーリングにより\(L_{\rho^k} (\mathbf{x}, \boldsymbol{\lambda}^k)\)を最小化するような\(\mathbf{x}\)を求めます。これを\(\mathbf{x}^{\ast (k)}\)と置きます。
step 3: \(\rho^k g(\mathbf{x}^{\ast (k)})\)が0ならば終了します。
step 4: \(\lambda_i^{k+1} = \lambda_i^k + \rho^k g_i (\mathbf{x}^{\ast (k)}), \rho^{k+1} > \rho^k\)を満たすパラメータの値を決定します。\(k \leftarrow k+1\)としてstep 2に戻ります。
拡張ラグランジュ関数法が適用できない例
拡張ラグランジュ関数法はQUBO制約が線形な形をしている場合にしか使えません。例えばグラフ彩色問題を考えましょう。この問題には「隣り合う頂点の色が同じ色になってはならない」という制約があります。この制約をバイナリ変数を使って表現すると以下のようになります。
\[g(\mathbf{x}) = \sum_{(uv) \in E} \sum_{i=0}^{n-1} x_{u, i} x_{v, i}\]ここで\(x_{u, i}\)は頂点\(u\)を色\(i\)で塗るとき1, そうでないとき0となるような変数です。さらに\(n\)はグラフ頂点の総数、\(E\)はグラフに存在する頂点の集合です。
この制約から\(g(\mathbf{x})^2\)を計算すると、これは\(x_{u, i}\)の4次式となります。QUBOはその名前の通り、Quadratic Unconstrained Binary Optimization (制約なし2次形式2値変数最適化)であるため、この制約式を拡張ラグランジュ関数法には適用できません。
TSPによる検証
GitHubにスクリプトをアップロードしています。
github-nakasho/augmented_lagrangian_method
TSPの復習
TSP(巡回セールスマン問題)の目的関数は以下のような数理モデルで定式化されます。
\[\min \quad \sum_t \sum_{i, j} d_{ij} x_{t, i} x_{t+1, j} \quad (0\leq t, i, j \leq N-1)\]\(x_{t, i}\)は\(t\)番目に\(i\)の都市を訪れるとき1, そうでないとき0となるようなバイナリ変数です。\(d_{ij}\)は都市\(i\)と都市\(j\)との距離です。\(N\)は訪れる必要がある都市の総数です。この式は\(t\)番目に訪れる都市\(i\)、その次の\(t+1\)番目に訪れる都市\(j\)との距離を計算し、それを全ての時刻で足し合わせたときに最小になるような組み合わせを求めなさいという問題を表現しています。ただし\(x_{N, i} = x_{0, i}\)として、最後の時刻には最初に出発した都市に戻ってくるものとします。
都市を訪れるにあたり、制約が存在します。1つ目は各時刻において、訪れることができる都市の数は1つに限定されることです。
2つ目は、各都市は1回だけしか訪れることができないことです。
\[\sum_t x_{t, i} = 1 \quad (\forall i) \tag{TSP2}\]従来のQUBO
これまで考えられてきたQUBO化は以下のようなものでした。
\[H = \sum_t \sum_{i, j} d_{ij}x_{t, i} x_{t+1, j} + \lambda_1 \sum_t \left(\sum_i x_{t, i} -1\right)^2 + \lambda_2 \sum_i \left( \sum_t x_{t, i}-1\right)^2 \tag{2}\]右辺の第1項は目的関数、第2項は(TSP1)式の制約、そして第3項は(TSP2)式の制約を表したものです。もし\(\sum_i x_{t, i} \neq 1\)ならば、第2項が正の値を持ちます。
拡張ラグランジュ関数法に合わせたQUBO
(1)式に合わせてQUBOを考えましょう。(TSP1), (TSP2)は以下のような等式制約と考えます。
\[\begin{align} L_\rho (\mathbf{x}, \boldsymbol{\lambda}) &= \sum_t \sum_{i, j} d_{ij}x_{t, i} x_{t+1, j} + \sum_t \lambda_t \left(\sum_i x_{t, i} -1\right) + \sum_i \lambda_i \left( \sum_t x_{t, i} -1\right) \notag \\ &\quad + \frac{\rho}{2} \left\{ \sum_t\left(\sum_i x_{t,i}-1 \right)^2 + \sum_i\left(\sum_t x_{t,i}-1 \right)^2 \right\} \tag{3} \end{align}\]もし\(g_i (\mathbf{x}) = (\sum_t x_{t, i} -1 )^2\)のようにしてしまうと、\(g_i(\mathbf{x})^2\)から、\(L_\rho(\mathbf{x}, \boldsymbol{\lambda})\)が\(x_{t, i}\)の4次式となります。
(2)式では1つの制約に対して1つの制約項を考えました。(3)式ではその式の形から、1つの制約に対して\(N\)個の制約を考えます。もし\(\lambda_1 \sum_t (\sum_i x_{t, i}-1)\)のようにしてしまうと、例えば\(\sum_i x_{t, i} = 2, \sum_i x_{t+1, i} = 0\)のようなものも許されることになり、注意が必要です。
数値実験結果
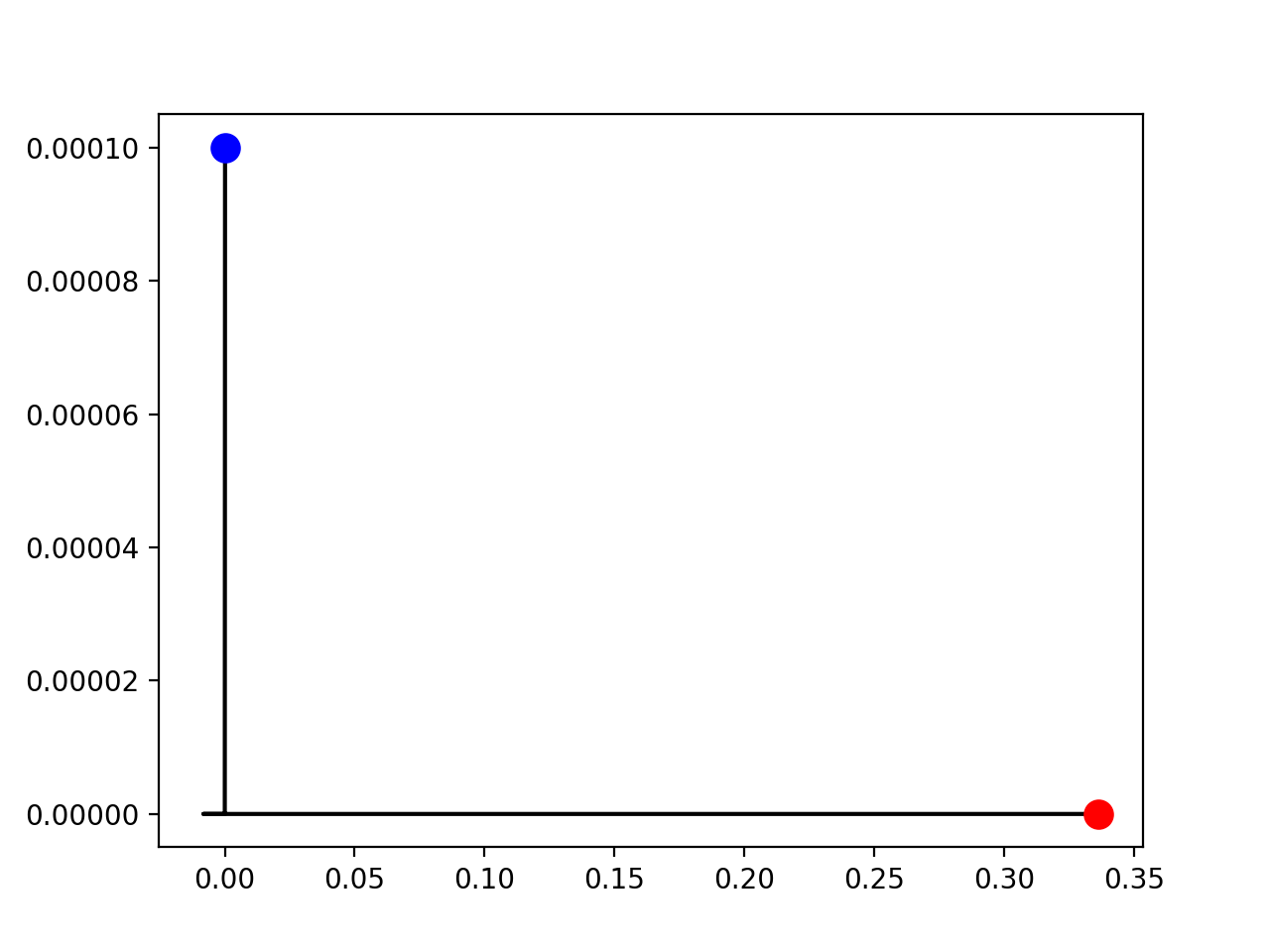
以下に示すのは20都市のTSPを解いたときに現れる、\(\sum_t x_{t, 2} = 1\)の未定乗数と\(\sum_i x_{2, i}=1\)の未定乗数空間の移動の様子です。青がスタート地点(未定乗数の初期値)、赤がゴール地点(最適解が求まったときの未定乗数の値)を表しています。
補題: 未定乗数更新についての証明
\((\mathbf{x}^\ast, \boldsymbol{\lambda}^\ast)\)を等式制約つき最適化問題の最適性の2次の十分条件を満たす点としましょう。このとき(1)式の\(\mathbf{x}\)の勾配を考えると
\[\nabla_{\mathbf{x}} L_\rho (\mathbf{x}^\ast, \boldsymbol{\lambda}^\ast) = \nabla \mathrm{obj}(\mathbf{x}^\ast) + \sum_{i=0}^{N-1} \lambda_i^\ast \nabla g_i (\mathbf{x}^\ast) + \rho \sum_{i=0}^{N-1} \underbrace{g_i (\mathbf{x}^\ast)}_{=0} \nabla g_i (\mathbf{x}^\ast) =\nabla_{\mathbf{x}} H (\mathbf{x}^\ast, \boldsymbol{\lambda}^\ast) = \mathbf{0}\]が成り立ちます。途中、\(\mathbf{x}^\ast\)は最適解であることから\(g_i(\mathbf{x}^\ast)=0\)を用いました。したがって、点\(\mathbf{x}^\ast\)は\(\mathbf{x}\)について拡張ラグランジュ関数\(L_\rho(\mathbf{x}, \boldsymbol{\lambda}^\ast)\)を最小化させる制約なし最適化問題の停留点となります。
次に(1)式のヘッセ行列を考えます。
このとき、\((\nabla g_i (\mathbf{x}^\ast))^\top \mathbf{d} = 0\)を満たす任意の微小ベクトル\(\mathbf{d}\)に対して
\[\mathbf{d}^\top \nabla_{\mathbf{x}\mathbf{x}} L_\rho(\mathbf{x}, \boldsymbol{\lambda}) \mathbf{d} = \mathbf{d}^\top \nabla^2 H (\mathbf{x}^\ast, \boldsymbol{\lambda}^\ast) \mathbf{d} \geq 0\]が成り立ちます。それ以外の任意の微小ベクトルについても、パラメータ\(\rho\)を十分大きくとれば\(\mathbf{d}^\top \nabla_{\mathbf{x}\mathbf{x}} L_\rho (\mathbf{x}^\ast, \boldsymbol{\lambda}^\ast) \mathbf{d} \geq 0\)が成り立ちます。
よって点\(\mathbf{x}^\ast\)は\(\mathbf{x}\)について\(L_\rho (\mathbf{x}, \boldsymbol{\lambda}^\ast)\)を最小化する、制約なし最適化問題の最適性の2次の十分条件を満たす局所最適解になっていることがわかります。これから、\(L_\rho (\mathbf{x}, \boldsymbol{\lambda})\)を最小化する最適化問題を解けば、\(H(\mathbf{x}, \boldsymbol{\lambda})\)の局所最適解\(\mathbf{x}^\ast\)の精度の高い近似解を得ることができます。
拡張ラグランジュ関数法では\(\mathbf{x}\)について\(L_\rho (\mathbf{x}, \boldsymbol{\lambda})\)を最小化した後、\(\boldsymbol{\lambda}\)を更新します。そのために、まず\(\mathbf{x}\)について\(L_\rho (\mathbf{x}, \boldsymbol{\lambda}^{(k)})\)を最小化します。この最適化問題の停留点を\(\mathbf{x}^{\ast (k+1)}\)とします。
注意: \(\mathbf{x}^{(0)}, \boldsymbol{\lambda}^{(0)}\)を出発点に\(\mathbf{x}^{(1)}\)を求める操作を行うので、\(\boldsymbol{\lambda}\)の肩と\(\mathbf{x}\)の肩の値が1つズレていることに注意しましょう。
\[\nabla_\mathbf{x} L_\rho (\mathbf{x}^{\ast (k+1)}, \boldsymbol{\lambda}^{(k)}) = \nabla \mathrm{obj}(\mathbf{x}^{\ast (k+1)}) + \sum \lambda_i^{(k)} \nabla g_i (\mathbf{x}^{\ast (k+1)}) + \rho \sum g_i (\mathbf{x}^{\ast (k+1)}) \nabla g_i (\mathbf{x}^{\ast (k+1)}) = \mathbf{0}\]ここで\(\boldsymbol{\lambda}^{(k+1)} = \boldsymbol{\lambda}^{(k)} + \rho \mathbf{g} (\mathbf{x}^{\ast (k+1)})\)と更新を行うと
\[\begin{aligned} \nabla_\mathbf{x} H(\mathbf{x}^{\ast (k+1)}, \boldsymbol{\lambda}^{(k+1)}) &= \nabla \mathrm{obj} (\mathbf{x}^{\ast (k+1)}) + \sum \lambda_i^{(k+1)} \nabla g_i (\mathbf{x}^{\ast (k+1)}) \\ &= \nabla \mathrm{obj} (\mathbf{x}^{\ast (k+1)}) + \sum (\lambda_i^{(k)} + \rho g_i (\mathbf{x}^{\ast (k+1)})) \nabla g_i (\mathbf{x}^{\ast (k+1)}) \\ &= \nabla \mathrm{obj} (\mathbf{x}^{\ast (k+1)}) + \sum \lambda_i^{(k)} \nabla g_i (\mathbf{x}^{\ast (k+1)}) + \rho \sum g_i(\mathbf{x}^{\ast (k+1)}) \nabla g_i (\mathbf{x}^{\ast (k+1)}) \\ &= \nabla_\mathbf{x} L_\rho (\mathbf{x}^{\ast (k+1)}, \boldsymbol{\lambda}^{(k)}) = \mathbf{0} \end{aligned}\]となります。このように、拡張ラグランジュ関数法は等式制約つき最適化問題の最適性の1次の必要条件のうち
\[\nabla_\mathbf{x} H (\mathbf{x}^{\ast (k)}, \boldsymbol{\lambda}^{(k)}) = \nabla \mathrm{obj} (\mathbf{x}^{\ast (k)}) + \sum \lambda_i^{(k)} \nabla g_i (\mathbf{x}^{\ast (k)}) = \mathbf{0}\]を満たしつつ、最終的に
\[\nabla_\boldsymbol{\lambda} H(\mathbf{x}^{\ast (k)}, \boldsymbol{\lambda}^{(k)}) = \mathbf{g} (\mathbf{x}^{\ast (k)}) = \mathbf{0}\]を満たす\((\mathbf{x}^{\ast (k)}, \boldsymbol{\lambda}^{(k)})\)を求める手法です。
参考文献
[1] 梅谷俊治, “しっかり学ぶ数理最適化 モデルからアルゴリズムまで”
[2] 等式制約あり最適化問題と拡張ラグランジュ乗数法
[3] 山下信雄, 数理計画法 第3回目: 最適性の条件1