Table of contents
中性子星の冷却進化
大質量星の超新星爆発により誕生した中性子星は、初期にはその内部温度が\(10^{12} \mathrm{K}\)を超える非常に高温の状態とされています。 しかし、中性子星から新たにニュートリノが放出されることで、その温度は\(10^{10} \mathrm{K}\)まで急激に冷却されます。 このニュートリノ冷却期は、約\(10^5\)年ほど続くとされています。 この後は、中性子星表面からの光子放出が冷却機構として優勢になります。 そのため、中性子星から飛来する放射を検出するすることは、中性子星の内部構造や表面の情報を得るために非常に重要であるとわかります。 しかし、中性子星表面から直接放出される熱的放射を検出することは、中性子星を取り巻く磁気圏環境からくる放射などにより、非常に困難です。 そのため、これまでに表面からの熱的放射を直接観測した例は、わずかしか存在しません。
中性子星の冷却計算は、概念的には極めて簡単に計算することができます。 中性子星内部は電子が強く縮退しているため、熱伝導度がとても高く、ほぼ一様温度になっていると近似できるためです。 強く内部が縮退している中性子星が、\(N\)個のフェルミ粒子から形成されているとしましょう。 そして中性子星の内部温度は\(T\)で一定であるとすると、中性子星の熱容量が
と計算されます。 ここで\(x \equiv p_F / mc\)であり、さらに\(m\)はフェルミ粒子の質量です。 そして中性子星の全熱容量は\(U = T C_V\)のように書けるため、中性子星の冷却進化を支配する方程式が
\[\frac{dU}{dt} = C_V \frac{dT}{dt} = - (L_\nu + L_\gamma) \tag{2}\]のようになります。 ここで\(L_\nu = \int_0^M \epsilon_\nu dV\)は中性子星内部からのニュートリノ光度であり、\(\epsilon_\nu\)は単位体積あたりのニュートリノ生成率です。 そして\(L_\gamma\)は、中性子星表面からの光子光度を表しています。 中性子星が黒体であり、光学的厚みが\(\tau \sim 1\)の領域から黒体放射を出しているとすると、電磁波による光度は
\[L_\gamma = 4\pi R^2 \sigma_\mathrm{SB} T_e^4 = 7 \times 10^{36} \left( \frac{R}{10^6 \mathrm{cm}}\right)^2 \left( \frac{T_e}{10^7 \mathrm{K}}\right)^4 \ [\mathrm{erg/s}] \tag{3}\]と求まります。 ここで、中性子星表面での有効温度を\(T_e\)としましたが、これは必ずしも内部温度\(T\)と一致しません。 詳細なモデル計算から、\(T\)と\(T_e\)の関係が
\[\frac{T_e}{T} \simeq 1 \times 10^{-2} \left( \frac{T_e}{10^9 \mathrm{K}}\right)^{-1/8} \left( \frac{M}{M_\odot}\right)^{1/4} \left( \frac{R}{10^6 \mathrm{cm}}\right)^{-1/2} \tag{4}\]となることが知られています。 ただし、この関係は外層の組成に依存して変化します。
次の図は、観測されている孤立中性子星に対し、横軸を中性子星の年齢、縦軸を表面の中性子星の温度としたものです。
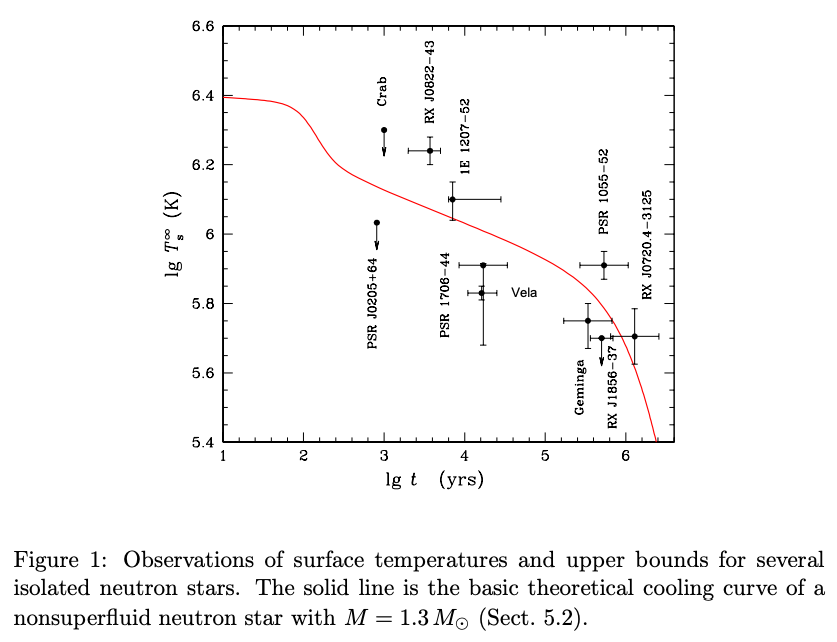
Yakovlev & Pethick (2004)より。赤線は、\(M=1.3M_\odot\)の超流動のない中性子星の冷却曲線を理論から求めたもの。
ニュートリノ生成メカニズム
中性子星の冷却進化を理解するためには、ニュートリノ放射によるエネルギー損失率\(\epsilon_\nu\)を知る必要があります。 生まれたばかりの中性子星内部から生成されるニュートリノは、内部物質と相互作用することなく外部に抜け出し、エネルギーを持ち出します。 ここでは数あるニュートリノ放射メカニズムの中から、いくつかをピックアップして説明します。
(Direct) URCA (DURCA) 反応
これは以下のようなものです。
\[n \longrightarrow p + e^- + \bar{\nu}_e, \quad p + e^- \longrightarrow n + \nu_e \tag{5}\]この反応は、冷たい中性子星のような強く縮退している物質内では効率が悪くなります。 体積\(\mathcal{V}\)中の反ニュートリノによる全光度は、以下のようにして計算することができます。
\[L_{\bar{\nu}}^D = \frac{(2\pi)^4}{\hbar \mathcal{V}} \int d^3 n_n d^3 n_p d^3 n_e d^3 n_\bar{\nu} \delta (E_f - E_i) \delta^3 (\mathbf{k}_f - \mathbf{k}_i) S \vert H_{fi}^2 \vert E_\bar{\nu} \Theta \tag{6}\]ここで\(\mathbf{p}_j = \hbar \mathbf{k}_j\)であり
\[d^3 n_j = \mathcal{V} \frac{d^3 p_j}{h^3} \tag{7}\] \[S = f_n (1-f_p) (1-f_e) \tag{8}\] \[f_j = \frac{1}{\exp [(E_j - \mu_j)/k_B T] + 1} \tag{9}\]です。 さらに\(\vert H_{fi} \vert\)は反応振幅の2乗で、終状態のスピンと初期状態のスピンの平均で総和をとる必要があります。 \(p_F (n), p_F (p), p_F (e)\)の3つのフェルミ運動量が三角条件\(p_F (n) \leq p_F (p) + p_F (e)\)を満たす場合、\(\Theta = 1\)ですが、そうでない場合は\(\Theta = 0\)となります。 この場合の放射率は、以下のように計算されています (例えば、Prakash et al. (1992)などをご覧ください。)
\[\epsilon_\bar{\nu}^\mathrm{DURCA} = \frac{L^D_\bar{\nu}}{\mathcal{V}} \approx 4 \times 10^{27} \left( \frac{n_e}{n_0}\right)^{1/3} \frac{m_n^\ast m_p^\ast}{m_n^2} T_9^6 \Theta \ [\mathrm{erg/s/cm^3}] \tag{10}\]ここで\(T_9 = T / 10^9 \mathrm{K}, n_0 = 0.16 \mathrm{fm}^{-3}\)であり、\(m_j^\ast\)は有効粒子質量です。 \(\epsilon_\bar{\nu}\)の温度依存性は全て、位相空間のファクターとして現れています。
Modified URCA (MURCA) 反応 (Chiu & Salpeter (1964))
DURCAでは、中性子・陽子・電子の運動量が三角条件を満たし場合のみを計算していました。 そのため、中性子星の中でも高密度かつ強く縮退している場合にのみ適応できる計算です。 そこで、以下のような修正されたURCA過程 (MURCA)を考えてみましょう。
\[n + n \longrightarrow n + p + e^- + \bar{\nu}_e, \quad n + p + e^- \longrightarrow n + n + \nu_e \tag{11}\] \[n + n \longrightarrow n + p + \mu^- + \bar{\nu}_\mu, \quad n + p + \mu^- \longrightarrow n + n + \nu_\mu \tag{12}\]この場合の反ニュートリノによる全光度は
\[L_\bar{\nu}^M = \frac{(2\pi)^4}{\hbar \mathcal{V}} \int d^3 n_1 d^3 n_2 d^3 n_{1'} d^3 n_p d^3 n_e d^3 n_\bar{\nu} \delta (E_f - E_i) \delta^3 (\mathbf{k}_f - \mathbf{k}_i) S \vert H_{fi}^2 \vert E_\bar{\nu} \tag{13}\]のようになります。 添字の\(1, 2, 1'\)は、初期の2つの中性子と、終状態の1つの中性子を表します。 そして
\[S = f_1 f_2 (1-f_{1'}) (1-f_p) (1-f_e) \tag{14}\]です。 そしてこの場合のニュートリノ放射率は
\[\epsilon_\bar{\nu}^\mathrm{MURCA} \equiv \frac{L_\bar{\nu}^M}{\mathcal{V}} \simeq 7.4 \times 10^{20} \left( \frac{\rho}{\rho_\mathrm{nuc}}\right)^{2/3} T_9^8 (1+F) \ [\mathrm{erg/s/cm^3}] \tag{15}\]のように求まります。 ここで\(\rho_\mathrm{nuc} = 2.8 \times 10^{14} \mathrm{g/cm^3}, T_9 = T/ 10^9 \mathrm{K}\)です。 さらに\(\mu_e > m_\mu c^2 \ (\rho > 2.9 \rho_\mathrm{nuc})\)の場合\(F= \frac{p_\mu^2 dp_\mu}{p_e^2 dp_e}\)、そうでない場合は\(F=0\)となります。 中性子星が質量\(M\)の一様密度の星の場合、Friman & Maxwell (1979)から
\[L_\bar{\nu}^\mathrm{MURCA} \simeq 5.3 \times 10^{39} \frac{M}{M_\odot} \left( \frac{\rho_\mathrm{nuc}}{\rho}\right)^{1/3} T_9^8 \ [\mathrm{erg/s}] \tag{16}\]のように計算がされています。
原子核ペアの制動放射 (Flowers et al. (1975), Friman & Maxwell (1979))
中性子と中性子/陽子が散乱を起こし、光子の代わりにニュートリノを放出するものです。
\[n + n \longrightarrow n + n + \nu + \bar{\nu} \tag{17}\] \[n + p \longrightarrow n + p + \nu + \bar{\nu} \tag{18}\]この過程はMURCA過程と比較して、非効率であることが知られています。
ニュートリノペア制動放射
電子と原子核が散乱を起こし、ニュートリノを放出します。
\[e^- + (Z, A) \longrightarrow e^- + (Z, A) + \nu + \bar{\nu} \tag{19}\]この反応による光度は
\[L_\nu^\mathrm{brem} \simeq 5 \times 10^{39} \frac{M_\mathrm{crust}}{M_\odot} T_9^6 \ [\mathrm{erg/s}] \tag{20}\]のよう求まっています。 ここで\(M_\mathrm{crust}\)は、中性子星の固体クラストの質量です。
\(\pi\)中間子凝縮における\(\pi\)中間子の反応
これは\(\pi\)中間子において、核子準粒子の\(\beta\)崩壊および逆\(\beta\)崩壊により、ニュートリノが発生するというものです。
\[\pi^- + n \longrightarrow n + e^- + \bar{\nu}_e, \quad n + e^- \longrightarrow n + \pi^- + \nu_e \tag{21}\] \[\pi^- + n \longrightarrow n + \mu^- + \bar{\nu}_\mu, \quad n + \mu^- \longrightarrow n + \pi^- + \nu_\mu \tag{22}\]これによる光度は
\[L_\nu^\pi \simeq 1.5 \times 10^{46} \theta^2 \frac{M}{M_\odot} \frac{\rho_\mathrm{nuc}}{\rho} T_9^6 \ [\mathrm{erg/s}] \tag{23}\]のように求まっています。 ここで\(\theta \sim 0.3\)は、\(\pi\)中間子のdegree (度数?)の角度測定です。 \(\pi\)中間子凝縮が起こると、この冷却機構はMURCA過程よりも効率よく起こることが知られています。
クォークの\(\beta\)崩壊 (Iwamoto (1980))
\[d \longrightarrow u + e^- + \bar{\nu}_e, \quad u + e^- \longrightarrow d + \nu_e \tag{24}\]のような反応によるニュートリノ放出です。 このときのエネルギー放出率は
\[\epsilon_\nu^\mathrm{quark} \simeq 1.9 \times 10^{25} \frac{n}{n_\mathrm{nuc}} T_9^6 \ [\mathrm{erg/s/cm^3}] \tag{25}\]と求まっています。 ここで\(n_\mathrm{nuc} = \rho_\mathrm{nuc} / m_B = 0.17 \mathrm{fm^-3}\)です。 一様密度の星と仮定すると、光度は
\[L_\nu^\mathrm{quark} \simeq 1.3 \times 10^{44} \frac{M}{M_\odot} T_9^6 \ [\mathrm{erg/s}] \tag{26}\]クーパー対の形成・崩壊 (Flowers et al. (1976))
超流動体や超伝導体では、単一粒子(クーパー対の崩壊した励起状態)との熱平衡状態にあります。 つまりクーパー対の形成や崩壊が起こっており、それに伴ってニュートリノ対を放出しています。
\[X + X \longrightarrow [XX] + \nu + \bar{\nu} \tag{27}\]\([XX]\)は粒子\(X\)(中性子、陽子、ハイペロン、クォークなど)のクーパー対を表します。 中性子\({}^3 P_2\)のペアによる放射率は
\[\epsilon_\nu^{\hspace{1mm}^3 P_2 (n)} = 8.6 \times 10^{21} \left( \frac{n_n}{n_0}\right)^{1/3} \left( \frac{m_n^\ast}{m_n}\right) R_{\hspace{1mm}^3 P_2 (n)} (T / T_c) T_9^7 \ [\mathrm{erg/s/cm^3}] \tag{28}\]のように求められています。 ここで\(T_c\)は超流動への転移温度、\(m_n^\ast\)は中性子の有効質量、そして\(n_0\)は飽和数密度です。
ニュートリノ放射率についてのレビュー論文がいくつか出版されています。詳細はYakovlev et al. (1999), Yakovlev et al. (2001)などをご覧ください。
単純な冷却計算
\(\rho \simeq \rho_\mathrm{nuc}\)の場合、\(n_n \gg n_p\)となります。 これは中性子星が中性子のみから構成されると近似した場合に相当し、単純な冷却計算が可能になります。 中性子星を構成する中性子が非相対論的な場合、中性子星の熱容量は
\[C_V \simeq N \frac{\pi^2}{2} k_B \frac{k_B T}{E'_F (n)} \tag{29}\]のようになります。 すると中性子星が持つ全熱量は
\[U_n = T C_V \simeq \frac{M}{m_n} \frac{\pi^2}{2} \frac{(k_B T)^2}{E'_F (n)} \simeq 6 \times 10^{47} \frac{M}{M_\odot} \left( \frac{\rho}{\rho_\mathrm{nuc}}\right)^{-2/3} T_9^2 \ [\mathrm{erg}] \tag{30}\]冷却進化の方程式(2)において、\(U = U_n\)とし、さらにニュートリノと光子による光度\(L_\nu, L_\gamma\)を代入します。 さらに\(\rho, M, R\)を定数と仮定すれば、中性子星内部の温度\(T\)の常微分方程式を得ることができます。 以降では単一のエネルギー損失過程のみに着目して、冷却進化方程式(2)を積分し、冷却の時間スケールを求めた結果を見ていきましょう。
MURCA過程
\[\Delta t (\mathrm{MURCA}) \simeq 1 \left( \frac{\rho}{\rho_\mathrm{nuc}}\right)^{-1/3} T_9^{-6} (f) \left\{ 1 - \left( \frac{T_9 (f)}{T_9 (i)}\right)^6\right\} \ [\mathrm{yr}] \tag{31}\]または
\[T_9 (f: \mathrm{MURCA}) \propto \left( \frac{\Delta t}{1 \mathrm{yr}}\right)^{-1/6} \tag{32}\]\(\pi\)中間子凝縮体における\(\pi\)中間子反応
\[\Delta t (\mathrm{pion}) \simeq 20 \theta^2 \left( \frac{\rho}{\rho_\mathrm{nuc}}\right)^{1/3} T_9^{-4} (f) \left\{ 1 - \left( \frac{T_9 (f)}{T_9(i)}\right)^4 \right\} \ [\mathrm{s}]\tag{33}\]または
\[T_9 (f: \mathrm{pion}) \propto \left( \frac{\Delta t}{20 \mathrm{s}}\right)^{-1/4} \tag{34}\]クォークの\(\beta\)崩壊
\[\Delta t (\mathrm{quark}) \simeq 1 \left( \frac{\rho}{\rho_\mathrm{nuc}}\right)^{-1/3} T_9^{-4} (f) \left\{ 1 - \left( \frac{T_9 (f)}{T_9(i)}\right)^4 \right\} \ [\mathrm{hr}]\tag{35}\]または
\[T_9 (f: \mathrm{quark}) \propto \left( \frac{\Delta t}{1 \mathrm{hr}}\right)^{-1/4} \tag{36}\]ニュートリノ対制動放射
\[\Delta t (\mathrm{brem}) \simeq 2 \left( \frac{\rho}{\rho_\mathrm{nuc}}\right)^{-2/3} T_9^{-4} (f) \left\{ 1 - \left( \frac{T_9 (f)}{T_9(i)}\right)^4 \right\} \ [\mathrm{yr}]\tag{37}\]または
\[T_9 (f: \mathrm{brem}) \propto \left( \frac{\Delta t}{2 \mathrm{yr}}\right)^{-1/4} \tag{38}\]表面からの光子放出
最後に、表面からの光子放出による冷却時間を見てみましょう。 電子の有効温度\(T_e\)と内部温度\(T\)の間に、\(T_e \approx 10^{-2} \alpha T \ (0.1 \gtrsim \alpha \gtrsim 1)\)のような関係が成り立っているとして計算すると
\[\Delta t (\mathrm{photon}) \simeq 2 \times 10^3 \alpha^2 \left( \frac{M}{M_\odot}\right)^{1/3} T_{e, 7}^{-2} (f) \left\{ 1 - \left( \frac{T_{e, 7} (f)}{T_{e, 7}(i)}\right)^2 \right\} \ [\mathrm{yr}]\tag{39}\]または
\[T_{e, 7} (f: \mathrm{photon}) \propto \left( \frac{\Delta t}{2 \times 10^3 \mathrm{yr}}\right)^{-1/2} \tag{40}\]となります。 ここで\(T_{e, 7} = T_e / 10^7 \mathrm{K}\)、\(T_i\)と\(T (f)\)はそれぞれ積分の初期温度と最終温度です。 また\(M = 4\pi \rho R^3 / 3\)のような近似を用いて求められています。 これらからわかるように、ニュートリノによる冷却は光子による冷却に比べてとても効率的に起こることがわかります。
超流動性
超流動の顕著な性質として、摩擦が存在しないことが挙げられます。 これはすなわち、流体の運動に伴うエネルギーの散逸がないことを意味します。 超流動現象は、極低温にまで冷やした液体ヘリウム \({}^4 \mathrm{He}\)で発見されました。 ヘリウム粒子はボゾンであるため、超流動はボーズ・アインシュタイン凝縮に関連するものだろうと考えられました。 実際、ボーズ・アインシュタイン凝縮理論により求められた理想ヘリウム液体の臨界温度\(T_c\)が、実験で観測された超流動転移温度\(T_\lambda\)に近かったのです。 もう一つの大きな特徴として、超流動体は\(T_\lambda\)で熱容量が不連続に変化し、\(T_\lambda\)からは温度\(T\)に対して指数的に熱容量が減少します。 これらの特徴は2流体モデルを用いて説明することができます。 普通の流体と超流動体の密度をそれぞれ\(\rho_n, \rho_s\)としましょう。 そして全体の密度を
\[\rho = \rho_n + \rho_s \tag{41}\]とします。 そして\(T \rightarrow 0\)では\(\rho_n \rightarrow 0, \rho_s \rightarrow \rho\)、\(T \rightarrow T_\lambda\)では\(\rho_n \rightarrow \rho, \rho_s \rightarrow 0\)を仮定します。 超流動成分は基底状態にいる粒子、すなわち凝縮粒子から構成され、通常流体成分は励起状態にいる粒子から構成されるとします。 つまり、超流動体における粘性現象は、通常の流体成分が担っていると考えます。
これは理想ボーズ液体のボーズ・アインシュタイン凝縮に見られる状況にとても似ています。 \(T< T_c\)では、粒子は基底状態にいるものと励起状態にいるものとに分かれます。 ボーズ流体での粒子の数密度を\(n\)とすると
のように書くことができます。 ここで\(n_0, n_\mathrm{ex}\)はそれぞれ、基底状態と励起状態にある粒子数密度です。 そして\(T \rightarrow 0\)で\(n_0 \rightarrow n, n_\mathrm{ex} \rightarrow 0\)であり、\(T \rightarrow T_c\)で\(n_0 \rightarrow 0, n_\mathrm{ex} \rightarrow n\)となります。
ボーズ液体の超流動性
流体中の粒子は、お互いに強く相互作用しあい、集団的に運動をします。 そのため、この物理現象のモデル化には、自由粒子の粒子状態とは異なるテクニックが必要となります。 量子力学も考慮して流体を扱おうとすると、粒子の集団運動を取り扱うために、準粒子もしくは素励起を導入する必要が出てきます。 これらはエネルギー\(\epsilon = \hbar \omega\)と線形運動量\(\mathbf{p} = \hbar \mathbf{k}\)を持ちます。 ボーズ液体の準粒子は、ボゾンと同様の振る舞いもします。 この準粒子をフォノン(音子?)と呼び、音速\(u\)と\(p = \vert \mathbf{p} \vert\)を用いて\(\epsilon = up\)のような分散関係を持ちます。 準粒子と基底状態にある流体が同時に存在する場合、ある時刻において次のような条件が満たされなければなりません。
\[v > \frac{\epsilon}{p} \tag{43}\]ここで\(v\)は基底状態にある流体の速度、\(\epsilon, p\)はそれぞれ準粒子のエネルギーと運動量です。 この条件から、\(\epsilon / p\)の最小値が存在する場合、\(v < v_\mathrm{min} = (\epsilon / p)_\mathrm{min}\)となるような基底状態の流体は、準粒子と一緒に存在できないことを示唆しています。 準粒子の生成は基底状態にある流体のエネルギー散逸過程とみなせるため、\(v < v_\mathrm{min}\)の場合には流体が超流動状態で散逸がなく、準粒子が励起できないことを意味しています。
フェルミ液体の超流動性
中性子や陽子といったフェルミオンも、超流動となります。 核子同士が核力で引き合うことで、ボーズ粒子として振る舞うクーパー対を形成します。 フェルミ液体の超流動性は、\({}^3 \mathrm{He}\)液体で発見されました。 この現象は\({}^4 \mathrm{He}\)液体よりもだいぶ小さい転移温度\(T_\lambda\)を持つのが特徴です。 中性子星中の中性子は強く縮退しています。 そのため、運動量空間においてフェルミ面近傍の異なるスピン状態を占有する2つの中性子が、クーパー対を形成します。 クーパー対の角運動量状態は、対を形成する軌道角運動量\(L\)に依存し、通常は\(L=0\)の\(S\)状態か、\(L=1\)の\(P\)状態を占有しています。 固体クラスト中の中性子は、\(S\)状態のクーパー対から構成される超流動を形成している考えられています。 それとは対照的に、中性子星コア中の中性子は、\(P\)状態のペアから構成される超流動を形成していると考えられており、その状態は中性子流体の密度に依存します。 フェルミオン超流動において、クーパー対の大多数は基底状態にあります。 基底状態と第一励起状態とのエネルギーギャップを\(\delta\)と書くことにしましょう。 一般的に、\(\delta\)は温度\(T\)に依存します。 この素励起における分散関係式は、以下のように与えられます。
\[\epsilon (p) = \sqrt{\delta^2 + \xi_p^2} \tag{44}\]ここで\(\epsilon\)はフェルミエネルギー、\(\xi_p \equiv v (p-p_0), v=p/m\)、そして\(p_0\)はフェルミ面での運動量です。 \(\epsilon / (p - p_0)\)は非ゼロとなり、液体の超流動性の存在が示唆されます。
熱容量とニュートリノ放射率に対する超流動性の影響を考慮する場合、通常の流体の物理量を超流動の量に変換する計算が必要となります。 核子の熱容量は
のように与えられます。 ここで\(C_N^\mathrm{normal}\)は通常の核子の熱容量、\(R_C (T/T_c)\)は制御因子と呼ばれ、超流動性による熱容量の変化を表すものです。 ニュートリノ放出率に関しても、同様に書くことができます。
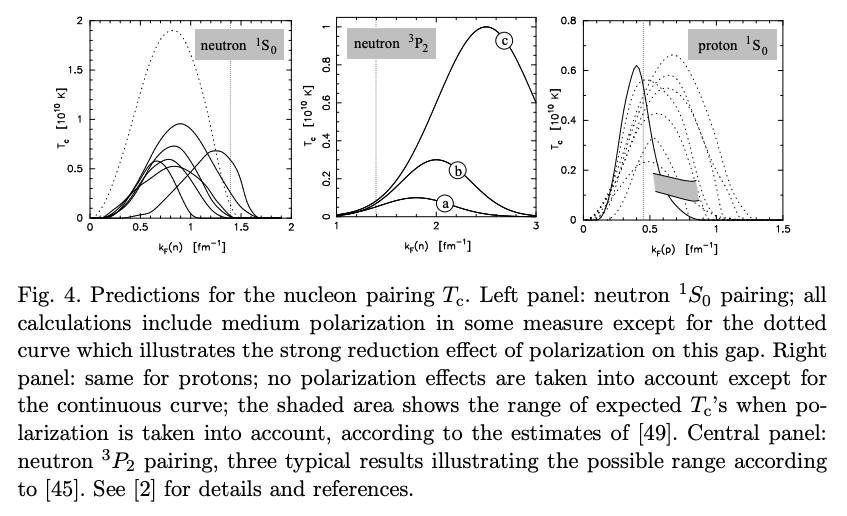
\[\epsilon_\nu^\mathrm{paired} = \epsilon_\nu^\mathrm{normal} \times R_\nu (T / T_c) \tag{46}\]ここで\(\epsilon_\nu^\mathrm{normal}\)は通常の流体における放出率で、\(R_\nu (T / T_c)\)がこの場合の制御因子になります。 これらは\(T>T_c\)で\(R_C = R_\nu = 1\)である必要があります。 次の図は、\({}^1 S_0\)対などを形成する温度を理論予測したグラフです。
さらに次の図は、\(R(T/ T_c), c_V, \epsilon_\nu\)を計算したものです。
恒星進化としての冷却計算
観測と比較するために、理論モデルからわかる中性子星の冷却進化を計算する必要があります。 中性子星は非常に重力が強いため、恒星進化の部分で用いられているニュートン重力を、一般相対論に拡張する必要があります。 一般相対論的な恒星進化の方程式群は、以下のように与えられます (詳しくはThorne (1977)などをご覧ください。)
\[\frac{dP}{dm} = - \frac{Gm}{4\pi r^4} \frac{\rho}{\rho_m} \left( \frac{M_r + 4\pi r^3 P / c^2}{m}\right) \left( 1 + \frac{P}{\rho c^2}\right) \left( 1 - \frac{2GM_r}{rc^2}\right)^{-1/2} \tag{47}\] \[\frac{dr}{dm} = \frac{1}{4\pi r^2 \rho_m} \left( 1 - \frac{2GM_r}{rc^2}\right)^{1/2} \tag{48}\] \[\frac{d\phi}{dm} = \frac{Gm}{4\pi r^4 \rho_m c^2} \left( \frac{M_r + 4\pi r^3 P / c^2}{m}\right) \left( 1 - \frac{2GM_r}{rc^2}\right)^{-1/2} \tag{49}\] \[\frac{dM_r}{dm} = \frac{\rho}{\rho_m} \left( 1 - \frac{2GM_r}{rc^2}\right)^{1/2} \tag{50}\] \[\frac{d (T e^\phi)}{dm} = - \frac{3\kappa L_r e^\phi}{256 \pi^2 \sigma_\mathrm{SB} r^4 T^3} \tag{51}\] \[\frac{d (L_r e^{2\phi})}{dm} = - e^{2\phi} \left\{ \frac{\epsilon_\nu - \epsilon_h}{\rho_m} + T e^{-\phi} \frac{d}{dt} \left( \frac{s}{\rho_m}\right) \right\} \tag{52}\]ここで\(P\)は圧力、\(T\)は温度、\(S\)は単位体積あたりのエントロピーです。 \(\rho_m = m_u n_b\)はバリオン質量密度で、\(n_b\)はバリオン数密度です。 \(\rho \equiv \epsilon / c^2\)はエネルギー密度を表し、\(\phi c^2\)は重力赤方偏移を決定するメトリック関数です。 そして
\[M_r = \int_0^r 4\pi r^2 \rho dr \tag{53}\]は、中性子星中心から半径\(r\)の球面内に含まれる重力質量であり
\[m = \int_0^r 4\pi r^2 \rho_m \left( 1 - \frac{2GM_r}{rc^2}\right)^{-1/2} dr \tag{54}\]は、同様に半径\(r\)内に含まれるバリオン質量です。 \(L_r\)は半径\(r\)における光度ですが、これはニュートリノを含まないものとして定義されます。 \(\epsilon_\nu, \epsilon_h\)はそれぞれ、単位体積あたりのニュートリノ放出率と加熱率です。 そして\(\kappa\)は不透明度を表します。 最後に、\(t\)はシュバルツシルト座標時間での時刻を表し、無限遠での固有時を表します。 \(\rho\)と\(\rho_m\)の間には、\(\rho = \rho_m (1 + u/c^2)\)の関係が成り立ちます。 ここに、\(u\)は(静止エネルギーも含めた)固有内部エネルギーです。 またエントロピーの時間微分は
\[\frac{dS}{dt} = \frac{C_V}{T} \frac{dT}{dt} + \left( \frac{\partial S}{\partial \rho_m}\right)_T \frac{d\rho_m}{dt} \tag{55}\]のように書かれます。 \(C_V\)は単位堆積あたりの定積熱容量です。 またここでは、\(\frac{d\rho_m}{dt}\)の項は通常は無視できるほど小さいことに注意が必要です。
適切な物理的状況を入力として用いることで、上述の方程式群を用いて中性子星の冷却進化を計算することができます。 ここでいう入力とは
- 中性子星の構造を与える状態方程式\(P = P(\rho, T)\)と\(C_V\)
- 輻射と熱伝導の不透明度 \(\kappa\)
- ニュートリノ放射率 \(\epsilon_\nu\)
- 加熱率 \(\epsilon_h\)
- 超流動が起こる遷移温度\(T_c\)
のようなものが考えられます。 そしてこれまで議論してきたように、超流動と超伝導、そして磁場の効果を適切に考慮することで、冷却進化の計算を行うことができます。
光子の光度を\(L_\gamma\)は
のように書かれます。 ここで\(T_e\)は有効温度です。 観測者は、恒星表面の局所的な情報から\(L, R, T_e\)を求めることができます。 無限遠にいる観測者は、\(L_\infty = e^{2\phi} L_\gamma, T_\infty = e^\phi T_e, R_\infty = e^{-\phi} R \ (e^{2\phi} = g_{00})\)のように、重力赤方偏移を受けた量を観測することになります。 ここで\(g_{00}\)は、メトリックの時間成分で、これは赤方偏移\(z\)と\(e^{-\phi} = 1+z\)の関係にあります。 よって
\[L_\infty = 4\pi R_\infty^2 \sigma_\mathrm{SB} T_\infty^4 \tag{57}\]冷却進化計算のアウトプットでメインとなるのは\(L_\gamma\) (または\(L_\infty\))であり、ここから、有効温度\(T_e\) (または\(T_\infty\))を得ることができます。
参考文献
[1] Yakovlev & Pethick, 2004, “Neutron Star Cooling”
[2] Chiu & Salpeter, 1964, “Surface X-Ray Emission from Neutron Stars”
[3] Friman & Maxwell, 1979, “Neutrino emissivities of neutron stars”
[4] Flowers et al., 1975, “Neutrino pair bremsstrahlung by nucleons in neutron star matter”
[5] Iwamoto, 1980, “Quark Beta Decay and the Cooling of Neutron Stars”
[6] Flowers et al., 1976, “Neutrino pair emission from finite-temperature neutron superfluid and the cooling of young neutron stars”
[7] Yakovlev et al., 1999, “Neutrino emission due to Cooper pairing of nucleons in cooling neutron stars”
[8] Yakovlev et al., 2001, “Neutrino emission from neutron stars”
[9] Page et al., 2006, “The cooling of compact stars”
[10] Thorne, 1977, “The relativistic equations of stellar structure and evolution”
[11] Shapiro & Teukolsky, “Black Holes, White Dwarfs, and Neutron Stars”
[12] 小山勝ニ, 嶺重慎, “ブラックホールと高エネルギー現象”