Table of contents
中性子星の振動
実際の中性子星は固体クラストや強い磁場、超流動や高速自転などの特徴を持つため、中性子星の振動モードは複雑を極めます。 加えて、中性子星は一般相対論的な効果が重要となる天体であるため、一般相対論の枠組みを用いた振動の扱いが必要となります。 例えば、中性子星の振動により重力波が発生し、それが無限遠に飛び去ることで中性子星振動が減衰する効果などが現れます。 そこでここでは、このような複雑な物理は考えず、中性子星の微小振幅振動を普通の恒星の振動モード解析と同様に見ていきましょう。
普通の恒星の普通のモードは、一般的に p-, f-, g- の3つのモードに分類されます。 p-modeは流体の圧縮性(すなわち圧力)が復元力となって振動するモードで、その振動周波数は高周波となる傾向にあります。 次に、g-modeは浮力(すなわち重力)が復元力となって振動するモードで、p-modeに比べて低周波となります。 恒星が高速回転している場合、コリオリ力が復元力として働く回転モードと慣性モードが現れます。 さらに固体クラストが存在する場合、音波がクラスト中を伝播する効果も現れます。 そして強磁場がある場合、アルヴェーン波による振動も考慮する必要があります。
回転なし・磁場なしの通常の恒星の通常の振動モード
ここでは簡単のため、振動は断熱とし、粘性は考えないとしましょう。 さらに恒星は高速自転も磁場もないとして、重力もニュートン重力で考えることにします。 すると、この系を記述する方程式は、以下で与えられます。
\[\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \mathbf{v}) = 0 \tag{1}\] \[\rho \frac{d \mathbf{v}}{dt} = - \nabla P - \rho \nabla \Phi \tag{2}\] \[\nabla^2 \Phi = 4\pi G \rho \tag{3}\] \[\rho T \frac{ds}{dt} = \rho \epsilon - \nabla \cdot \mathbf{F} \tag{4}\] \[\mathbf{F}_\mathrm{rad} = -\lambda_\mathrm{rad} \nabla T \tag{5}\]ここで\(\Phi\)は重力ポテンシャル、\(s\)は単位質量あたりのエントロピー、\(\epsilon\)はエネルギー生成率、\(\mathbf{F}_\mathrm{rad}\)は放射によるエネルギー流束です。 そして\(\mathbf{F} = \mathbf{F}_\mathrm{rad} + \mathbf{F}_\mathrm{conv}\)であり、\(\mathbf{F}_\mathrm{conv}\)は対流によるエネルギー流束を表します。
断熱な振動を仮定し、さらに重力ポテンシャルの摂動は無視できるとしましょう。 密度・速度・圧力の摂動量をそれぞれ\(\rho', \mathbf{v}', P'\)し、(1), (2), (4)式を線形化していきましょう。 (1)式から
となります。 (2)式の左辺は
\[\begin{align} (\rho + \rho' )\frac{d}{dt} (\mathbf{v} + \mathbf{v}') &= \rho \left[ \frac{\partial}{\partial t} + \{ (\mathbf{v} + \mathbf{v}') \cdot \nabla \} \right] (\mathbf{v} + \mathbf{v}')+ \rho' \frac{d \mathbf{v}}{dt} \notag \\ &= \rho \left[ \frac{\partial \mathbf{v}}{\partial t} + \{ (\mathbf{v} + \mathbf{v}' )\cdot \nabla \} \mathbf{v} \right] + \rho \left\{ \frac{\partial \mathbf{v}'}{\partial t} + (\mathbf{v} \cdot \nabla) \mathbf{v}'\right\} + \rho' \frac{d \mathbf{v}}{dt} \notag \\ &= \rho \frac{d \mathbf{v}}{dt} + \rho' \frac{d \mathbf{v}}{dt} + \rho \left\{ \frac{\partial \mathbf{v}'}{\partial t} + (\mathbf{v}' \cdot \nabla) \mathbf{v} + (\mathbf{v} \cdot \nabla) \mathbf{v}'\right\} \notag \end{align}\]のようになるため、最終的に
\[\rho' \frac{d \mathbf{v}}{dt} + \rho \left\{ \frac{\partial \mathbf{v}'}{\partial t} + (\mathbf{v}' \cdot \nabla) \mathbf{v} + (\mathbf{v} \cdot \nabla) \mathbf{v}'\right\} = - \nabla P' - \rho' \nabla \Phi \tag{7}\]を得ます。断熱的な摂動であるとして、\(T ds = dQ = 0\)とすると
\[\begin{align} \frac{dQ}{dt} &= \frac{de}{dt} + P \frac{dV}{dt} = \frac{dP}{dt} \left( \frac{de}{dP}\right)_\rho + \frac{d\rho}{dt} \left(\frac{de}{d\rho} \right)_P + P \frac{d}{dt} \left( \frac{1}{\rho} \right) \notag \\ &= \frac{dP}{dt} \left( \frac{de}{dP}\right)_\rho + \frac{d\rho}{dt} \left(\frac{de}{d\rho} \right)_P - \frac{P}{\rho^2} \frac{d \rho}{dt} = \left( \frac{de}{dP} \right)_\rho \left\{ \frac{dP}{dt} - \frac{\frac{P}{\rho^2} - \left( \frac{de}{d\rho} \right)_P}{\left( \frac{de}{dP}\right)_P}\frac{d\rho}{dt}\right\} = 0 \notag \end{align}\]より
\[\frac{dP}{dt} = \frac{\frac{P}{\rho^2} - \left( \frac{de}{d\rho} \right)_P}{\left( \frac{de}{dP}\right)_P}\frac{d\rho}{dt} \equiv \left( \frac{\partial P}{\partial \rho} \right)_\mathrm{ad} \frac{d\rho}{dt}\]となります。 これを\(P \rightarrow P + P', \rho \rightarrow \rho + \rho'\)として、線形化しましょう。
\[\begin{aligned} \frac{d}{dt} (P + P') &= \frac{\partial P}{\partial t} + \{ (\mathbf{v} + \mathbf{v}') \cdot \nabla \} P + \frac{\partial P'}{\partial t} + (\mathbf{v} \cdot \nabla) P' \\ &= \frac{\partial P}{\partial t} + ( \mathbf{v} \cdot \nabla) P + \frac{\partial P'}{\partial t} + (\mathbf{v}' \cdot \nabla) P + (\mathbf{v} \cdot \nabla) P' \end{aligned}\]より、最終的に
\[\frac{\partial P'}{\partial t} + (\mathbf{v}' \cdot \nabla) P + (\mathbf{v} \cdot \nabla) P' = \left( \frac{\partial P}{\partial \rho} \right)_\mathrm{ad} \left( \frac{\partial \rho'}{\partial t} + (\mathbf{v}' \cdot \nabla) \rho + (\mathbf{v} \cdot \nabla) \rho' \right) \tag{8}\]を得ます。
ここで摂動量の時間依存性は\(e^{i\omega t}\)であるとし、さらに平衡状態は\(\mathbf{v}=\mathbf{0}\)かつ球対称であるとしましょう。 最後に\(\mathbf{v}' = i\omega \boldsymbol{\xi}\)のように、変位ベクトル\(\boldsymbol{\xi}\)を定めると
平衡状態では、\(-\nabla P - \rho \nabla \Phi = \mathbf{0}\)より
\[(7) \ \Longrightarrow \ i \omega \rho \frac{\partial \boldsymbol{\xi}}{\partial t} = - \nabla P' - \rho' \nabla \Phi \ \Longrightarrow \ -\omega^2 \boldsymbol{\xi} + \frac{1}{\rho} \nabla P' - \frac{\rho'}{\rho^2} \nabla P = \mathbf{0} \tag{10}\](8)式の左辺は
\[\frac{\partial \rho'}{\partial t} + (\mathbf{v}' \cdot \nabla) \rho + (\mathbf{v} \cdot \nabla) \rho' = i\omega \rho' + i\omega (\boldsymbol{\xi} \cdot \nabla) \rho = i\omega \rho \left( \frac{\rho'}{\rho} + \xi_r \frac{d\ln \rho}{dr} \right)\]のように整理されます。 途中、平衡状態が球対称であることから、\(\rho(r)\)としました。 右辺にも同様の変形を行うと
\[\begin{align} (8) & \Longrightarrow \ P \left( \frac{P'}{P} + \xi_r \frac{d\ln P}{dr} \right) = \left( \frac{\partial P}{\partial \rho}\right)_\mathrm{ad} \rho \left( \frac{\rho'}{\rho} + \xi_r \frac{d\ln \rho}{dr} \right) \notag \\ & \Longrightarrow \ \frac{P'}{P} + \xi_r \frac{d\ln P}{dr} = \Gamma_1 \left( \frac{\rho'}{\rho} + \xi_r \frac{d\ln \rho}{dr} \right) \tag{11} \end{align}\]途中
\[\Gamma_1 \equiv \left( \frac{\partial \ln P}{\partial \ln \rho}\right)_\mathrm{ad} = \frac{\rho}{P} \left( \frac{\partial P}{\partial \rho}\right)_\mathrm{ad} \tag{12}\]としました。
球対称な天体について考えるため、以降では極座標系 \((r, \theta, \varphi)\)を用いることにしましょう。 そして、変位ベクトル\(\boldsymbol{\xi}\)を、以下のように\(r\)と\((\theta, \varphi)\)で変数分離してみます。
ここで\(Y_\ell^m = Y_\ell^m (\theta, \varphi)\)は球面調和関数であり
\[\nabla_H = \mathbf{e}_\theta \frac{\partial}{\partial \theta} + \mathbf{e}_\varphi \frac{1}{\sin \theta} \frac{\partial}{\partial \varphi} \tag{14}\]です。 さらに
\[\mathbf{e}_r \cdot (\nabla_H Y_\ell^m) = \nabla_H Y_\ell^m \cdot (\mathbf{e}_r \times \nabla_H Y_\ell^m) = \mathbf{e}_r \cdot (\mathbf{e}_r \times \nabla_H Y_\ell^m) = 0 \tag{15}\]が成り立ちます。 またスカラー量の摂動については
\[P' = P_A'(r) Y_\ell^m, \quad \rho' = \rho_A'(r) Y_\ell^m \tag{16}\]とします。 (10)式より
\[\begin{align} &-\omega^2 \{\xi_r \mathbf{e}_r + \xi_H \nabla_H Y_\ell^m + \xi_T (\mathbf{e}_r \times \nabla_H Y_\ell^m )\} + \frac{1}{\rho} \left( \mathbf{e}_r \frac{\partial}{\partial r} + \frac{1}{r} \nabla_H \right) P_A' Y_\ell^m - \frac{\rho_A' Y_\ell^m}{\rho^2} \left( \mathbf{e}_r \frac{\partial}{\partial r} + \frac{1}{r} \nabla_H \right) P \notag \\ &= \left( -\omega^2 \xi_r + \frac{1}{\rho} \frac{dP'}{dr} - \frac{\rho'}{\rho^2} \frac{dP}{dr} \right) \mathbf{e}_r + \left( - \omega^2 \xi_H + \frac{P_A'}{r\rho} \right) \nabla_H Y_\ell^m - \omega^2 \xi_T (\mathbf{e}_r \times \nabla_H Y_\ell^m) = \mathbf{0} \notag \end{align}\]のように計算されるため、各成分から
\[-\omega^2 \xi_r + \frac{1}{\rho} \frac{dP'}{dr} - \frac{\rho'}{\rho^2} \frac{dP}{dr} = 0 \tag{17}\] \[-\omega^2 \xi_H + \frac{P_A'}{r \rho} = 0 \tag{18}\] \[-\omega^2 \xi_T = 0 \tag{19}\]とわかります。 ここから、\(\omega \neq 0\)の波では、常に\(\xi_T = 0\)であることがわかります。
\(\boldsymbol{\xi} = \xi_r \mathbf{e}_r + \xi_H \nabla_H Y_\ell^m\)をspheroidal modes、そして\(\boldsymbol{\xi} = \xi_T (\mathbf{e}_r \times \nabla_H Y_\ell^m)\)をtoroidal modesと呼びます。 自転していない恒星では、spheroidal modesとtoroidal modesは2つに分離することができ、さらに先ほどの議論から\(\xi_T = 0\)となることがわかります。 \(\omega =0\)では任意の\(\xi_T\)が許されることから、自転のない恒星では、\(\omega = 0\)のtoridal modesが縮退していると考えることもできます。
\(\omega \neq 0\)に対する式変形を進めていきましょう。 (17)式より
ここで、(2)式と、平衡状態では常に\(\mathbf{v}=0\)であることから
\[\frac{dP}{dr} = \rho \frac{d\Phi}{dr} = \frac{GM_r \rho}{r^2} = \rho g \quad \left( g = \frac{GM_r}{r^2} \right) \tag{20}\]のようになります。 途中、中心から距離\(r\)の位置での重力ポテンシャルを\(\Phi = -\frac{GM_r}{r}\)としました。 さらに(11)式より
\[\frac{\rho'}{\rho} = \frac{1}{\Gamma_1} \left( \frac{P'}{P} + \xi_r \frac{d\ln P}{dr}\right) - \xi_r \frac{d \ln \rho}{dr} \tag{21}\]であることを用いると
\[\begin{align} \frac{dP'}{dr} &= \rho \omega^2 \xi_r + \frac{\rho g}{\Gamma_1} \left( \frac{P'}{P} + \xi_r \frac{d\ln P}{dr}\right) - \xi_r \rho g \frac{d\ln \rho}{dr} \notag \\ &= \rho \xi_r \left\{ \omega^2 - g \left( \frac{d\ln \rho}{dr} - \frac{1}{\Gamma_1} \frac{d\ln P}{dr} \right) \right\} + \frac{1}{\Gamma_1} \frac{d\ln P}{dr} P' \tag{22} \end{align}\]のようになります。 ここで、以下の量を定義しましょう。
\[N^2 = -gA, \quad A \equiv \frac{d \ln \rho}{dr} - \frac{1}{\Gamma_1} \frac{d \ln P}{dr} \tag{23}\]この\(N\)はブラント・バイサラ振動数 (Brunt-Väisälä frequency)と呼ばれ、恒星物理に限らず、重力と浮力を復元力とした波動現象において現れる振動数です。 これを用いると
\[\frac{dP_A'}{dr} = \frac{1}{\Gamma_1} \frac{d\ln P}{dr} P' + \rho (\omega^2 - N^2) \xi_r \tag{24}\]のように整理されます。 さらに(9)式より
\[\rho' + \nabla \cdot {\rho \boldsymbol{\xi}} = \rho' + \boldsymbol{\xi} \cdot (\nabla \rho) + \rho (\nabla \cdot \boldsymbol{\xi}) = 0\]第三項を計算しましょう。
\[\begin{aligned} \nabla \cdot \boldsymbol{\xi} &= \left( \mathbf{e}_r \frac{\partial}{\partial r} + \frac{1}{r} \nabla_H \right) \cdot \{ \xi_r \mathbf{e}_r + \xi_H \nabla_H Y_\ell^m + \xi_T (\mathbf{e}_r \times \nabla_H Y_\ell^m) \} = \frac{d \xi_r}{dr} + \frac{\xi_H}{r} \nabla_H^2 Y_\ell^m \\ &= \frac{d \xi_r}{dr} - \frac{\xi_H \ell (\ell + 1)}{r} Y_\ell^m \end{aligned}\]最後の等号では、球面調和関数の性質\(\nabla_H^2 Y_\ell^m = - \ell (\ell + 1) Y_\ell^m\)を用いました。 以上より
\[\begin{aligned} \rho' + \xi_r \frac{d\rho}{dr} + \rho \frac{d\xi_r}{dr} - \frac{\rho \xi_H \ell (\ell + 1)}{r} Y_\ell^m &\underbrace{=}_{(21)} \frac{\rho}{\Gamma_1} \left( \frac{P'}{P} + \xi_r \frac{d\ln P}{dr}\right) - \rho \xi_r \frac{d\ln \rho}{dr} + \xi_r \frac{d\rho}{dr} + \rho \frac{d\xi_r}{dr} - \frac{\rho \xi_H \ell (\ell + 1)}{r} Y_\ell^m \\ &\underbrace{=}_{(18)} \frac{\rho}{\Gamma_1} \left( \frac{P'}{P} + \xi_r \frac{d\ln P}{dr}\right) + \rho \frac{d\xi_r}{dr} - \frac{\ell (\ell + 1) P_A'}{r^2 \omega^2} Y_\ell^m = 0 \end{aligned}\]となります。 さらに
\[S_\ell^2 \equiv \frac{\ell (\ell+1)}{r^2} a^2, \quad a^2 = \frac{\Gamma_1 P}{\rho} \tag{25}\]を用い、式を整理しましょう。 すると
\[\frac{d\xi_r}{dr} = \left( \frac{S_\ell^2}{\omega^2} - 1\right) \frac{P'}{\Gamma_1 P} - \frac{1}{\Gamma_1} \frac{d \ln P}{dr} \xi_r \tag{26}\]を得ます。 \(S_\ell\)はラム周波数 (Lamb frequency)と呼ばれ、音速が球面上の波長を横切る時間の逆数として定義されます。
周波数\(\omega\)の固有値問題として、(24), (26)式の連立微分方程式を適切な(恒星中心部と恒星表面での)境界条件で解くことで、どのような振動が存在するかを知ることができます。 \(N^2 >0\)の場合、安定した流体の浮力振動のために、エネルギーは輻射によって運ばれます (radiative regions。) 一方、\(N^2 < 0\)の場合、これは流体が上昇/下降を続ける対流層を表します (convective retions。) \(\omega^2 \gg N^2, S_\ell^2\)はp-modesであり、\(\omega^2 \ll N^2, S_\ell^2\)はg-modesです。
動径方向の脈動のみを考える場合
この場合、変位ベクトルは\(\boldsymbol{\xi} = \xi_r \mathbf{e}_r\)のように書かれます。 さらに、断熱的な動径方向脈動であると仮定すれば、以下の微分方程式を得ることができます。
\[\frac{d}{dr} \left\{ \Gamma_1 P \frac{1}{r^2} \frac{d}{dr} (r^2 \xi_r) \right\} - \frac{4}{r} \frac{dP}{dr} \xi_r + \omega^2 \rho \xi_r = 0 \tag{27}\]先程と同様、これを\(\omega^2\)の固有値問題として解けば良いでしょう。
自転が存在する場合
恒星が高速自転している場合、線形化された運動方程式は、次のような形になります。
\[-\omega^2 \boldsymbol{\xi} + 2i\omega \boldsymbol{\Omega} \times \boldsymbol{\xi} + \frac{1}{\rho} \nabla P' - \frac{\rho'}{\rho^2} \nabla P = \mathbf{0} \tag{28}\]第二項はコリオリ力によるものです。 コリオリ力の存在により、\(\omega^2 \neq 0\)でも\(\xi_T =0\)にならず、非ゼロの\(\xi_T\)が\(\xi_r, \xi_H\)と相互作用を起こします。
固体クラストの記述
固体クラスト中を波動が伝搬するのを記述するには、運動方程式を修正する必要があります。 具体的には、以下のようなモデルがあります。
\[-\omega^2 \boldsymbol{\xi} - \frac{1}{\rho} \nabla \cdot \boldsymbol{\sigma}' + \frac{\rho'}{\rho^2} \nabla \cdot \boldsymbol{\sigma} = \mathbf{0} \tag{29}\]ここで\(\boldsymbol{\sigma}\)は応力テンソルで、そのラグランジュ的な変分\(\delta \boldsymbol{\sigma}\)は歪みテンソル\(u_{ij}\)と以下のような関係にあります。
\[\delta \sigma_{ij} = (\Gamma_1 P u_{\ell \ell}) \delta_{ij} + 2 \mu \left( u_{ij} - \frac{1}{3} u_{\ell \ell} \delta_{ij} \right) \tag{30}\]ここで
\[u_{ij} = \frac{1}{2} \left( \frac{\partial \xi_i}{\partial x_j} + \frac{\partial \xi_j}{\partial x_i} \right), \quad u_{\ell \ell} = u_{11} + u_{22} + u_{33} = \nabla \cdot \boldsymbol{\xi} \tag{31}\]であり、\(\mu\)は固体クラストのせん断弾性係数(せん弾力を受けたときの変形のしにくさを表す係数)です。 ラグランジュ的な変分\(\delta \sigma_{ij}\)とオイラー的な摂動\(\sigma_{ij}'\)は、次の関係式で結ばれています。
\[\delta \sigma_{ij} = \sigma_{ij}' + \boldsymbol{\xi} \cdot \nabla \boldsymbol{\sigma} \tag{32}\]また、平衡状態では\(\sigma_{ij} = - P \delta_{ij}\)です。
磁場の効果
磁場を考慮する場合、摂動を受けた運動方程式には
\[- \omega^2 \boldsymbol{\xi} + \frac{1}{\rho} \nabla P' - \frac{\rho'}{\rho^2} \nabla P - \left[ \frac{(\nabla \times \mathbf{B}) \times \mathbf{B}}{4\pi \rho}\right]' = \mathbf{0} \tag{33}\]のように、最後の項が追加されます。 また\(\mathbf{B}'\)と\(\boldsymbol{\xi}\)の関係を与える、摂動を受けた誘導方程式は
\[\mathbf{B}' = \nabla \times (\boldsymbol{\xi} \times \mathbf{B}) \tag{34}\]で与えられます。
中性子星の脈動周波数スペクトル
中性子星が、表面の流体海洋・固体クラスト・流体コアからなる場合に、基準モードを計算した結果を見てみましょう。
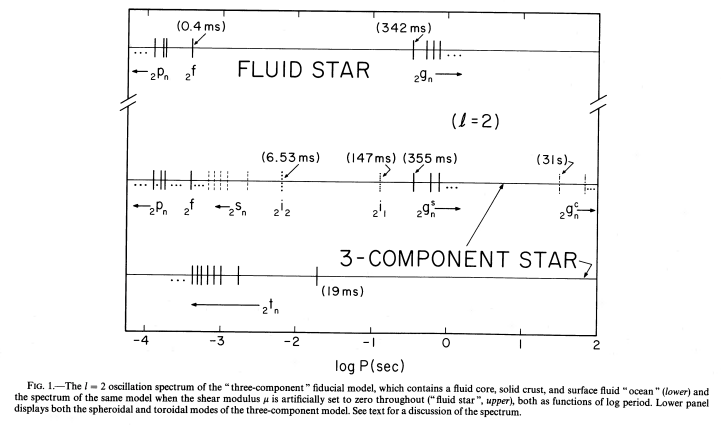
McDermott et al. (1988)より。3つの構成要素からなる中性子星モデルにおいて、\(\ell=2\)の振動スペクトルを図示したもの。
一番上の水平方向の直線は、流体中性子星モデルでの周波数スペクトルであり、固体クラストのせん断弾性係数をゼロとしたものです。 流体モデルでは、p-, f-, g-modeのみが存在します。 その下の2つの線は、3要素からなる中性子星モデルの振動スペクトルです。 そのうち、中央の線は流体領域と固体クラスト中を伝搬するspheroidal modesで、\({}_2 s_n\)は固体クラスト中を伝搬する音波を表しています。 \({}_s g_n\)はg-modeを表しますが、特に流体コアを伝搬するものを\({}_2 g_n^c\)、そして表面流体海洋を伝搬するものを\({}_2 g_n^s\)と分類します。 さらに3要素からなる中性子星では、その要素の境界面を伝搬するモード (interfacial modes)が存在します。 \({}_2 i_1, {}_2 i_2\)はそれぞれ、流体コアと固体クラスト間の境界面、固体クラストと流体海洋間の境界面を伝搬する大振幅モードを表しています。 そして一番下の直線が表すのは、固体クラスト中を伝搬するtoroidal modesです。
重力波放射によるr-mode不安定性
Andersson & Kokkotas (1998)によれば、自転する中性子星におけるr-modesは、重力波を放出することで不安定であることが知られています。 これはコリオリ力を復元力とする、回転により誘起されるr-modeです。 そのため、この振動周波数は自転スピン周波数\(\Omega\)に比例します。 そして、中性子星と一緒に回転する座標系における固有関数\(\boldsymbol{\xi}_T\)、周波数 \(\omega = \sigma + m \Omega\)は、\(\Omega \rightarrow 0\)の極限で、次のように与えられます。
\[\boldsymbol{\xi}_T \rightarrow T_\ell (r) \left( \frac{1}{\sin \theta} \frac{\partial Y_\ell^m}{\partial \varphi} \mathbf{e}_\theta - \frac{\partial Y_\ell^m}{\partial \theta} \mathbf{e}_\varphi \right), \quad \omega \rightarrow \frac{2m\Omega}{\ell (\ell + 1)} \tag{35}\]慣性系での周波数は
\[\sigma = \omega - m\Omega \rightarrow \left\{ \frac{2}{\ell (\ell + 1)} -1 \right\} m\Omega \tag{36}\]で与えられます。 有限の値の\(\Omega\)において、\(\omega\)を展開しましょう。
\[\frac{\omega}{\Omega} = \kappa_0 + \kappa_2 \Omega^2 + \cdots \tag{37}\]ここでr-modesの場合、\(\kappa_0 = 2m / \ell (\ell + 1)\)となります。 振動モードの減衰の時間スケールを、次のように定義します。
\[\frac{1}{\tau} = - \frac{1}{2E} \frac{dE}{dt} \tag{38}\]ここで
\[E = \frac{1}{2} \int \left\{ \rho \delta \mathbf{v} \cdot \delta \mathbf{v} + \left( \frac{\delta P}{\rho} + \delta \Phi \right) \delta \rho^\ast \right\} d^3 \mathbf{x} \tag{39}\]であり、\(\delta\)はオイラー的な摂動量を表しています。
この振動の減衰メカニズムには、いくつかあります。 代表的なものをいくつか見ていきましょう。
- シア粘性による散逸
ここで、\(\delta \sigma_{ij}\) = 0.5( \nabla_i \delta v_j + \nabla_j \delta v_i - (2/3) g_{ij} \delta \theta)、\(\delta \theta = \nabla \cdot \delta \mathbf{v}\)です。
- バルク粘性による散逸
- 質量流束からの重力波放射による散逸
ここで
\[\delta D_{\ell m} = \int \delta \rho r^\ell Y_\ell^{\ast m}, \quad N_\ell = \frac{4\pi G}{c^{2\ell + 1}} \frac{(\ell + 1) (\ell + 2)}{\ell (\ell - 1) \{(2\ell + 1) !!\}^2} \tag{43}\]です。
- 角運動量流束からの重力波放射による散逸
ここで
\[\delta J_{\ell m} = \frac2c \left( \frac{\ell}{\ell +1}\right)^{1/2} \int r^\ell (\rho \delta v_i + v_i \delta \rho) \frac{r \epsilon^{ijk}}{\sqrt{\ell (\ell +1)}} \nabla_j Y_\ell^{\ast m} \nabla_k r d^3\mathbf{x} \tag{45}\]です。 (35)式から、\(\ell \geq 2\)のとき、\(\sigma < 0\)となり、不安定であることがわかります。 温度\(T\)に依存する\(\eta, \zeta\)の適切な表現を用いることで、\(\Omega, T\)の関数として減衰時間スケール\(\tau\)を計算することができます。 \(\Omega\)の最低次では、モードの減衰時間スケールは以下のように書かれます。
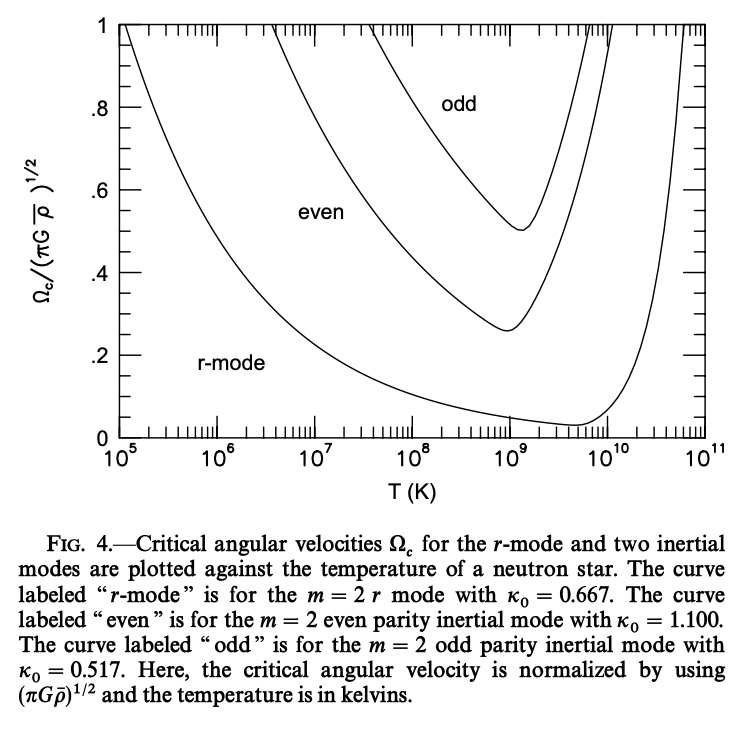
\[\frac{1}{\tau} = \frac{1}{\tilde{\tau}_S} \left( \frac{10^9 \mathrm{K}}{T}\right)^2 + \frac{1}{\tilde{\tau}_B} \left( \frac{T}{10^9 \mathrm{K}}\right)^2 \left( \frac{\pi G \bar{\rho}}{\omega^2}\right) + \sum_{\ell=2}^\infty \frac{1}{\tilde{\tau}_{J, \ell}} \left( \frac{\Omega^2}{\pi G \bar{\rho}}\right)^{\ell +1} + \sum_{\ell=2}^\infty \frac{1}{\tilde{\tau}_{D, \ell}} \left( \frac{\Omega^2}{\pi G \bar{\rho}}\right)^{\ell +2} \tag{46}\]ここで、\(\bar{\rho}\)は、星の平均密度です。 \(T-\Omega\)平面における安定・不安定の境界を探るためには、\(1/\tau = 0\)となる臨界スピン振動数\(\Omega_c (T)\)を計算します。 結果を下図に示します。
この図は、ポリトロープモデルに対し、\(m=\ell=2\)のr-modeと2つの慣性モードについて計算したものです。
固体クラストがある場合
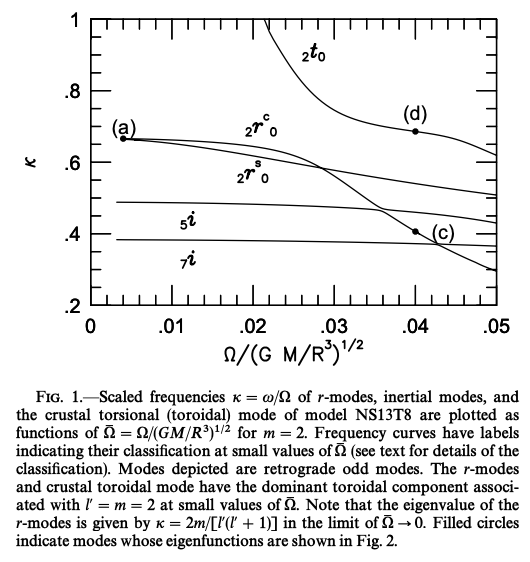
表面の流体海洋・固体クラスト・流体コアの3要素からなる中性子星モデルに対し、\(\Omega\)の関数として\(\kappa \equiv \omega / \Omega\)を計算した論文の結果を以下に示します。
この場合、表面の流体海洋に閉じ込められているr-modeと、流体コアに閉じ込められているr-modeの、2つが存在します。 これらは\(\Omega \rightarrow 0\)で同じ\(\kappa\)に収束することがわかります。 またr-modes間と、r-modeと慣性モードの間に、avoided crossing (擬交差)があることがわかります。 Toroidalなクラストモードの周波数は、\(\Omega\)に対する依存性が弱く、\(\Omega \rightarrow 0\)で\(\kappa = \omega / \Omega\)が発散します。 \(\Omega\)が大きくなると、クラストモードとコア内のr-modeが擬交差を起こしそうであることもわかります。
参考文献
[1] McDermott et al., 1988, “Nonradial Oscillations of Neutron Stars”
[2] Andersson & Kokkotas, 1998, “Towards gravitational wave asteroseismology”
[3] Yoshida & Lee, 2000, “Inertial Modes of Slowly Rotating Isentropic Stars”
[4] Yoshida & Lee, 2001, “r-Modes of Neutron Stars with a Solid Crust”
[5] Cunha, 2017, “Theory of Stellar Oscillations”
[6] Cox, “Theory of Stellar Pulsation”