Table of contents
軸対称モデル
球対称モデルは、球状星団や楕円銀河を扱いためのものでした。 ここでは円盤銀河のような、薄い円盤型の質量モデルを見ていきましょう。 ただし、ここで扱うのは軸対称なものであり、銀河の持つ渦状腕などは考慮しないものとします。
非常に薄い円盤モデル (razor-thin disk or zero-thickness disk)
銀河を形成する質量が\(z=0\)平面のみに存在すると仮定します。 すなわち、その質量分布が
\[\rho (R, z) = \Sigma (R) \delta (z) \tag{1}\]のように書けるものとします。 ここで\(\Sigma(R)\)は表面密度です。 また\(\delta(z)\)はデルタ関数ですが、\(\delta(0)=1\)であるとします。
ポアソン方程式、重力ポテンシャルと質量密度は
の関係にあります。
\(z \neq 0\)の場合
ここで\(z \neq 0\)の場合を考えてみましょう。 するとデルタ関数の性質より
\[\frac{1}{R} \frac{\partial}{\partial R} \left( R \frac{\partial \Phi}{\partial R}\right) + \frac{\partial^2 \Phi}{\partial z^2} = 0 \tag{3}\]のようになります。 これを解くために\(\Phi(R, z) = J(R) Z (z)\)のように、変数分離をしましょう。 これを代入すると
\[\frac{Z}{R} \frac{d}{d R} \left( R \frac{dJ}{dR}\right) + J \frac{d^2 Z}{dz^2} = 0 \ \Longrightarrow \ \frac{1}{JR} \frac{d}{dR} \left( R \frac{dJ}{dR}\right) = - \frac{1}{Z} \frac{d^2 Z}{dz^2} = -k^2 \tag{4}\]左辺は\(R\)のみの関数、右辺は\(z\)のみの関数であるため、これらを定数\(-k^2\)であるとしました。 すると\(z\)方向に対しては
\[\frac{d^2 Z}{dz^2} = k^2 Z \ \Longrightarrow \ Z = C e^{\pm kz} \tag{5}\]のように解くことができます。 ここで\(C\)は積分定数です。 続いて\(R\)方向は
\[\frac{1}{R} \frac{\partial}{\partial R} \left( R \frac{dJ}{dR}\right) + k^2 J = 0 \tag{6}\]のようになります。 この方程式を解くために\(u \equiv kR\)とおくと
\[\frac{1}{u} \frac{d}{du} \left( u \frac{dJ}{du}\right) + J = 0 \tag{7}\]のように整理されます。 すると、この方程式は\(n=0\)のベッセルの微分方程式になっています。 よって(7)式の解は\(J = J_0(u)\)で与えられます。 以上から、(3)式の解は
\[\Phi(R, z) = J_0 (kR) e^{\pm kz} \tag{8}\]と求まります。 重力ポテンシャルを、\(\vert z \vert \rightarrow \infty\)で\(\Phi \rightarrow 0\)になるように計算しましょう。 さらに、\(k > 0\)のみを考えると
\[\left\{ \begin{array}{ll} e^{-kz} & (z \geq 0) \\ e^{kz} & (z<0) \end{array}\right. \ \Longrightarrow \ \Phi (R, z) = J_0 (kR) e^{-k \vert z \vert} \tag{9}\]が妥当であるとわかります。
\(z = 0\)の場合
次に、\(z=0\)について考えることにしましょう。 下図のように、\(z=0\)を挟んで\(z\)方向の重力が不連続に変化することを考慮に入れて、計算を行います。
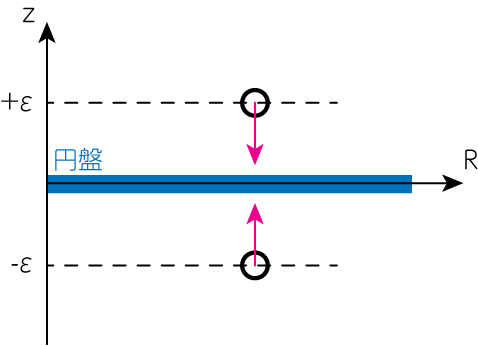
\(z=\pm \epsilon\)における\(z\)方向の重力を計算し、その\(\epsilon \rightarrow 0\)の極限を取ります。 すると
\[\lim_{\epsilon \rightarrow 0} \left. \left( -\frac{\partial \Phi}{\partial z}\right) \right|_{z=\epsilon} = \lim_{\epsilon \rightarrow 0} k J_0 (kR) e^{-k\epsilon} = k J_0 (kR) \tag{10}\] \[\lim_{\epsilon \rightarrow 0} \left. \left( -\frac{\partial \Phi}{\partial z}\right) \right|_{z=-\epsilon} = \lim_{\epsilon \rightarrow 0} (-k) J_0(kR) e^{-k \epsilon} = -k J_0 (kR) \tag{11}\]この重力の不連続性を、\(\Sigma(R)\)と結びつけましょう。 (2)式を\([-\epsilon, \epsilon]\)で積分すると
\[\begin{align} (右辺) &= \int_{-\epsilon}^\epsilon \frac{1}{R} \frac{\partial}{\partial R} \left( R \frac{\partial \Phi}{\partial R}\right) dz + \int_{-\epsilon}^\epsilon \frac{\partial^2 \Phi}{\partial z^2} dz = \int_{-\epsilon}^\epsilon \frac{1}{R} \frac{\partial}{\partial R} \left( R \frac{\partial \Phi}{\partial R}\right) dz + \left( \left. \frac{\partial \Phi}{\partial z} \right|_{z=\epsilon} - \left. \frac{\partial \Phi}{\partial z} \right|_{z=-\epsilon} \right) \notag \\ &\xrightarrow{\epsilon \rightarrow 0} - 2k J_0 (kR) \tag{12} \end{align}\] \[(左辺) = 4\pi G \Sigma (R) \int_{-\epsilon}^\epsilon \delta(z) dz = 4\pi G \Sigma (R) \tag{13}\]のようになります。 途中、右辺第一項は\(\epsilon \rightarrow 0\)でゼロとなることを用いました。 よって
\[\Sigma_k (R) = - \frac{k}{2\pi G} J_0(kR) \tag{14}\]を得ます。 ここで定数\(k\)の依存性が存在することを明示的に表すために、\(\Sigma_k\)のように表記しました。 また、ここまでの計算から\(\Sigma_k\)に対応する重力ポテンシャルが\(\Phi_k = J_0 (kR) e^{-k\vert z \vert}\)であることもわかります。
ポアソン方程式は線形であるため、解を重ね合わせたものもまた解となります。 よって
もまた、ポアソン方程式の解です。 ここで\(S(k)\)は、\(\Sigma_k\)の重みを表す関数です。 この式はハンケル変換 (Hankel transform)として知られています。 この逆変換から、適当な表面密度\(\Sigma (R)\)に対する重み\(S(k)\)が
\[S(k) = - 2\pi G \int_0^\infty R \Sigma (R) J_0 (kR) dR \tag{16}\]のように求まります。 こうして求めた\(S(k)\)を用いることで
\[\Phi (R, z) = \int_0^\infty S(k) \Phi_k(R, z) dk \tag{17}\]を計算すれば、こちらが与えた\(\Sigma (R)\)に対応する重力ポテンシャル\(\Phi (R, z)\)を計算することができます。 また回転速度は
\[\begin{align} &\frac{v_c^2}{R} = \left. \frac{\partial \Phi}{\partial R} \right|_{z=0} \notag \\ &\Longrightarrow \ v_c^2 = R \int_0^\infty S(k) \left. \frac{\partial \Phi_k}{\partial R} \right|_{z=0} dk \underbrace{=}_{u = kR} R \int_0^\infty k S(k) \frac{d J_0 (u)}{d u} dk = - R \int_0^\infty k S(k) J_1 (kR) dk \tag{18} \end{align}\]のように計算されます。 途中、ベッセル関数において成り立つ漸化式\(\frac{dJ_0}{du} = -J_1 (u)\)を用いました。 (16)式から\(S(k)\)を求めれば、同様に回転速度を求めることが可能であるとわかります。
指数円盤モデル (exponential disk)
ここでは、以下のような面密度の円盤を考えることにしましょう。
\[\Sigma (R) = \Sigma_0 e^{-R/h} \tag{19}\]中心からの距離\(R\)に指数依存していることから、このモデルを指数円盤モデルと呼びます。 これは中心部ほど明るく、中心から離れると急激に明るさが減衰する、円盤銀河の高度分布を良く再現するものとして考えられてきました。 (19)式を(16)式に代入すると
\[\begin{align} S(k) &= -2\pi G \Sigma_0 \int_0^\infty R J_0 (kR) e^{-R/h} dR \underbrace{=}_{\alpha = 1/h} 2\pi G \Sigma_0 \frac{\partial}{\partial \alpha} \int_0^\infty J_0(kR) e^{-\alpha R} dR \notag \\ &= 2\pi G \Sigma_0 \frac{\partial}{\partial \alpha} \frac{1}{\sqrt{\alpha^2 + k^2}} \tag{20} \end{align}\]のように計算されます。 途中、ベッセル関数のラプラス変換を用いました。 さらにこれを(17)式に代入すると
\[\Phi (R, z) = 2\pi G \Sigma_0 \frac{\partial}{\partial \alpha} \int_0^\infty \frac{J_0 (kR) e^{-k \vert z \vert}}{\sqrt{\alpha^2 + k^2}} dk \tag{21}\]です。 特に\(z=0\)では
\[\begin{align} \Phi (R, 0) &= 2\pi G \Sigma_0 \frac{\partial}{\partial \alpha} \{ I_0 (\alpha R / 2) K_0 (\alpha R / 2) \} \notag \\ &= \pi G \Sigma_0 R \{ I_1(\alpha R / 2) K_0 (\alpha R / 2) - I_0 (\alpha R / 2) K_1 (\alpha R / 2) \} \tag{22} \end{align}\]と計算できます。 ここで\(I_n, K_n\)はそれぞれ、第一種と第二種の修正ベッセル関数です。 途中、ベッセル関数と同様に、これらは\(\frac{dI_0(x)}{dx} = I_1(x), \frac{dK_0(x)}{dx} = -K_1 (x)\)が成り立つことも用いました。 同様に\(v_c\)を計算しましょう。
\[\begin{align} v_c^2 &= R \frac{\partial \Phi (R, 0)}{\partial R} \notag \\ &= \pi G \Sigma_0 R \left[ I_1 (\alpha R/ 2) K_0 (\alpha R /2) - I_0 (\alpha R/ 2) K_1 (\alpha R /2) + R \frac{\partial}{\partial R} \left\{ I_1 (\alpha R/ 2) K_0 (\alpha R /2) - I_0 (\alpha R/ 2) K_1 (\alpha R /2) \right\} \right] \tag{23} \end{align}\]\(y = \alpha R / 2\)とおくと、\(\frac{\partial}{\partial R} = \frac{\alpha}{2} \frac{\partial}{\partial y}\)より
\[v_c^2 = \pi G \Sigma_0 R \left\{ I_1 K_0 - I_1 K_0 + \frac{\alpha R}{2} \left( \frac{d I_1}{d y} K_0 + I_1 \frac{d K_0}{d y} - \frac{d I_0}{d y} K_1 - I_0 \frac{d K_1}{d y} \right)\right\} \tag{24}\]修正ベッセル関数の公式\(\frac{dI_1}{dy} = I_0 - \frac{I_1}{y}, \frac{dK_1}{dy} = - K_0 - \frac{K_1}{y}\)より
\[\begin{align} v_c^2 &= \pi G \Sigma_0 R \left[ I_1 K_0 - I_1 K_0 + \frac{\alpha R}{2} \left\{ 2 (I_0 K_0 - I_1 K_1) - \frac{1}{y} (I_1 K_0 - I_0 K_1)\right\} \right] \notag \\ &= \pi G \Sigma_0 \frac{R^2}{h} (I_0 K_0 - I_1 K_1) \tag{25} \end{align}\]この回転速度を図示すると、以下のようになります。
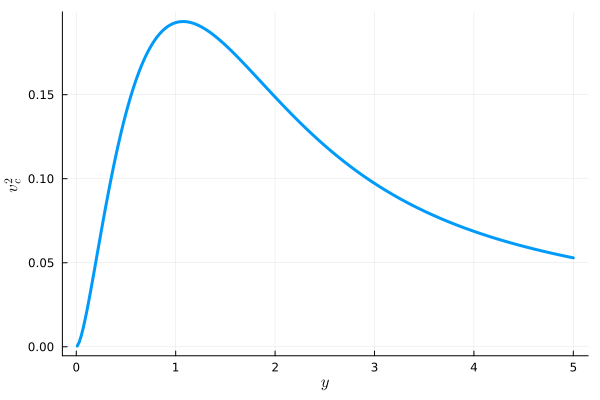
この図からわかるように、このモデルは円盤銀河のflat rotationを再現できず、\(y = \frac{R}{2h} \approx 1\)程度でピークを持つような回転速度となります。
メステル円盤 (Mestel disk)
このモデルでは、円盤の面密度分布を次のように与えます。
\[\Sigma_\mathrm{Mestel} (R) = \frac{C^2}{2\pi GR} \tag{26}\]ここで\(C\)は定数とします。 この場合、\(S(k)\)は
\[S(k) = -2\pi G \int_0^\infty R \frac{C^2}{2\pi GR} J_0 (kR) dR = - C^2 \int_0^\infty J_0 (kR) dR = - \frac{C^2}{k} \tag{27}\]と計算できます。 途中、\(\int_0^\infty J_n (x) dx =1\)であることを用いました。 すると、この面密度分布に対応する重力ポテンシャルを求めるには
\[\Phi (R, z) = - \int_0^\infty \frac{C^2}{k} J_0 (kR) e^{-k \vert z \vert} dk \tag{28}\]を計算すれば良いとわかります。 ここで
\[\frac{\partial}{\partial \vert z \vert} \int_0^\infty \frac{J_0(kR)}{k} e^{-k\vert z \vert} dk = - \int_0^\infty e^{-k \vert z \vert} J_0 (kR) dk \underbrace{=}_{ベッセル関数のラプラス変換} \frac{1}{\sqrt{R^2 + z^2}} \tag{29}\]と
\[\frac{\partial}{\partial z} \ln(\sqrt{R^2 + z^2} + z) = \frac{1}{\sqrt{R^2 + z^2} + z} \left(\frac{z}{\sqrt{R^2 + z^2}} + 1\right) = \frac{1}{\sqrt{R^2 + z^2}} \tag{30}\]より
\[\Phi(R, z) = C^2 \ln(\sqrt{R^2 + z^2} + z) \tag{31}\]と求まります。 さらに、回転速度は(18)式より
\[v_c^2 = R \int_0^\infty C^2 J_1(kR) dk \underbrace{=}_{\int_0^\infty J_n(x) dx = 1} C^2 \tag{32}\]となります。 メステル円盤モデルでは、回転速度が定数となり、銀河のflat rotationを再現できることがわかります。
クズミンモデル (Kuzmin model)
同じような薄い円盤モデルの一つとして、クズミンモデルと呼ばれるものがあります。 先ほどのように特殊関数を用いずとも解析的に諸物理量を求めることができ、計算が容易に扱えることが特徴です。 このモデルは、以下のような重力ポテンシャルで表現されます。
\[\Phi (R, z) = - \frac{GM}{\sqrt{R^2 + (\vert z \vert + a)^2}} \tag{33}\]\(a=0\)のとき、このモデルは
\[\Phi (R, z) = - \frac{GM}{\sqrt{R^2 + z^2}} = - \frac{GM}{r} \tag{34}\]のように、原点に質量\(M\)の質点が存在する場合の重力ポテンシャルに等しくなります。 またこの重力ポテンシャルは、\(z \geq 0\)では\((R, z) = (0, -a)\)に質量\(M\)の質点が存在する重力ポテンシャルに一致し、\(z<0\)では\((R, z)= (0, a)\)に質点が存在する重力ポテンシャルとなります。
よって、\(z \neq 0\)では対応する質量密度分布はゼロと考えて良いでしょう。 この議論から、
\[\rho(R, z) = \Sigma (R) \delta (z) \tag{35}\]のように書くことができます。 これは先ほどの非常に薄い円盤モデルで議論したものと同じ形です。 よって\(z=0\)での重力の不連続性を、面密度と関連づけることにしましょう。 \(z > 0\)では
\[\frac{\partial \Phi}{\partial z} = \frac{GM(z+a)}{(R^2 + (z+a)^2)^{3/2}} \xrightarrow{z \rightarrow +0} \frac{GMa}{(R^2 + a^2)^{3/2}} \tag{36}\]そして\(z<0\)では
\[\frac{\partial \Phi}{\partial z} = -\frac{GM(a-z)}{(R^2 + (a-z)^2)^{3/2}} \xrightarrow{z \rightarrow -0} - \frac{GMa}{(R^2 + a^2)^{3/2}} \tag{37}\]です。 (14)式を求めたときの計算から
\[\Sigma_\mathrm{Kuzmin} (R) = \frac{Ma}{2\pi (R^2 + a^2)^{3/2}} \tag{38}\]と求まります。 さらに、回転速度は
\[v_c^2 = R \left. \frac{\partial \Phi}{\partial R}\right|_{z=0} = \frac{GM R^2}{(R^2 + a^2)^{3/2}} \tag{39}\]と計算されます。 (39)式からわかるように、\(R \gg a\)では\(v_c^2 \propto R^{-1}\)となり、このモデルも銀河のflat rotationを再現できません。
宮本・永井ポテンシャル
先ほどまでのモデルは円盤が非常に薄く、その厚さが無視できる場合の円盤の重力ポテンシャルでした。 ここでは、円盤の厚さが有限な場合の重力ポテンシャルについて説明します。 特に、有名なMiyamoto & Nagai (1975)で示された銀河の重力ポテンシャルモデル、宮本・永井ポテンシャルを以下に示します。
\[\Phi_\mathrm{MN} (R, z) = - \frac{GM}{\sqrt{R^2 + (a + \sqrt{z^2 + b^2})^2}} \tag{40}\]このモデルは、\(a \rightarrow 0\)で球対称なプラマーモデル、\(b \rightarrow 0\)で薄い円盤のクズミンモデルとなります。 このことから、パラメータ\(a, b\)を調整することで、球対称と円盤の両方を取り入れることが可能です。 (40)式に対応する密度分布を求めましょう。 ポアソン方程式より
\[\nabla^2 \Phi_\mathrm{MN} (R, z) = \frac{1}{R} \frac{\partial}{\partial R} \left(R \frac{\partial \Phi_\mathrm{MN}}{\partial R} \right) + \frac{\partial^2 \Phi_\mathrm{MN}}{\partial z^2} = 4\pi G \rho_\mathrm{MN} (R, z) \tag{41}\]\(\alpha = (z^2 + b^2)^{1/2}, \beta = R^2 + (a+\alpha)^2\)と置くと
\[\frac{\partial \beta}{\partial R} = 2R, \quad \frac{\partial \beta}{\partial z} = 2 (a + \alpha) \frac{\partial \alpha}{\partial z}, \quad \frac{\partial \alpha}{\partial z} = z \alpha^{-1} \tag{42}\]より
\[\frac{\partial \Phi_\mathrm{MN}}{\partial R} = GM R \beta^{-3/2} \tag{43}\] \[\frac{1}{R} \frac{\partial }{\partial R} \left( R \frac{\partial \Phi_\mathrm{MN}}{\partial R}\right) = \frac{GM}{R} \left\{ 2R \beta^{-3/2} + R^2 \left( - \frac{3}{2} \right) \beta^{-5/2} 2R\right\} = GM \beta^{-5/2} (2\beta - 3 R^2) \tag{44}\] \[\frac{\partial \Phi_\mathrm{MN}}{\partial z} = -GM \left( - \frac{1}{2}\right) \beta^{-3/2} 2 (a + \alpha) z \alpha^{-1} = GM z \beta^{-3/2} (1 + a \alpha^{-1}) \tag{45}\] \[\begin{align} \frac{\partial^2 \Phi_\mathrm{MN}}{\partial z^2} &= GM \left\{ \beta^{-3/2} (1+a \alpha^{-1}) + z \left( - \frac{3}{2} \right) \beta^{-5/2} 2 (a + \alpha) z\alpha^{-1} (1+a \alpha^{-1}) + z \beta^{-3/2} a (-1) \alpha^{-2} z \alpha^{-1} \right\} \notag \\ &=GM \beta^{-5/2} \{ \beta (1+a \alpha^{-1}) -3 z^2 (1+a\alpha^{-1})^2 - a z^2 \beta \alpha^{-3}\} \tag{46} \end{align}\]以上より
\[\begin{align} \nabla^2 \Phi_\mathrm{MN} &= GM \beta^{-5/2} \left\{ 2 \beta - 3R^2 + \beta (1+a \alpha^{-1}) -3 z^2 (1+a\alpha^{-1})^2 - a z^2 \beta \alpha^{-3}\right\} \notag \\ &= GM \beta^{-5/2} \alpha^{-3} \left\{ 3 \beta \alpha^3 - 3R^2 \alpha^3 + a \beta \alpha^2 - 3z^2 \alpha^3 (1 + a \alpha^{-1})^2 - az^2 \beta \right\} \tag{47} \end{align}\]式が長いため、中括弧の中身だけ整理していきましょう。
\[\begin{align} \{\cdots \} &= 3 (R^2 + a^2 + 2a \alpha + \alpha^2) \alpha^3 - 3R^2 \alpha^3 + a (R^2 + a^2 + 2a \alpha + \alpha^2) \alpha^2 \notag \\ & \qquad - 3z^2 \alpha^3 (1 + 2a \alpha^{-1} + \alpha^{-2}) - az^2 (R^2 + a^2 + 2a \alpha + \alpha^2) \notag \\ &= 3 \alpha^5 + 7a \alpha^4 + 5a^2 \alpha^3 -3z^2 \alpha^3 + a R^2 \alpha^2 + a^3 \alpha^2 - 7az^2 \alpha^2 - 5a^2 z^2 \alpha - az^2 R^2 - a^3 z^2 \notag \\ &\underbrace{=}_{\alpha^2 = z^2 + b^2} 3 (z^2 + b^2) \alpha^3 + 7a(z^2 + b^2) \alpha^2 + 5a^2 (z^2 + b^2) \alpha - 3 z^2 \alpha^3 + aR^2 (z^2 + b^2) + a^3 (z^2 + b^2) \notag \\ & \qquad \qquad - 7a z^2 \alpha^2 - 5 a^2 z^2 \alpha - az^2 R^2 - a^3 z^2 \notag \\ &= 3b^2 \alpha^3 + 7a b^2 \alpha^2 + 5a^2 b^2 \alpha ab^2 R^2 + a^3 b^2 = b^2 (3\alpha^3 + 7a\alpha^2 + 5a^2 \alpha + a^3) + ab^2 R^2 \notag \\ &= b^2 (3\alpha + a) (\alpha + a)^2 + ab^2 R^2 \tag{48} \end{align}\]これより
\[\rho_\mathrm{MN} (R, z) = \left( \frac{b^2 M}{4\pi} \right) \frac{aR^2 + (a + 3\sqrt{z^2 + b^2}) (a + \sqrt{z^2 + b^2})^2}{\{R^2 + (a + \sqrt{z^2 + b^2})^2\}^{5/2} (z^2 + b^2)^{3/2}} \tag{49}\]と求まります。
下図は\(b/a=0.2, 1.0, 5.0\)として(49)式を描画したものです。
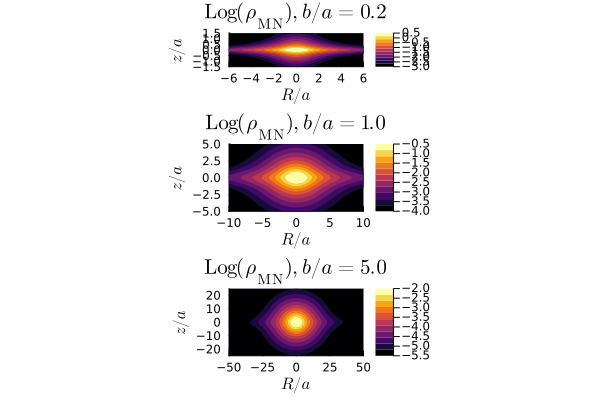(色は適当)
もう一つ、同じような形のポテンシャルとして、Satoh (1980)で提案されたポテンシャルにも触れておきましょう。 これはポアソン方程式が線形であることから、発見された解を足し合わせたものもまた解である、という性質を利用して発見されたものです。 球対称なプラマーモデルのポテンシャルと密度を\(b^2\)で割り、それらの\(b^2\)での\(n\)階微分を計算します。 これらの\(0\sim n\)の総和を求め、最後に\(n \rightarrow \infty\)とすることで、様々な球対称ポテンシャルを足し合わせた形になります。 こうして計算されたポテンシャルと密度は以下のようになります。
\[\Phi_\mathrm{S} (R, z) = - \frac{GM}{S} \qquad (S^2 \equiv R^2 + z^2 + a (a + 2 \sqrt{z^2 + b^2})) \tag{50}\] \[\rho_\mathrm{S} (R, z) = \frac{ab^2M}{4\pi S^3 (z^2 + b^2)} \left\{ \frac{1}{\sqrt{z^2 + b^2}} + \frac{3}{a} \left( 1 - \frac{R^2 + z^2}{S^2}\right) \right\} \tag{51}\]下図は、同じく\(a = 1.0, b=0.2\)として(51)式を描画したものです。 先程の説明の通り、球対称ポテンシャルを足し合わせたものであることから、Miyamoto & Nagai (1975)よりもより楕円体に近い形をしています。
(色は適当)
円盤銀河の回転曲線を再現するモデル: 平らにした対数ポテンシャル
先程の宮本・永井ポテンシャルは円盤銀河をよく再現し、かつ簡潔なモデルです。 しかし、実際の円盤銀河は、バルジ・ディスク・ハローの3つの要素からなります。 よってバルジ・ディスク・ハローを宮本・永井ポテンシャルでそれぞれ再現し、それらを足し合わせることで、より円盤銀河を精密に再現することが可能となります。 すると、パラメータ数が増え、円盤銀河を再現するモデルとしては複雑なものとなります。
パラメータ数が膨大になれば、もちろん様々な銀河を再現することが可能になるでしょう。 しかし、それは簡潔なモデル化とはかけ離れたものになり、そのポテンシャルの物理的な描像が曖昧になります。 そこで以下では、円盤銀河の回転曲線、flat rotationを再現する簡潔なモデルを見ていきましょう。
球対称ポテンシャルのべき乗則ポテンシャルの部分で、flat rotationを再現するポテンシャルは
のように表現されるのでした。 ここで\(v_0\)は回転速度を表す正の実数、\(r = \sqrt{R^2 + z^2}\)は銀河の中心からの距離を表します。 (52)式において
\[r^2 = R^2 + z^2 \ \longrightarrow m^2 = R^2 + \frac{z^2}{q^2} \tag{53}\]のように置き換えることにしましょう。 ここで\(q\)はフラットニングパラメータと呼ばれるものです。 このパラメータにより、球対称なポテンシャルを、楕円体のような潰れた形に変換することが可能となります。 最終的なポテンシャルは
\[\Phi_\mathrm{L} (R, z) = \frac{1}{2} v_0^2 \ln \left( R_c^2 + R^2 + \frac{z_c^2}{q^2}\right) \tag{54}\]のようになります。 ここで新しく登場した\(R_c\)は、\(R = z=0\)でポテンシャルが発散しないためのパラメータです。 このポテンシャルにおける、\(z=0\)での回転速度は
\[\frac{v_c^2}{R} = \frac{\partial \Phi_\mathrm{L}}{\partial R} = \frac{v_0^2 R}{\sqrt{R_c^2 + R^2}} \ \Longrightarrow \ v_c = v_0 \frac{R}{\sqrt{R_c^2 + R^2}} \tag{55}\]と求められます。 (55)式の分数部分は\(R \gg R_c\)で1に漸近します。 よって\(v_c = v_0\)(一定)となることがわかります。 また、この対数ポテンシャルに対応する質量密度分布を求めてみましょう。
\[\begin{align} \nabla^2 \Phi_\mathrm{L} &= \frac{1}{R} \frac{\partial}{\partial R} \left( R \frac{\partial \Phi_\mathrm{L}}{\partial R}\right) + \frac{\partial^2 \Phi_\mathrm{L}}{\partial z^2} = v_0^2 \frac{2 \left( R_c^2 + \frac{z^2}{q^2}\right)}{\left( R_c^2 + R^2 + \frac{z^2}{q^2}\right)^2} + v_0^2 \frac{\frac{1}{q^2} \left(R_c^2 + R^2 + \frac{z^2}{q^2}\right) - \frac{2z^2}{q^4}}{\left( R_c^2 + R^2 + \frac{z^2}{q^2}\right)^2} \notag \\ &= \frac{v_0^2}{q^2} \frac{(2q^2 + 1) R_c^2 + R^2 + \left( 2-\frac{1}{q^2} \right) z^2}{ \left( R_c^2 + R^2 + \frac{z^2}{q^2} \right)^2} \tag{56} \end{align}\]以上より
\[\rho_\mathrm{L} (R, z) = \frac{v_0^2}{4\pi G q^2} \frac{(2q^2 + 1) R_c^2 + R^2 + \left( 2-\frac{1}{q^2} \right) z^2}{ \left( R_c^2 + R^2 + \frac{z^2}{q^2} \right)^2 } \tag{57}\]を得ます。 下図は\(q = 0.95, 0.7\)の場合を図示したものです。
(色は適当)
\(R, z \ll 1\)の場合、\(\rho_\mathrm{L}\)は一定の値になります。 \(R \gg 1\)の場合、\(\rho_\mathrm{L} \propto R^{-2}\)となり、\(z \gg 1\)の場合には、\(\rho_\mathrm{L} \propto z^{-2}\)となります。 (57)式にマイナスの符号を持つ項が存在することから分かるように、パラメータ選択によっては、この密度分布は負の値となる領域が存在することがわかります。
この密度分布は楕円体とはほど遠いものですが、仮に\(R, z \gg R_c\)の場合に\(\rho_\mathrm{L} = C\)となるような等高線が、楕円であると近似しましょう。 \(\rho_\mathrm{L}(R, 0) = \rho_\mathrm{L}(0, z)\)となる\(z/R\)を楕円の軸比\(q_\rho\)と定義すると
となります。 この結果から分かるように、\(q < 1/\sqrt{2}\)の場合には\(q_\rho\)が負になります。 これは\(\rho_\mathrm{L}\)が負になる領域の存在を示しています。
余談: 天の川銀河を再現するには？（工事中…近いうちに図を掲載予定）
ここまで、様々な軸対称ポテンシャルをご覧いただきました。 ではこれらを用いて、私たちの住まう天の川銀河の重力ポテンシャル(もしくはそこから求められる回転曲線)を再現することを考えましょう。 簡単のため、天の川銀河中心に存在する棒状構造は考えないとします。 すると、円盤銀河はバルジ・ディスク・ハローの3成分からなると考えることができます。
Guo & Mathews (2012)の場合
Guo & Mathews (2012)は、天の川銀河中心から放出されたAGNジェットの進化を、宇宙線を考慮した流体力学方程式を解くことで解明した研究です。 中心部から注入された宇宙線を伴う高速流が起こす衝撃波と空洞が、天の川銀河ハロー部分にまで広がっていく様子が、シミュレーションから得られました。
この論文で用いられている天の川銀河の重力ポテンシャルは、以下のようなものです。
ここで\(r = \sqrt{R^2 + z^2}\)は銀河中心からの距離、\(v_\mathrm{halo}=131.5 \mathrm{km \ s^{-1}}, d_\mathrm{h} = 12 \mathrm{kpc}, M_\mathrm{disk} = 10^{11} M_\odot, a = 6.5 \mathrm{kpc}, b = 0.26 \mathrm{kpc}, M_\mathrm{bulge} = 3.4 \times 10^{10} M_\odot, d_\mathrm{b} = 0.7 \mathrm{kpc}\)などです。 (59)式は球対称のべき乗則モデルで紹介した、銀河のflat rotationを再現するポテンシャルです。 {60}式は宮本・永井ポテンシャルで円盤を表現したもの、そして(61)式は球対称のハーンキストモデルです。 バルジとハローには球対称モデルを用意し、円盤部分は軸対称モデルを用いています。
Nishikori et al. (2006)の場合
Nishikori et al. (2006)は、円盤銀河中の磁気流体シミュレーションを行なったものです。 初期に用意された弱い方位角磁場が、磁気回転不安定性により増幅され、それがパーカー不安定性によりハローへと逃走する物理過程を示しました。 この論文で用いられた銀河のポテンシャルは、以下のようなシンプルなものです。
\[\Phi = - \sum_{i=1}^3 \frac{GM_i}{\sqrt{R^2 + (a_i + \sqrt{z^2 + b_i^2})^2}} \tag{62}\]ここで\(i=1, 2, 3\)はそれぞれバルジ・ディスク・ハローに対応しています。 また用いたパラメータは\(a_1 = 0.0\mathrm{kpc}, b_1 = 0.47\mathrm{kpc}, M_1 = 1.95 \times 10^{10} M_\odot, a_2 = 6.2 \mathrm{kpc}, b_2 = 0.15 \mathrm{kpc}, M_2 = 1.74 \times 10^{11} M_\odot, a_3 = 0.0 \mathrm{kpc}, b_3 = 31.2 \mathrm{kpc}, M_3 = 7.35 \times 10^{11} M_\odot\)です。
Kakiuchi et al. (2024)の場合
Kakiuchi et al. (2024)は、銀河中心領域の磁気流体シミュレーションを行なったものです。 放射冷却と加熱を考慮することで、銀河中心部に磁場が卓越した領域が発生することを示しました。 この論文で用いられた銀河のポテンシャルは、上述の2つとは異なり、銀河中心の超大質量ブラックホールを考慮したものになっています。
\[\Phi_\mathrm{SMBH} = - \frac{GM_\mathrm{SMBH}}{r} \tag{63}\] \[\Phi_\ast = - \sum_{i=1}^2 \frac{GM_i}{\sqrt{R^2 + (a_i + \sqrt{z^2 + b_i^2})^2}} \tag{64}\] \[\Phi_\mathrm{halo} = - 4\pi G \rho_{h, 0} r_h^3 \frac{1+ r/r_h}{r} \tag{65}\]ここで\(M_\mathrm{SMBH}=4.4 \times 10^6 M_\odot, M_1 = 2.05 \times 10^{10} M_\odot, M_2 = 2.57 \times 10^{11} M_\odot, a_1 = 0.0 \mathrm{kpc}, a_2 = 7.258 \mathrm{kpc}, b_1 = 0.495 \mathrm{kpc}, b_2 = 0.52 \mathrm{kpc}, r_h = 10.2 \mathrm{kpc}, \rho_{h, 0} = 1.82 \times 10^{-2} M_\odot \mathrm{pc}^{-3}\)です。 (63)式は銀河中心に存在する超大質量ブラックホールが作る重力ポテンシャルです。 (64)式は\(i=1\)がバルジ、\(i=2\)がディスクを表しています。 (65)式はダークハローを表し、ここではNFWモデルを採用しています。
参考文献
[1] Binney & Tremaine, “Galactic Dynamics: Second Edition”
[2] Bovy, “Dyanmics and Astrophysics of Galxies”
[3] Miyamoto & Nagai, 1975, “Three-dimensional models for the distribution of mass in galaxies”
[4] Satoh, 1980, “Dynamical Models of Axisymmetric Galaxies and Their Applications to the Elliptical Galaxy NGC4697”
[5] Guo & Mathews, 2012, “The Fermi Bubbles. I. Possible Evidence for Recent AGN Jet Activity in the Galaxy”
[6] Nishikori et al., 2006, “Global Three-dimensional Magnetohydrodynamic Simulations of Galactic Gaseous Disks. I. Amplification of Mean Magnetic Fields in an Axisymmetric Gravitational Potential”
[7] Kakiuchi et al., 2024, “MHD Simulation in Galactic Center Region with Radiative Cooling and Heating”