2.4 Schwarzschild-Milne Equations

Mean intensity \(J_\nu\)の定義式(2.12)に深さ無限大のPlane-parallel atmosphereに対するformal solution (2.19), (2.20)式を用いると

\[J_\nu (\tau_\nu) = \frac{1}{2} \left\{ \int_0^1 d\mu \int_{\tau_\nu}^\infty S_\nu (t) e^{-\frac{t-\tau_\nu}{\mu}} \frac{dt}{\mu} + \int_{-1}^0 d\mu \int_{0}^{\tau_\nu} S_\nu (t) e^{-\frac{t-\tau_\nu}{-\mu}} \frac{dt}{-\mu} \right\} \tag{2.36}\]

のように表されます。\(\mu, t\)の積分順序を交換し、\(w = \pm 1/\mu\)という変数変換を行うと

\[\begin{align} J_\nu (\tau_\nu) &= \frac{1}{2} \left\{ \int_{\tau_\nu}^\infty dt S_\nu (t) \int_1^\infty e^{-w (t-\tau_\nu) \frac{dw}{w}} + \int_0^{\tau_\nu} S_\nu (t) \int_1^\infty e^{-w(\tau_\nu -t)} \frac{dw}{w} \right\} \notag \\ &= \frac{1}{2} \int_0^\infty dt S_\nu (t) \int_1^\infty e^{-w|t-\tau_\nu|} w^{-1} dw \tag{2.37} \end{align}\]

のように変形されます。\(w\)についての積分の部分は、第1 Exponential integralと呼ばれる積分です。その一般形は

\[E_n (x) \equiv \int_1^\infty t^{-n} e^{-xt} dt = x^{n-1} \int_x^\infty t^{-n} e^{-t} dt \tag{2.38}\]

のように表されます。\(E_1\)を用いると、(2.37)式は

\[J_\nu (\tau_\nu) = \frac{1}{2} \int_0^\infty S_\nu (t) E_1(|t-\tau_\nu|) dt \tag{2.39}\]

のように表現されます。この式はK. Schwarzschild によって最初に導出されました。Source function \(S_\nu\)に(2.14)式を用いると、上式は

\[J_\nu (\tau_\nu) - \frac{1}{2} \int_0^\infty \frac{\sigma_\nu}{\kappa_\nu + \sigma_\nu} J_\nu (t) E_1(|t-\tau_\nu|) dt = \frac{1}{2} \int_0^\infty \frac{\kappa_\nu}{\kappa_\nu + \sigma_\nu} B_\nu (t) E_1(|t-\tau_\nu|) dt\]

のように表されます。これは散乱\(\sigma_\nu\)が無視できないときは、\(J_\nu (\tau_\nu)\)を得るためには積分方程式を解く必要があることを示しています。

同様にして\(F_\nu (\tau_\nu), K_\nu (\tau_\nu)\)を求めてみましょう。

\[\begin{aligned} F_\nu (\tau_\nu) &= \int_{4\pi} \mu I_\nu (\theta, \tau_\nu) d\Omega = 2\pi \left( \int_0^1 \mu I^+ d\mu + \int_{-1}^0 \mu I^- d\mu \right) \\ &= 2\pi \left\{ \int_0^1 d\mu \mu \int_{\tau_\nu}^\infty dt \frac{S_\nu (t)}{\mu} e^{-\frac{t-\tau_\nu}{\mu}} + \int_{-1}^0 d\mu \mu \int_0^{\tau_\nu} dt \frac{S_\nu (t)}{-\mu} e^{-\frac{\tau_\nu-t}{-\mu}}\right\} \\ &= 2\pi \left\{ \int_{\tau_\nu}^\infty dt S_\nu (t) \int_0^1 d\mu e^{-\frac{t-\tau_\nu}{\mu}} + \int_0^{\tau_\nu} dt S_\nu (t) \int_{-1}^0 d\mu e^{-\frac{\tau_\nu-t}{-\mu}} (-1) \right\} \end{aligned}\]

\(w = 1/\mu\)とおくと\(d\mu = -dw/w^2\)より

\[\int_0^1 d\mu e^{-\frac{t-\tau_\nu}{\mu}} = \int_\infty^1 dw \left( -\frac{1}{w^2} \right) e^{-(t-\tau_\nu)w} = \int_1^\infty dw \frac{e^{-(t-\tau_\nu)w}}{w^2}\]

同様に\(w = -1/\mu\)とおくと\(d\mu = dw/w^2\)より

\[\int_{-1}^0 d\mu e^{-\frac{\tau_\nu-t}{-\mu}} (-1) = \int_1^\infty dw \frac{1}{w^2} e^{-(\tau_\nu-t)w} (-1)\]

第1 Exponential integral (2.38)を用いると

\[F_\nu (\tau_\nu) = 2\pi \left\{ \int_{\tau_\nu}^\infty dt S_\nu (t) E_2 (t-\tau_\nu) - \int_0^{\tau_\nu} dt S_\nu (t) E_2 (\tau_\nu - t) \right\} \tag{2.40}\]

同じようにして、\(K_\nu (\tau_\nu)\)を求めてみましょう。

\[\begin{aligned} K_\nu (\tau_\nu) &= \frac{1}{4\pi} \int_{4\pi} \mu^2 I_\nu (\theta, \tau_\nu) d\Omega = \frac{1}{2} \left( \int_0^1 d\mu \mu^2 I_\nu^+ + \int_{-1}^0 d\mu \mu^2 I_\nu^- \right) \\ &= \frac{1}{2} \left\{ \int_0^1 d\mu \mu^2 \int_{\tau_\nu}^\infty dt \frac{S_\nu (t)}{\mu} e^{-\frac{t-\tau_\nu}{\mu}} + \int_{-1}^0 d\mu \mu^2 \int_0^{\tau_\nu} dt \frac{S_\nu (t)}{-\mu} e^{-\frac{\tau_\nu-t}{-\mu}}\right\} \\ &= \frac{1}{2} \left\{ \int_{\tau_\nu}^\infty dt S_\nu (t) \int_0^1 d\mu \mu e^{-\frac{t-\tau_\nu}{\mu}} + \int_0^{\tau_\nu} dt S_\nu (t) \int_{-1}^0 d\mu \mu e^{-\frac{\tau_\nu-t}{-\mu}} (-1) \right\} \end{aligned}\]

\(F_\nu(\tau_\nu)\)を求めるときと同様に\(w=\pm 1/\mu\)の変数変換を施して

\[K_\nu (\tau_\nu) = \frac{1}{2} \left\{ \int_{\tau_\nu}^\infty dt S_\nu (t) \int_1^\infty dw \frac{e^{-(t-\tau_\nu)w}}{w^3} + \int_0^{\tau_\nu} dt S_\nu (t) \int_1^\infty dw \frac{e^{-(\tau_\nu-t)w}}{w^3}\right\}\]

ここで

\[\int_0^\infty dt S_\nu (t) e^{-|t-\tau_\nu| w} = \int_0^{\tau_\nu} dt S_\nu (t) e^{-(\tau_\nu -t)w} + \int_{\tau_\nu}^\infty dt S_\nu (t) e^{-(t-\tau_\nu)w}\]

より

\[K_\nu (\tau_\nu) = \frac{1}{2} \int_0^\infty dt S_\nu (t) \int_1^\infty dw \frac{e^{-|t-\tau_\nu| w}}{w^3} = \frac{1}{2} \int_0^\infty dt S_\nu (t) E_3 (|t-\tau_\nu|) \tag{2.41}\]

(2.40), (2.41)式はMilneによって導出されました。

Appendix: Exponential Integral

漸化式

Exponential Integralが満たす漸化式を導出しましょう。

\[\frac{d E_n}{dx} = \int_1^\infty dt t^{-n} \frac{d}{dx} (e^{-xt}) = \int_1^\infty dt t^{-n} (-t) e^{-xt} = - \int_1^\infty dt t^{-(n-1)} e^{-xt} = -E_{n-1} (x) \tag{A.1}\]

\(n>1\)のとき

\[\begin{align} E_n (x) &= \int_1^\infty dt t^{-n} e^{-xt} = \left[ \frac{1}{-n+1} t^{-n+1} e^{-xt} \right]_1^\infty - \int_1^\infty \frac{1}{-n+1} t^{-n+1} (-x) e^{-xt} \notag \\ &= - \left( \frac{1}{-n+1} e^{-x} \right) - \frac{x}{n-1} \int_1^\infty dt t^{-(n-1)} e^{-xt} = \frac{1}{n-1} ( e^{-x} - x E_{n-1} (x) ) \tag{A.2} \end{align}\]

近似式

(A.2)式より

\[n E_{n+1} (x) = e^{-x} - x E_n (x) \ \Longrightarrow \ E_n(x) = \frac{e^{-x}}{x} -\frac{n}{x} E_{n+1} (x) = \frac{e^{-x}}{x} -\frac{n}{x} \left[ \frac{e^{-x}}{x} - \frac{n+1}{x} E_{n+2}\right] = \cdots\]

よって、\(x \gg 1\)のとき

\[E_n (x) \simeq \frac{e^{-x}}{x} \tag{A.3}\]

となります。

グラフ図示

以下に Exponential Integral を図示したものと、それを計算するPythonスクリプトを示します。

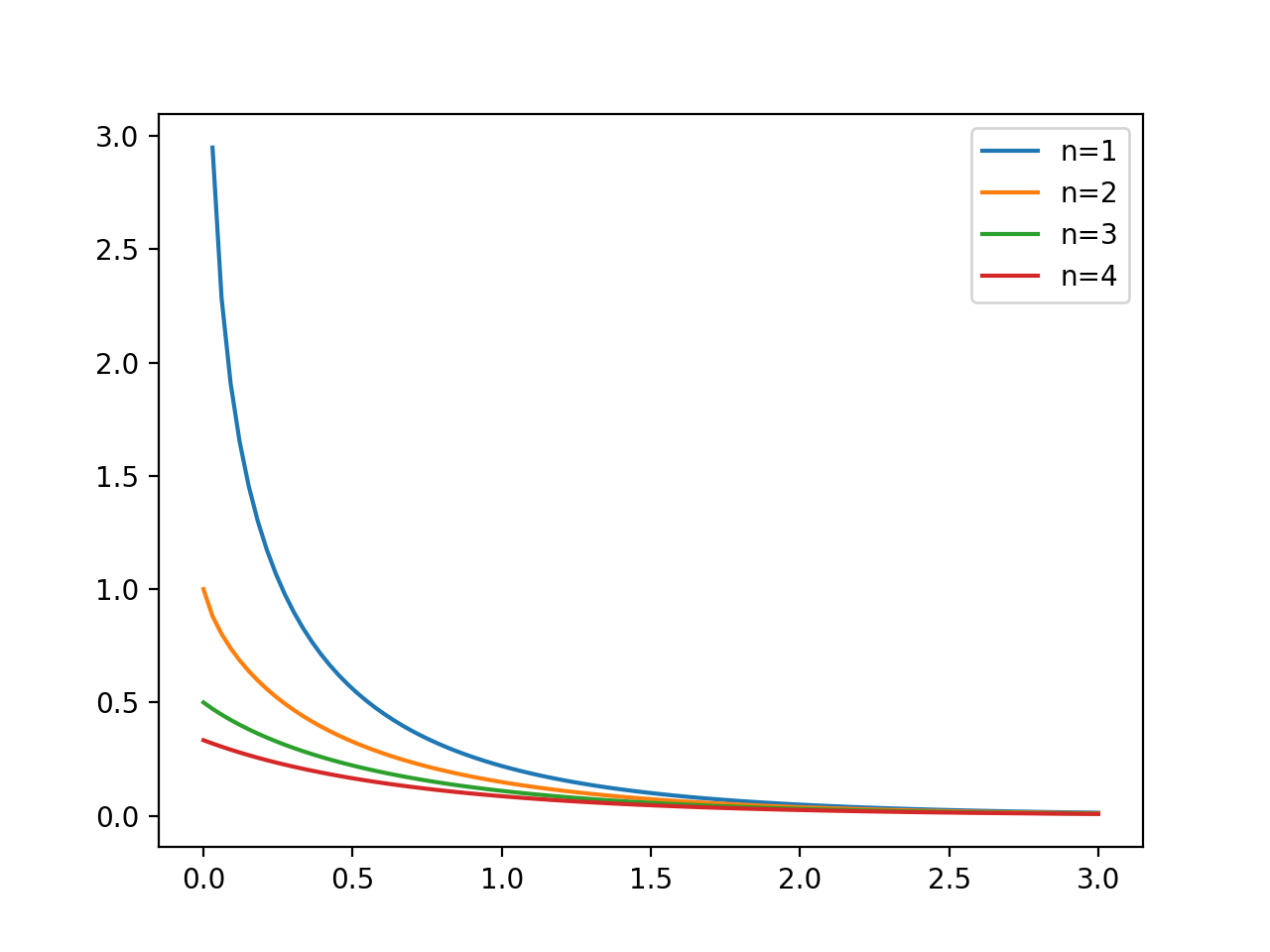
Exponential Integralの例

#!/usr/bin/env python3 

import numpy as np
import matplotlib.pyplot as plt
import scipy.special as sc

if __name__ == '__main__':
    # set variables
    ix = 100
    xmin = 0.0
    xmax = 3.0
    nmin = 1
    nmax = 5
    # set x coordinate
    x = np.linspace(xmin, xmax, ix)
    # main loop of plotting Laguerre polynomial
    for n in range(nmin, nmax):
        ei = sc.expn(n, x)
        string = "n={}".format(n)
        plt.plot(x, ei, label=string)
        plt.legend()
    # make plot window
    plt.show()