Table of contents
境界条件
ここでは、オイラー的な(磁気)流体計算に必要となる境界条件についてメモしています。
境界条件の定め方
その名の通り、計算領域の端に対して定める条件です。通常は、衝撃波などの激しい物理現象が起こるような、十分解像して調べたい領域から十分離れた場所に境界を設置します。 HLL法やHLLD法のような近似リーマン解法の場合、セル中心だけでなく、セルとセルの間の仕切り部分(インターフェース)に対しても境界条件を設定する必要があります。
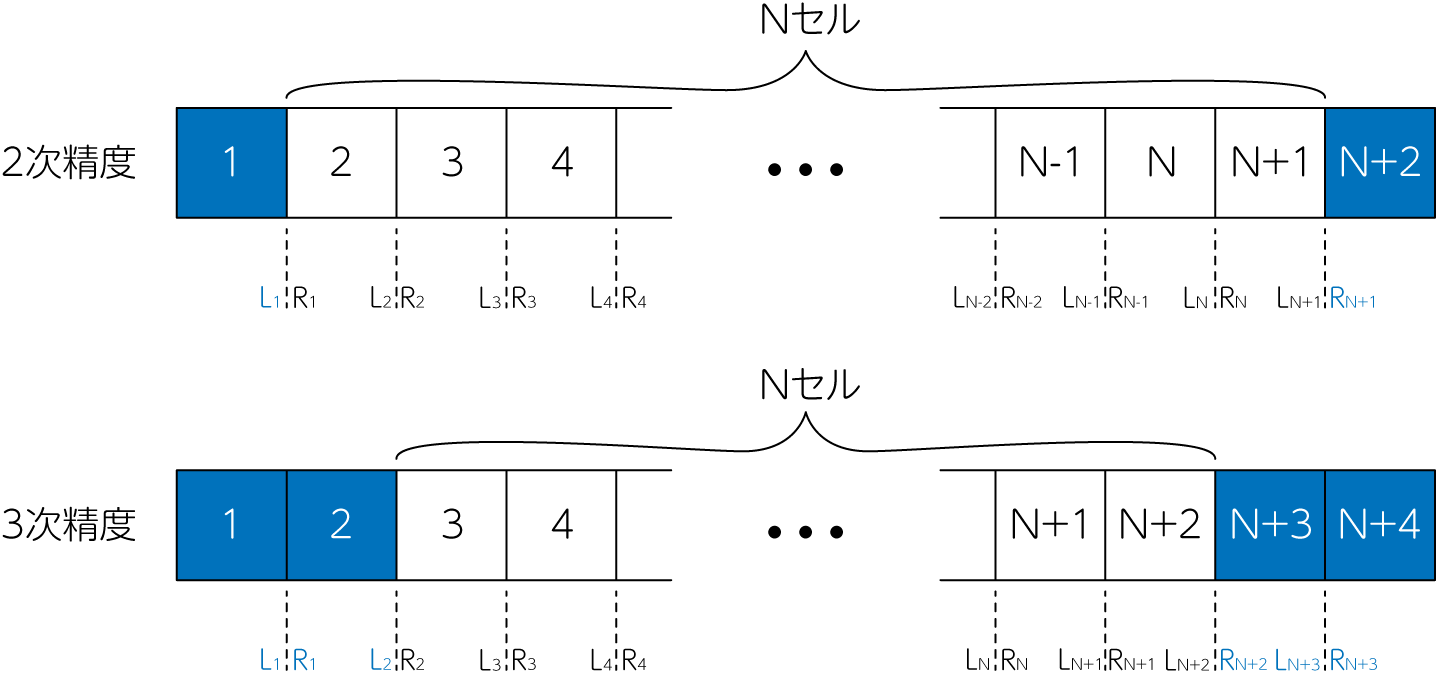
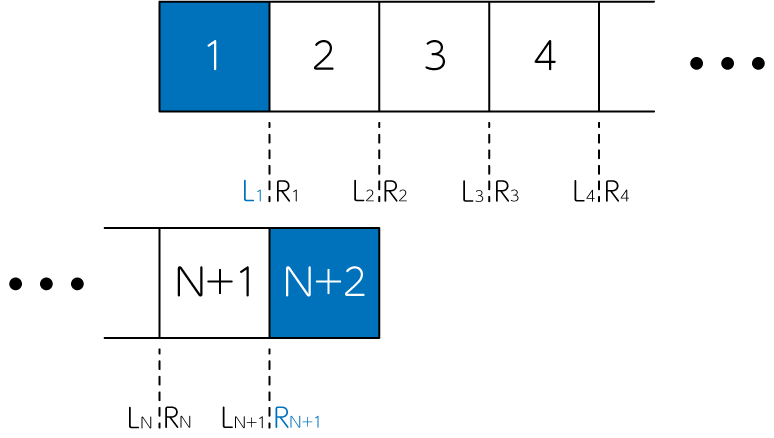
上図のように1次元の流体計算を\(N\)個のセルを用いて数値計算する場合を考えましょう。このとき、\(N\)個のセルの両端に境界条件のための「のりしろ」を準備します。こののりしろのセル数は、ソルバーの精度によって変化します。 例えば2次精度であれば両側に1セルずつ、3次精度であれば両側に2セルずつ用意します。一般に、\(n\)次精度のソルバーで流体計算を行う場合には、\(n-1\)個のセルを計算領域の両側に配置する必要があります。
2次精度の場合、上図から1番目と\(N+2\)番目のセルに境界条件を課します。これは1番目のセルの左側のインターフェースが存在しないため、流速計算を行うことができず、時間発展をさせることができないためです。 同様に、1番目のセルと2番目のセルの間にあるインターフェースにおいて、左側の物理量\(L_1\)も定めることができません。\(R_1\)は2番目と3番目のセルの物理量からの外挿、もしくは1番目と2番目のセルの物理量からの内挿により、求めることができます。 同じ理由から、\(N+1\)番目と\(N+2\)番目のセルの間にあるインターフェースの右側の物理量\(R_{N+1}\)も求めることができないことがわかります。よって2次精度の場合には、1番目と\(N+2\)番目のセル、そして\(L_1, R_{N+1}\)のインターフェース物理量は境界条件から定めます。
3次精度の場合には、1番目と2番目と\(N+3\)番目と\(N+4\)番目のセル、そして\(L_1, R_1, L_2, R_{N+2}, L_{N+3}, R_{N+3}\)のインターフェース物理量を境界条件から定める必要があります。
様々な境界条件
それでは実際に、どのような境界条件が存在するかを見てみましょう。以下では簡単のため、計算精度は2次精度であるとします。先程の議論から計算領域に\(N\)セルを準備した場合、1セル目と\(N+2\)セル目は境界に用いるのりしろ、そして\(2 \leq i \leq N+1\)セル目が実際に計算を行う領域です。
自由端境界
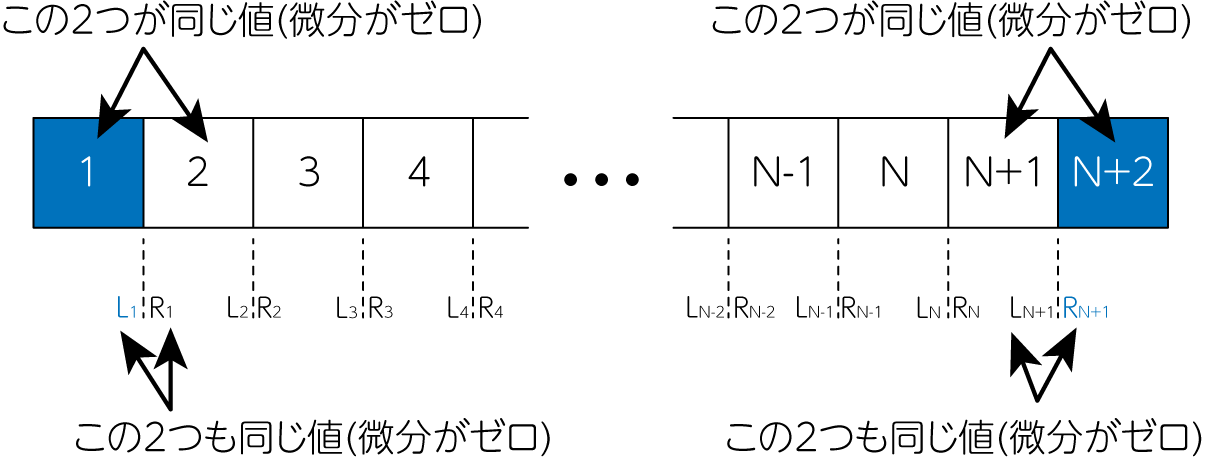
\(i\)番目のセルの\(n\)計算ステップ目の物理量を\(\mathbf{U}_i^n\)のように書きましょう。自由端境界では微分がゼロになるように物理量を定める必要があるため、以下のように課します。
\[\mathbf{U}_{1}^{n} = \mathbf{U}_{2}^n, \quad \mathbf{U}_{N+2}^{n} = \mathbf{U}_{N+1}^n\tag{1}\]さらにインターフェースの左側・右側の物理量をそれぞれ\(\mathbf{U}_{L, i}^n, \mathbf{U}_{R, i}^n\)のように書くと、インターフェースに対しては
\[\mathbf{U}_{L, 1}^n = \mathbf{U}_{R, 1}^n, \quad \mathbf{U}_{R, N+1}^n = \mathbf{U}_{L, N+1}^n \tag{2}\]とすることで微分がゼロとなります。
実際に数値計算した場合の挙動を以下に示します。
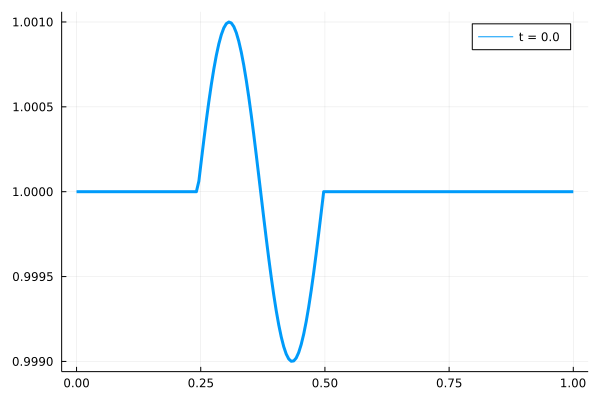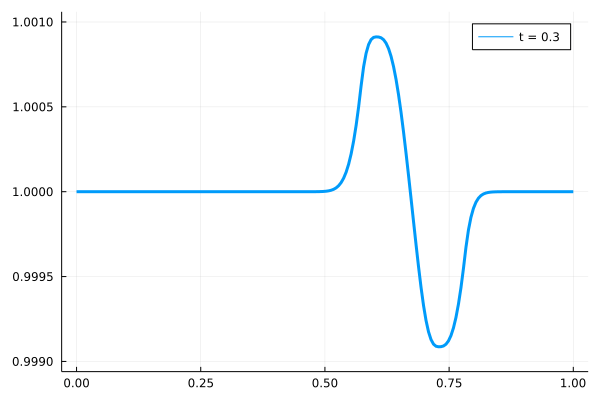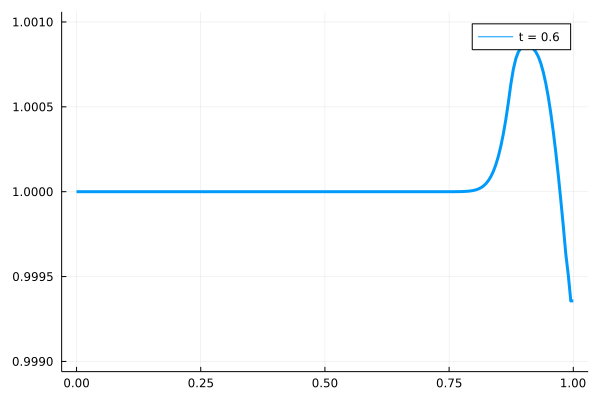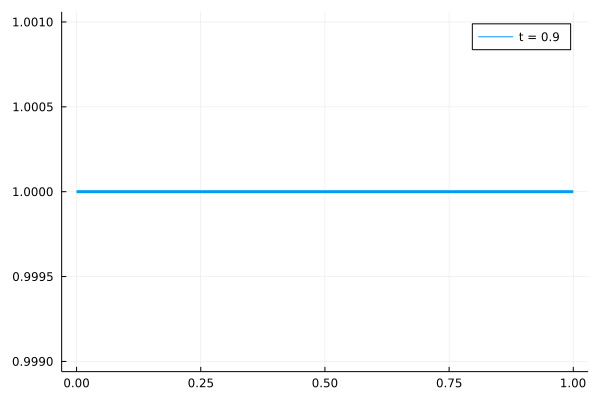
微小振幅の波形が自由端境界条件を課した領域に到達すると、その波形は計算領域からさらに右側に流出していきます。
用いたソルバーの精度などの特徴から、数値的な粘性により波形のピークが減衰しています。ご了承ください。
周期境界
続いて周期境界です。左側の端からさらに左に進むと、右側の端に到達するのが周期境界の考え方です。
わかりやすい(?)例えとして、ドラクエやファイナルファンタジーのマップ移動が考えられます。
上にずっと進んでいき上端に到達すると、今度はマップの下端から出てくるという構造です。
この周期境界を数式で表しましょう。セル中の物理量に対しては以下のように定めることができます。
\[\mathbf{U}_{1}^n = \mathbf{U}_{N+1}^n, \quad \mathbf{U}_{N+2}^n = \mathbf{U}_2^n \tag{3}\]さらにインターフェース上の物理量に対しては
\[\mathbf{U}_{L, 1}^n = \mathbf{U}_{L, N+1}^n, \quad \mathbf{U}_{R, N+1} = \mathbf{U}_{R, 1} \tag{4}\]のようになります。このようにすることで、セルだけでなく、インターフェースも一致する周期境界を課すことができます。
実際に周期境界条件をテストした結果を、以下に示します。
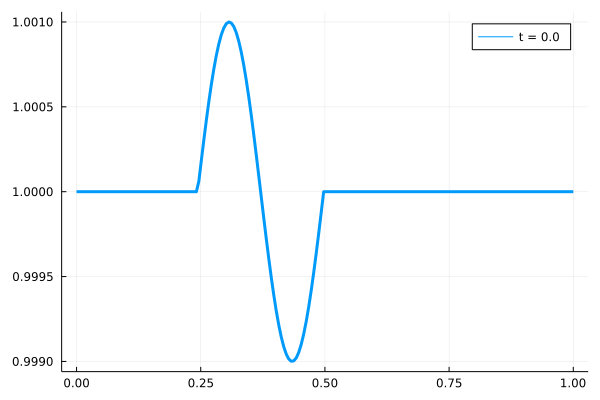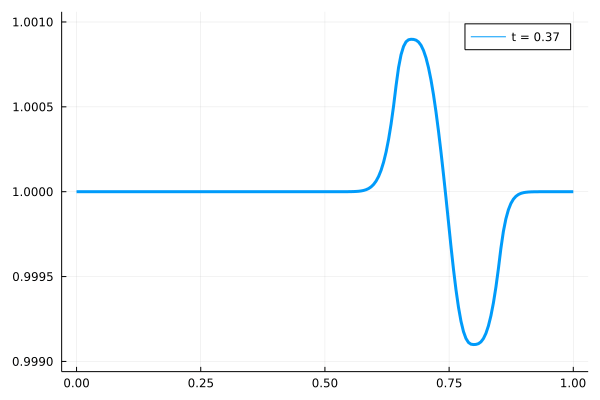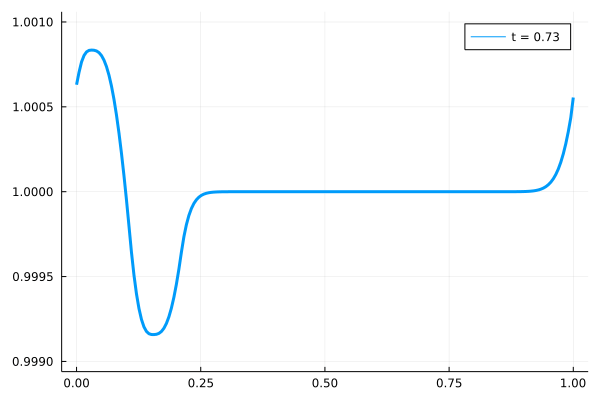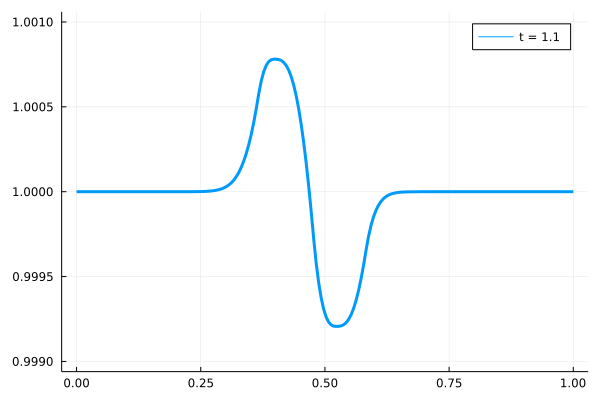
右端に到達した波形が、左端から再び移動してくる様子が計算されています。
減衰境界
計算領域内で発生したある波動が境界に到達すると、その境界で反射する場合があります。境界部分で反射された波動が再び計算領域を横断することで、計算結果を大きく変化させるようなことは防がなければいけません。 境界に到達した波動を減衰させることで、これを回避するような境界条件を定めましょう。それには以下のように考えます。
\[{\mathbf{U}'}_i^n = \mathbf{U}_i^n - D(x) (\mathbf{U}_i^n - \mathbf{U}_i^0) \quad (i \in 境界領域) \tag{5}\]ここで\(D\)は減衰係数、そして\(\mathbf{U}_i^0\)は初期条件により定められた物理量の値です。\(D\)は\(0 \leq D \leq 1\)となるように定義します。 もし\(D = 0\)ならば、境界条件を課した後の物理量の値\(\mathbf{U}'\)は、境界条件を課さない場合である\(\mathbf{U}\)に一致します。 逆に\(D = 1\)ならば、\(\mathbf{U}' = \mathbf{U}^0\)となり、初期条件の値となります。
境界に到達した波動の振幅を突然ゼロにすると、固定端のように波動が反射することが考えられます。よって徐々に振幅をゼロにさせるように、この減衰係数を定めます。 この定め方の一つに以下のようなものがあります。
ここで\(x\)は計算領域の座標、\(\Delta x\)は計算領域を分割するセル幅、\(A, a\)は適当な実数です。 ここで\(a, x\)ともに正の値であるとしましょう。\(x < a\)であれば\(0 < \tanh (\cdots )< 1\)となります。極端に\(\tanh (\cdots) \rightarrow 1\)の場合を考えると、\(D(x) \rightarrow 0\)となり、これは減衰がない状態に一致します。 しかし\(x > a\)であれば\(-1 < \tanh (\cdots )< 0\)となります。極端に\(\tanh (\cdots) \rightarrow -1\)の場合を考えると、\(D(x) \rightarrow 2A\)となり、これは減衰された状態を表します。
実際に計算領域を\(0 \leq x \leq 1\)、計算領域のセル数を\(N = 200\)とし、さらに\(A = 0.05, a = 0.75\)として計算した場合の計算結果を以下に示します。
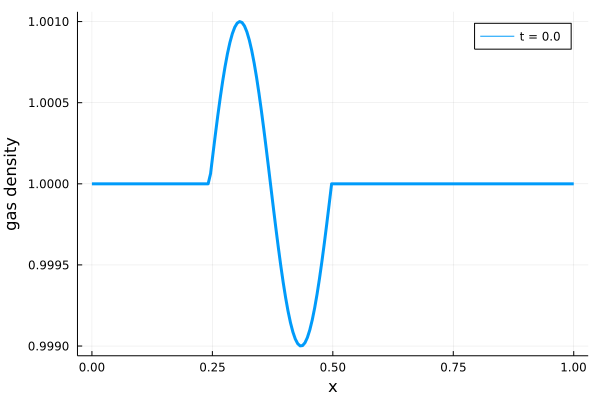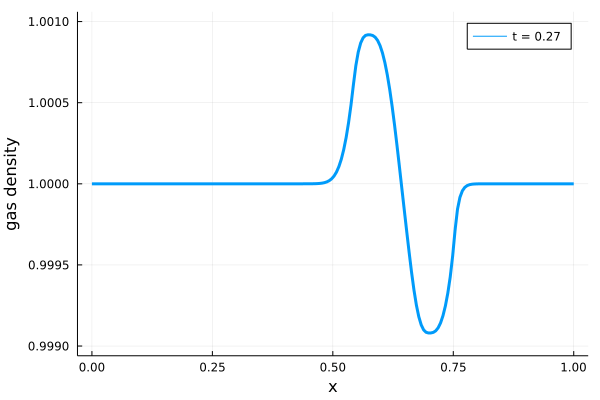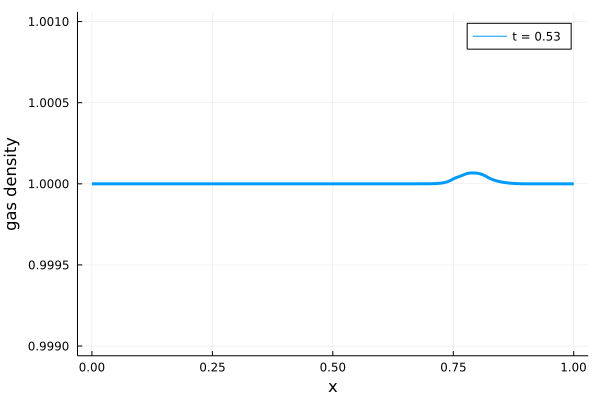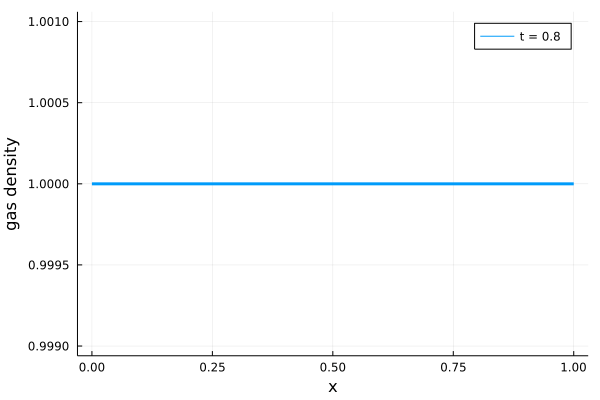
\(x = 0.75\)に到達した波形が減衰を受けていることがわかります。様々な波動に対して\(A, a\)などを変化させ、振る舞いがどのように変わるか(反射が起こるかどうか)を確認すると面白いかもしれません。
軸境界(工事中)
対称境界(工事中)
反対称境界(工事中)
シアリングボックス境界(工事中)
参考文献
- Nishikori et al., 2006, “Global Three-dimensional Magentohydrodynamic Simulations of Galactic Gaseous Disks. I. Amplification of Mean Magnetic Fields in an Axisymmetric Gravitational Potential”
- Kudoh et al., 2020, “Multiphase Circumnuclear Gas in a Low-β Disk: Turbulence and Magnetic Field Reversals”