Table of contents
等温の場合のHLLD
磁気流体方程式群
宇宙空間に存在するガスは圧縮を受けると一時的に高温になりますが、放射冷却などの他の物理過程により素早くエネルギーを失う場合には、圧縮の前後で等温の状態が保たれる場合があります。 そのような場合には、エネルギーの方程式を考える必要がなく、1次元の理想磁気流体方程式は以下のようになります。
\[\frac{\partial}{\partial t}\left( \begin{array}{c} \rho \\ \rho v_x \\ \rho v_y \\ \rho v_z \\ B_y \\ B_z \end{array} \right) + \frac{\partial}{\partial x} \left( \begin{array}{c} \rho v_x \\ \rho v_x v_x + P_\mathrm{tot} - B_x B_x \\ \rho v_y v_x - B_y B_x \\ \rho v_z v_x - B_z B_x \\ B_y v_x - B_x v_y \\ B_z v_x - B_x v_z \end{array} \right) = \mathbf{0} \tag{1}\]このとき、HLLD法はどのように変形されるでしょうか。それを見てみましょう。以降では普通のHLLDを断熱HLLD、等温の場合を等温HLLDと呼ぶことにします。
流束計算
(1)式の特性速度を計算すると、実は以下の6つになります。
\[\lambda_{1, 6} = v_x \pm c_f, \quad \lambda_{2, 5} = v_x \pm c_a, \quad \lambda_{3, 4} = v_x \pm c_s \tag{2}\]ここで\(c_f, c_a, c_s\)はそれぞれ速い磁気音波の伝播速度、アルヴェーン速度、遅い磁気音波の伝播速度です。 断熱HLLDでは、ここにさらに\(\lambda = v_x\)で伝播するエントロピー波が存在します。今は等温を考えているため、エントロピー波のようにその波面を挟んで温度の不連続が発生することはありません。
よって断熱HLLDのときと同様に遅い磁気音波は無視することに加え、エントロピー波を考慮しない以下のようなリーマンファンを考えます。
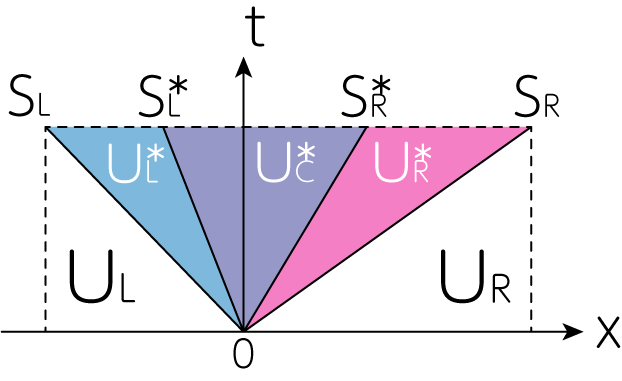
ここで\(S_L, S_R\)はそれぞれ左方向と右方向に進む速進磁気音波の波面、\(S_L^\ast, S_R^\ast\)はそれぞれ左方向と右方向に進むアルヴェーン波の波面です。断熱HLLDでは中間状態において\(x\)方向の流体速度と全圧力を一定としました。よって等温HLLDでも同様に
\[v^\ast_{x, L} = v^\ast_{x, c} = v^\ast_{x, R} \equiv v_x^\ast \tag{3}\] \[P^\ast_{\mathrm{tot}, L} = P^\ast_{\mathrm{tot}, c} = P^\ast_{\mathrm{tot}, R} \equiv P^\ast_{\mathrm{tot}} \tag{4}\]を仮定します。さらに断熱HLLDの(19)式から\(\rho_L^{\ast \ast} = \rho_L^\ast, \rho_R^{\ast \ast} = \rho_R^\ast\)でしたが、今は\(\mathbf{U}_L^{\ast \ast}, \mathbf{U}_R^{\ast \ast}\)の状態は\(\mathbf{U}_c^\ast\)という状態に集約されているため
\[\rho_L^\ast = \rho_c^\ast = \rho_R^\ast \equiv \rho^\ast \tag{5}\]が成り立ちます。これらを踏まえた上で、\(S_\alpha\)の波面でのジャンプ条件を見ていきましょう。
\[S_\alpha \left( \begin{array}{c} \rho^\ast \\ \rho^\ast v_x^\ast \\ \rho^\ast v_{y, \alpha}^\ast \\ \rho^\ast v_{z, \alpha}^\ast \\ B_{y, \alpha}^\ast \\ B_{z, \alpha}^\ast \end{array} \right) - \left( \begin{array}{c} \rho^\ast v_x^\ast \\ \rho^\ast v_x^\ast v_x^\ast + P_\mathrm{tot}^\ast - B_x B_x \\ \rho^\ast v_{y, \alpha}^\ast v_x^\ast - B_{y, \alpha}^\ast B_x \\ \rho^\ast v_{z, \alpha}^\ast v_x^\ast - B_{z, \alpha}^\ast B_x \\ B_{y, \alpha}^\ast v_x^\ast - v_{y, \alpha}^\ast B_x \\ B_{z, \alpha}^\ast v_x^\ast - v_{z, \alpha}^\ast B_x \end{array} \right) = S_\alpha \left( \begin{array}{c} \rho_\alpha \\ \rho_\alpha v_{x, \alpha} \\ \rho_\alpha v_{y, \alpha} \\ \rho_\alpha v_{z, \alpha} \\ B_{y, \alpha} \\ B_{z, \alpha} \end{array} \right) - \left( \begin{array}{c} \rho_\alpha v_{x, \alpha} \\ \rho_\alpha v_{x, \alpha} v_{x, \alpha} + P_{\mathrm{tot}, \alpha} - B_x B_x \\ \rho_\alpha v_{y, \alpha} v_{x, \alpha} - B_{y, \alpha} B_x \\ \rho_\alpha v_{z, \alpha} v_{x, \alpha} - B_{z, \alpha} B_x \\ B_{y, \alpha} v_{x, \alpha} - v_{y, \alpha} B_x \\ B_{z, \alpha} v_{x, \alpha} - v_{z, \alpha} B_x \end{array} \right) \tag{6}\]ここで(6)式の第一, 第二式に着目してみましょう。
\[S_\alpha \rho^\ast - \rho^\ast v_x^\ast = S_\alpha \rho_\alpha - \rho_\alpha v_{x, \alpha} \tag{7}\] \[S_\alpha \rho^\ast v_x^\ast - (\rho^\ast v_x^\ast v_x^\ast + P_\mathrm{tot}^\ast - B_x B_x) = S_\alpha \rho_\alpha v_{x, \alpha} - (\rho_\alpha v_{x, \alpha} v_{x, \alpha} + P_{\mathrm{tot}, \alpha} - B_x B_x) \tag{8}\]すると\(\alpha = R, L\)より、この4本の方程式には\(\rho^\ast, v_x^\ast, P_\mathrm{tot}^\ast\)の3つの変数しかありません。よってこれを解いて\(\rho^\ast\)などを得ることは不可能です。 この議論から、断熱HLLDのときと同様に\(\rho^\ast, v_x^\ast\)はHLL中間状態から求めることにしましょう。すなわち
\[\rho^\ast = \rho_\mathrm{HLL}^\ast = \frac{S_R \rho_R - S_L \rho_L - \rho_R v_{x, R} + \rho_L v_{x, L}}{S_R - S_L} \tag{9}\]そして\(\rho v_x\)のHLL中間状態は、HLL法の(8)式から求めることにすると
\[(\rho v_x)_\mathrm{HLL}^\ast = \frac{S_R \rho_L v_{x, L} - S_L \rho_R v_{x, R} + S_R S_L (\rho_R - \rho_L)}{S_R - S_L} \tag{10}\]より
\[v_x^\ast = \frac{(\rho v_x)_\mathrm{HLL}^\ast}{\rho_\mathrm{HLL}^\ast} = \frac{S_R \rho_L v_{x, L} - S_L \rho_R v_{x, R} + S_R S_L (\rho_R - \rho_L)}{S_R \rho_R - S_L \rho_L - \rho_R v_{x, R} + \rho_L v_{x, L}} \tag{11}\]と求まります。さらに\(P_\mathrm{tot}^\ast\)は(8)式から求めましょう。 しかし(8)式において\(\rho^\ast, v_x^\ast\)はHLL中間状態から求めたことからわかるように、\(P_\mathrm{tot}^\ast\)もHLL中間状態から求めたものに一致します。
続いて\(v_{y, \alpha}^\ast\)を求めてみましょう。これは断熱HLLDの場合と変わりないため、その式を流用します。断熱HLLDの(14)式において\(S_M = v_x^\ast\)とすると
ここで、この式の分数部分の分母を整理しましょう。
\[\rho_\alpha (S_\alpha - v_{x, \alpha}) (S_\alpha - v_x^\ast) - B_x^2 = \rho^\ast \left\{ \frac{\rho_\alpha}{\rho^\ast} (S_\alpha - v_{x, \alpha}) (S_\alpha - v_x^\ast) - \frac{B_x^2}{\rho^\ast}\right\}\](6)式の第一式より
\[\rho^\ast = \frac{S_\alpha - v_{x, \alpha}}{S_\alpha - v_x^\ast} \rho_\alpha\]を代入すると
\[\rho^\ast \left\{ (S_\alpha - v_x^\ast)^2 - \frac{B_x^2}{\rho^\ast} \right\} = \rho^\ast \left( S_\alpha - v_x^\ast - \frac{\vert B_x\vert}{\sqrt{\rho^\ast}}\right) \left( S_\alpha - v_x^\ast + \frac{\vert B_x\vert}{\sqrt{\rho^\ast}}\right) = \rho^\ast (S_\alpha - S_R^\ast) (S_\alpha - S_L^\ast)\]のように整理されます。よって
\[\rho^\ast v_{y, \alpha}^\ast = \rho^\ast v_{y, \alpha} - \frac{v_x^\ast - v_{x, \alpha}}{(S_\alpha - S_R^\ast)(S_\alpha - S_L^\ast)} B_{y, \alpha} B_x \tag{12}\]同様に、断熱HLLDの(16)式より
\[\rho^\ast v_{z, \alpha}^\ast = \rho^\ast v_{z, \alpha} - \frac{v_x^\ast - v_{x, \alpha}}{(S_\alpha - S_R^\ast)(S_\alpha - S_L^\ast)} B_{z, \alpha} B_x \tag{13}\] \[B_{y, \alpha}^\ast = B_{y, \alpha} \frac{\rho_\alpha (S_\alpha - v_{x, \alpha})^2 - B_x^2}{\rho_\alpha (S_\alpha - v_{x, \alpha}) (S_\alpha - v_x^\ast) - B_x^2} = B_{y, \alpha} \frac{\rho_\alpha (S_\alpha - v_{x, \alpha})^2 - B_x^2}{\rho^\ast (S_\alpha - S_R^\ast) (S_\alpha - S_L^\ast)} \tag{14}\] \[B_{z, \alpha}^\ast = B_{z, \alpha} \frac{\rho_\alpha (S_\alpha - v_{x, \alpha})^2 - B_x^2}{\rho^\ast (S_\alpha - S_R^\ast) (S_\alpha - S_L^\ast)} \tag{15}\]となります。求まっていないのは\(\mathbf{U}_c\)での\(v_{y, c}, v_{z, c}, B_{y, c}, B_{z, c}\)です。 これらも断熱HLLDと同様の計算で求めることができます。断熱HLLDの(27)式において\(\rho_L^\ast = \rho_R^\ast = \rho^\ast\)とすれば
\[\begin{align} &v_{y, c}^\ast = \frac{\sqrt{\rho^\ast} v_{y, L}^\ast + \sqrt{\rho^\ast} v_{y, R}^\ast + (B_{y, R}^\ast - B_{y, L}^\ast) \mathrm{sign} (B_x)}{\sqrt{\rho^\ast} + \sqrt{\rho^\ast}} \notag \\ &\Longrightarrow \ \rho^\ast v_{y, c}^\ast = \frac{\rho^\ast v_{y, L}^\ast + \rho^\ast v_{y, R}}{2} + \frac{(B_{y, R}^\ast - B_{y, L}^\ast) \sqrt{\rho^\ast} \mathrm{sign} (B_x)}{2} \tag{16} \end{align}\]同様に断熱HLLDの(28)式より
\[\rho^\ast v_{z, c}^\ast = \frac{\rho^\ast v_{z, L}^\ast + \rho^\ast v_{z, R}}{2} + \frac{(B_{z, R}^\ast - B_{z, L}^\ast) \sqrt{\rho^\ast} \mathrm{sign} (B_x)}{2} \tag{17}\]です。そして断熱HLLDの(29)式より
\[B_{y, c}^\ast = \frac{\sqrt{\rho^\ast} B_{y, R}^\ast + \sqrt{\rho^\ast} B_{y, L}^\ast + \rho^\ast (v_{y, R}^\ast - v_{y, L}^\ast) \mathrm{sign}(B_x)}{2 \sqrt{\rho^\ast}} = \frac{B_{y, R}^\ast + B_{y, L}^\ast}{2} + \frac{(v_{y, R}^\ast - v_{y, L}^\ast) \sqrt{\rho^\ast} \mathrm{sign} (B_x)}{2} \tag{18}\]最後に断熱HLLDの(30)式から
\[B_{y, c}^\ast = \frac{B_{z, R}^\ast + B_{z, L}^\ast}{2} + \frac{(v_{z, R}^\ast - v_{z, L}^\ast) \sqrt{\rho^\ast} \mathrm{sign} (B_x)}{2} \tag{19}\]と求まります。
数値計算に用いる
HLL, HLLC, 断熱HLLDと同様に、実際の数値計算では\(S_L, S_L^\ast, S_R^\ast, S_R\)の大きさに依存して、どの流束を用いるかを決定します。 下図は左上から\(S_L > 0, S_L \leq 0 < S_L^\ast, S_L^\ast \leq 0 S_R^\ast, S_R^\ast \leq 0 < S_R, S_R \leq 0\)の場合を図示したものです。
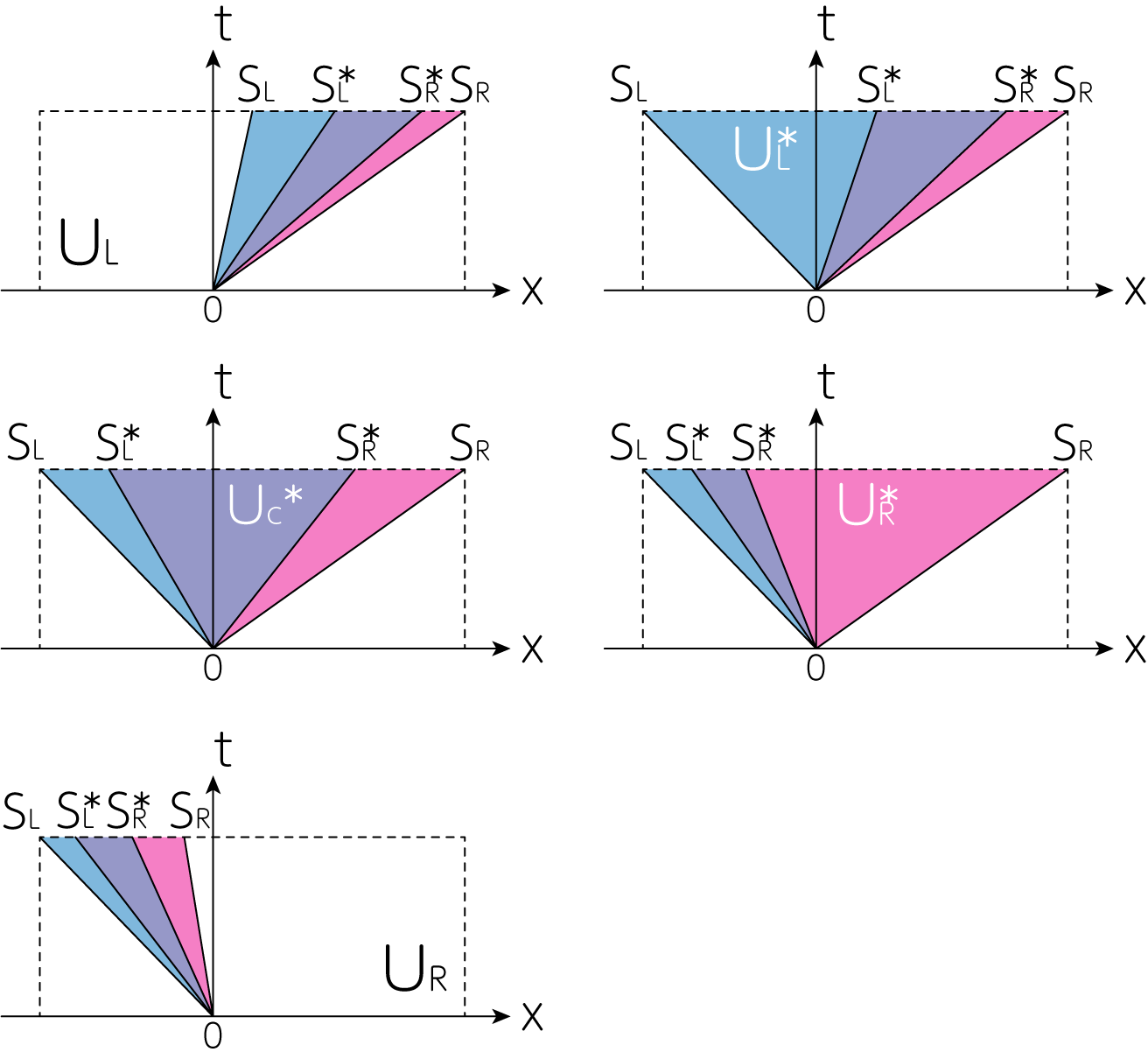
よって、数値計算を行う場合に、その流束の選択は
\[\mathbf{F}_\mathrm{iso \ HLLD} = \left\{ \begin{array}{ll} \mathbf{F}_L & \mathrm{if} \ S_L > 0 \\ \mathbf{F}_L^\ast = \mathbf{F}_L + S_L (\mathbf{U}_L^\ast - \mathbf{U}_L) & \mathrm{if} \ S_L \leq 0 < S_L^\ast \\ \mathbf{F}_c^\ast & \mathrm{if} \ S_L^\ast \leq 0 < S_R^\ast \\ \mathbf{F}_R^\ast = \mathbf{F}_R + S_R (\mathbf{U}_R^\ast - \mathbf{U}_R)& \mathrm{if} \ S_R^\ast < 0 < S_R \\ \mathbf{F}_R & \mathrm{if} \ S_R \leq 0 \end{array} \right. \tag{20}\]のようにします。
等温HLLD流束の計算モジュール
以下に等温HLLD流束計算コードのJulia実装例を示します。
function hlld_core(rol, vnl, vtl, vul, prl, bnl, btl, bul, ror, vnr, vtr, vur, prr, bnr, btr, bur, cs2)
# compute B * B at left side
bl2 = dot([bnl, btl, bul], [bnl, btl, bul])
# compute fast-mode speed at left side
vfl = sqrt(((bl2+prl)+sqrt((bl2+prl)^2-4*prl*bnl^2))/(2*rol))
# compute B * B at right side
br2 = dot([bnr, btr, bur], [bnr, btr, bur])
# compute fast-mode speed at right side
vfr = sqrt(((br2+prr)+sqrt((br2+prr)^2-4*prr*bnr^2))/(2*ror))
# compute sl, sr
sl = min(vnl, vnr) - max(vfl, vfr)
sr = max(vnl, vnr) + max(vfl, vfr)
# compute bnc from HLL average
bnc = (sr*bnr-sl*bnl) / (sr-sl)
# compute pt at left and right sides
ptl = prl + 0.5 * bl2
ptr = prr + 0.5 * br2
# compute ro from HLL average at intermediate state
srsl = sr - sl
roi = (sr*ror-sl*rol-ror*vnr+rol*vnl) / srsl
# compute Fhll for density flux
Fhllro = (sr*rol*vnl-sl*ror*vnr+sr*sl*(ror-rol)) / srsl
# compute Fhll for x-momentum flux
Fmnl = rol * vnl * vnl + ptl - bnc * bnc
Fmnr = ror * vnr * vnr + ptr - bnc * bnc
Fhllmn = (sr*Fmnl-sl*Fmnr+sr*sl*(ror*vnr-rol*vnl)) / srsl
# compute vn at inbermediate state
vni = Fhllro / roi
# compute sl*, sr*
rtroi = sqrt(roi)
sli = vni - abs(bnc) / rtroi
sri = vni + abs(bnc) / rtroi
# compute my, mz, by, bz at left inner side in Riemann fan
if abs((sl-sri)*(sl-sli)) > 1.0e-10
denol = 1.0 / ((sl-sri)*(sl-sli))
mtil = roi * vtl - (vni-vnl) * denol * btl * bnc
muil = roi * vul - (vni-vnl) * denol * bul * bnc
btil = btl * (rol*(sl-vnl)^2-bnc^2) * denol / roi
buil = bul * (rol*(sl-vnl)^2-bnc^2) * denol / roi
else
mtil = rol * vtl
muil = rol * vul
btil = btl
buil = bul
end
# compute my, mz, by, bz at right inner side in Riemann fan
if abs((sr-sri)*(sr-sli)) > 1.0e-10
denor = 1.0 / ((sr-sri)*(sr-sli))
mtir = roi * vtr - (vni-vnr) * denor * btr * bnc
muir = roi * vur - (vni-vnr) * denor * bur * bnc
btir = btr * (ror*(sr-vnr)^2-bnc^2) * denor / roi
buir = bur * (ror*(sr-vnr)^2-bnc^2) * denor / roi
else
mtir = ror * vtr
muir = ror * vur
btir = btr
buir = bur
end
# compute my, mz, by, bz at middle inner side in Riemann fan
signbn = sign(bnc)
mtic = 0.5 * (mtil+mtir+(btir-btil)*rtroi*signbn)
muic = 0.5 * (muil+muir+(buir-buil)*rtroi*signbn)
btic = 0.5 * (btil+btir+(mtir-mtil)*signbn/rtroi)
buic = 0.5 * (buil+buir+(muir-muil)*signbn/rtroi)
# choose flux
if sl > 0.0
Ultmp = [rol, rol*vnl, rol*vtl, rol*vul, bnl, btl, bul]
Fresult = Convert.u_to_f(Ultmp, cs2)
elseif sl <= 0.0 < sli
Ultmp = [rol, rol*vnl, rol*vtl, rol*vul, bnl, btl, bul]
Ulitmp = [roi, roi*vni, mtil, muil, bnc, btil, buil]
Fltmp = Convert.u_to_f(Ultmp, cs2)
Fresult = Fltmp + sl * (Ulitmp-Ultmp)
elseif sli <= 0.0 < sri
Fresult = [roi*vni, Fhllmn, mtic*vni-btic*bnc, muic*vni-buic*bnc, 0.0, btic*vni-bnc*mtic/roi, buic*vni-bnc*muic/roi]
elseif sri <= 0.0 < sr
Urtmp = [ror, ror*vnr, ror*vtr, ror*vur, bnr, btr, bur]
Uritmp = [roi, roi*vni, mtir, muil, bnc, btir, buir]
Frtmp = Convert.u_to_f(Urtmp, cs2)
Fresult = Frtmp + sr * (Uritmp-Urtmp)
else
Urtmp = [ror, ror*vnr, ror*vtr, ror*vur, bnr, btr, bur]
Fresult = Convert.u_to_f(Urtmp, cs2)
end
return Fresult
end
function hlld!(F::Array{Float64, 2}, Vl::Array{Float64, 2}, Vr::Array{Float64, 2}, nxmax::Int64, cs2::Float64)
for i in 1:nxmax-1
# set primitive variables at left side
rol = Vl[1, i]
vnl = Vl[2, i]
vtl = Vl[3, i]
vul = Vl[4, i]
bnl = Vl[5, i]
btl = Vl[6, i]
bul = Vl[7, i]
prl = cs2 * rol
# set primitive variables at right side
ror = Vr[1, i]
vnr = Vr[2, i]
vtr = Vr[3, i]
vur = Vr[4, i]
bnr = Vr[5, i]
btr = Vr[6, i]
bur = Vr[7, i]
prr = cs2 * ror
# compute HLLD flux
Fresult = hlld_core(rol, vnl, vtl, vul, prl, bnl, btl, bul, ror, vnr, vtr, vur, prr, bnr, btr, bur, cs2)
# convert flux and input to F
F[:, i] = Fresult
end
end
例えば全圧力\(P_\mathrm{tot} = P_\mathrm{gas} + \frac{1}{2} B^2\)を計算する際には、ガス圧\(P_\mathrm{gas}\)が必要になります。その場合には以下の関係式を用います。
\[C_s^2 = \frac{P_\mathrm{gas}}{\rho} \ \Longrightarrow \ P_\mathrm{gas} = C_s^2 \rho \tag{21}\]等温の場合、音速\(C_s\)は一定・一様な値になります。この値をあらかじめ初期条件として定めておくことで、計算を進めることができます。
初期条件として
そして\(C_s = 1.0\)とした場合に、上述のJulia実装で計算された等温磁気流体衝撃波の時間発展を以下に示します。
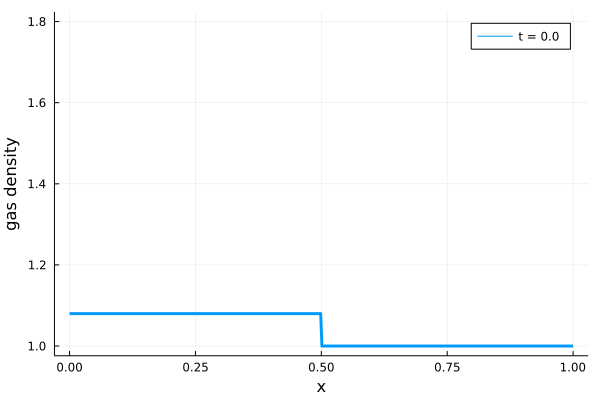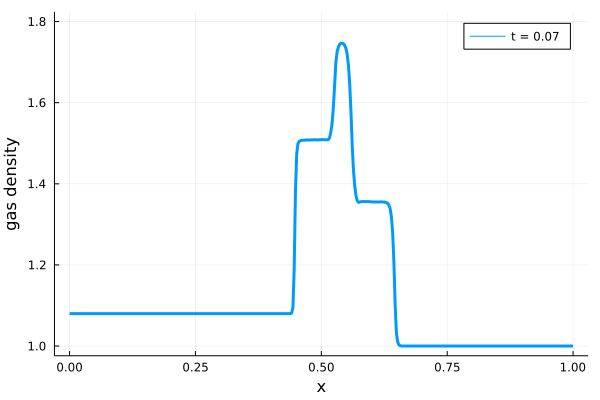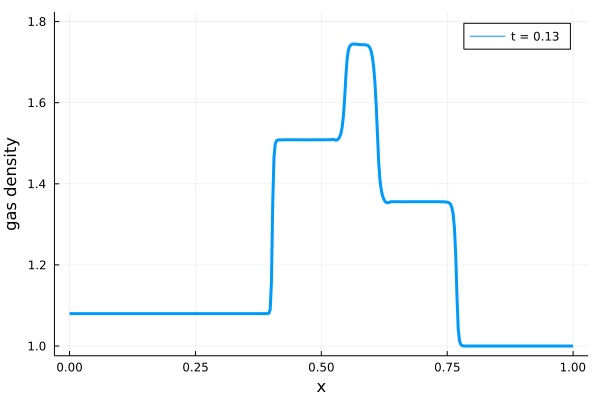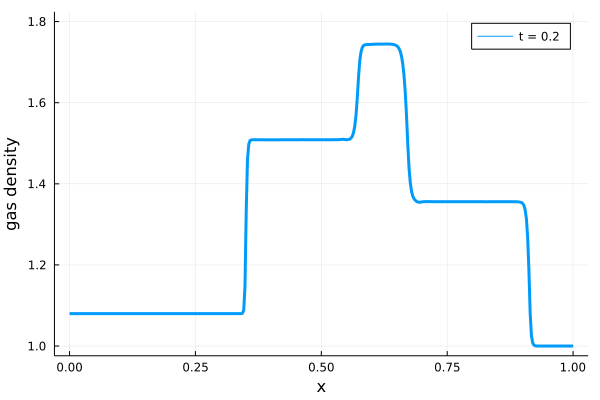
参考文献