Table of contents
超新星爆発に至る大質量星中心部の進化
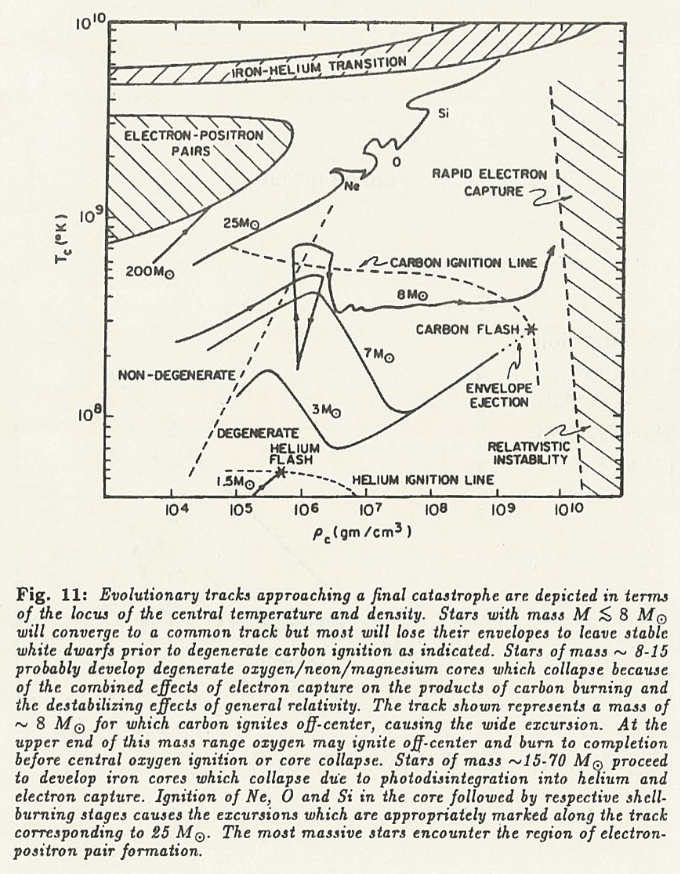
中心部でのヘリウム燃焼段階以後の進化は、C-O中心核が縮退するかどうかによって大きく変わります。 ガスが理想気体に近い場合には、恒星中心温度は収縮とともに上昇するが、密度が高くなり電子が縮退した状態になると、収縮とともに温度が下がります。 そのため、星ほ中心温度には(質量に依存する)最大値が存在します。 その最大中心温度のおおよその値を求めてみましょう。 中心温度の最大値\(T_\mathrm{cmax}\)は、理想気体圧力と縮退圧とが同程度になったときに達成されるため
\[\frac{k_B}{\mu_mathrm{e} m_\mathrm{p}} \rho_\mathrm{c} T_\mathrm{cmax} \simeq 1.0 \times 10^{13} \left( \frac{\rho_\mathrm{c}}{\mu_\mathrm{c}}\right)^{5/3} \tag{1}\]という関係を用いることができます。 左辺は理想気体の圧力、右辺が非相対論的な縮退圧を表します。 C-O中心核では、イオンの平均分子量\(\mu_\mathrm{I}>12\)に対して、電子平均分子量\(\mu_\mathrm{e} \sim 2\)なので、理想気体圧力のイオンの効果は無視されています。
これはガスの状態方程式から得られる関係ですが、圧力と密度の関係は静水圧平衡の式をもとにしても得ることができます。 進化の進んだ星では中心核と外層の密度差が大きいため、中心部の物理的な性質は外層質量に依存せず、中心核の質量のみで決定されます (中心核と外層の境界の圧力は中心部の圧力に比べ非常に小さいため、そこを表面として考えても内部構造にはほぼ影響しません。) 中心での圧力\(P_\mathrm{c}\)は静水圧平衡の式
と書けます。 ここで\(R_c\)は中心核の半径、またバーは中心核での平均値を表し、\(\overline{r^2} \simeq \frac{R_c^2}{4}\)としました。 また上式の最後の関係には\(M_c = \frac{4\pi}{3} R_c^3 \overline{\rho}\)の関係を用いました。 この式に、理想気体圧力と縮退圧とが同程度である(\(P \sim 2 P_\mathrm{idela}\))を用いると
\[\frac{2k_B}{\mu_e m_p} \rho_c T_{c, \mathrm{max}} \approx 4 \left(\frac{4\pi}{3} \right)^{1/3} GM_c^{2/3} \overline{\rho}^{4/3}\]の関係が得られます。 非相対論的に縮退したガスは、指数\(n = 1.5\)のポリトロープであることが知られています。 \(n=1.5\)のポリトロープガス球の関係\(\rho_c / \overline{\rho} \sim 5.991\)より
\[T_{c, \mathrm{max}} \rho_c^{-1/3} \simeq 2 \cdot 6^{-4/3} \left( \frac{4\pi}{3} \right)^{1/3} \frac{\mu_e m_p}{k_B} G M_c^{2/3} \tag{3}\]が得られます。 (1), (3)式より
\[\rho_c^{1/3} \simeq 2 \cdot 6^{-4/3} 10^{-13} \left( \frac{4\pi}{3}\right)^{1/3} G \mu_e^{5/3} M_c^{2/3}\] \[T_{c, \mathrm{max}} \simeq 4 \cdot 6^{-8/3} 10^{-13} \left( \frac{4\pi}{3}\right)^{2/3} \frac{m_p}{k_B} G^2 (\mu_e^2 M_c)^{4/3} \simeq 7.4 \times 10^8 \left( \frac{\mu_e}{2} \right)^{8/3} \left( \frac{M_c}{M_\odot}\right)^{4/3}\]が得られます。 これは太陽質量より質量の大きいC-O中心核が、強い縮退状態になる以前の段階で、炭素燃焼点火温度以上になることを表しています。 これは、主系列星段階での質量\(\gtrsim 8 M_\odot\)に対応します (この質量の下限は質量放出率に依存します。)
種々の初期質量範囲に対する最終進化は、以下のように考えられています (ただし各質量範囲の境界は質量放出率に依存するため不確定です。)
- \(M \lesssim 8 M_\odot\): 炭素燃焼が起こらず、外層を失って白色矮星となります。もしそれが連星系内にあり、伴星から質量を得て\(\sim 1.4 M_\odot\)となると、pycnonuclear reactionによる炭素の爆発的燃焼(carbon flash)が始まり、Ia型超新星となります。
- \(8 M_\odot \lesssim M \lesssim 11M_\odot\): 安定な炭素燃焼によってできたO-Ne-Mg中心核が強く縮退し、電子のフェルミエネルギーがMg, Neの電子捕獲反応に対する閾値エネルギーを超えます。電子捕獲反応により、圧力のもとになっている電子が減少するため、重力崩壊 (electron-capture supernova)を起こし、中性子星が形成されます。この進化に対する質量の境界は、質量放出率などから不確定です。
- \(11 M_\odot \lesssim M \lesssim 100 M_\odot\): 中心部での核融合反応はシリコン燃焼まで進み、鉄の中心核(\(\sim 1.4 M_\odot\))が形成されます。温度が\(\sim 10^{10} \mathrm{K}\)で鉄の原子核が光子によって壊され、重力崩壊します。中心部は中性子星となり、外層はII型超新星爆発を起こして吹き飛ばされます。\(M>30M_\odot\)の場合は爆発を起こす前に、恒星風によって水素を多く含む外層を失いWolf-Rayet星になっているため、Ib型超新星になると考えられています。 また\(M \gtrsim 50 M_\odot (?)\)の場合、中心部の崩壊によってブラックホールが形成され、爆発を起こさない可能性も考えられます。
- \(M \gtrsim 100 M_\odot\): 安定な炭素燃焼後、\(e^- e^+\)対生成が多く起こる\((\rho, T)\)状態になります。この反応は吸熱反応(熱エネルギーから電子陽電子の静止質量)であるため、\(\gamma < 4/3\)となり不安定となります (収縮して温度が上昇すると\(e^- e^+\)対生成率が上昇し、収縮を続けます。)中心核が崩壊し温度が十分高くなると、爆発的な酸素燃焼が起こります。すると崩壊が止められ、バウンスにより超新星爆発が起こります。しかし質量が大きすぎると、爆発的酸素燃焼によっても崩壊が止められず、ブラックホールになると考えられています。\(e^- e^+\)対生成不安定が起こるためには、炭素燃焼段階までに質量損失段階で質量が減少しないことが必要なので、重元素がほとんどないために質量損失が抑えられる種族III(pop-III)の大質量星で起こると考えられています。
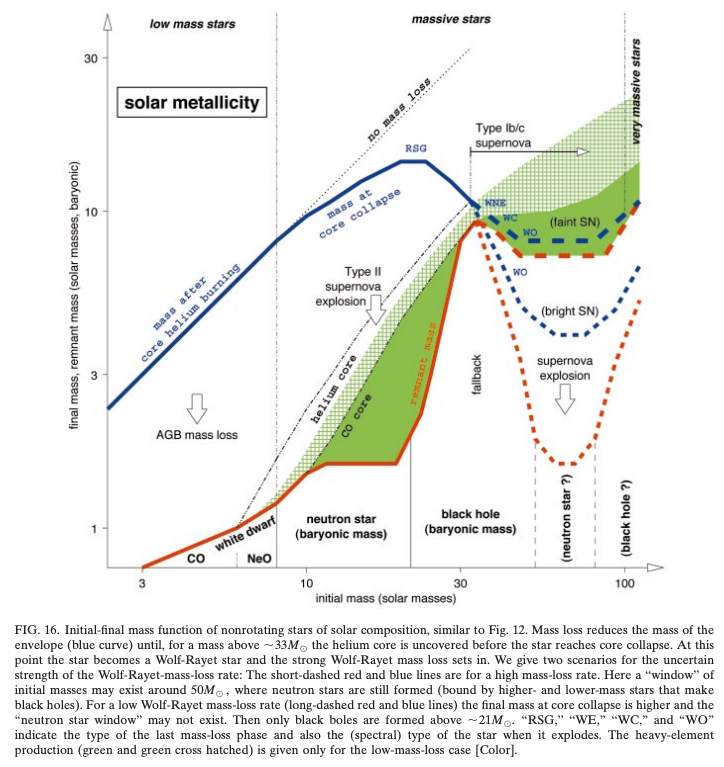
次の図は恒星の初期質量(横軸)と最終質量(縦軸)を、太陽金属量の場合に図示したものです。 恒星風の質量損失により、最終質量は初期状態から大きく減少していることがわかります。
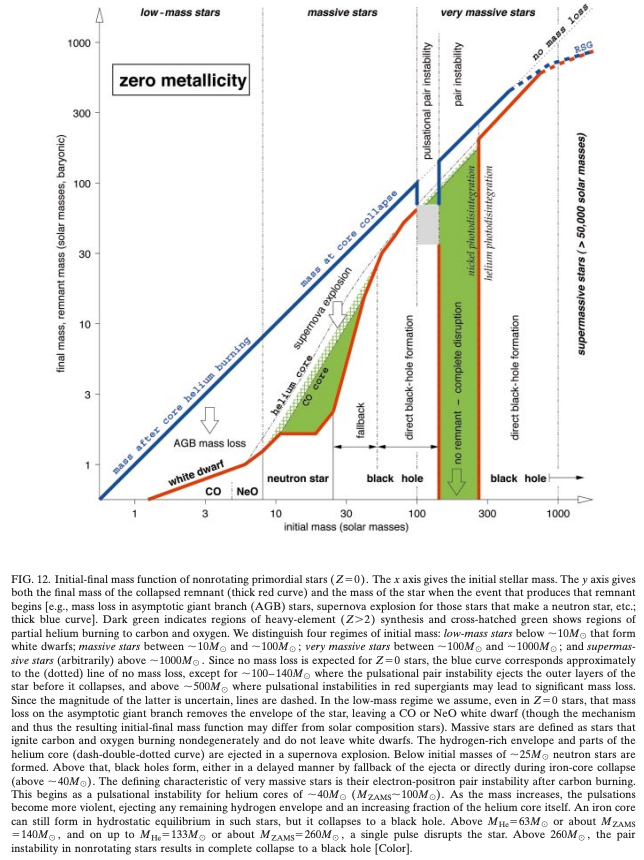
そして次の図は、金属量がゼロ(\(Z = 0\))の場合について描画したものです。 \(Z=0\)であることにより、質量損失が著しく抑制されていることがわかります。
最近の話題: 電子捕獲型超新星の発見
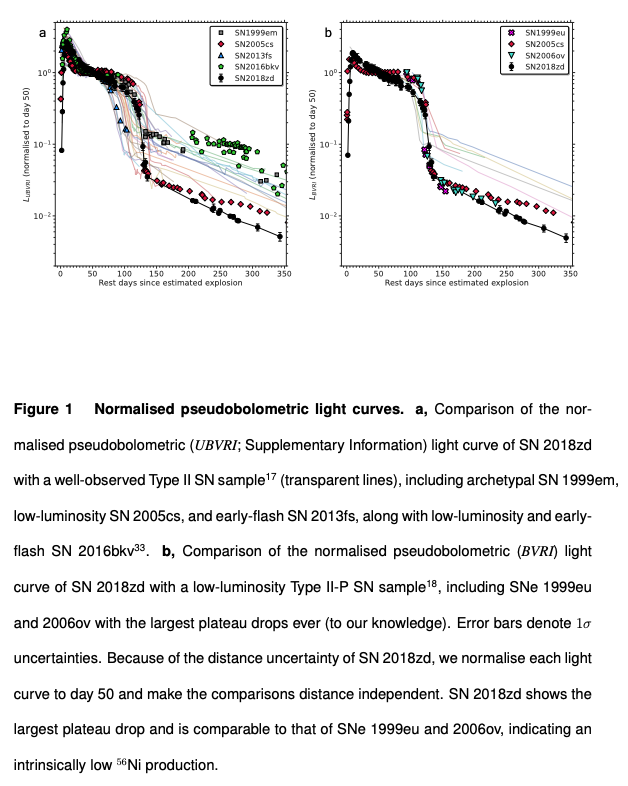
白色矮星と鉄コア崩壊型超新星の間の質量範囲\(8 \sim 10 M_\odot\)では、電子捕獲型超新星が起こるとされています。 この超新星は、Miyaji et al. (1980)で理論的に提唱されましたが、\(8 \sim 10 M_\odot\)という狭い質量範囲の恒星が超新星爆発を起こさなければならないというレアさから、これまで対応天体が発見されていませんでした。 しかし最近になり、SN 2018zdという超新星が、電子捕獲型超新星の強い候補である論文が出版されました (Hiramatsu et al. (2021)。)
この論文では、星周物質・化学組成や爆発のエネルギーから、2018zdを電子捕獲型超新星と結論づけています。 しかしその質量範囲の狭さから、これは電子捕獲型ではなく、低質量赤色超巨星からの鉄のコア崩壊型超新星爆発ではないかという反証論文も発表されました (Callis et al. (2021)。) 先程のHiramatsu et al. (2021)の論文の前にも、SN 2018zdは\(12 M_\odot\)のII型超新星爆発であるという論文も出版されており、まだまだ議論の余地がありそうです(Zhang et al. (2020)。)
参考文献
[1] Wooskey et al., 2002, “The evolution and explosion of massive stars”
[2] Miyaji et al., 1980, “Supernova triggered by electron captures”
[3] Hiramatsu et al., 2021, “The electron-capture origin of supernova 2018zd”
[4] Callis et al., 2021, “How low can you go? SN 2018zd as a low-mass Fe core-collapse supernova”
[5] Zhang et al., 2020, “SN 2018zd: an unusual stellar explosion as part of the diverse Type II Supernova landscape”
[6] Kippenhahn, Weigert & Weiss, “Stellar Structure and Evolution”
[7] 野本憲一, 定金晃三, 佐藤勝彦, “恒星”