Table of contents
磁気ミラーと2次のフェルミ加速
ここでは磁気ミラーとして知られる、静磁場を用いた荷電粒子の閉じ込め機構についてまとめました。 さらにこれを用いた粒子加速機構であるフェルミ加速についてもメモしています。
非一様な磁場中での粒子の運動: 磁場に沿う力
解析力学の復習から入りましょう。 準周期運動を行っている粒子に対しては、座標\(q\)とそれに共役な運動量\(p\)において、その作用積分
\[J = \oint p dq \tag{1}\]は、系を特徴づけるパラメータのゆっくりした変化に対して保存量となります。 ここで\(\oint\)は、粒子の運動の1周期についての積分です。 磁場中でサイクロトロン運動する粒子に、この式を適用してましょう。 まず\(q \rightarrow x, p \rightarrow mv_x\)とすると
\[J_1 = \oint m v_x dx = \int_0^{2\pi / \omega_c} mv_\perp^2 \cos^2 (\omega_c t) dt = \frac{\pi m v_\perp^2}{\omega_c} = \left(\frac{2\pi mc}{q}\right) \left(\frac{W_\perp}{B}\right) \tag{2}\]のように計算されます。 途中の積分計算では、\(dx = \frac{dx}{dt} dt = v_x dt\)のように置換を行い、さらにサイクロトロン運動における\(x\)方向の速度を\(v_x = v_\perp \cos (\omega_c t)\)のようにしました。 さらに磁場に垂直な方向の運動エネルギーを\(W_\perp \equiv \frac{1}{2}m v_\perp^2\)のように定義しました。 解析力学の知識から、(2)式に現れた\(\mu \equiv W_\perp / B\)は保存量となります。 この\(\mu\)は粒子の磁気モーメントです (\(\mu\)が磁気モーメントであることの説明を補遺として記載しました。)
以降では、下図のように空間的に収束していく磁力線に沿って運動する粒子に働く力を考えましょう。
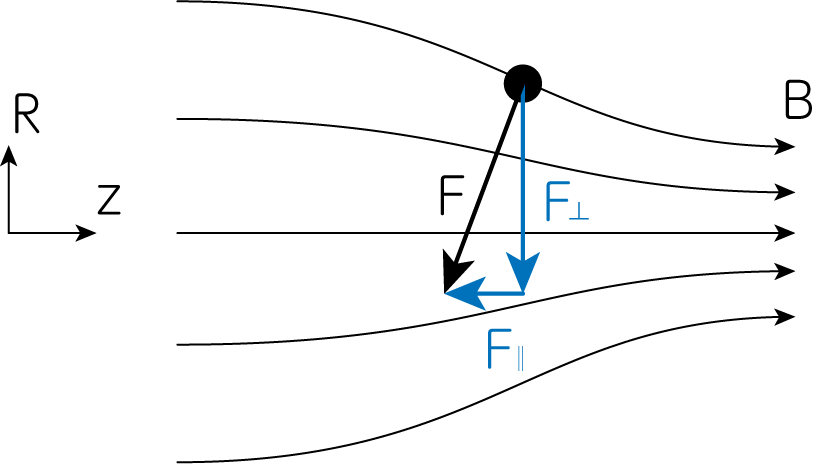
ただし、\(B_\varphi\)は至る所でゼロ、さらに軸対称な磁場を考え\(R=0\)で\(B_R = 0\)とします。 また\(B_z \gg B_R\)のように\(z\)方向の磁場が卓越しており、\(\frac{\partial B_z}{\partial z}\)は\(R\)に依存せずほぼ一定であるとします。 粒子に働くローレンツ力を、磁場に沿った方向\(F_\parallel\)と磁場に垂直な方向\(F_\perp\)に分けて考えましょう。 すると\(B_z \gg B_R\)の仮定から、\(F_\parallel \approx F_z\)と考えられため
\[\mathbf{F}_\parallel \approx - \frac{q}{c} v_\varphi B_R \mathbf{e}_z \tag{3}\]となります。 また磁場はマクスウェル方程式から
\[\nabla \cdot \mathbf{B} = \frac{1}{R} \frac{\partial}{\partial R} (R B_R) + \frac{\partial B_z}{\partial z} = 0 \tag{4}\]を常に満たさなければなりません。 先程の\(\frac{\partial B_z}{\partial z}\)が\(R\)に依存しないという仮定から
\[\frac{\partial}{\partial R} (R B_R) = - R \frac{\partial B_z}{\partial z} \ \Longrightarrow \ R B_R = - \frac{1}{2} R^2 \frac{\partial B_z}{\partial z} + C \ \Longrightarrow \ B_R = - \frac{1}{2} R \frac{\partial B_z}{\partial z} + \frac{C}{R} \tag{5}\]のように積分することができます。 \(R \rightarrow 0\)で\(B_z\)が発散しないために、積分定数は\(C = 0\)となります。 荷電粒子の運動は\(B_z\)の卓越性から、磁場\(B_z\)によるサイクロトロン運動を行っていると近似して良いでしょう。 するとその粒子の軌道半径は\(R = v_\varphi / \omega_c\)となります。 以上より
\[\mathbf{F}_\parallel = - \frac{qR v_\varphi}{2c} \frac{\partial B_z}{\partial z} = - \frac{qv_\varphi^2 }{2c \omega_c} \frac{\partial B_z}{\partial z} \underbrace{=}_{\omega_c = qB / mc} - \frac{\frac{1}{2} m v_\varphi^2}{B} \frac{\partial B_z}{\partial z} = - \mu \frac{\partial B_z}{\partial z} \tag{6}\]のように計算されます。 途中、\(B_z\)によるサイクロトロン運動が卓越していることから\(v_\varphi \sim v_\perp\)のようにし、さらに磁気モーメントの定義を用いました。 このような磁場構造を持つ空間を荷電粒子が運動すると、磁場に沿った方向に力を受けることがわかりました。
地球磁気圏での荷電粒子の運動と捕捉条件
これらから、このように磁力線の両端をしぼった磁気瓶(ミラー装置)や地球の磁力線中の荷電粒子の運動を、磁気モーメント保存とエネルギー保存則を用いて調べることができます。 より応用を意識して、ここでは地磁気中の荷電粒子の運動について考察してみましょう。
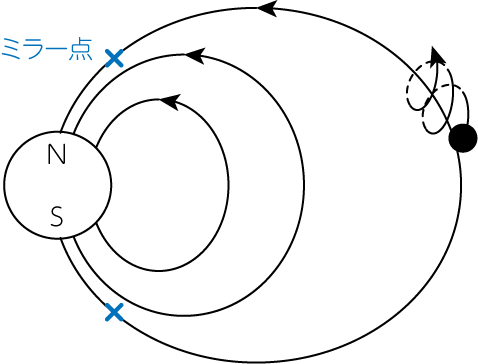
地球の磁場強度は、磁力線が収束する両極付近で強く、赤道付近では弱くなっています。 特に地球磁場は双極子磁場であるため、磁場強度は\(1/r^3\)に比例して地球中心からの距離\(r\)とともに減少します。 最大磁場強度と最小磁場強度では、その比は\(10^4\)にも達すると言われるほどです。 荷電粒子は磁力線に巻き付くように運動しながら、磁力線が収束する両極(地球では電離層上空)付近で(6)式で表される力を受けます。 これにより荷電粒子は反射され、両極地方の間の往復運動を行います。 これはバウンス運動(bounce motion)と呼ばれています。
(6)式を見ると、磁場に沿った方向の力は\(\mu\)に比例することがわかります。 つまり、もし\(\mu\)が小さいと磁場に沿った方向の力が弱くなり、バウンス運動するような捕捉が起こらないことがわかります。 そこで、ここでは捕捉条件を求めることにしましょう。 ミラー磁場中に荷電粒子が閉じ込められるには、荷電粒子が磁力線に沿って端に到達する以前に\(v_\parallel = 0\)となる必要があります。 このときの\(v_\perp\)を\(v_\perp'\)のように書き、さらにその場所での磁場を\(B'\)のように表記します。 \(\mu\)の保存から
となり、そしてエネルギー保存から
\[v_\perp'^2 = v_{\perp, 0}^2 + v_{\parallel, 0}^2 \equiv v_0^2 \tag{8}\]を得ます。 これら二式から
\[\frac{B_0}{B'} = \frac{v_{\perp, 0}^2}{v_\perp'^2} = \frac{v_{\perp, 0}^2}{v_0^2} = \sin^2 \alpha \tag{9}\]のようになります。 ここで\(\theta\)は、弱磁場領域での荷電粒子の螺旋運動のピッチ角です。 ここからわかるように、より小さな\(\alpha\)を持つ粒子は、より大きな磁場\(B'\)の部分で反射することがわかります。 もし\(\alpha\)が小さすぎると、\(B'\)が磁場の最大値\(B_m\)を越え、粒子は反射することなく抜け出してしまいます。 (9)式において\(B' \rightarrow B_m\)のように置き換えれば、捕捉される荷電粒子の最小の\(\alpha\)を求めることができます。
\[\sin^2 \alpha_m = \frac{B_0}{B_m} \equiv \frac{1}{R_m} \tag{10}\]ここで\(R_m\)をミラー比と呼びます。 またミラー磁場により反射が起こる場所を、ミラー点(mirror point)などと呼びます。 (10)式は、速度空間上でロスコーン (loss cone)と呼ばれる円錐を形成します。

このロスコーン中に存在する荷電粒子はミラー磁場に閉じ込めることはできません。 そのため、ミラーで閉じ込められるプラズマは等方的な速度分布ではなくなります。 またロスコーンの式(10)には\(q, m\)が含まれていないことからもわかるように、(衝突などの他の効果がなければ)イオンも電子も同様に閉じ込められることがわかります。
ミラー型磁場の捕捉を免れた荷電粒子は、通過粒子として磁力線に沿って系外に失われます。 こうして、電離層に降り注ぐ荷電粒子(主に電子)が酸素原子や窒素原子などを衝突励起し、その脱励起に際しての発光がオーロラとして観測されます。
フェルミ加速 (Fermi acceleration)
先程までの議論から、下図のようなミラー磁場中に捕捉された荷電粒子は、磁力線に沿って往復運動を行います。
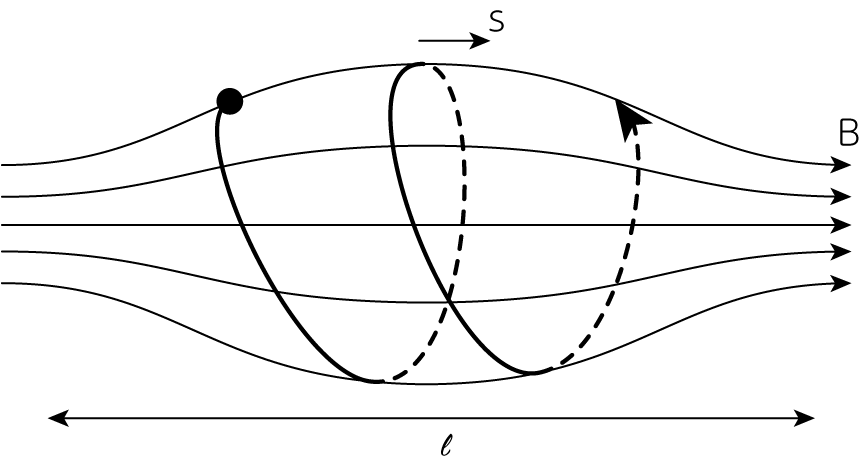
ここから、この周期運動の第二の作用積分を考えることができます。 磁力線に沿った座標を\(s\)とすると
\[J_2 = \oint mv_\parallel ds \tag{11}\]も、断熱不変量となります。 磁力線に沿った方向の平均的な速度を\(\langle v_\parallel \rangle\)、そしてミラー磁場の長さを\(\ell\)とすると
\[J_2 \approx 2 m \langle v_\parallel \rangle \ell \tag{12}\]のように計算できます。 \(J_2\)が保存されることから、ミラー磁場の長さ\(\ell\)を小さくすることで\(\langle v_\parallel \rangle\)を大きくすることができます。 このような荷電粒子の加速機構を、フェルミ加速(Fermi acceleration)と呼びます。
星間乱流による宇宙線の加速 (2次のフェルミ加速: 2nd order Fermi acceleration)
星間空間には乱流が存在し、それによって磁力も複雑な形状をします。 すると星間空間には、ミラー磁場のようなすぼまった磁場形状を伴う星間雲が至るところに存在すると考えて良いでしょう。 これにより荷電粒子は星間雲と衝突を繰り返し、その運動方向や速度を変化させながら運動すると考えることができます。

簡単のため、ミラー磁場を伴う星間雲が速度\(V\)を持って1次元方向に運動しているとします。 ただし\(v \gg V\)とします。 相対論より、荷電粒子の速度と運動量の間には
\[v = \frac{p c^2}{E} \tag{13}\]の関係があります。 下図のように荷電粒子と星間雲が正面衝突する場合を考えましょう。
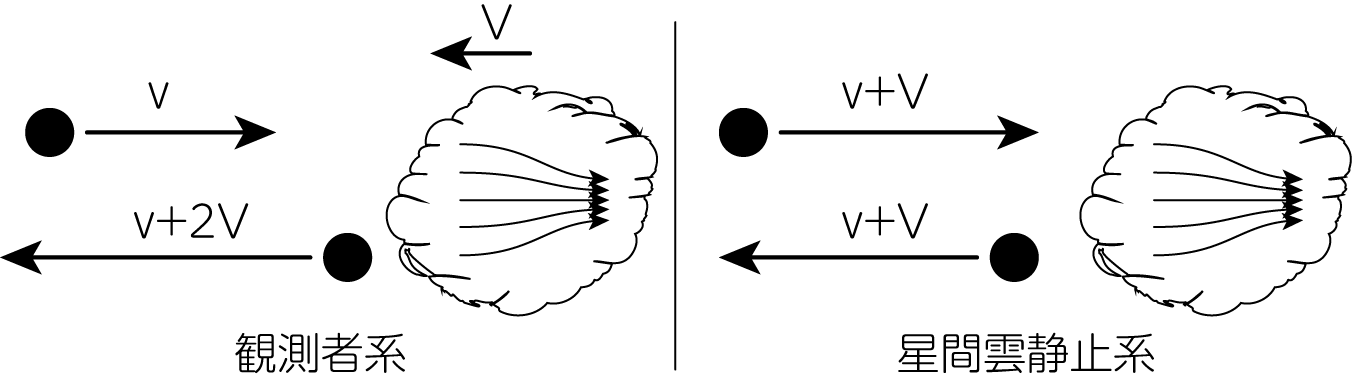
速度\(v\)で星間雲方向に運動する荷電粒子は、星間雲静止系では\(v + V\)で星間雲に向かっているように見えます。 これがミラー磁場により反射されますが、その速度の大きさは変わらずに\(v+V\)のまま、方向だけが180度変わります。 これを再び星間雲が運動して見える観測者系で見ると、最終的に反射された粒子の速度の大きさは\(v+2V\)になることがわかります。 同様のことを星間雲に追突する場合について考えると、最終的な粒子の速度の大きさは\(v-2V\)となります。
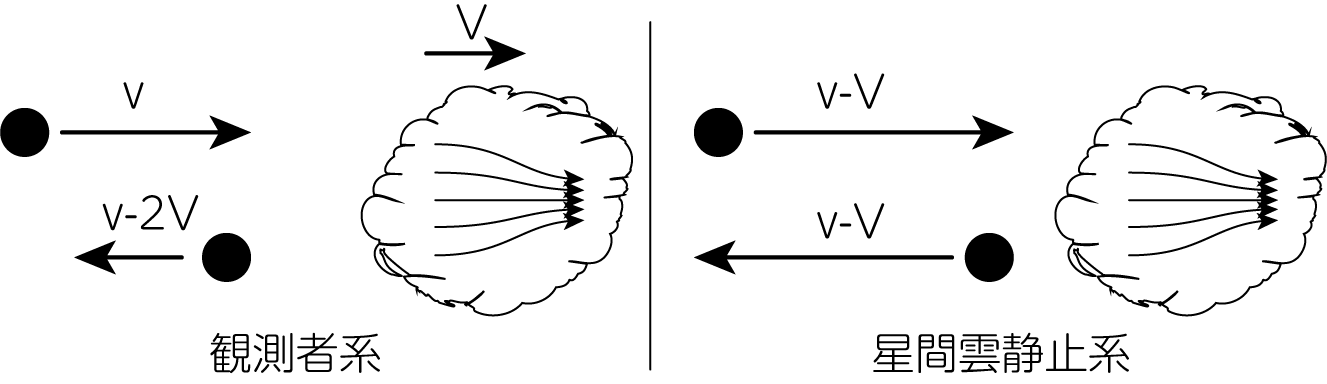
よって荷電粒子の速度の変化は\(\Delta v_{衝突} = 2V\)、そして追突の場合には\(\Delta v_{追突} = -2V\)となります。 すると運動量の変化はそれぞれ
\[\Delta p_{衝突} = \frac{2V E}{c^2}, \quad \Delta p_{追突} = -\frac{2V E}{c^2} \tag{14}\]となります。 ここで、ミラー磁場を伴う星間ガスと荷電粒子との典型的な距離を\(\ell\)とすると、平均衝突時間は\(\Delta t = \frac{\ell}{v}\)となります。 ここから、正面衝突が起こるまでの時間\(\Delta t_{衝突}\)と追突が起こるまでの時間\(\Delta t_{追突}\)はそれぞれ
\[\Delta t_{衝突} = \frac{\ell}{v + V} = \frac{v}{v+V} \Delta t, \quad \Delta t_{追突} = \frac{\ell}{v-V} = \frac{v}{v-V} \Delta t \tag{15}\]のように書くことができます。 (14), (15)式から、運動量の時間変化を求めてみましょう。 運動量を変化させる要因は、このミラー磁場との正面衝突と追突の過程しか存在しないとすると
\[\frac{dp}{dt} \approx \frac{\Delta p_{衝突}}{\Delta t_{衝突}} + \frac{\Delta p_{追突}}{\Delta t_{追突}} = \frac{2VE}{c^2} \frac{2V}{v \Delta t} \underbrace{=}_{(13)} 4 \left( \frac{V}{v}\right)^2 \frac{p}{\Delta t} \tag{16}\]を得ます。 さらに簡単のため、荷電粒子はすでに超相対論的速度まで加速されており、\(v \sim c\)と考えると、(16)式の解は
\[p(t) = p(0) e^{t/t_\mathrm{acc}} \qquad \left( t_\mathrm{acc} \equiv \frac{1}{4} \left(\frac{c}{V}\right)^2 \Delta t \right) \tag{17}\]のようになります。 ここで\(t_\mathrm{acc}\)は荷電粒子の加速時間です。 荷電粒子のエネルギー(運動量の大きさ)が、時間とともに指数関数的に増加していくことがわかりました。
しかし、全ての粒子がこのような加速過程をいつまでも受け続けるわけではありません。 高エネルギーに到達した荷電粒子は、磁場の乱れにより散乱されながら空間的に拡散していきます。 そしてついには銀河系から逃げていくことが予想されます。 ここでも簡単な場合として、全ての粒子は平均闘争時間\(t_\mathrm{esc}\)で逃げていくものとしましょう。 すると時刻\(t=0\)に注入された粒子が時刻\(t\)に逃げ出す確率は、拡散方程式の解から
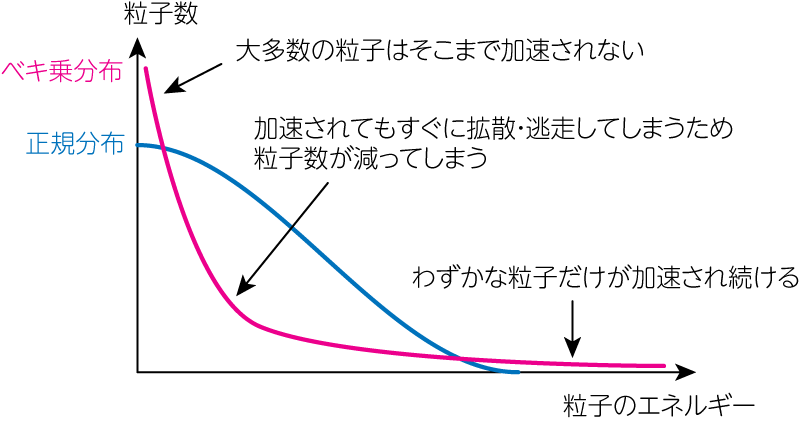
のように書くことができます。 このことから、長時間の加速を受けて高エネルギーに到達する荷電粒子の割合は、指数関数的に小さくなります。 (17), (18)式を組合せると、荷電粒子の運動量スペクトルは
\[\frac{dN}{dp} \propto \left\vert \frac{dP}{dt} \right\vert \frac{dt}{dp} \propto e^{-\frac{t}{t_\mathrm{acc}}\left( 1+ \frac{t_\mathrm{acc}}{t_\mathrm{esc}}\right)} \underbrace{\propto}_{(17)} p^{-\left( 1+\frac{t_\mathrm{acc}}{t_\mathrm{esc}}\right)} \tag{19}\]となります。 このように、このフェルミ加速がベキ型のスペクトルを与えることがわかりました。 実際の宇宙空間における高エネルギー粒子のスペクトルは、ベキ型をしていることが観測から判明しています。 大体の荷電粒子は、そこそこのエネルギーまでしか到達せずに、加速領域から拡散していきます。 指数的に小さな粒子数だけが指数的に大きなエネルギーに到達できるため、べき乗分布が形成されるのです。
実は、現実社会でも同じような現象が発生しています。 統計学で勉強するベキ分布は、労働者の収入分布をよく再現できると言われています。 指数的に少数しか存在しない”エリート”たちだけが、指数的に大きな収入を得ているという現実がここに現れています。 また地震の大きさと頻度についても、それがべき乗則に従っているとも言われています。 統計学や物理学で扱う分布といえば正規分布をイメージする方が多いと思われますが、実際に世の中に目を向けると、そこかしこに存在するのはべき乗分布であることが多いようです。
2次のフェルミ加速は全てを解決するか?
この加速機構が「2次」と呼ばれる理由は、(17)式の加速時間\(t_\mathrm{acc}\)が星間雲の速度\(V\)の2乗に依存しているためです。 ここでは、この加速機構が本当に現実の宇宙に適用できるのかを見てみましょう。 典型的な値として星間雲の速度を\(V = 10 \mathrm{km/s}\)、荷電粒子が次の衝突を起こすまでに移動する典型的な距離として\(\ell = 10 \mathrm{pc}\)とすると、 \(\Delta t \sim 10^9 \mathrm{s}\)となります。 これらの値を(17)式に代入すると
\[t_\mathrm{acc} \sim \frac{1}{4} \left( \frac{3 \times 10^{10}}{10^6}\right)^2 10^9 \sim \frac{9}{4} \times 10^{17} \ [\mathrm{s}] \sim \frac{3}{4} \times 10^{10} \ [\mathrm{yr}] \tag{20}\]のような値を得ます。 この値は宇宙年齢\(13.7 \times 10^9 \mathrm{yr}\)に近い値であることがわかります。 よってこの加速機構では、現実的には加速がほとんど起こりません。 これを解決する他の物理機構として、1次のフェルミ加速 (1st order Fermi acceleration)というものがあります。 こちらの解説記事も、(そのうち)みなさんに上納したいと考えています。
補遺: \(\mu\)が磁気モーメントであることの確認
\(\mu\)が磁気モーメントであることは、以下のようにして調べることができます。 電流\(I\)の流れる電流ループを考え、それが囲む面積を\(S\)としましょう。 すると、この系の磁気モーメントは
\[\mu = \frac{IS}{c} \tag{a1}\]で与えられます。 今、この電流ループが電荷\(q\)、速度\(v_\perp = r_L \omega_c\)でサイクロトロン運動する粒子で作られているとすると
\[I = \frac{q v_\perp}{2 \pi r_L} = \frac{q \omega_c}{2 \pi}, \quad S = \pi r_L^2 \tag{a2}\]より
\[\mu = \frac{q \omega_c r_L^2}{2c} = \frac{q v_\perp^2}{2 c\omega_c} = \frac{m v_\perp^2}{2B} = \frac{W_\perp}{B} \tag{a3}\]のように計算され、確かに磁気モーメント\(\mu\)が\(W_\perp / B\)で与えられることがわかりました。
参考文献
[1] 田中基彦, 西川恭治, “高温プラズマの物理学”
[2] Chen, 内田 岱二郎(訳), “プラズマ物理入門”
[3] 宮本健郎, “プラズマ物理・核融合”
[4] 小野高幸, 三好良純, “太陽地球圏”
[5] 加藤鞆一, “核融合はなぜむずかしいか”
[6] 高原文朗, “天体高エネルギー現象”
[7] 九州産業大学芸術学部 情報デザイン研究室, “正規分布とベキ分布”