Table of contents
レポート課題
(2.29)式から横軸を\(1/\beta J\)、縦軸を\(q\)としたグラフを描画しなさい。
(2.29)式は以下のようなものでした。
\[q = \int D_z \tanh^2 (\beta J \sqrt{q} z) \tag{R.1}\]ここではこの描画を目標に見据えつつ、段階を踏んでこのスクリプト作成の理解を深めます。
まずは準備運動
いきなり難しい問題を解くのは骨が折れるので、まずは以下の式の描画スクリプトを考えてみることにしましょう。
\[m = \tanh (\beta J m) \tag{R.2}\]これは自己無撞着方程式と呼ばれるものです。これをPythonの便利なライブラリSciPyを用いて解いてみましょう。\(a = \frac{1}{\beta J}\)とおくと、今は\(f(m) = m -\tanh (m/a)\)の解を求めることになります。
# set function
def f(x, a):
return x - np.tanh(x/a)
上述のような関数を定義しておき、これをscipy.optimize.newtonで解きます(ニュートン法の解説は省略)。あとはaについて区間[0, 2]で繰り返せば描きたいグラフを作成することができます。
以下にスクリプト全体を示します。
#!/usr/bin/env python3
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import newton
# set function
def f(x, a):
return x - np.tanh(x/a)
if __name__ == '__main__':
# set the number of divisions of a
ia = 100
# set range of a
amin = 0.0
amax = 2.0
# set a-coordinate
a_coord = np.linspace(amin, amax, ia)
m = []
m_2 = []
for a in a_coord:
# solve function
m.append(newton(f, 1.1, args=(a, )))
m_2.append(newton(f, -1.1, args=(a, )))
# make plot
plt.plot(a_coord, m)
plt.plot(a_coord, m_2)
plt.xlabel('1/βJ')
plt.ylabel('m')
# show plot
plt.show()
途中出てくるnewton(f, 1.1, args=(a, ))は、関数f(x, a)をxの初期値x0=1.1からニュートン法で求解することを意味します。最後のargs=(a, )は、関数fがx以外の引数を持つことを明示するためのものです。以上のスクリプトで作成したグラフは以下のようになります。
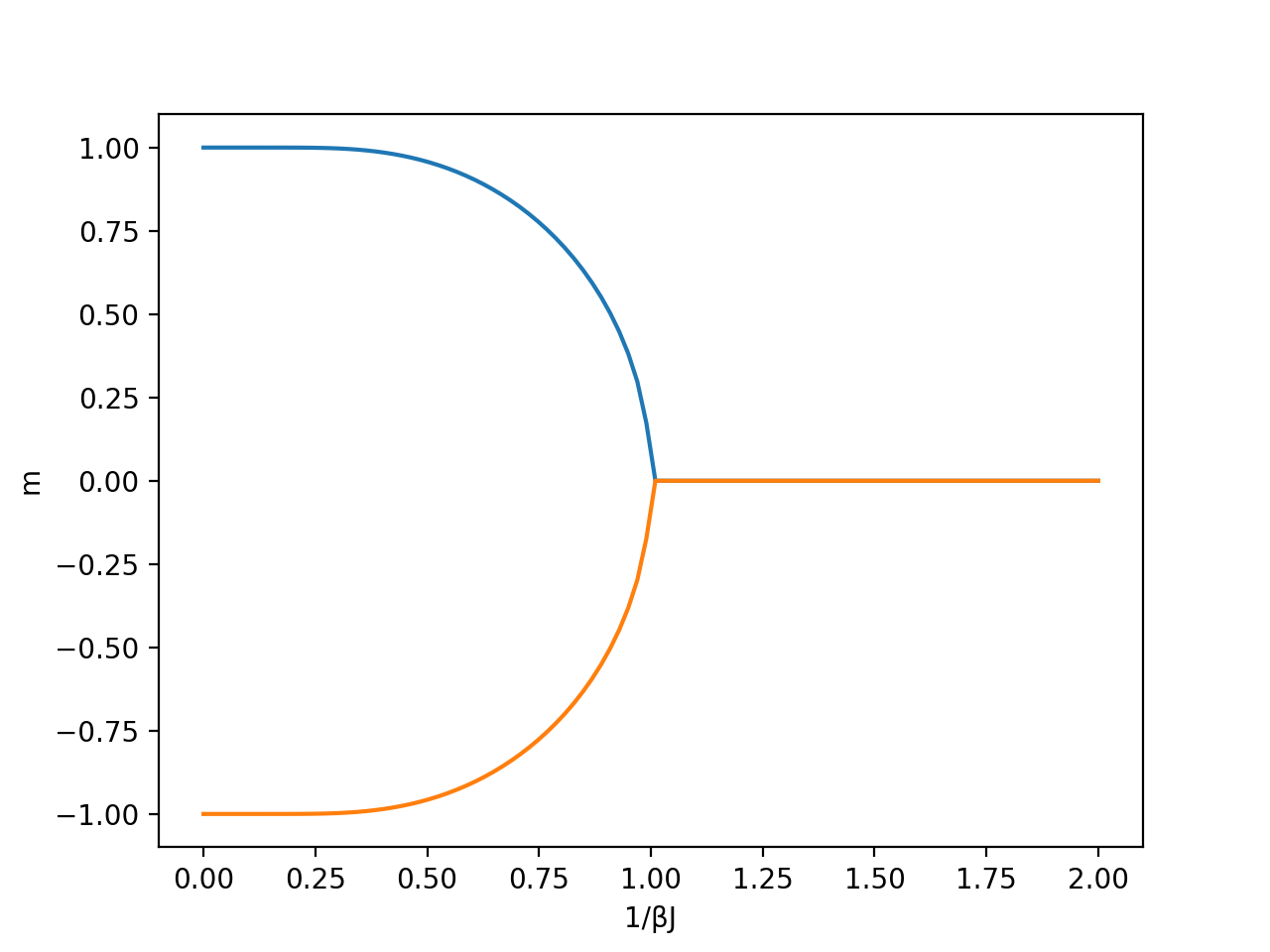
2つ曲線があるのは、ニュートン法の初期値依存性のためです。
本題
再び、描画したい方程式を見てみましょう。
\[q = \int_{-\infty}^\infty \frac{dz}{\sqrt{2\pi}} e^{-\frac{z^2}{2}} \tanh^2 (\beta J \sqrt{q} z) \tag{R.3}\]まずは右辺を数値的に積分するスクリプトを考えましょう。SciPyのintegrate.quadを用いて数値積分を行います(このアルゴリズムの説明については省略)。
# set integrand function
def integrand(z, a, q):
return np.exp(-z**2/2) * np.tanh(np.sqrt(q)/a*z) ** 2
print(quad(integrand, -10, 10, args=(a, q, )))
ここでquad(integrand, -10, 10, args=(a, q, ))は関数integrand(x, a, q)を\(-10 \leq {\rm x} \leq 10\)について数値積分することを意味します。最後のargs=(a, q, )は、関数integrandがx以外の引数を明示するためのものです。
あとは上のスクリプトでa (=\(\frac{1}{\beta J}\))と\(q\)を与えれば、右辺の積分計算を実行できたことになります。(R.3)式を描画するスクリプトは、先ほどのNewton法での求解も合わせて以下のようになります。
#!/usr/bin/env python3
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad
from scipy.optimize import newton
# set integrand function
def integrand(z, a, q):
return np.exp(-z**2/2) * np.tanh(np.sqrt(q)/a*z) ** 2
# set function
def f(q, a):
y, err = quad(integrand, -10, 10, args=(a, q, )) / np.sqrt(2*np.pi)
return q - y
if __name__ == '__main__':
# set the number of divisions of a
ia = 100
# set range of a
amin = 0.01
amax = 2.01
# set a-coordinate
a_coord = np.linspace(amin, amax, ia)
q = []
for a in a_coord:
q.append(newton(f, 1.1, args=(a, )))
# make plot
plt.plot(a_coord, q)
plt.xlabel('1/βJ')
plt.ylabel('q')
# show plot
plt.show()
このスクリプトで作成されたグラフは以下のようになります。
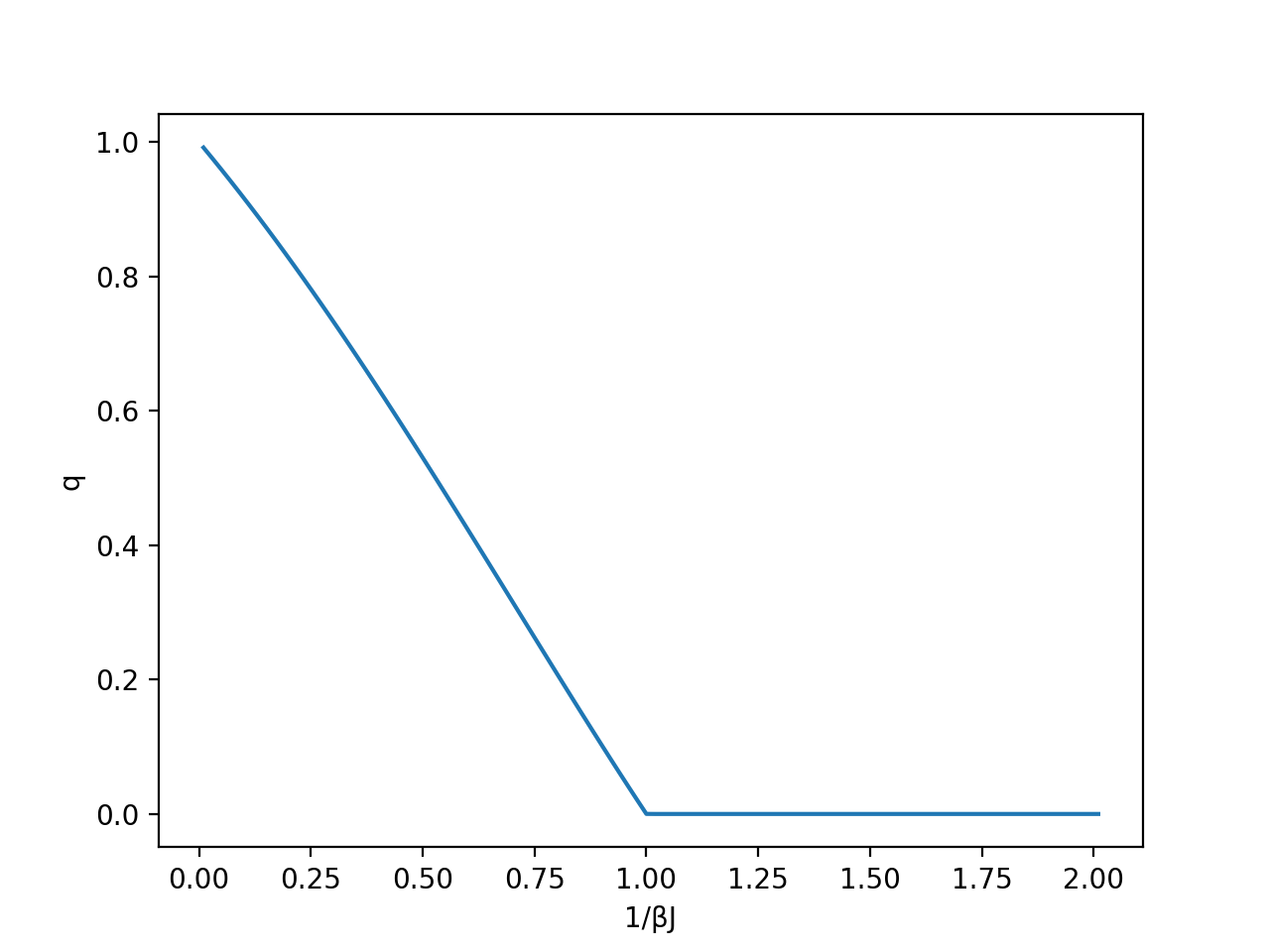
先ほどの\(m\)と違い、\(\frac{1}{\beta J} = 0\)近傍で線形な減少を示していることがわかります。
試していませんが、途中の数値積分において2重指数関数型変換を行うと積分範囲に対する収束が早くなるかもしれません。
同じ数値積分アルゴリズムでも、ロンバーグ積分(scipy.integrate.romberg)だと積分値が常に0となりました。アルゴリズムの問題?
(3.28)式で\(q \neq 0\)が解として相応しくない理由を論述しなさい
式変形から考える
(3.27)式より
\[q = \frac{q}{(\lambda - (Q - q))^2} \tag{R.3}\]\(q \neq 0\)の解を選択すると
\[1 = \frac{1}{(\lambda - (Q-q))^2} \ \Longrightarrow \ \lambda-(Q-q) = \pm 1 \ \Longrightarrow \ Q = \lambda \mp 1 + q\]この\(Q\)を用いて、固有値分布\(\rho (\lambda)\)は
\[\rho (\lambda) = \frac{1}{\pi} \mathrm{Im} (Q) = \frac{1}{\pi} \mathrm{Im} (\lambda)\]今、固有値\(\lambda\)は実数を考えているので、この式は\(\rho(\lambda) = 0\)となります。よって固有値分布が取れないことから、\(q \neq 0\)の解は不適であることがわかります。
直感的に考察する
\(q\)はスピングラス秩序パラメータであることを思い出しましょう。\(q = q^{ab} = \sum_{i=1}^N u_{i, a} u_{i,b} \ (a \neq b)\)より、\(q = 0\)は人工スピンの振る舞いが異なるレプリカごとに完全にランダムであることを意味します。それに対して\(q \neq 0\)は完全にランダムでなく、ある程度凍結を起こしている状態です。前者はランダム行列を生成するごとにバラバラな値を要素に持つ行列が生成されることに対応しますが、後者はランダム行列を何回か生成したときに同じような行列が生成されてしまうことを意味すると考えられます。よって\(q \neq 0\)はランダム行列を表現する方法としては不適切な解である、と考えることができます。