Table of contents
相対論的ビーミングによる観測される放射スペクトル変化
相対論的ビーミング効果により、磁場の周りを運動する電子は進行方向を中心とした円錐(以下、放射コーンと呼びます)内にほとんどの放射が集中します。したがって、観測者は視線方向が放射コーン内に入ったときのみ電子からの強い放射を観測すると考えて良いでしょう。よって観測者は灯台からの光のように、規則的に強いパルス電磁波を観測することになります。
観測される時間間隔
相対論的な電子が一様磁場中で円運動するときの各周波数は\(\omega_\mathrm{se} = \omega_\mathrm{ce}/\gamma\)です。そして相対論的ビーミング効果により、形成される放射コーンの角度は\(\theta \simeq 1/ \gamma\)でした。よって下図のように考えると、\(t=t_1\)のときの速度ベクトル\(\mathbf{v}_1\)と、\(t=t_2\)のときの速度ベクトル\(\mathbf{v}_2\)のなす角は\(2/\gamma\)となります。
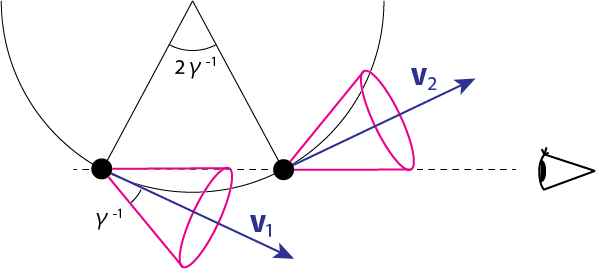
よって放射コーンが観測者の視線方向に入っている時間間隔\(\Delta t = t_2 - t_1\)は
\[\Delta t \frac{\omega_\mathrm{ce}}{\gamma} = \frac{2}{\gamma} \ \Longrightarrow \ \Delta t = \frac{2}{\omega_\mathrm{ce}} \tag{1}\]観測者は\(t_1\)に発せられた放射を\(t_1^0\)に受け取り、\(t_2\)に発せられた放射を\(t_2^0\)に受け取るとしましょう。また\(\Delta t^0 = t_2^0 - t_1^0\)です。ここで電子は大きな半径の円運動をしているとして、速度\(v\)の等速直線運動で観測者に向かってくるとします。時刻\(t_1\)での電子と観測者の距離を\(\ell\)とすると
\[t_1^0 = t_1 + \frac{\ell}{c}\] \[t_2^0 = t_2 + \frac{\ell - v \Delta t}{c}\]です。辺々を引き算すると
\[\Delta t^0 = t_2 - t_1 + \frac{\ell - v \Delta t - \ell}{c} = \Delta t + \frac{v \Delta t}{c} = \Delta t \left( 1-\frac{v}{c} \right)\]電子の速度が超相対論的であるとして、\(\gamma \gg 1, \frac{v}{c} \simeq \frac{v^2}{c^2} \sim 1\)とします。さらに(1)式より
\[\Delta t^0 \simeq \frac{1}{\gamma^2 \omega_\mathrm{ce}} \tag{2}\]となります。
観測の不確定性とスペクトル変化
観測の不確定性原理と(2)式より
\[\Delta \nu \Delta t^0 \sim 1 \ \Longrightarrow \ \Delta \nu \simeq \gamma^2 \omega_\mathrm{ce} \tag{3}\](3)式からこの電子からの電磁放射の観測スペクトルが\(0 < \nu < \gamma^2 \omega_\mathrm{ce}\)の範囲に広がります。
シンクロトロン放射の詳細な解析より
\[\nu_\mathrm{max} = 0.29 \nu_c = 0.29 \frac{3}{4\pi} \gamma^2 \omega_\mathrm{ce} \sin \alpha\]ここで\(\omega_\mathrm{ce} = \frac{eB_0}{m_e c} \simeq 17 \left( \frac{B_0}{1\mu \mathrm{G}}\right) \ s^{-1}\)です。相対論的速度を持つときの電子のエネルギーは\(E = m_e \gamma c^2\)より
\[\nu_\mathrm{max} = \frac{0.29 \times 3}{4\pi} \left( \frac{E}{m_e c^2} \right)^2 17 \left( \frac{B_0}{1\mu \mathrm{G}}\right) \sin \alpha \simeq 1.2 \left( \frac{E}{0.5 \mathrm{MeV}}\right)^2 \left( \frac{B_0}{1\mu \mathrm{G}}\right) \sin \alpha\]具体的な計算例
具体的に\(B_0 = 1\mu \mathrm{G}\)かつ\(E = 100\mathrm{TeV}\)のとき
\[\begin{align} &\nu_\mathrm{max} \simeq 1.2 \frac{(10^2 \times 10^6)^2 \mathrm{MeV}^2}{0.5^2 \mathrm{MeV}^2} \left( \frac{\sin \alpha}{1} \right) \simeq 4.8 \times 10^{16} \left( \frac{\sin \alpha}{1} \right) \ (\mathrm{s^{-1}}) \notag \\ &\Longrightarrow \ h \nu_\mathrm{max} \simeq 4.8 \times 10^{16} \cdot 2\pi \frac{\overbrace{\hbar c}^{197\mathrm{MeV \cdot fm}}}{c} \left( \frac{\sin \alpha}{1} \right) \simeq 4.8 \times 10^{16} \times 6 \frac{2 \times 10^{-11} \mathrm{MeV \cdot cm}}{3 \times 10^{10} \mathrm{cm \ s^{-1}}} \left( \frac{\sin \alpha}{1} \right) \notag \\ & \quad = 19.2 \times 10^{-5} \left( \frac{\sin \alpha}{1} \right) \ (\mathrm{MeV}) \notag \end{align}\]の周波数及びエネルギーの光子を出します。
さらに\(B_0 = 1\mu \mathrm{G}\)かつ\(E = 10 \mathrm{GeV}\)のとき
\[\begin{align} &\nu_{\rm max} \simeq 1.2 \frac{(10 \times 10^3)^2 {\rm MeV}^2}{0.5^2 {\rm MeV}^2} \left( \frac{\sin \alpha}{1} \right) \simeq 4.8 \times 10^8 \left( \frac{\sin \alpha}{1} \right) \ ({\rm s^{-1}}) \notag \\ &\Longrightarrow \ h \nu_\mathrm{max} \simeq 4.8 \times 10^8 \cdot 2\pi \frac{\overbrace{\hbar c}^{197\mathrm{MeV \cdot fm}}}{c} \left( \frac{\sin \alpha}{1} \right) \simeq 4.8 \times 10^8 \times 6 \frac{2 \times 10^{-11} \mathrm{MeV \cdot cm}}{3 \times 10^{10} \mathrm{cm \ s^{-1}}} \left( \frac{\sin \alpha}{1} \right) \notag \\ &\quad = 19.2 \times 10^{-13} \left( \frac{\sin \alpha}{1} \right) \ (\mathrm{MeV}) \notag \end{align}\]このような具体的な計算から、放射スペクトルの最大値は放射に関与している電子のエネルギーに応じて、電波からX線まで幅広い周波数範囲に及ぶことがわかります。