Table of contents

偏光のEモードとBモード

偏光のEモードとBモード

ここでは、CMB偏光などを理解する上で大切なEモード、Bモード偏光の基礎についてメモします。

Coherency matrix

\(z\)軸方向に伝播する電磁波の電場成分が

\[\begin{array}{l} E_x &= a_1 e^{i(\omega t + \delta_1)} \\ E_y &= a_2 e^{i(\omega t + \delta_2)} \end{array} \tag{1}\]

のように与えられるとしましょう。ここでは計算の都合上、複素数表示を用いています。実際の電場はこれらの実部をとったもので表されます。
ここでcoherency matrixを

\[J \equiv \left( \begin{array}{cc} E_x E_x^\ast & E_x E_y^\ast \\ E_x^\ast E_y & E_y E_y^\ast \end{array} \right) \tag{2}\]

のように定義します。これを計算しましょう。

\[\begin{array}{l} E_x^\ast &= a_1 e^{-i(\omega t + \delta_1)} \\ E_y^\ast &= a_2 e^{-i(\omega t + \delta_2)} \end{array}\]

より

\[J = \left( \begin{array}{cc} a_1^2 & a_1 a_2 e^{i(\omega t + \delta_1)-i(\omega t + \delta_2)} \\ a_1 a_2 e^{-i(\omega t + \delta_1)+i(\omega t + \delta_2)} & a_2^2 \end{array} \right) = \left( \begin{array}{cc} a_1^2 & a_1 a_2 e^{-i(\delta_2-\delta_1)} \\ a_1 a_2 e^{i(\delta_2-\delta_1)} & a_2^2 \end{array} \right)\]

ここで\(\delta \equiv \delta_2 - \delta_1\)とし、さらに式変形を進めます。

\[\begin{aligned} J &= \frac{1}{2} \left( \begin{array}{cc} a_1^2 + a_1^2 + a_2^2 - a_2^2 & 2 a_1 a_2 (\cos \delta - i \sin \delta) \\ 2 a_1 a_2 (\cos \delta + i \sin \delta) & a_2^2 + a_2^2 + a_1^2 - a_2^2 \end{array} \right) \\ &= \frac{1}{2} \left( \begin{array}{cc} a_1^2 + a_2^2 & 0 \\ 0 & a_1^2 + a_2^2 \end{array} \right) + \frac{1}{2} \left( \begin{array}{cc} a_1^2 - a_2^2 & 0 \\ 0 & -(a_1^2 - a_2^2) \end{array} \right) \\ & \qquad \qquad + \frac{1}{2} \left( \begin{array}{cc} 0 & 2 a_1 a_2 \cos \delta \\ 2 a_1 a_2 \cos \delta & 0 \end{array} \right) + \frac{1}{2} \left( \begin{array}{cc} 0 & -2 a_1 a_2 i \sin \delta \\ 2 a_1 a_2 i \sin \delta & 0 \end{array} \right) \end{aligned}\]

ここでストークスパラメータより

\[I = a_1^2 + a_2^2, \quad Q = a_1^2 - a_2^2, \quad U = 2 a_1 a_2 \cos \delta, \quad V = 2 a_1 a_2 \sin \delta \tag{3}\]

を用いると

\[J = \frac{I}{2} \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) + \frac{Q}{2} \left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array} \right) + \frac{U}{2} \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right) + \frac{V}{2} \left( \begin{array}{cc} 0 & -i \\ i & 0 \end{array} \right) \tag{4}\]

と書けます。

復習: ストークスパラメータ

ここでストークスパラメータについて復習しておきましょう。

\(\delta = 0, Q>0, U=0\)

\[U = 2 a_1 a_2 = 0\]

より\(a_1, a_2\)のどちらかが0です。さらに\(Q = a_1^2 - a_2^2 > 0\)より\(a_2=0\)とわかります。よって\(x\)方向にのみ振動するような電場となります。

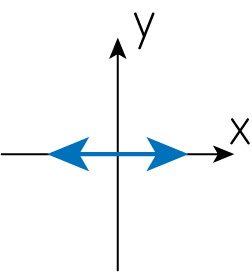
\(\delta = 0, Q<0, U=0\)

先程と同様の考え方から\(a_1=0\)とわかります。よって\(y\)方向にのみ振動するような電場となります。

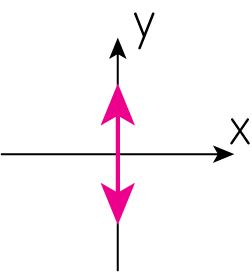
\(\delta = 0, Q=0, U>0\)

\[Q = a_1^2 - a_2^2 = 0 \ \Longrightarrow \ a_1 = \pm a_2\]

さらに\(\delta =0\)より\(U = 2a_1 a_2 > 0\)より、\(a_1 = a_2\)とわかります。よってこれは\(y=x\)上を振動するような電場です。

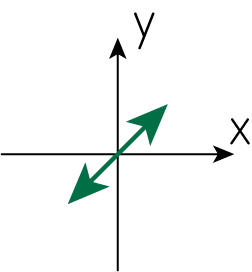
\(\delta = 0, Q=0, U<0\)

同様の考え方から\(a_1 = - a_2\)とわかります。よってこれは\(y=-x\)上を振動するような電場です。

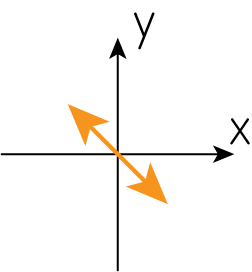
Coherency matrixのフーリエ変換

宇宙のある領域が\(\delta=0\)、すなわち\(V=0\)で直線偏光している場合を考えましょう。空の座標を\(\mathbf{x}=(x, y)\)で表すとします。偏光観測により\(I(x, y), Q(x, y), U(x, y)\)の分布が、この空の領域に対してすでに得られているとしましょう。これらを\(e^{i \mathbf{k} \cdot \mathbf{x}} \ (\mathbf{k} = (k_x, k_y))\)によりフーリエ変換した結果である\(\hat{I}(\mathbf{k}), \hat{Q} (\mathbf{k}), \hat{U} (\mathbf{k})\)を用いると、coherency matrixのフーリエスペクトルは

\[\hat{J} (\mathbf{k}) = \frac{\hat{I} (\mathbf{k})}{2} \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right) + \frac{\hat{Q} (\mathbf{k})}{2} \left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right) + \frac{\hat{U} (\mathbf{k})}{2} \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right) \tag{5}\]

のように書くことができます。波数ベクトル\(\mathbf{k}\)と\(x\)軸との成す角を\(\theta\)(\(x\)軸から\(\mathbf{k}\)へ反時計回りに正に取ります)とします。このとき座標を反時計回りに\(\theta\)回転させ、\(x\)軸と\(\mathbf{k}\)方向を一致させた新しい座標系を\((x', y')\)とします。座標変換後の\('\)系でのcoherency matrixがどのように書けるのかを示しましょう。\((x, y)\)座標系を角度\(\theta\)回転させれば良いので、回転行列\(R(\theta)\)を用いた行列の座標変換より

\[\hat{J}' (\mathbf{k}) = R(\theta) \hat{J} (\mathbf{k}) R(\theta)^{-1} = \left( \begin{array}{cc} \cos \theta & \sin \theta \\ - \sin \theta & \cos \theta \end{array} \right) \hat{J} (\mathbf{k}) \left( \begin{array}{cc} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \right)\] \[\left( \begin{array}{cc} \cos \theta & \sin \theta \\ - \sin \theta & \cos \theta \end{array} \right) \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) \left( \begin{array}{cc} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \right) = \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right)\] \[\left( \begin{array}{cc} \cos \theta & \sin \theta \\ - \sin \theta & \cos \theta \end{array} \right) \left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array} \right) \left( \begin{array}{cc} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \right) = \left( \begin{array}{cc} \cos 2\theta & -\sin 2\theta \\ -\sin 2\theta & - \cos 2\theta \end{array} \right)\] \[\left( \begin{array}{cc} \cos \theta & \sin \theta \\ - \sin \theta & \cos \theta \end{array} \right) \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right) \left( \begin{array}{cc} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \right) = \left( \begin{array}{cc} \sin 2\theta & \cos 2\theta \\ \cos 2\theta & -\sin 2\theta \end{array} \right)\]

以上より

\[\hat{J}' (\mathbf{k}) = \frac{\hat{I} (\mathbf{k})}{2} \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right) + \frac{\hat{Q} (\mathbf{k})}{2} \left( \begin{array}{cc} \cos 2\theta & -\sin 2\theta \\ - \sin 2\theta & - \cos 2\theta \end{array}\right) + \frac{\hat{U} (\mathbf{k})}{2} \left( \begin{array}{cc} \sin 2\theta & \cos 2\theta \\ \cos 2\theta & -\sin 2\theta \end{array}\right)\]

ここで

\[\hat{E} (\mathbf{k}) \equiv \hat{Q} (\mathbf{k}) \cos 2\theta + \hat{U} (\mathbf{k}) \sin 2\theta \tag{6}\] \[\hat{B} (\mathbf{k}) \equiv - \hat{Q} (\mathbf{k}) \sin 2\theta + \hat{U} (\mathbf{k}) \cos 2\theta \tag{7}\]

と定義すると

\[\hat{J}' (\mathbf{k}) = \frac{\hat{I} (\mathbf{k})}{2} \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right) + \frac{\hat{E} (\mathbf{k})}{2} \left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right) + \frac{\hat{B} (\mathbf{k})}{2} \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right) \tag{8}\]

のように書けます。

偏光のEモードとBモード

偏光状態が

\[\frac{\hat{E} (\mathbf{k})}{2} \left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right) \tag{9}\]

で表されるモードを偏光のEモードと呼びます。Eモードのみ存在するとき、すなわち\(\hat{B}=0\)のとき、(7)式と、今はすでに\(\mathbf{k}\)と\(x\)軸とが一致している座標系\(\theta=0\)にいるので

\[\hat{E} (\mathbf{k}) = \hat{Q} (\mathbf{k}), \quad \hat{U} (\mathbf{k}) = 0\]

です。これはストークスパラメータの復習部分で考えた、\(\delta = 0, Q>0, U=0\)または\(\delta = 0, Q<0, U=0\)の場合に相当します。よって\(\mathbf{k}\)との相対関係に注意して図を描くと、以下のようになります。

そして

\[\frac{\hat{B} (\mathbf{k})}{2} \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right) \tag{10}\]

で表されるモードを偏光のBモードと呼びます。同様にBモードのみ存在するとき、すなわち\(\hat{E}=0\)のとき、(6)式と、\(\theta=0\)より

\[\hat{B} (\mathbf{k}) = \hat{U} (\mathbf{k}), \quad \hat{Q} (\mathbf{k}) = 0\]

すると、これはストークスパラメータの復習部分で考えた、\(\delta = 0, Q=0, U>0\)または\(\delta = 0, Q=0, U<0\)の場合に相当します。よってこれも\(\mathbf{k}\)との相対関係に注意して図を描くと、以下のようになります。

Eモード、Bモードの逆フーリエ変換

(6)式の両辺に\(-k^2\)をかけて整理します。\(k_x = k \cos \theta, k_y = k \sin \theta\)を用いて

\[\begin{aligned} -k^2 \hat{E} (\mathbf{k}) &= -\hat{Q}(\mathbf{k}) k^2 \cos 2\theta + \hat{U}(\mathbf{k}) k^2 \sin 2\theta = -\hat{Q}(\mathbf{k}) (k^2 \cos^2 \theta - k^2 \sin^2 \theta) + \hat{U}(\mathbf{k}) 2k^2 \sin \theta \cos \theta \\ &= -\hat{Q}(\mathbf{k}) (k_x^2 - k_y^2) + \hat{U}(\mathbf{k}) 2k_x k_y \end{aligned}\]

これの逆フーリエ変換を考えましょう。そのためには以下のものを考えます。

\[\begin{aligned} &E(\mathbf{x}) = \iint_{-\infty}^\infty \hat{E} (\mathbf{k}) e^{i \mathbf{k} \cdot \mathbf{x}} d \mathbf{k} \\ &\Longrightarrow \ (\partial_x^2 + \partial_y^2) \hat{E} (\mathbf{x}) = \iint_{-\infty}^\infty \hat{E} (\mathbf{k}) \left( \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} \right) e^{i \mathbf{k}\cdot \mathbf{x}} d \mathbf{k} = \iint_{-\infty}^\infty \hat{E} (\mathbf{k}) (-k_x^2 - k_y^2) e^{i \mathbf{k}\cdot \mathbf{x}} d \mathbf{k} = \iint_{-\infty}^\infty (-k^2) \hat{E} (\mathbf{k}) e^{i \mathbf{k}\cdot \mathbf{x}} d \mathbf{k} \end{aligned}\] \[Q(\mathbf{x}) = \iint_{-\infty}^\infty \hat{Q} (\mathbf{k}) e^{i \mathbf{k} \cdot \mathbf{x}} d \mathbf{k} \ \Longrightarrow \ (\partial_x^2 - \partial_y^2) \hat{Q} (\mathbf{x}) = \iint_{-\infty}^\infty \hat{Q} (\mathbf{k}) \left( \frac{\partial^2}{\partial x^2} - \frac{\partial^2}{\partial y^2} \right) e^{i \mathbf{k}\cdot \mathbf{x}} d \mathbf{k} = \iint_{-\infty}^\infty \hat{Q} (\mathbf{k}) (-k_x^2 + k_y^2) e^{i \mathbf{k}\cdot \mathbf{x}} d \mathbf{k}\] \[U(\mathbf{x}) = \iint_{-\infty}^\infty \hat{U} (\mathbf{k}) e^{i \mathbf{k} \cdot \mathbf{x}} d \mathbf{k} \ \Longrightarrow \ 2 \partial_x \partial_y \hat{U} (\mathbf{x}) = \iint_{-\infty}^\infty \hat{U} (\mathbf{k}) 2 \frac{\partial}{\partial x} \frac{\partial}{\partial y} e^{i \mathbf{k}\cdot \mathbf{x}} d \mathbf{k} = \iint_{-\infty}^\infty \hat{U} (\mathbf{k}) (-2 k_x k_y) e^{i \mathbf{k}\cdot \mathbf{x}} d \mathbf{k}\]

以上の3式より

\[(\partial_x^2 + \partial_y^2) E(\mathbf{x}) = (\partial_x^2 - \partial_y^2) Q(\mathbf{x}) + 2 \partial_x \partial_y U(\mathbf{x}) \tag{11}\]

(7)式も同様に整理します。

\[-k^2 \hat{B}(\mathbf{k}) = \hat{Q} (\mathbf{k}) k^2 \sin 2\theta - \hat{U} (\mathbf{k}) k^2 \cos 2\theta = \hat{Q} 2 k_x k_y - \hat{U} (\mathbf{k}) (k_x^2-k_y^2)\]

先程と同様に\(\partial_x \rightarrow i k_x, \partial_y \rightarrow i k_y\)になることから

\[(\partial_x^2 + \partial_y^2) B(\mathbf{x}) = -2\partial_x \partial_y Q(\mathbf{x}) + (\partial_x^2 - \partial_y^2) U(\mathbf{x}) \tag{12}\]

\(x\)方向に伝播する単色平面波

波数が\(\mathbf{k} = (k, 0)\)の単色平面波のみ存在する場合を考えます。このときストークスパラメータは\(Q(x, y)=Q_0 \cos k x, U(x, y)=U_0 \sin kx\)、さらに\(\theta=0\)です。

\[\hat{E}(\mathbf{k}) = \hat{Q} (\mathbf{k}), \quad \hat{B}(\mathbf{k}) = \hat{U} (\mathbf{k})\]

となります。よって

\[E(\mathbf{x}) = \iint_{-\infty}^\infty \hat{E}(\mathbf{k}) e^{i \mathbf{k}\cdot \mathbf{x}} d\mathbf{k} = \iint_{-\infty}^\infty \hat{Q} (\mathbf{k}) e^{i \mathbf{k} \cdot \mathbf{x}} d \mathbf{k} = Q(\mathbf{x}) = Q_0 \cos k x\]

先述の通り、\(Q\)は\(x'\)軸(\(\mathbf{k}\)方向)に平行または垂直な偏光を司るパラメータでした。\(Q_0 >0\)とすると\(E(\mathbf{x})\)のパターンは次のようになります。

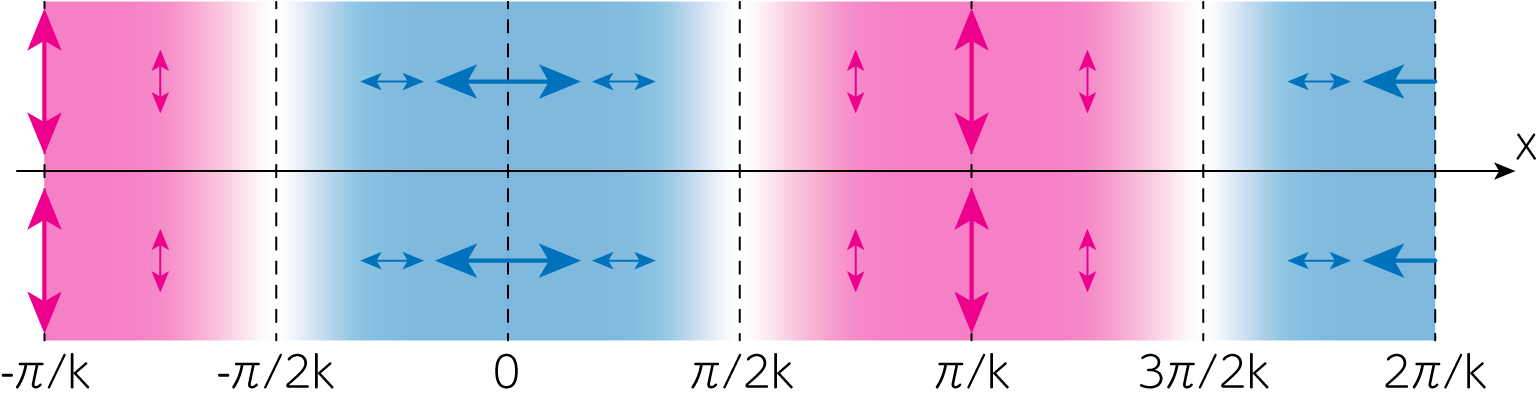
同様に

\[B(\mathbf{x}) = \iint_{-\infty}^\infty \hat{B}(\mathbf{k}) e^{i \mathbf{k}\cdot \mathbf{x}} d\mathbf{k} = \iint_{-\infty}^\infty \hat{U} (\mathbf{k}) e^{i \mathbf{k} \cdot \mathbf{x}} d \mathbf{k} = U(\mathbf{x}) = U_0 \sin k x\]

\(U\)は\(x'\)軸(\(\mathbf{k}\)方向)から\(\pi / 4\)または\(-\pi / 4\)傾いた方向の偏光を司るパラメータでした。\(U_0>0\)とすると\(B(\mathbf{x})\)のパターンは次のようになります。

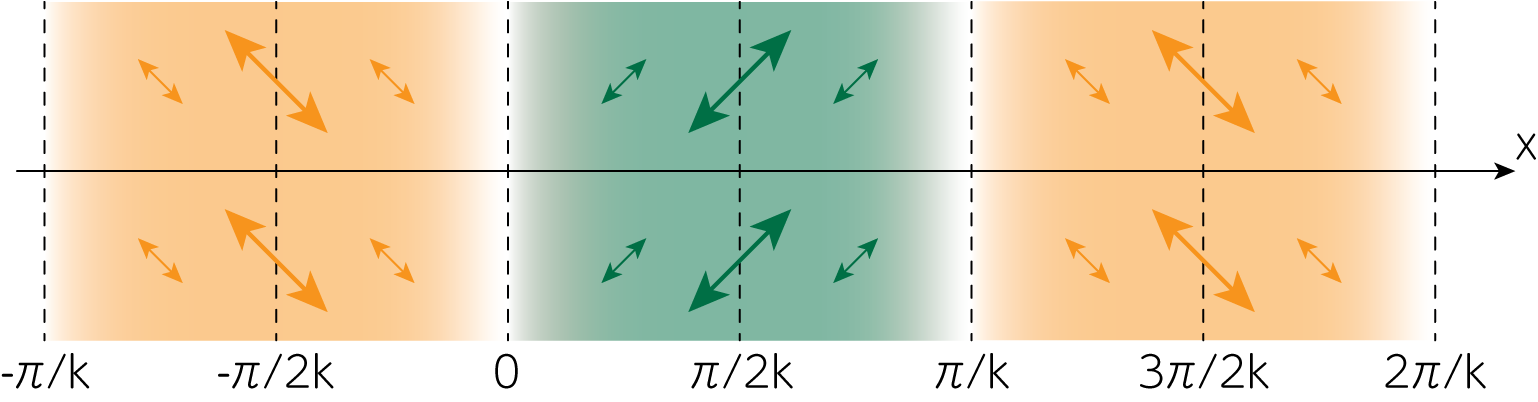
名前の由来

Eモード: 静電ポテンシャルと電場からの類推

なぜ偏光の「Eモード」と呼ぶのでしょうか。それは以下のような微分演算子

\[D_x \equiv \partial_x^2 - \partial_y^2, \quad D_y \equiv 2\partial_x \partial_y \tag{13}\]

を考え、さらにこれらの演算子を成分に持つような勾配ベクトル演算子

\[\mathbf{D} \equiv \left( \begin{array}{c} D_x \\ D_y \end{array} \right) \tag{14}\]

を定義します。さらに偏光ベクトルとして

\[\mathbf{P} \equiv \left( \begin{array}{c} Q \\ U \end{array} \right) \tag{15}\]

を定義します(\(z\)成分は以下の議論の理解を助けるためのもので、特に意味は持ちません)。
\(B(\mathbf{x})=0\)、すなわちEモードしか存在しないとき、(12)式から\(D_x U - D_y Q = 0\)です。これは先程の勾配ベクトル演算子を用いると

\[D_x U - D_y Q = (\mathbf{D} \times \mathbf{P})_z = 0\]

のように外積で表現することができます。\(\mathbf{D}, \mathbf{P}\)はどちらも\(2\)次元ベクトルなので、先程の式での\(z\)成分という制限を外しても構いません。これより

\[\mathbf{P}(B=0) \equiv \mathbf{P}_E = \mathbf{D} \Phi_E \tag{16}\]

のように偏光ベクトル\(\mathbf{P}_E\)がスカラーポテンシャル\(\Phi_E\)の勾配のように書けることがわかります。この関係式の静電場の場合との類似から、この偏光モードをEモード (electric mode)と呼びます。

Bモード: ベクトルポテンシャルと磁場からの類推

次にBモードについてです。\(E(\mathbf{x}) = 0\)でBモードしか存在しないとき

\[(\partial_x^2 - \partial_y^2) Q(\mathbf{x}) + 2\partial_X \partial_y U(\mathbf{x}) = \mathbf{D} \cdot \mathbf{P} = 0\]

と書くことができます。これより\(\mathbf{A}_B \equiv (0, 0, \Phi_B)\)を用いて

\[\mathbf{P}(E=0) \equiv \mathbf{P}_B = \mathbf{D} \times \mathbf{A}_B \tag{17}\]

のように、ベクトルポテンシャルの回転のように書けることがわかります。この関係式の磁場の場合との類似から、この偏光モードをBモード(magnetic mode)と呼びます。

\(\Phi_E = \Phi_B = r = \sqrt{x^2 + y^2}\)のとき

このようにポテンシャルが書かれているときにどのような偏光パターンが描かれるか、実際に可視化しましょう。このときの\(\Phi_E\)の微分は

\[\partial_i \Phi_E = \partial_i \sqrt{r_j r_j} = \frac{1}{2} \frac{2r_j \delta_{ij}}{\sqrt{r_j r_j}} = \frac{r_i}{r}\]

ここで\(r_i = x, y\)です。さらに計算を進めると

\[\partial_k (\partial_i \Phi_E) = \partial_k \frac{r_i}{\sqrt{r_j r_j}} = \frac{\delta_{ik} \sqrt{r_j r_j} - r_i \frac{1}{2} \frac{2r_j \delta_{jk}}{\sqrt{r_j r_j}}}{r_j r_j} = \frac{\delta_{ik}}{r} - \frac{r_i r_k}{r^3}\]

よって

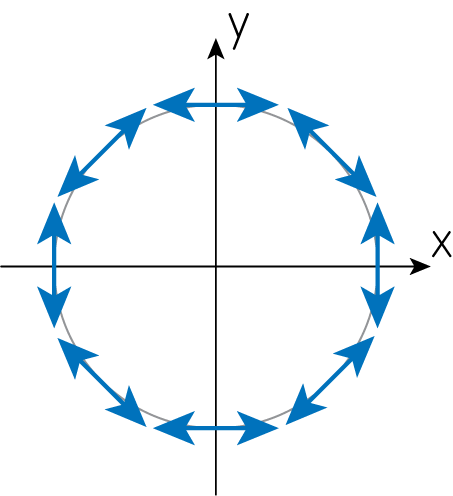
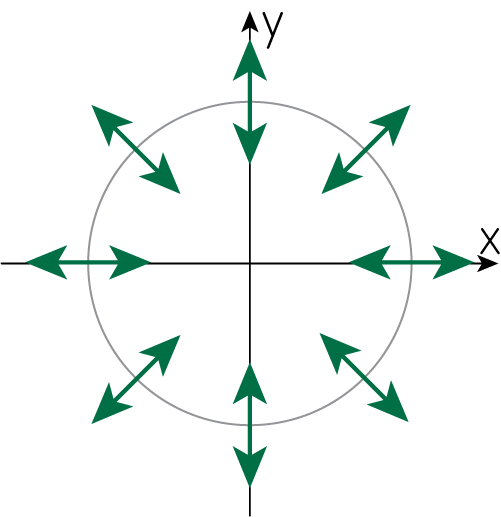
\[Q_E = P_{E, x} = D_x \Phi_E = (\partial_x^2 - \partial_y^2) r = \left( \frac{1}{r} - \frac{x^2}{r^3}\right) - \left( \frac{1}{r} - \frac{y^2}{r^3}\right) = - \frac{x^2-y^2}{r^3}\] \[U_E = P_{E, y} = D_y \Phi_E = 2 \partial_x \partial_y r = - \frac{2xy}{r^3}\]

以下ではある半径\(r\)の円上で図示することを考えましょう。まずは\(x, y\)軸上の点\((r, 0), (-r, 0), (0, r), (0, -r)\)での偏光の様子です。

(1). \((r, 0)\)では\((Q_E, U_E) = (-1/r, 0)\)のようになり、\(Q<0, U=0\)となります。ストークスパラメータの復習部分より、電磁波の偏光方向は\(x\)軸に対して垂直方向とわかります。
(2). \((-r, 0)\)では\((Q_E, U_E) = (-1/r, 0)\)のようになり、\(Q<0, U=0\)より、1番目と同じです。
(3). \((0, r)\)では\((Q_E, U_E) = (1/r, 0)\)のようになり、\(Q>0, U=0\)となります。ストークスパラメータの復習部分より、電磁波の偏光方向は\(x\)軸に対して平行方向とわかります。
(4). \((0, -r)\)では\((Q_E, U_E) = (1/r, 0)\)のようになり、\(Q<0, U=0\)より、3番目と同じです。

それ以外の場所として、先程考えた4つの間の点として考えられる、直線\(y=\pm x\)上の点\((r/\sqrt{2}, r/\sqrt{2}), (-r/\sqrt{2}, -r/\sqrt{2}), (r/\sqrt{2}, -r/\sqrt{2}), (-r/\sqrt{2}, r/\sqrt{2})\)での偏光の様子を考えましょう。すると

(5). \((r/\sqrt{2}, r/\sqrt{2})\)では\((Q_E, U_E) = (0, -1/r)\)のようになり、\(Q=0, U<0\)となります。ストークスパラメータの復習部分より、電磁波の偏光方向は\(y=-x\)に平行な方向とわかります。
(6). \((-r/\sqrt{2}, -r/\sqrt{2})\)では\((Q_E, U_E) = (0, -1/r)\)のようになり、1番目と同じです。
(7). \((r/\sqrt{2}, -r/\sqrt{2})\)では\((Q_E, U_E) = (0, 1/r)\)のようになり、\(Q=0, U>0\)となります。ストークスパラメータの復習部分より、電磁波の偏光方向は\(y=x\)に平行な方向とわかります。
(8). \((-r/\sqrt{2}, r/\sqrt{2})\)では\((Q_E, U_E) = (0, 1/r)\)のようになり、3番目と同じです。

以上の1-8番を総合すると、\(\Phi_E = r\)でのある半径上の偏光の様子は次の図のようになります。

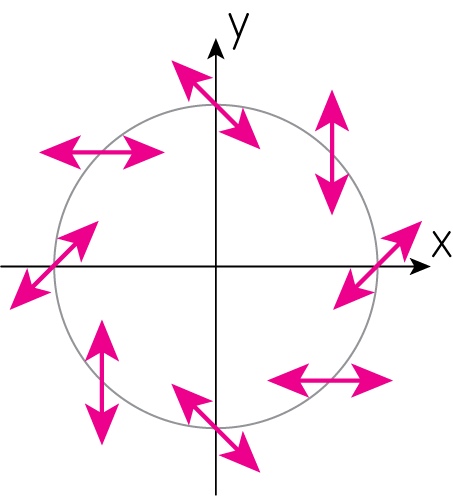
同様に考えれば、\(\Phi_B = r\)では

\[Q_B = P_{B, x} = D_y \Phi_B = - \frac{2 xy}{r^3}, \quad U_B = P_{B, y} = - D_x \Phi_B = \frac{x^2-y^2}{r^3}\]

よって、半径上の偏光の様子は次のようになります。

\(\Phi_E = \Phi_B = 1/r = 1/\sqrt{x^2 + y^2}\)のとき

最後に、この場合について実際に可視化しましょう。このときの\(\Phi_E\)の微分は

\[\partial_i \Phi_E = \partial_i \frac{1}{\sqrt{r_j r_j}} = -\frac{1}{2} (r_j r_j)^{-3/2} 2 r_j \delta_{ij} = - \frac{1}{2} \frac{r_i}{(r_j r_j)^{3/2}}\] \[\partial_k (\partial_i \Phi_E) = - \frac{\delta_{ik} (r_j r_j)^{3/2} - r_i \frac{3}{2} (r_j r_j)^{1/2} 2 r_j \delta_{jk}}{(r_j r_j)^3} = - \frac{\delta_{ik}}{(r_j r_j)^{3/2}} + \frac{3 r_i r_k}{(r_j r_j)^{5/2}}\]

よって

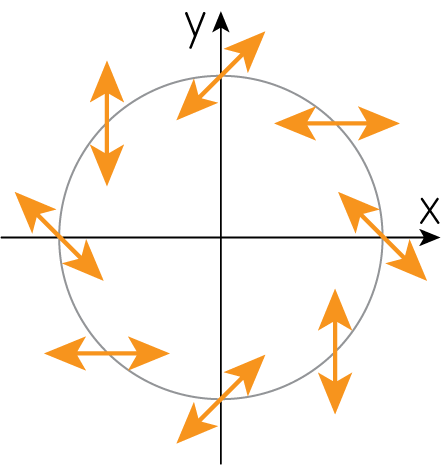
\[Q_E = P_{E, x} = D_x \Phi_E = (\partial_x^2 - \partial_y^2) \frac{1}{r} = \left( -\frac{1}{r^3} + \frac{3x^2}{r^5}\right) - \left( -\frac{1}{r^3} + \frac{3y^2}{r^5}\right) = \frac{3(x^2 - y^2)}{r^5}\] \[U_E = P_{E, y} = D_y \Phi_E = 2 \partial_x \partial_y \frac{1}{r} = \frac{6xy}{r^5}\]

先程と同様に、ある半径\(r\)の円上で図示しましょう。

(1). \((r, 0)\)では\((Q_E, U_E) = (3/r^3, 0)\)から、\(Q>0, U=0\)となります。ストークスパラメータの復習部分より、電磁場の偏光方向は\(x\)軸に対して平行方向と分かります。
(2). \((-r, 0)\)では\((Q_E, U_E) = (3/r^3, 0)\)から、\(Q>0, U=0\)となります。これは1番と同じです。
(3). \((0, r)\)では\((Q_E, U_E) = (-3/r^3, 0)\)から、\(Q<0, U=0\)となります。ストークスパラメータの復習部分より、電磁場の偏光方向は\(x\)軸に対して垂直方向と分かります。
(4). \((0, -r)\)では\((Q_E, U_E) = (-3/r^3, 0)\)から、\(Q<0, U=0\)となります。これは3番と同じです。
(5). \((r/\sqrt{2}, r/\sqrt{2})\)では\((Q_E, U_E) = (0, 3/r^3)\)のようになり、\(Q=0, U>0\)となります。ストークスパラメータの復習部分より、電磁波の偏光方向は\(y=x\)に平行な方向とわかります。
(6). \((-r/\sqrt{2}, -r/\sqrt{2})\)では\((Q_E, U_E) = (0, 3/r^3)\)のようになり、\(Q=0, U>0\)となります。これは5番と同じです。
(7). \((r/\sqrt{2}, -r/\sqrt{2})\)では\((Q_E, U_E) = (0, -3/r^3)\)のようになり、\(Q=0, U<0\)となります。ストークスパラメータの復習部分より、電磁波の偏光方向は\(y=-x\)に平行な方向とわかります。
(8). \((-r/\sqrt{2}, r/\sqrt{2})\)では\((Q_E, U_E) = (0, -3/r^3)\)のようになり、\(Q=0, U<0\)となります。これは7番と同じです。

以上の1-8番を総合すると、\(\Phi_E = 1/r\)でのある半径上の偏光の様子は次の図のようになります。

同様に考えれば、\(\Phi_B = r\)では

\[Q_B = P_{B, x} = D_y \Phi_B = \frac{6 xy}{r^5}, \quad U_B = P_{B, y} = - D_x \Phi_B = -\frac{3(x^2-y^2)}{r^5}\]

よって、半径上の偏光の様子は次のようになります。

結言

今回はCMBを理解する上で大切な要素となるEモード・Bモード偏光についてご紹介しました。Eモード・Bモードは(6), (7)式の定義から分かるように、波数空間で定義されるものです。よくある説明の仕方として「実空間で縦横の偏光はEモード、斜め方向の偏光はBモード」というような文章や図が掲載されていることがあります。しかし、それだけだと人間が見る角度を変えるだけ(今の場合首を斜めに傾けるだけ)でEモードとBモードの区別がつかなくなるため、それは説明不足である(というよりも誤り？)というのが個人的な見解です。