Table of contents

熱制動放射 (Thermal bremsstrahlung)

熱制動放射 (Thermal bremsstrahlung)

自由電子がイオンと衝突したときに、電子が運動エネルギーの一部を電磁波として放射する過程について考察しましょう。ただし、放射後も電子はイオンに束縛されず、自由電子のまま飛び去る場合に限定します。放射前後で電子は束縛されていない自由な状態であるため、これを自由-自由遷移放射 (free-free emission)と呼びます。この過程は、電子が減速(=制動)を受けることで起きる放射であることから、制動放射とも呼ばれます。 19世紀後半、レントゲン(K. Röntgen)の時代にドイツで盛んに行われていた陰極線実験の過程で発見された放射であるため、ドイツ語で制動を表すbremsと、光線の放射を表すstrahlenを合わせたブレムスシュトラールング(bremsstrahlung)とも呼ばれます。

業界の方々は、略して「ブレムス」と呼ぶらしい？

一電子からの制動放射

いきなりプラズマのような多電子・多イオンの系からの熱制動放射を考えるのは大変なので、まずは一つの電子が一つのイオンからクーロン力によるブレーキを受けた場合に発生する制動放射を考えましょう。今説明したように、プラズマ中の電子は、そのほかの電子やイオンから常にクーロン力を受けて加速度運動をしています。したがって、双極子放射による電子からの電磁波の放射が期待されます。

電子-電子相互作用

まずは電子どうしの相互作用について考えましょう。この系の電気的双極子モーメントは

\[\mathbf{d} = -e \mathbf{r}_1 - e \mathbf{r}_2 = -2 e \mathbf{R} \tag{1}\]

と計算されます。ここで\(\mathbf{r}_1, \mathbf{r}_2\)はそれぞれ、ある原点から測った2つの電子の位置です。さらに\(\mathbf{R} \equiv \frac{1}{2} (\mathbf{r}_1 + \mathbf{r}_2)\)は、この系の重心を表します。よって、この系の電気的双極子モーメント\(\mathbf{d}\)は、重心の位置\(\mathbf{R}\)に本質的に等しいことがわかります。 2つの電子がお互いにクーロン力を及ぼしあって運動している場合、作用反作用の法則から重心の加速度はゼロとなります。このことから、電子どうしの電気双極子モーメントの時間2階微分(加速度)はゼロであり、電気双極子放射は怒らないことがわかります。荷電粒子どうしの衝突による双極子放射は、異種粒子間の衝突でのみ生じることが示されました。

電子-陽子相互作用

以上の議論より、以下では電子が陽子に向かって衝突する場合を扱いましょう。この場合、電荷の大きさは同じですが、陽子の質量は電子よりも1840倍程度大きいため、同じ力を受けたときに加速度は電子の方が1840倍大きくなります。よってこの系からの放射のほとんどは電子からとなります。以下、簡単のため陽子は原点に静止しているとして考えます。陽子から電子を見た相対位置ベクトルを\(\mathbf{r}\)と書くと、この系の双極子モーメントは

\[\mathbf{d} = -e \mathbf{r} \tag{2}\]

となります。したがって、電子の運動方程式から電気双極子モーメントの時間二階微分が求まります。電子の加速度を求めるためには、電子の軌道を求めなければなりません。正確な軌道を求めるには、輻射放出が電子の運動方程式に与える影響(バックリアクション)を正確に考慮しなければなりません。しかし、その取り扱いは難しく、通常は摂動法を用いて逐次精度を上げていく方法がとられます。制動放射に関しては、観測される天体のほとんどは弱結合プラズマであるため、イオンのクーロン力が及ぼす電子軌道への影響は無視できるほど小さいと考えられます。よって衝突による散乱角も非常に小さいと近似することができます(小角度散乱, small-angle scattering。) この場合、バックリアクションを無視した取り扱いでも十分良い精度の結果を得ることができます。小角度散乱では、陽子との相互作用による電子の軌道変化も小さいため、陽子との相互作用を無視した自由電子の軌道、すなわち直線軌道と考えても差し支えないでしょう。

制動放射スペクトル分布

上述の電子-陽子相互作用において、電子が放出する電磁波のスペクトルを求めてみましょう。今、電子の運動が非相対論的であるとして、先程の双極子近似が良い精度で成り立つとします。すると双極子の振動の周波数と同じ周波数の電磁波が放射されます。双極子モーメントをフーリエ積分表示すると

\[\mathbf{d} = \int_{-\infty}^\infty \hat{\mathbf{d}}(\omega) e^{-i\omega t} d\omega \ \Longrightarrow \ \ddot{\mathbf{d}} = \int_{-\infty}^\infty \hat{\mathbf{d}} (\omega) (-\omega^2) e^{-i \omega t} d\omega \underbrace{=}_{(2)} - e \ddot{\mathbf{r}} = -e \dot{\mathbf{v}} \tag{3}\]

となります。ここで、電子の速度を\(\mathbf{v} = \dot{\mathbf{r}}\)としました。この両辺をフーリエ変換すれば

\[- \omega^2 \hat{\mathbf{d}}(\omega) = -\frac{e}{2\pi} \int_{-\infty}^\infty \dot{\mathbf{v}} e^{i\omega t} dt \ \Longrightarrow \ \hat{\mathbf{d}}(\omega) = \frac{e}{2\pi \omega^2} \int_{-\infty}^\infty \dot{\mathbf{v}} e^{i\omega t} dt \tag{4}\]

と求まります。

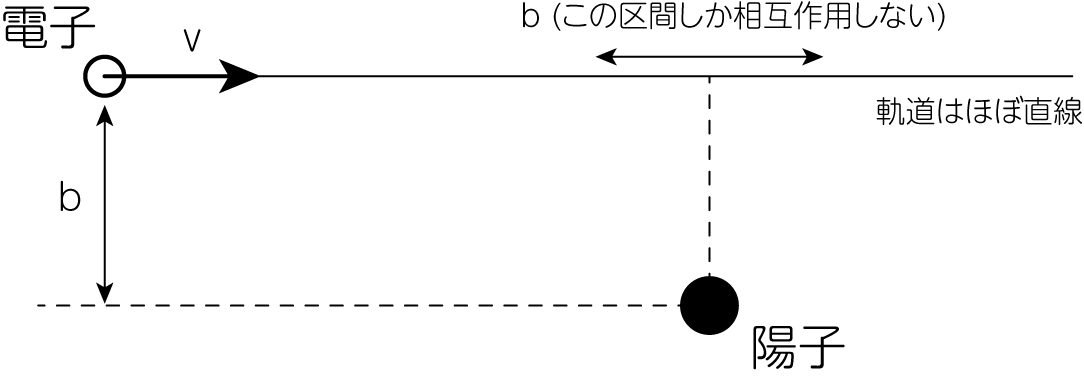
衝突パラメータを\(b\)とし、ここから、衝突時間を\(\tau = b/v\)のように定めましょう。これは電子が陽子のクーロン力の影響を強く受けて加速度運動している期間は、最も陽子に近づいた地点を中心として、衝突パラメータ程度の距離を運動している間であることを意味します。したがって、\(\tau\)を「電子とイオンの衝突(イオンからのクーロン力による電子の減速)が起きている時間間隔」と考えるたためです。以下では簡単のため、電子はこの衝突時間\(\tau\)の間に一定の加速度を受け、それ以外では加速度は受けないと近似します。この仮定から、（4)式の積分は

\[\int_{-\infty}^\infty \dot{\mathbf{v}} e^{i\omega t} = \dot{\mathbf{v}} \int_{-\tau / 2}^{\tau / 2} e^{i\omega t} dt = \dot{\mathbf{v}} \tau \mathrm{sinc} \frac{\omega \tau}{2} \underbrace{=}_{\dot{\mathbf{v}} = \frac{\Delta \mathbf{v}}{\tau}} \Delta \mathbf{v} \mathrm{sinc} \frac{\omega \tau}{2} \tag{5}\]

のように計算されます。ここで\(\Delta \mathbf{v}\)は、陽子による散乱の前後での電子の速度ベクトルの変化量です。双極子モーメントはsinc関数の性質から、以下のように近似できます。

\[\hat{\mathbf{d}} (\omega) \simeq \left\{ \begin{array}{ll} \frac{e}{2\pi \omega^2} \Delta \mathbf{v} & \omega \tau \ll 1 \\ 0 & \omega \tau \gg 1 \end{array} \right. \tag{6}\]

この結果を非相対論的極限から導かれる単位周波数あたりの全放射エネルギー(39)式に代入することで、非相対論的電子からの制動放射の単位周波数あたりのエネルギー放射強度が求まります。

\[\frac{dW}{d\omega} = \left\{ \begin{array}{ll} \frac{2e^2}{3\pi c^3} \vert \Delta \mathbf{v} \vert^2 & \omega \tau \ll 1 \\ 0 & \omega \tau \gg 1 \end{array} \right. \tag{7}\]

今、小角度散乱を考えているため、軌道に沿った方向の速度は陽子のそばを通り過ぎる前と通り過ぎた後で打ち消しあうと考えられます。よって、結局は速度の変化は軌道と垂直方向にのみ起こると仮定しても差し支えないでしょう。

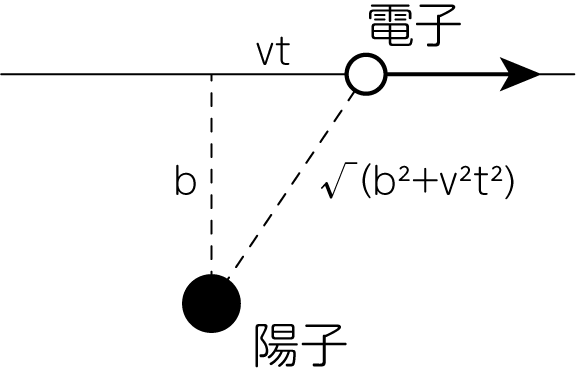
上図のような座標系で考えると、軌道に垂直な方向の電子の運動方程式は

\[m_e \frac{dv_\perp}{dt} = \frac{e^2}{b^2 + v^2 t^2} \underbrace{\frac{b}{\sqrt{b^2 + v^2 t^2}}}_{垂直方向への射影} \tag{8}\]

のようになります。

(8)式を時間で積分することで、\(\Delta \mathbf{v} = (0, \Delta v)\)が求まります。

\[\Delta v = \frac{e^2}{m_e} \int_{-\infty}^\infty \frac{b dt}{(b^2 + v^2 t^2)^{3/2}} \underbrace{=}_{vt = b \tan \theta} \frac{e^2}{m_e vb} \int_{-\pi/2}^{\pi/2} \cos \theta d \theta = \frac{2e^2}{m_e v b} \tag{9}\]

これを(7)式に代入すれば

\[\frac{dW(b)}{d\omega} = \left\{ \begin{array}{ll} \frac{8e^6}{3\pi c^3 m_e^2 v^2 b^2} & \omega \tau \ll 1 \\ 0 & \omega \tau \gg 1 \end{array} \right. \tag{10}\]

のように、制動放射のスペクトル分布を求めることができました。

プラズマからの制動放射

ここまでの結果を用いて、電子密度\(n_e\)、陽子密度\(n_p\)からなるプラズマからの制動放射を計算しましょう。プラズマには電荷中性が破れると直ちに復元力が働いて電荷分布の中性を保とうとする性質があるのでした。この性質より、\(n_e = n_p\)が良い近似で成立しているはずです。ここである一つの陽子に注目して、それを中心にした半径\(b \sim b+db\)の円環を考えましょう。プラズマ中の電子群が、全て速度\(v\)でこの円環に垂直に入射したとすると、この円環を単位時間あたりに通過する電子の数は\(n_e v 2\pi b db\)となります。一方、単位体積あたりのターゲット陽子数は\(n_p\)です。制動放射が観測される天体ではほとんどの場合、放出される電磁波の波長(例えば10Å程度)が、電子間距離(例えば銀河団では10cm程度)に比べて圧倒的に短いことが知られています。よって、異なる電子からの放射は非可干渉な重ね合わせと考えて大丈夫でしょう。すると、この円環を突っ切る電子からの制動放射スペクトルは

\[2\pi v n_e n_p b \frac{dW}{d\omega} db \tag{11}\]

のように書かれます。これを\(b\)が取りうる範囲\([b_\mathrm{min}, b_\mathrm{max}]\)で積分することで、このプラズマからの単位体積・単位角周波数あたりの熱制動放射の放射強度を得ます。

\[\frac{dW}{d\omega dV dt} = 2\pi v n_e n_p \int_{b_\mathrm{min}}^{b_\mathrm{max}} \frac{dW(b)}{dw} b db = \frac{16 e^6}{3 c^3 m_e^2 v} n_e n_p \ln \left( \frac{b_\mathrm{max}}{b_\mathrm{min}}\right) \tag{12}\]

ここでの積分結果は\(\omega \tau \ll 1 \ \Longrightarrow \omega \ll v/b\)のような、低周波数極限の結果のみを示しました。そこで、\(b_\mathrm{max} = v/\omega\)を衝突パラメータの最大値として利用しましょう。さらに、ここまでの式は小角度散乱の仮定を用いて導出していたのでした。よって、散乱角が90°以下であることを小角度散乱の条件として採用しましょう。クーロンポテンシャルエネルギーが運動エネルギーに比べて小さければ、電子の運動はあまり影響を受けずに小角度散乱となると言えるので

\[\frac{e^2}{b} \leq m_e v^2 \ \Longrightarrow \ b \geq \frac{m_e v^2}{e^2} = b_\mathrm{min} \tag{13}\]

のように\(b_\mathrm{min}\)を計算することができます。実際には\(b \sim b_\mathrm{min}, b \sim b_\mathrm{max}\)では、低周波極限や小角度散乱の近似精度は良くないでしょう。このことからもわかるように、衝突パラメータの最大値・最小値を決めることには不定性が大きいことがわかります。しかし(12)式を見ると、これらは対数の中に入っているため、不定性による誤差は些細なものとなります。ここで採用した\(b_\mathrm{min}, b_\mathrm{max}\)の計算はあくまで一つの例であり、対象としているプラズマの状態によっては、異なる物理を考慮する必要があります。 (12)式の最後の対数部分をクーロン対数(Coulomb logarism)と呼びます。さらに対数部分を取り出し、以下の量をガウントファクター(Gaunt factor)と呼びます。

\[g_{ff} (v, \omega) = \frac{\sqrt{3}}{\pi} \ln \left( \frac{b_\mathrm{max}}{b_\mathrm{min}}\right) \tag{14}\]

これはオーダー1程度の量であり、詳細な値はこれを専門に扱っているプロフェッショナルたちの計算結果のテーブルを用いることが常套手段です。ガウントファクターを用いて制動放射スペクトルを記述すると

\[\frac{dW (v, \omega)}{d\omega dV dt} = \frac{16 \pi e^6}{3\sqrt{3} c^3 m_e^2 v} n_e^2 g_{ff} (v, \omega) \tag{15}\]

のようになります。最後に完全電離水素ガスのプラズマとして、\(n_e = n_p\)のようにしました。

熱制動放射

ここまでは、全ての電子の速度はある一つの値で一定として計算を行なってきました。実際のプラズマでは、電子の速度はある分布に従って運動を行なっています。よって、プラズマからの制動放射のスペクトルを求めたければ、ここまで得られた結果を電子の速度で平均したものを計算する必要があるでしょう。ここでは熱平衡にあるプラズマを取り扱い、プラズマ中の電子の速度がマクスウェル・ボルツマン分布に従うとします。このようにして求められた制動放射を、特に熱制動放射(thermal bremsstrahlunb)と呼びます。 \(\mathbf{v} \sim \mathbf{v} + d \mathbf{v}\)の速度の電子が見つかる確率を\(P(\mathbf{v})\)とすると

\[P(\mathbf{v}) = \left( \frac{m_e}{2\pi k_B T}\right)^{3/2} e^{-m_e v^2 / 2k_B T} \tag{16}\]

のように書かれるのでした。この速度分布で重みづけをして平均操作を行います。ここで、速度の取りうる範囲に量子力学的な効果からの制限が存在します。制動放射では、電子の運動エネルギーの一部が電磁波のエネルギーとして放射されます。量子力学によると、振動数\(\nu\)の電磁波はエネルギー\(h\nu\)の光子と考えることができます。よって、振動数\(\nu\)の電磁波を放射するには、エネルギー\(h\nu\)の光子を少なくとも一つは放出しなければなりません。放射後も電子が陽子に束縛されずに自由電子でいるためには、放射前の電子の運動エネルギーが\(h\nu\)を超えている必要があるでしょう。よって

\[h\nu \leq \frac{1}{2} m_e v^2 \ \Longrightarrow \ v \geq \sqrt{\frac{2h\nu}{m_e}} \equiv v_\mathrm{min} \tag{17}\]

のように速度の下限が求まります。最後に、ガウントファクターを速度について平均した\(\tilde{g}_{ff} (\omega)\)で置き換えて計算しましょう。これは、ガウントファクターの速度依存性の小ささから行える近似です。以上から、制動放射スペクトルを電子の速度分布について平均を取る計算を行うことができます。 \(2\pi d\nu = d\omega\)より

\[\frac{dW (T, \nu)}{d\nu dV dt} = 2\pi \frac{\int_{v_\mathrm{min}}^\infty v^2 e^{-m_e v^2 / 2k_B T} \frac{dW(v, \omega)}{d\omega dV dt} dv}{\int_{v_0}^\infty v^2 e^{-m_e v^2 / 2k_B T}dv} \tag{18}\]

ガウス積分公式の派生系より

\[\int_0^\infty v^2 e^{-m_e v^2 / 2k_B T} dv = \frac{1}{4} \sqrt{\left( \frac{2k_B T}{m_e}\right)^3 \pi} \tag{19}\]

と計算されるので

\[\begin{align} \frac{dW}{d\nu dV dt} &= 8\pi \sqrt{\frac{m_e^3}{8 \pi k_B^3 T^3}} \frac{16\pi e^6}{3\sqrt{3} c^3 m_e^2} n_e^2 \tilde{g}_{ff} (\omega) \int_{v_\mathrm{min}}^\infty v e^{-m_e v^2 / 2k_B T} dv \notag \\ &= \frac{4\pi m_e}{k_B T} \sqrt{\frac{m_e}{2\pi k_B T}} \frac{16 \pi e^6}{3\sqrt{3} c^3 m_e^2} n_e^2 \tilde{g}_{ff} (\omega) \left[ -\frac{k_B T}{m_e} e^{-m_e v^2 / 2k_B T}\right]_{v_\mathrm{min}}^\infty \notag \\ &\underbrace{=}_{(17)} \frac{2^5 \pi e^6}{3 c^3 m_e} \sqrt{\frac{2\pi}{3m_e k_B}} n_e^2 T^{-1/2} \tilde{g}_{ff} (\omega) e^{-h\nu / k_B T} \tag{20} \end{align}\]

のように計算されます。ここでも、異なる電子からの放射が非可干渉な重ね合わせで良いことを用いています。
(20)式から、高温プラズマからの熱制動放射のスペクトルについて、次のような特徴がわかります。 \(e^{-h\nu / k_B T}\)の因子のために、\(h\nu > k_B T\)となる高周波領域では、熱制動放射強度が急激に減少します。これは\(k_B T\)のエネルギーを超える光子を放射するには、当然ですが電子の運動エネルギーが\(k_B T\)を超えている必要があるためです。これは熱平衡(マクスウェル・ボルツマン)分布では、高いエネルギーの電子数が指数的に減少することに起因します(下図左パネル。)

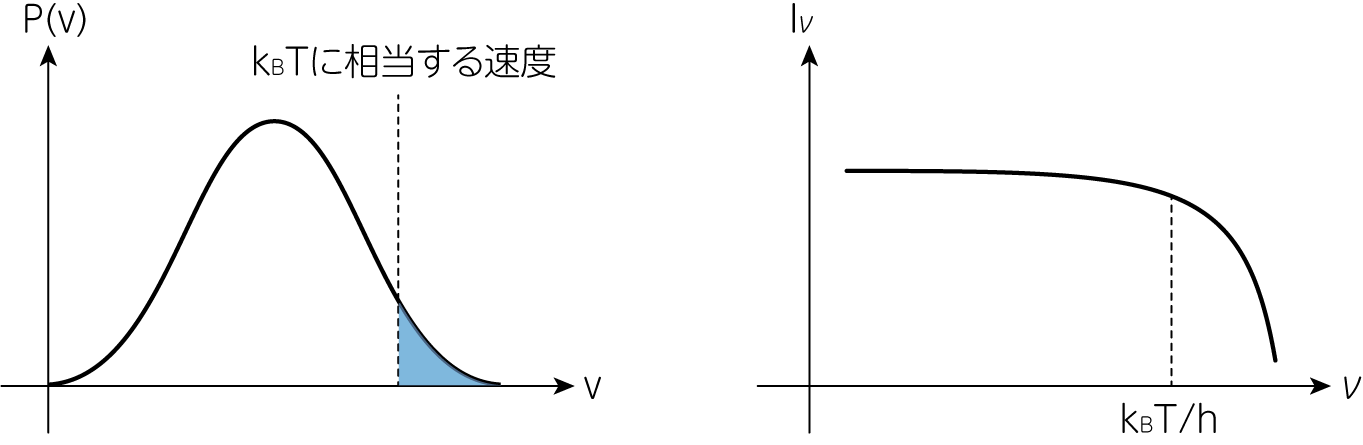
さらに\(h\nu \ll k_B T\)の低周波領域では、強度は周波数に依存せず一定となります。さらにこの強度は電子数密度の2乗に比例します。これは制動放射が電子とイオンの衝突過程で放射されるためであり、衝突の確率が電子・イオンの数密度の席に比例するためです。最後に、放射強度の温度に対する依存性は弱く、温度の平方根に逆比例します。これらの特徴から、天体からの熱制動放射スペクトルの周波数が測定できれば

スペクトルが急激に減少する周波数から、プラズマの温度が推定できる（上図右パネル）
強度の絶対値から、電子数密度の推定ができる

などの利点があります。

放射率 (emissivity) と全輝度 (bolometric luminosity)

(20)式で与えられる単位周波数・単位体積・単位時間あたりの放射強度を制動放射の放射率(emissivity)と呼び、\(\epsilon_\nu^{ff}\)と定義します。このとき、(20)式の係数部分を詳細に計算し、どの程度の大きさなのかを見積もってみましょう。

\[\begin{align} \frac{2^5 \pi e^6}{3 c^3 m_e} \sqrt{\frac{2\pi}{3 m_e}} &= \frac{2^{11/2} \pi^{3/2}}{3^{3/2}} \left\{ \frac{e^2}{\hbar c} (\hbar c) \right\}^3 \frac{1}{(m_e c^2)^{3/2}} \sim \frac{2^{11/2} \pi^{3/2}}{3^{3/2}} \left( \frac{200 \mathrm{MeV \cdot fm}}{140}\right)^3 \frac{1}{(0.5 \mathrm{MeV})^{3/2}} \notag \\ &\sim \frac{2^{11/2} \pi^{3/2}}{3^{3/2}} \frac{10^3}{7^3} 1 \mathrm{MeV}^{3/2} \cdot 1\mathrm{fm}^3 \cdot 2^{3/2} \tag{21} \end{align}\]

これと、(20)式において温度と電子数密度を\(k_B T = 10 \mathrm{keV}, n_e = 10^{-3} \mathrm{cm}^{-3}\)のように典型的な銀河団プラズマの値で規格化すれば

\[\begin{align} \epsilon_\nu^{ff} &\simeq \frac{2^7 \pi^{3/2}}{3^{3/2}} \frac{10^3}{7^3} 1 \mathrm{MeV}^{3/2} \cdot 1 \mathrm{fm}^3 \times 10^{-6} \left( \frac{n_e}{10^{-3} \mathrm{cm}^{-3}}\right)^{2} \times (10^{-2} \mathrm{MeV})^{-1/2} \left(\frac{k_B T}{10 \mathrm{keV}} \right)^{-1/2} \tilde{g}_{ff} e^{-h\nu/k_B T} \notag \\ &\simeq \frac{2^7 \cdot 10^{-2} \pi^{3/2}}{3^{3/2} \cdot 7^3} 1 \mathrm{MeV} \cdot 1 \mathrm{fm}^3 \left( \frac{n_e}{10^{-3} \mathrm{cm}^{-3}}\right)^{2} \left(\frac{k_B T}{10 \mathrm{keV}} \right)^{-1/2} \tilde{g}_{ff} e^{-h\nu/k_B T} \notag \\ &\simeq \frac{2^7 \cdot 10^{-2} \pi^{3/2}}{3^{3/2} \cdot 7^3} (10^6 \times 1.6 \times 10^{-12}) \cdot (10^{-13})^3 \left( \frac{n_e}{10^{-3} \mathrm{cm}^{-3}}\right)^{2} \left(\frac{k_B T}{10 \mathrm{keV}} \right)^{-1/2} \tilde{g}_{ff} e^{-h\nu/k_B T} \notag \\ &\simeq \frac{2^11 \pi^{3/2}}{3^{3/2} \cdot 7^3} \times 10^{-48} \left( \frac{n_e}{10^{-3} \mathrm{cm}^{-3}}\right)^{2} \left(\frac{k_B T}{10 \mathrm{keV}} \right)^{-1/2} \tilde{g}_{ff} e^{-h\nu/k_B T} \notag \\ &\simeq 6.4 \times 10^{-48} \left( \frac{n_e}{10^{-3} \mathrm{cm}^{-3}}\right)^{2} \left(\frac{k_B T}{10 \mathrm{keV}} \right)^{-1/2} \tilde{g}_{ff} e^{-h\nu/k_B T} \ [\mathrm{erg \cdot s^{-1} \cdot \mathrm{Hz}^{-1} \cdot cm^{-3}}] \tag{22} \end{align}\]

のようになります。

もう少し厳密に計算すると、係数は6.3程度となります。

これを全周波数と放射を出している全領域体積で積分しましょう。このとき、観測している天体は電子数密度と温度が一様な天体であるとすると

\[\begin{align} L &\equiv \frac{dW}{dt} = \int dV \int_0^\infty d\nu \epsilon_\nu^{ff} \notag \\ &= 6.4 \times 10^{-48} \left( \frac{n_e}{10^{-3} \mathrm{cm}^{-3}}\right)^{2} \left(\frac{k_B T}{10 \mathrm{keV}} \right)^{-1/2} \tilde{g}_{ff} V \int_0^\infty e^{-h\nu/k_B T} d\nu \notag \\ &= 6.4 \times 10^{-48} \left( \frac{n_e}{10^{-3} \mathrm{cm}^{-3}}\right)^{2} \left(\frac{k_B T}{10 \mathrm{keV}} \right)^{-1/2} \tilde{g}_{ff} V \frac{k_B T}{h} \tag{23} \end{align}\]

のように簡単に計算することができます。ここで体積\(V\)を典型的な銀河団の大きさ、すなわち半径1Mpcの球形であるとしましょう。

\[V = \left( \frac{V}{\frac{4\pi}{3} (1\mathrm{Mpc})^3} \right) \frac{4\pi}{3} (1\mathrm{Mpc})^3 \simeq 4\pi \times 3^2 \times 10^{72} \left( \frac{V}{\frac{4\pi}{3} (1\mathrm{Mpc})^3} \right) \tag{24}\]

そして積分からもう一つ\(k_B T\)が出現したので

\[\left(\frac{k_B T}{10 \mathrm{keV}} \right)^{-1/2} k_B T = \left( \frac{k_B T}{10 \mathrm{keV}} \right)^{1/2} 10 \mathrm{keV} \simeq 1.6 \times 10^{-8} \left( \frac{k_B T}{10 \mathrm{keV}} \right)^{1/2} \tag{25}\]

のように計算し、最後にプランク定数\(h = 6.6 \times 10^{-27} \ [\mathrm{erg \cdot s}]\)を用いれば

\[\begin{align} L &\simeq \frac{6.4 \times 1.6 \times 4\pi \times 3^2}{6.6} \times 10^{43} \left( \frac{n_e}{10^{-3} \mathrm{cm}^{-3}}\right)^{2} \left(\frac{k_B T}{10 \mathrm{keV}} \right)^{1/2} \left( \frac{V}{\frac{4\pi}{3} (1\mathrm{Mpc})^3} \right) \tilde{g}_{ff} \notag \\ &\simeq 1.7 \times 10^{45} \left( \frac{n_e}{10^{-3} \mathrm{cm}^{-3}}\right)^{2} \left(\frac{k_B T}{10 \mathrm{keV}} \right)^{1/2} \left( \frac{V}{\frac{4\pi}{3} (1\mathrm{Mpc})^3} \right) \tilde{g}_{ff} \ [\mathrm{erg \cdot s^{-1}}] \tag{26} \end{align}\]

のように求まります。これを熱制動放射の全輝度(bolometric luminosity)と呼びます。電子数密度の2乗、そして温度のルートに比例するのは、衝突頻度が\(v n_e n_p (\propto T^{-1/2}n_e^2)\)に比例することからくるものです。

実際の銀河団プラズマ観測

宇宙に存在する銀河団プラズマが熱制動放射で観測されるとき、実際にはどのように見えるでしょうか。まずは偏光状態について考えてみましょう。制動放射の原理を見てみると、電子はその軌道を少し曲げることにより放射を出します。従って、この放射は下図のように、縦に振動する直線偏光電磁波として観測されます。

しかし、銀河団プラズマのように多数の電子からなる系を見てみると、電子の運動方向はみなランダムであると考えることができます。ここから、銀河団プラズマを観測した場合には、これらが全て重ね合わさったものとして観測されるため、結局は無偏光状態として観測されるとわかります。

ここまでの議論は、実は光学的に薄いことを仮定しています。もし光学的に厚ければ、奥側から出た制動放射は途中のプラズマ粒子に散乱され、そのスペクトルが変化するはずです。よって、まずは銀河団が光学的に薄いことを示してみましょう。トムソン散乱の散乱断面積より、光学的厚み\(\tau\)は

\[\tau = \sigma_T n_e \ell = \frac{8\pi}{3} \left( \frac{e^2}{m_e c^2}\right)^2 n_e \ell \simeq n_e \ell \cdot \frac{2}{3} \mathrm{barn} \simeq n_e \ell \cdot \frac{2}{3} \times 10^{-24} \mathrm{cm}^2 \tag{27}\]

のように計算されます。ここに銀河団プラズマの典型的な値である\(n_e \sim 10^{-3} \mathrm{cm}^{-3}, \ell = 1 \mathrm{Mpc} \sim 3 \times 10^{24} \mathrm{cm}\)を代入すると

\[\tau \sim 2 \times 10^{-3} \ll 1 \tag{28}\]

と求まります。よって銀河団は光学的に薄いことがわかりました。ここから、銀河団プラズマを観測するときには、散乱を気にすることなく熱制動放射を観測できることがわかります。実際に面積\(1 \mathrm{cm}^2\)の検出器を用意したときに、単位時間あたりに半径1Mpc, 電子数密度\(n_e \sim 1 \mathrm{cm}^{-3}\), 温度\(k_B T \sim 10 \mathrm{keV}\)の銀河団から到来する1keV以上のエネルギーを持った光子数を求めてみましょう。ただし銀河団までの距離を\(R\)、そして簡単のために\(\tilde{g}_{ff} \sim 1\)とします。 (22)式より、\(\epsilon_\nu^{ff}\)は単位時間・単位体積・単位周波数あたりに熱制動放射により放出される電磁波のエネルギーです。これを光子一個あたりのエネルギー\(h\nu\)で割ることで、単位時間・単位体積・単位周波数あたりに放出される光子数に変換することができます。

\[\frac{\epsilon_\nu^{ff}}{h \nu} = \frac{6.4 \times 10^{-48}}{h\nu} e^{-h\nu / 10 \mathrm{keV}} \tag{29}\]

これを\(1 \mathrm{keV}/h \sim \infty\)の周波数で積分することで、単位時間・単位体積あたりに放出される1keV以上のエネルギーを持つ光子数を求めましょう。

\[n = \int_{1\mathrm{keV} / h}^\infty n d\nu = \frac{6.4 \times 10^{-48}}{h} \int_{1\mathrm{keV} / h}^\infty \frac{d\nu}{\nu} e^{-h\nu / 10 \mathrm{keV}} \underbrace{=}_{\frac{h\nu}{10 \mathrm{keV}} = x} \frac{6.4 \times 10^{-48}}{h} \int_{0.1}^\infty \frac{e^{-x}}{x} dx \tag{30}\]

最後の積分部分は第一exponential integralと呼ばれるものです。数表や数値積分結果から\(\int_{0.1}^\infty e^{-x}/x \sim 1.82\)という値を拝借しましょう。すると銀河団から距離\(R\)にある検出器に、単位時間あたりにやってくる光子数は

\[\frac{\frac{4\pi}{3} (1 \mathrm{Mpc})^3 n}{4\pi R^2} \simeq \frac{(3 \times 10^{24})^3}{3 R^2} \frac{6.4 \times 10^{-48}}{6.6 \times 10^{-27}} \times 1.82 \simeq \frac{1.7 \times 10^{52}}{R^2} \ [\mathrm{s}^{-1}] \tag{31}\]

のように求まります。ちなみに、この検出器に単位時間あたりに1個の光子が届くような距離は

\[R \sim \sqrt{1.7 \times 10^{52}} \sim 1.3 \times 10^{26} \ [\mathrm{cm}] \sim 40 \ [\mathrm{Mpc}] \tag{32}\]

のようになります。実際の銀河団からの熱制動放射由来のX線光子は、1秒間に1個くるか来ないか程度とされています。光子が飛来した部分は明るい点として表現されることから、観測結果はポチポチと点描のようなものになります。

上図はチャンドラX線衛星で観測された、ペルセウス座銀河団の中心部の様子です。上パネルは1.5-3.5keV、下パネルは3.5-7keVでの観測結果を示しています。ペルセウス座銀河団は73.6Mpcの距離にあります。先程の見積もりから、この銀河団からの熱制動放射光子は1秒間に1個も到達しません。 Fabian et al., 2003では、露出時間を95ks(およそ10万秒=28時間程度)としています。そのような長時間観測を行なって、ようやく先程のような銀河団のX線写真が撮れるのです。

X線で観測される熱制動放射の例

他にも、光学的に薄い高温プラズマから放出される熱制動放射由来の連続波成分は、以下のような天体から観測されています。

特にO, B型などの高温度星(早期型星とも呼ばれる)に分類されている、単一星のコロナやフレア
G, K, M型などの低温度星(晩期型星)の連星系のうち、特にactive binaryと呼ばれるフレア活動などを活発にしている連星系。これらは激しい時期活動によって、プラズマの加熱が行われている
主系列星から白色矮星に質量降着が起こっている連星系で、これらは特に激変星と呼ばれる。白色矮星に物質が降着する際に衝撃波が発生し、ガスの加熱が生じる
超新星残骸の衝撃波面では、星間物質が高温に加熱されている
楕円銀河や銀河群・銀河団に付随するプラズマ。ダークマターの重力ポテンシャルにより、高温プラズマが束縛されている

先程まで議論していた熱制動放射の値は、銀河団の典型的な値をもとに導出されたものです。もし他の系に対して考える場合には、規格化の値を変える必要があります。

参考文献

[1] 観山, 野本, 二間瀬, “天体物理学の基礎II”
[2] Fabian et al., 2003, “A deep Chandra observation of the Perseus cluster: shocks and ripples”
[3] 海老沢, 2014年度新潟大学理学部物理学科”プラズマ物理学特論”講義ノート
[4] 鶴, “宇宙物理入門”講義資料, 第8章: 熱制動輻射と銀河・銀河団の高温プラズマ