交換型不安定性 (interchange instability)

パーカー不安定性は磁力線がたわむような形状に変化するゆらぎが与えられたときに起こる不安定性でした。こちらの交換型不安定性は磁力線は変形せず、下図のようにその位置だけを上下に変化させます。

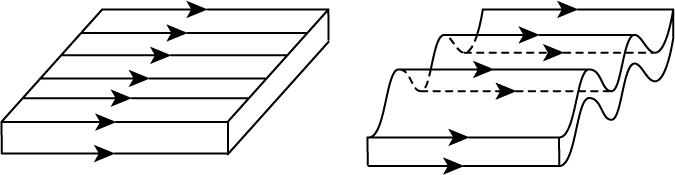
ここでは、この交換型不安定性の成長条件を求めてみましょう。

問題設定と基礎方程式の変形

鉛直下向きの一様重力$g$のもとで、成層を成している磁気流体を考えます。ガス密度$\rho$、磁場強度$B$、ガス圧$P$を持つ体積$V = S \ell$の流体円柱に摂動を加え、円柱が鉛直上向きに$dz$上昇する過程を考察しましょう。上に持ち上げたことにより円柱内のガス密度・磁場・ガス圧、そして円柱の体積はそれぞれ$\rho + \delta \rho, B + \delta B, P + \delta P, V' = S' \ell$に変化したとします。上昇した位置での円柱の外側での物理量はそれぞれ$\rho + d\rho, B + dB, P + dP$とします。さらに円柱が上向きに移動したとき、その側面から流体の流出入による混合は起こらないとします。

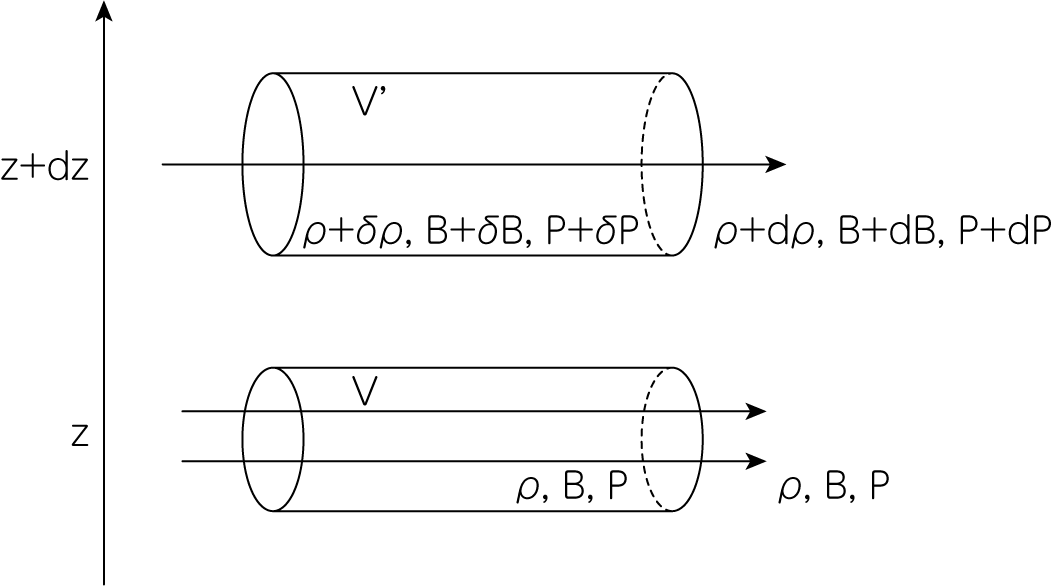
質量保存則より

\[\rho V = (\rho + \delta \rho) V' \tag{1}\]

また磁束保存より

\[BV = (B+ \delta B) V' \tag{2}\]

摂動を加えられた円柱は上昇しますが、このときの上昇は圧力平衡を保ちながら行われると仮定すると

\[P + \delta P + \frac{1}{8\pi} (B + \delta B)^2 = P + dP + \frac{1}{8\pi} (B + d B)^2 \tag{3}\]

断熱的に持ち上げることを考えて、ガスの圧力と密度の間には

\[P = K \rho^\gamma \tag{4}\]

が成り立っているとします。

式変形

以下の式変形では摂動量は十分小さく、例えば$\delta \rho, d\rho \ll \rho$などが成り立っているとします。ここから、摂動量の2次以上はさらに小さいため、無視する近似をおこないます。

(1), (2)式より

\[\frac{B}{\rho} = \frac{B + \delta B}{\rho + \delta \rho} = \frac{B}{\rho} \frac{1 + \frac{\delta B}{B}}{1 + \frac{\delta \rho}{\rho}} \simeq \frac{B}{\rho} \left( 1 + \frac{\delta B}{B} - \frac{\delta \rho}{\rho}\right) \ \Longrightarrow \ \frac{\delta B}{B} = \frac{\delta \rho}{\rho} \tag{5}\]

(3)式より

\[\delta P + \frac{1}{8\pi} (B^2 + 2 B \delta B) = dP + \frac{1}{8\pi} (B^2 + 2 B dB) \ \Longrightarrow \ \delta P + \frac{1}{4\pi} B \delta B = d P + \frac{1}{4\pi} B d B \tag{6}\]

(4)式より

\[P + \delta P = K (\rho + \delta \rho)^\gamma = K \rho^\gamma \left( 1 + \frac{\delta \rho}{\rho}\right)^\gamma \simeq \underbrace{K \rho^\gamma}_{(4)} \left( 1 + \gamma \frac{\delta \rho}{\rho}\right) = P + \gamma \frac{\delta \rho}{\rho} P \ \Longrightarrow \ \frac{\delta P}{P} = \gamma \frac{\delta \rho}{\rho} \tag{7}\]

(6)式に(5), (7)式を代入すると

\[\gamma \frac{P}{\rho} \delta \rho + \frac{B^2}{4\pi \rho} = dP + \frac{B}{4\pi} dB \ \Longrightarrow \ \delta \rho = \frac{dP + \frac{B}{4\pi} dB}{\frac{\gamma P}{\rho} + \frac{B^2}{4\pi \rho}} \tag{8}\]

ここまでの問題設定では圧力平衡になるまで上昇を続ける場合を考えてきました。しかし、もし$\delta \rho < d \rho$ならば、この流体円柱は浮力により上昇を続けます。この議論から

\[\frac{dP + \frac{B}{4\pi} dB}{\frac{\gamma P}{\rho} + \frac{B^2}{4\pi \rho}} < d\rho\]

が不安定性条件となります。これをさらに整理しましょう。両辺を$dz$で割ると

\[\frac{dP}{dz} + \frac{B}{4\pi} \frac{dB}{dz} < \left( \frac{\gamma P}{\rho} + \frac{B^2}{4\pi \rho} \right) \frac{d\rho}{dz}\]

この両辺において$\frac{1}{P} \frac{dP}{dz} = \frac{d \ln P}{dz}$のような変形を行うと

\[P \left(\frac{d\ln P}{dz} - \gamma \frac{d \ln \rho}{dz} \right) < \frac{B^2}{4\pi} \left( \frac{d \ln \rho}{dz} - \frac{d \ln B}{dz} \right) \ \Longrightarrow \ P \frac{d \ln \frac{P}{\rho^\gamma}}{dz} < - \frac{B^2}{4\pi} \frac{d \ln \frac{B}{\rho}}{dz}\]

ここで両辺を$\rho$で割り、さらにブルント-バイサラ振動数

\[N^2 = \frac{g}{\gamma} \frac{d}{dz} \ln \frac{P}{\rho^\gamma}\]

を用いると

\[\frac{1}{g} \frac{\gamma P}{\rho^\gamma} N^2 < - \frac{B^2}{4\pi \rho} \frac{d}{dz} \ln \frac{B}{\rho}\]

となります。最後に音速$C_s^2 = \gamma P / \rho$、そしてアルヴェーン波$v_A^2 = B^2 / 4\pi \rho$を用いれば

\[v_A^2 \frac{d}{dz} \ln \frac{B}{\rho} < - \frac{N^2}{g} C_s^2 \tag{9}\]

これが交換型不安定性の発生条件です。磁場がない、すなわち$B=0$のとき、$N^2<0$なら不安定であることがわかります。これは内部重力波で議論した対流不安定性に一致します。しかし$B \neq 0$の場合には、$\frac{B}{\rho}$が$z$に対して急激に減少すれば不安定となることを意味しています。

交換型不安定性の起こる例

中性子星磁気圏

中性子星が双極子磁場を持っている場合、その磁場の大きさは$B \propto r^{-3}$で減少します。そしてその中性子星磁気圏の周囲が降着円盤などの濃いガスで囲まれており降着が起こっているとすると、磁場とガス密度は大雑把には下図のような$r$依存性があると考えられます。中性子星の重力と自転運動により生まれる有効重力$g_\mathrm{eff}$も$r$に平行であれば、(9)の不安定性条件が成立し、交換型不安定性が発生します。

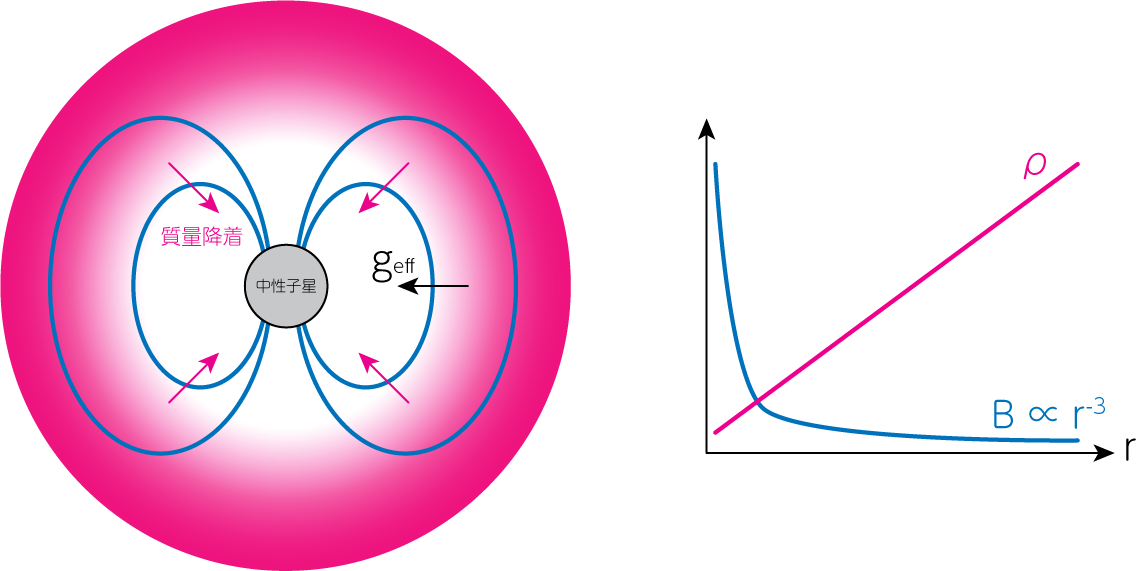
次の図は、中性子星磁気圏と降着円盤の相互作用をシミュレーションした計算例です。

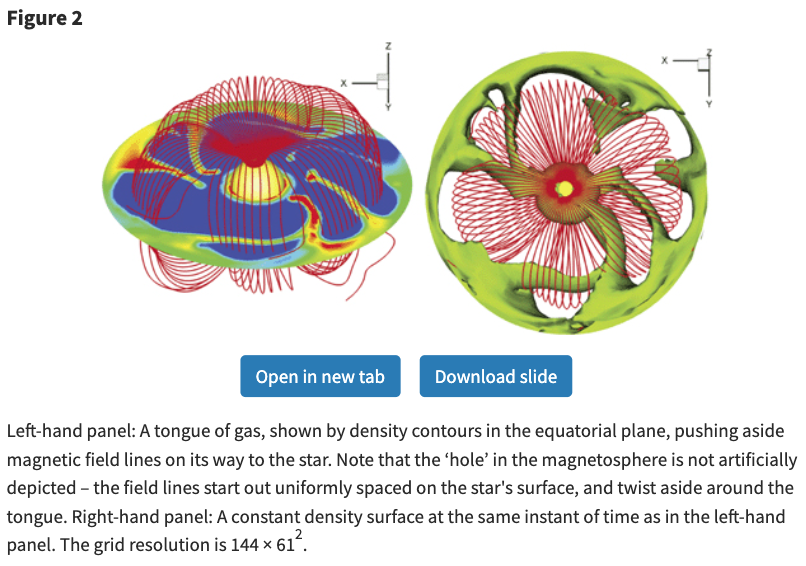
惑星磁気圏

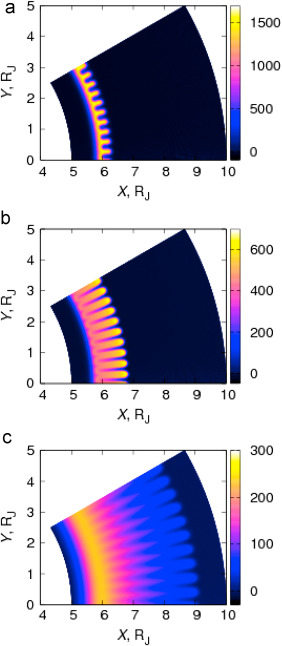
双極子磁場を持っていれば、先程の中性子星磁気圏と同じようなことが起こることが考えられます。下図は惑星磁気圏、特に木星の衛星イオのトーラスにおいて発生する交換型不安定性の計算例です。

参考文献

[1] 柴田一成, 福江純, 松元亮治, 嶺重慎, “活動する宇宙 -天体活動現象の物理-“
[2] Kulkarni & Romanova, 2008, “Accretion to magnetized stars through the Rayleigh-Taylor instability: global 3D simulations”
[3] Hiraki et al., 2012, “Io torus plasma transport under interchange instability and flow shears”