Table of contents
測地線偏差の方程式とその応用
ここでは隣接する2本の測地線について考え、その相対間隔の変化を記述する方程式を導出します。 なぜこのようなことを考えるかというと、そもそも、相対論において重要な概念である等価原理によれば、空間の1点に着目しているだけでは、重力の存在を知ることができないためです。 有限の距離だけ離れた2点間の相対運動を知ることで、その空間がどのような特徴を持っているのかを知ることができます。 そしてそれを求めるだけでなく、その方程式の応用についても見ていきましょう。
測地線偏差の方程式の導出
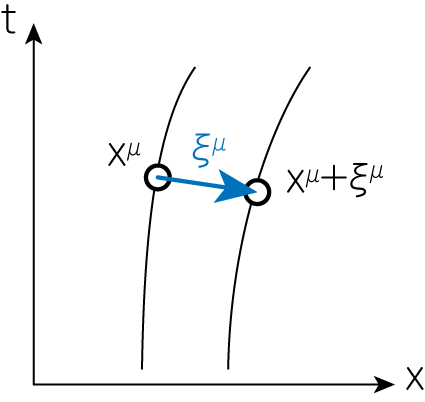
近接した2点\(x^\mu\)と\(x^\mu + \xi^\mu (\vert \xi^\mu \vert \ll x^\mu)\)にある2つの質点が満たす測地線方程式は、それぞれ以下で与えられます。
\[\frac{d^2 x^\mu}{d\tau^2} + \Gamma^\mu_{\ \ \alpha \beta} (x) \frac{dx^\alpha}{d\tau} \frac{dx^\beta}{d\tau} = 0 \tag{1}\] \[\frac{d^2 }{d\tau^2} (x^\mu + \xi^\mu) + \Gamma^\mu_{\ \ \alpha \beta} (x+\xi) \frac{d}{d\tau} (x^\alpha + \xi^\alpha) \frac{d}{d\tau} (x^\beta + \xi^\beta) = 0 \tag{2}\](2)式を\(\xi^\mu\)の1次までで展開しましょう。
\[\Gamma^\mu_{\ \ \alpha \beta} (x + \xi) \approx \Gamma^\mu_{\ \ \alpha \beta} (x) + \Gamma^\mu_{\ \ \alpha \beta, \gamma} \xi^\gamma \tag{3}\]ここで\(\Gamma^\mu_{\ \ \alpha \beta, \gamma} = \frac{d \Gamma^\mu_{\ \ \alpha \beta}}{dx^\gamma}\)です。 これより、(2)式は
\[\frac{d^2 x^\mu}{d\tau^2} + \frac{d^2 \xi^\mu}{d\tau^2} + (\Gamma^\mu_{\ \ \alpha \beta} + \Gamma^\mu_{\ \ \alpha \beta, \gamma} \xi^\gamma) \left( \frac{dx^\alpha}{d\tau} + \frac{d \xi^\alpha}{d\tau}\right) \left( \frac{dx^\beta}{d\tau} + \frac{d \xi^\beta}{d\tau}\right) = 0 \tag{4}\]のようになります。 (4)-(1)式を計算すると
\[\frac{d^2 \xi^\mu}{d\tau^2} + \Gamma^\mu_{\ \ \alpha \beta, \gamma} \xi^\gamma \frac{dx^\alpha}{d\tau} \frac{dx^\beta}{d\tau} + \Gamma^\mu_{\ \ \alpha \beta} \frac{d\xi^\alpha}{d\tau} \frac{dx^\beta}{d\tau} + \Gamma^\mu_{\ \ \alpha \beta} \frac{dx^\alpha}{d\tau} \frac{d\xi^\beta}{d\tau} = 0\]のようになり、さらに\(\Gamma^\mu_{\ \ \alpha \beta} = \Gamma^\mu_{\ \ \beta \alpha}\)というクリストッフェル記号の性質から
\[\frac{d^2 \xi^\mu}{d\tau^2} + \Gamma^\mu_{\ \ \alpha \beta, \gamma} \xi^\gamma \frac{dx^\alpha}{d\tau} \frac{dx^\beta}{d\tau} + 2 \Gamma^\mu_{\ \ \alpha \beta} \frac{d\xi^\alpha}{d\tau} \frac{dx^\beta}{d\tau} = 0 \tag{5}\]を得ます。 式の見通しを良くするために、微分を絶対微分(測地線に沿った方向の微分)を用いて書き直していきましょう。 絶対微分は以下のように書かれます。
\[\frac{D \xi^\mu}{D \tau} \equiv \frac{d\xi^\mu}{d\tau} + \Gamma^\mu_{\ \ \alpha \beta} \xi^\alpha \frac{d x^\beta}{d\tau} \tag{6}\]これを用いて\(\frac{D^2 \xi^\mu}{D\tau^2}\)を計算します。
\[\begin{align} \frac{D^2 \xi^\mu}{D\tau^2} &= \frac{d}{d\tau} \left( \frac{D\xi^\mu}{D\tau}\right) + \Gamma^\mu_{\ \ \alpha \beta} \frac{D\xi^\alpha}{D\tau} \frac{d x^\beta}{d\tau} = \frac{d}{d\tau} \left( \frac{d \xi^\mu}{d\tau} + \Gamma^\mu_{ \ \ \alpha \beta} \xi^\alpha \frac{dx^\beta}{d\tau} \right) + \Gamma^\mu_{\ \ \alpha \beta} \left( \frac{d\xi^\alpha}{d\tau} + \Gamma^\alpha_{\ \ \gamma \delta} \xi^\gamma \frac{dx^\delta}{d\tau} \right) \frac{dx^\beta}{d\tau} \notag \\ &= \frac{d^2 \xi^\mu}{d\tau^2} + \frac{d\Gamma^\mu_{\ \ \alpha \beta}}{d\tau} \xi^\alpha \frac{dx^\beta}{d\tau} + \Gamma^\mu_{\ \ \alpha \beta} \left( \frac{d\xi^\alpha}{d\tau} \frac{dx^\beta}{d\tau} + \xi^\alpha \frac{d^2 x^\beta}{d\tau^2}\right) + \Gamma^\mu_{\ \ \alpha \beta} \frac{d\xi^\alpha}{d\tau} \frac{dx^\beta}{d\tau} + \Gamma^\mu_{\ \ \alpha \beta} \Gamma^\alpha_{\ \ \gamma \delta} \xi^\gamma \frac{dx^\delta}{d\tau} \frac{dx^\beta}{d\tau} \tag{7} \end{align}\]ここで
\[\frac{d}{d\tau} = \frac{dx^\gamma}{d\tau} \frac{d}{dx^\gamma}\]を用いると、\(\Gamma\)の微分を持つ第二項は
\[(第二項) = \frac{dx^\gamma}{d\tau} \Gamma^\mu_{\ \ \alpha \beta, \gamma} \xi^\alpha \frac{dx^\beta}{d\tau} \tag{8}\]のように計算されます。 さらに測地線方程式(1)より
\[\frac{D^2 \xi^\mu}{D\tau^2} = \frac{d^2 \xi^\mu}{d\tau^2} + \Gamma^\mu_{\ \ \alpha \beta, \gamma} \xi^\alpha \frac{dx^\beta}{d\tau} \frac{dx^\gamma}{d\tau} + 2 \Gamma^\mu_{\ \ \alpha \beta} \frac{d\xi^\alpha}{d\tau} \frac{dx^\beta}{d\tau} - \Gamma^\mu_{\ \ \alpha \beta} \Gamma^\beta_{\ \ \gamma \delta} \xi^\alpha \frac{dx^\gamma}{d\tau} \frac{dx^\delta}{d\tau} + \Gamma^\mu_{\ \ \alpha \beta} \Gamma^\alpha_{\ \ \gamma \delta} \xi^\gamma \frac{dx^\delta}{d\tau} \frac{dx^\beta}{d\tau} \tag{9}\]のようになります。 (5), (9)式より
\[\frac{D^2 \xi^\mu}{D\tau^2} = - \Gamma^\mu_{\ \ \alpha \beta, \gamma} \xi^\gamma \frac{dx^\alpha}{d\tau} \frac{dx^\beta}{d\tau} + \Gamma^\mu_{\ \ \alpha \beta, \gamma} \xi^\alpha \frac{dx^\beta}{d\tau} \frac{dx^\gamma}{d\tau} - \Gamma^\mu_{\ \ \alpha \beta} \Gamma^\beta_{\ \ \gamma \delta} \xi^\alpha \frac{dx^\gamma}{d\tau} \frac{dx^\delta}{d\tau} + \Gamma^\mu_{\ \ \alpha \beta} \Gamma^\alpha_{\ \ \gamma \delta} \xi^\gamma \frac{dx^\delta}{d\tau} \frac{dx^\beta}{d\tau}\]となります。 さらに添字のダミー変数を操作することにより、\(\frac{dx^\alpha}{d\tau} \xi^\beta \frac{dx^\gamma}{d\tau}\)でまとめることで
\[\frac{D^2 \xi^\mu}{D\tau^2} - (\Gamma^\mu_{\ \ \alpha \gamma, \beta} - \Gamma^\mu_{\ \ \alpha \beta, \gamma} + \Gamma^\mu_{\ \ \delta \beta} \Gamma^\delta_{\ \ \alpha \gamma} - \Gamma^\mu_{\ \ \delta \gamma} \Gamma^\delta_{\ \ \alpha \beta}) \frac{dx^\alpha}{d\tau} \xi^\beta \frac{dx^\gamma}{d\tau} = 0 \tag{10}\]を得ます。 ここで、左辺の\((\cdots)\)の部分とリーマンテンソルを見比べることで
\[\frac{D^2 \xi^\mu}{D \tau^2} + R^\mu_{\ \ \alpha \beta \gamma} \frac{dx^\alpha}{d\tau} \xi^\beta \frac{dx^\gamma}{d\tau} = 0 \tag{11}\]のようになることがわかります。 これが測地線偏差の方程式です。 これは2本の測地線が相対的な距離\(\xi\)だけ離れて存在していたとき、その\(\xi\)の二階微分、すなわち相対的な加速度が空間の曲がり具合を表現する\(R^\mu_{\ \ \alpha \beta \gamma}\)に依存することを表しています。 たとえばミンコフスキー時空のような平坦な空間では\(R^\mu_{\ \ \alpha \beta \gamma} = 0\)となり、2本の測地線の相対的な距離は一定のままです。 しかし重力などにより空間に歪みが生じると、2本の測地線の相対距離が伸びたり縮んだりすることがわかります。
応用: 重力波の検出原理とレーザー干渉計
変位の大きさの見積もり
測地線偏差の方程式を用いて、重力波の検出原理について学びましょう。 地球上で重力波を観測することを考えると、その観測者は非相対論的な運動はしていないと考えてよく
\[d\tau \approx dt, \quad \frac{dx^0}{d\tau} \approx c, \quad \frac{dx^i}{d\tau} \approx 0 \tag{12}\]と近似できます。 すると(11)式は
\[\frac{d\xi^\mu}{dt^2} = c^2 R^\mu_{\ \ 0 \beta 0} \xi^\beta\]となります。 さらにリーマンテンソルに対しては
\[R^\mu_{\ \ 0 0 0} = \Gamma^\mu_{\ \ 00, 0} - \Gamma^\mu_{\ \ 00, 0} + \Gamma^\mu_{\ \ \delta 0} \Gamma^\delta_{\ \ 00} - \Gamma^\mu_{\ \ \delta 0} \Gamma^\delta_{\ \ 00} = 0\]が常に成り立つため
\[\frac{d^2\xi^i}{dt^2} + c^2 R^i_{\ \ 0 j 0} \xi^j = 0 \tag{12}\]と書くことができます。 ここで、地上での空間座標の変化を見るために、以降では空間成分\(i\)だけを考えていきます。 \(g_{\mu \nu} = \eta_{\mu \nu} + h_{\mu \nu}\)のように計量を書いたとき、TTゲージにさらにローレンツ条件を課すことで
\[(h_{\mu \nu} ) = \left( \begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & h_+ & h_\times & 0 \\ 0 & h_\times & -h_+ & 0 \\ 0 & 0 & 0 & 0 \end{array} \right) \tag{13}\]のようになるのでした。 ここから(12)式のリーマンテンソル成分を計算しましょう。
\[R^i_{\ \ 0j0} = \Gamma^i_{\ \ 00,j} - \Gamma^i_{\ \ 0j,0} + \mathcal{O}(h^2) \tag{14}\]さらに、クリストッフェル記号は
\[\Gamma^i_{\ \ 00} = \frac{1}{2} g^{\nu i} (g_{0\nu, 0} + g_{\nu 0, 0} - g_{00, \nu}) = g^{\ \ \ i}_{0 \ \ , 0} - \frac{1}{2} g^{\ \ \ \ , i}_{00} \approx 0 \tag{15}\] \[\Gamma^i_{\ \ 0j} = \frac{1}{2} g^{\nu i} (g_{j\nu, 0} + g_{\nu 0, j} - g_{0j, \nu}) = \frac{1}{2} (g^{\ \ \ i}_{j \ \ \ , 0} + g^i_{\ \ 0, j} - g_{0j}^{\ \ \ \ , i}) \approx \frac{1}{2} h^{\ \ \ i}_{j \ \ \, 0} = \frac{1}{2c} \frac{\partial h^{\ \ \ i}_j}{\partial t} \tag{16}\]のように計算されます。 以上より
\[\frac{d^2 \xi^i}{dt^2} = \frac{1}{2} \frac{\partial^2 h^{\ \ \ i}_j}{\partial t^2} \xi^j \tag{17}\]となります。
初期に\(\xi_0^i\)の距離にあった2点が、重力波が通過したことで
のように変化したとしましょう。 (17)式を用いて、\(h^{\ \ \ i}_j \simeq h e^{-i\omega t}\)の重力波が入射したときの位置の変化を大雑把に見積もってみます。
\[(17) \ \Longrightarrow \ \frac{\Delta \xi}{\Delta t^2} \approx \frac{h e^{-i \omega t}}{2 \Delta t^2} (\xi_0 + \Delta \xi) \underbrace{\approx}_{\xi_0 \gg \Delta \xi} \frac{h \xi_0 e^{-i \omega t}}{2 \Delta t^2} \ \Longrightarrow \ \Delta \xi \approx h \xi_0 e^{-i \omega t} \tag{19}\]ここから、振幅の大きさは
\[\vert \Delta \xi \vert \approx 10^{-14} \left( \frac{h}{10^{-21}}\right) \left( \frac{\xi_0}{100 \mathrm{km}}\right) \quad [\mathrm{cm}] \tag{20}\]のように、非常に小さいことがわかります。 参考までに、原子核の大きさはおよそ\(1\mathrm{fm} (=10^{-13})\mathrm{cm}\)程度です。 様々なノイズがある中で、原子核程度の振動を検出する必要があることから、重力波検出の難しさが伺えます。 また(20)式からわかるように、2点の長さ\(\xi_0\)が長いほど、より微弱な重力波信号を検出できるようになるとわかります。 ここから、重力波検出器を宇宙空間に飛ばし、レーザー干渉計を用いて重力波を検出しようとする試みが考えられています。
レーザー干渉計を用いた重力波検出器
すでに用語が出てきていますが、このとても小さな変位をマイケルソン型のレーザー干渉計で検出します。 実際には小さな変位で生じた位相差を、レーザーで観測するのです。 下図のように\(x\)軸と\(y\)軸の方向に腕を持つようなマイケルソン干渉計に、\(z\)方向から\(+\)モードの重力波が入射してきたとします。 また、中央にあるビームスプリッターから\(x, y\)軸上にある鏡までの距離をそれぞれ\(\xi_x, \xi_y\)とし、レーザー光の角周波数を\(\omega\)とします。
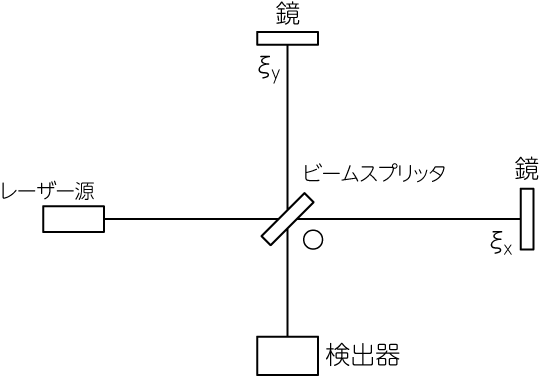
このときの微小線素は
\[ds^2 = -c^2 dt^2 + (1+h_+(t)) dx^2 + (1-h_+(t)) dy^2 + dz^2 \tag{21}\]のように書かれます。
まずは\(x\)軸方向に往復するレーザー光について考えましょう。 この場合、\(dy = dz = 0\)と考えられるため
のようになります。 ここから
\[dx = \pm \frac{c dt}{\sqrt{1+h_+}} \approx \pm \left( 1-\frac{h_+}{2}\right) cdt \tag{23}\]を得ます。 途中、\(\vert h_+ \vert \ll 1\)として、近似を行いました。 光子がビームスプリッターと鏡の間を往復するのにかかる時間を\(\Delta t_x\)としましょう。 この時間間隔で両辺を積分すると
\[c \int_t^{t+\Delta t_x} \left( 1-\frac{1}{2} h_+\right) dt = c \Delta t_x - \frac{c}{2} \int_t^{t+ \Delta t_x} h_+ dt = 2 \xi_x\]となります。 ここでプラス・マイナスの符号は、\(\xi^x > 0\)からプラスを選択しました。 以上から
\[\Delta t_x = \frac{2\xi_x}{c} + \frac{1}{2} \int_t^{t+ \Delta t_x} h_+ dt \tag{24}\]のように計算されます。 重力波の入射がない場合(\(h_+ = 0\))、\(\Delta t_x = \frac{2 \xi_x}{c}\)となります。 ここから第二項が重力波による影響を表していることがわかります。 しかしこの項は第一項に比べて十分小さいとすると、(24)式の積分範囲の上限の部分は
\[\Delta t_x \approx \frac{2\xi_x}{c} + \frac{1}{2} \int_t^{t+ \frac{2\xi_x}{c}} h_+ dt \tag{25}\]のように近似して差し支えないでしょう。 よって、レーザー光が\(x\)軸を往復する間に受ける位相変化を\(2 \phi_x\)と書くと
\[2\phi_x = \omega \Delta t_x \approx \frac{2\xi^x \omega}{c} + \frac{\omega}{2} \int_t^{t+ \frac{2\xi_x}{c}} h_+ dt \tag{26}\]と求まります。 同様に、レーザー光が\(y\)軸を往復する間に受ける位相変化\(2\phi_y\)は
\[2\phi_y \approx \frac{2\xi^y \omega}{c} - \frac{\omega}{2} \int_t^{t+ \frac{2\xi_y}{c}} h_+ dt \tag{27}\]となります。 \(x, y\)方向のそれぞれのアームの長さを\(\xi_x \simeq \xi_y \simeq \ell\) (ただし\(\ell_- \equiv \xi_x - \xi_y > 0\))とすると、両方のアームでレーザー光が受ける位相変化の差\(2\phi_-\)は
\[\begin{align} 2\phi_- (t) &= 2\phi_x - 2\phi_y = \frac{2\ell_- \omega}{c} + \frac{\omega}{2} \left(\int_t^{t+ \frac{2\xi_x}{c}} h_+ dt + \int_t^{t+ \frac{2\xi_y}{c}} h_+ dt\right) \notag \\ &\underbrace{\approx}_{\xi_x, \xi_y \simeq \ell} \frac{2\ell_- \omega}{c} + \omega \int_t^{t+ \frac{2\ell}{c}} h_+ dt \tag{28} \end{align}\]のように変形されます。 第一項は元々の2本のアームの距離が違うことから生じる位相差、そして第二項が重力波の通過に伴ってアームの距離が伸び縮みすることから生まれる位相差です。
参考文献
[1] 須藤靖, “もうひとつの一般相対論入門”
[2] 川村静児, “重力波物理の最前線”
[3] 和泉究, JAXAウェブサイト, “重力波観測のこれまで、これから”