Table of contents
力学平衡な磁気流体回転トーラス
コンピュータの性能が大幅に向上し、近年では降着円盤の磁気流体計算が活発に行われるようになりました。また最近ではM87に引き続き、私たちがいる天の川銀河の中心に存在するSMBH(Super Massive Black Hole; 超巨大質量ブラックホール)が直接撮像された観測結果が登場するなど、この分野が盛り上がりを見せています。ここでは降着円盤シミュレーションの初期条件として用いられる、磁気流体回転トーラスの式を導出します。
\(\varphi\)方向磁場を持つ場合
ここでは円形磁場が貫いている回転トーラスを考えましょう。なお、外場として与えられている重力ポテンシャルは軸対称で、\(\Phi (R, z)\)で与えられるとします。このトーラスは力学平衡にあると考えて
\[(遠心力) = (ポテンシャルの勾配による力) + (圧力勾配による力) + (磁気張力)\]が成り立っているとします。また、トーラスを構成しているガスの単位質量あたりの角運動量\(L_z\)が
\[L_z = R v_\varphi = \ell_z \left( \frac{R}{R_b}\right)^a \tag{1}\]のように、回転軸からの距離\(R\)に依存する形を考えます。ここで\(R_b\)はトーラスにおいて一番密度が大きくなる(トーラスの最深部の)座標であり、\(L_z(R_b) = \ell_z\)はトーラス最深部の単位体積あたりの角運動量です。
釣り合いの式
まずは\(R\)方向の釣り合いの式からです。円形磁場を仮定しているため、磁気張力は簡単な形となることを利用して
\[\frac{L_z^2}{R^3} = \frac{\partial \Phi}{\partial R} + \frac{1}{\rho} \frac{\partial}{\partial R} (P_\mathrm{gas} + P_\mathrm{mag}) + \frac{1}{4\pi \rho} \frac{B_\varphi^2}{R} = \frac{\partial \Phi}{\partial R} + \frac{1}{\rho} \frac{\partial P_\mathrm{gas}}{\partial R} + \frac{1}{8\pi \rho} \frac{\partial B_\varphi^2}{\partial R} + \frac{1}{4\pi \rho} \frac{B_\varphi^2}{R}\]式変形のために
\[B_\varphi \frac{\partial}{\partial R} (R B_\varphi) = B_\varphi^2 + R B_\varphi \frac{\partial B_\varphi}{\partial R} = B_\varphi^2 + \frac{1}{2} R \frac{\partial B_\varphi^2}{\partial R} \ \Longrightarrow \ \frac{B_\varphi}{R} \frac{\partial}{\partial R} (R B_\varphi) = \frac{B_\varphi^2}{R} + \frac{1}{2} \frac{\partial B_\varphi^2}{\partial R}\]と(1)式を用いると
\[\frac{\ell_z^2}{R_b^{2a}} R^{2a-3} = \frac{\partial \Phi}{\partial R} + \frac{1}{\rho} \frac{\partial P_\mathrm{gas}}{\partial R} + \frac{1}{4\pi \rho} \frac{B_\varphi}{R} \frac{\partial}{\partial R} (R B_\varphi) \tag{2}\]続いて\(z\)成分です。\(z\)方向には磁気張力は働かないため
\[0 = \frac{\partial \Phi}{\partial z} + \frac{1}{\rho} \frac{\partial}{\partial z} (P_\mathrm{gas} + P_\mathrm{mag}) \ \Longrightarrow \ \frac{\partial \Phi}{\partial z} + \frac{1}{\rho} \frac{\partial P_\mathrm{gas}}{\partial z} + \frac{B_\varphi}{4\pi \rho} \frac{\partial B_\varphi}{\partial z} = 0 \tag{3}\]トーラスの構造
ここで、初期のトーラスの構造はポリトロープを仮定します。すなわち
\[P_\mathrm{gas} = K \rho^\Gamma \tag{4}\]の形であるとします。ここで\(K, \Gamma\)は定数です。
ポリトロープは構造を仮定するとき用いることもあれば、局所的な状態方程式を仮定するときにも用いる、今だに理解できていない式です...
さらに円形磁場によるアルヴェーン速度を
\[v_{A\varphi}^2 = \frac{B_\varphi^2}{4\pi \rho} = \frac{(4\pi H)^{1/\mu}}{4\pi} (R B_\varphi)^{\frac{2(\mu-1)}{\mu}} \tag{5}\]のように仮定します。ここで\(H, \mu\)も定数です。するとこの仮定から
\[\frac{4\pi v_{A\varphi}^2}{(4\pi H)^{1/\mu}} = (R B_\varphi)^{\frac{2(\mu-1)}{\mu}} \ \Longrightarrow \ B_\varphi = \frac{1}{R} \left\{ \frac{4\pi v_{A\varphi}^2}{(4\pi H)^{1/\mu}}\right\}^{\frac{\mu}{2(\mu-1)}} \tag{6}\](2), (4)式より
\[\frac{\ell_z^2}{R_b^{2a}} R^{2a-3} = \frac{\partial \Phi}{\partial R} + \frac{1}{\rho} \frac{\partial}{\partial R} (K \rho^\Gamma) + \frac{1}{4\pi \rho} \frac{B_\varphi}{R} \frac{\partial}{\partial R} (R B_\varphi)\]さらに(6)式から
\[\begin{aligned} &\frac{\partial v_{A\varphi}^2}{\partial R} = \frac{(4\pi H)^{1/\mu}}{4\pi} \frac{\partial}{\partial R} (R B_\varphi)^{\frac{2(\mu-1)}{\mu}} = \frac{(4\pi H)^{1/\mu}}{4\pi} \frac{2(\mu-1)}{\mu} (R B_\varphi)^{\frac{2(\mu-1)}{\mu}-1} \frac{\partial}{\partial R} (R B_\varphi) = \frac{2(\mu-1)}{\mu} \frac{v_{A\varphi}^2}{R B_\varphi} \frac{\partial}{\partial R} (R B_\varphi) \\ &\Longrightarrow \ \frac{\partial}{\partial R} (R B_\varphi) = \frac{\mu}{2(\mu-1)} \frac{R B_\varphi}{v_{A\varphi}^2} \frac{\partial v_{A\varphi}^2}{\partial R} \end{aligned}\]より
\[\frac{\ell_z^2}{R_b^{2a}} R^{2a-3} = \frac{\partial \Phi}{\partial R} + K \Gamma \rho^{\Gamma-2} \frac{\partial \rho}{\partial R} + \frac{\mu}{2(\mu-1)} \frac{\partial v_{A\varphi}^2}{\partial R} = \frac{\partial \Phi}{\partial R} + K \frac{\Gamma}{\Gamma-1} \frac{\partial \rho^{\Gamma-1}}{\partial R} + \frac{\mu}{2(\mu-1)} \frac{\partial v_{A\varphi}^2}{\partial R}\]のようになります。ここで(4)式から、ガスの音速は
\[C_s^2 = \frac{\partial P_\mathrm{gas}}{\partial \rho} = K \Gamma \rho^{\Gamma-1}\]となるので
\[-\frac{\ell_z^2}{R_b^{2a}} R^{2a-3} + \frac{\partial \Phi}{\partial R} + \frac{1}{\Gamma-1} \frac{\partial C_s^2}{\partial R} + \frac{\mu}{2(\mu-1)} \frac{\partial v_{A\varphi}^2}{\partial R} = 0\]の形になります。この両辺を\(R\)で積分すると
\[- \frac{1}{2a-2}\frac{\ell_z^2}{R_b^{2a}} R^{2a-2} + \Phi + \frac{C_s^2}{\Gamma-1} + \frac{\mu}{2(\mu-1)} v_{A\varphi}^2 = (Rに依存しない関数) \tag{7}\]を得ます。続けて\(z\)方向の釣り合いの式(3)も同様に式変形しましょう。全く同じ式変形により、以下を得ます。
\[\frac{\partial \Phi}{\partial z} + \frac{1}{\Gamma-1} \frac{\partial C_s^2}{\partial z} + \frac{\mu}{2(\mu-1)} \frac{\partial v_{A\varphi}^2}{\partial z} = 0\]この両辺を\(z\)で積分すると
\[\Phi + \frac{C_s^2}{\Gamma-1} + \frac{\mu}{2(\mu-1)} v_{A\varphi}^2 = (zに依存しない関数) \tag{8}\]を得ます。
トーラスの密度分布の解
(7), (8)式より
\[- \frac{1}{2a-2} \frac{\ell_z^2}{R_b^{2a}} R^{2a-2} + (zに依存しない関数) = (Rに依存しない関数)\]左辺は\(R\)のみの関数なのに対し、右辺は\(z\)のみの関数です。よってこれは定数のポテンシャルの形で書けることがわかります。ついでに\(\mu = \Gamma\)としてしまうと
\[-\frac{1}{2a-2} \frac{\ell_z^2}{R_b^{2a}} R^{2a-2} + \Phi + \frac{C_s^2}{\Gamma-1} + \frac{\Gamma}{2(\Gamma-1)} v_{A\varphi}^2 \equiv \Psi_b \tag{8}\]のように書けます。ここで\(\Psi_b\)は定数です。
(5)式より
です。これよりトーラス最深部でのアルヴェーン速度は
\[v_{A\varphi}^2 = H R^{2(\Gamma-1)} \rho^{\Gamma-1} \ \Longrightarrow \ v_{A\varphi, b}^2 = H R_b^{2(\Gamma-1)} \rho_b^{\Gamma-1} \tag{9}\]そしてトーラス最深部での音速から、定数\(K\)は
\[C_{s, b}^2 = \Gamma K \rho_b^{\Gamma-1} \ \Longrightarrow \ K = \frac{C_{s, b}^2}{\Gamma \rho_b^{\Gamma-1}} \tag{10}\]となります。さらに新しいパラメータとして、\(\varphi\)方向磁場によるトーラス最深部でのプラズマベータ\(\beta_{\varphi, b}\)を導入すると
\[\beta_{\varphi, b} = \frac{P_{\mathrm{gas}, b}}{P_{\mathrm{mag}, b}} = \frac{K \rho_b^\Gamma}{\frac{1}{8\pi} B_{\varphi, b}^2} = \frac{K\rho_b^\Gamma}{\frac{1}{2} \rho_b v_{A\varphi, b}^2} \underbrace{=}_{(9)} \frac{K \rho_b^\Gamma}{\frac{1}{2} H R_b^{2(\Gamma-1)} \rho_b^\Gamma} \ \Longrightarrow \ H = \frac{2K}{\beta_{\varphi, b}} R_b^{-2(\Gamma-1)} \tag{11}\]のように定数\(H\)が求まります。
(8)式において、\(\Psi_b\)をトーラス最深部\((R, z) = (R_b, z)\)でのポテンシャルの値とすると
ガス密度\(\rho(R, z)\)を求めるために式変形をしましょう。
\[\begin{aligned} \Psi_b - \Phi(R, z) + \frac{1}{2a-2} \frac{\ell_z^2}{R_b^{2a}} R^{2a-2} &= \frac{\overbrace{C_s^2}^{=\Gamma P_\mathrm{gas}/\rho}}{\Gamma-1} + \frac{\Gamma}{2(\Gamma-1)} \underbrace{v_{A\varphi}^2}_{(9)} = \frac{\Gamma}{\Gamma-1} \left( \frac{P_\mathrm{gas}}{\rho} + \frac{1}{2} H R^{2(\Gamma-1)} \rho^{\Gamma-1}\right) \\ &\underbrace{=}_{(4)} \frac{\Gamma}{\Gamma-1} K \rho^{\Gamma-1} \left( 1 + \frac{H}{2K} R^{2(\Gamma-1)}\right) \\ &= \frac{\Gamma}{\Gamma-1} K \rho^{\Gamma-1} \left( 1 + \frac{H}{2K} R_b^{2(\Gamma-1)} R_b^{-2(\Gamma-1)} R^{2(\Gamma-1)}\right) \end{aligned}\]ここに(11)式を用いれば
\[\Psi_b - \Phi + \frac{1}{2a-2} \frac{\ell_z^2}{R_b^{2a}} R^{2a-2} = \frac{\Gamma}{\Gamma-1} K \rho^{\Gamma-1} \left\{ 1 + \beta_{\varphi, b}^{-1} \left( \frac{R}{R_b} \right)^{2(\Gamma-1)} \right\}\]よって、求めたかった磁気流体回転トーラスの密度分布は
\[\rho (R, z) = \left[ \frac{\Psi_b - \Phi(R, z) + \frac{1}{2a-2} \frac{\ell_z^2}{R_b^{2a}} R^{2a-2}}{\frac{\Gamma}{\Gamma-1} K \left\{ 1 + \beta_{\varphi, b}^{-1} \left( \frac{R}{R_b} \right)^{2(\Gamma-1)} \right\}}\right]^{\frac{1}{\Gamma-1}}\]のようになります。実際には\([\cdots]\)の中身の分子が負になる領域が存在します。よって、このトーラスのガス分布は
\[\rho (R, z) = \left[ \frac{ \max \left( \Psi_b - \Phi(R, z) + \frac{1}{2a-2} \frac{\ell_z^2}{R_b^{2a}} R^{2a-2}, 0\right)}{\frac{\Gamma}{\Gamma-1} K \left\{ 1 + \beta_{\varphi, b}^{-1} \left( \frac{R}{R_b} \right)^{2(\Gamma-1)} \right\}}\right]^{\frac{1}{\Gamma-1}} \tag{12}\]のように書くのが正しいでしょう。
磁場の大きさ
\(B_\varphi\)は(9.0)式と(11)式より
\[B_\varphi^2 = \frac{8\pi K}{\beta_{\varphi, b}} \left( \frac{R}{R_b}\right)^{2(\Gamma-1)} \rho^\Gamma \tag{13}\]です。ここで\(K\)は、(10)式と理想気体の状態方程式
\[P_\mathrm{gas} = n k_B T = \frac{\rho}{\mu m_p} k_B T \ \Longrightarrow \ C_s^2 = \frac{\Gamma P_\mathrm{gas}}{\rho} = \frac{\Gamma}{\mu m_p} k_B T \tag{14}\]を用いれば
\[K = \frac{k_B }{\mu m_p} \frac{T}{\rho^{\Gamma-1}} = \frac{k_B }{\mu m_p} \frac{T_b}{\rho_b^{\Gamma-1}} \tag{15}\]のようになります。(15)式の最後の等号は、\(K\)が定数であることからトーラス最深部の値を用いて記述できることを用いました。
以上から
- トーラス最深部の位置\(R_b\)
- \(L_z\)の\(R\)依存性\(a\)
- トーラス最深部での単位体積あたりの角運動量\(\ell_z\)
- トーラス最深部でのプラズマベータ\(\beta_{\varphi, b}\)
- トーラス最深部でのガス密度\(\rho_b\)
- トーラス最深部での温度\(T_b\)
- ポリトロープ指数\(\Gamma=1+ \frac{1}{n}\)
をパラメータとして人間が入力すれば、トーラスの密度分布と\(\varphi\)方向磁場分布を計算することができます。
磁場なしトーラスの場合
磁場のないガストーラスを用意したい場合は、(12)式において\(\beta_{\varphi, b} \rightarrow \infty\)とすれば得られます。すると
\[\rho (R, z) = \left[ \frac{ \max \left( \Psi_b - \Phi(R, z) + \frac{1}{2a-2} \frac{\ell_z^2}{R_b^{2a}} R^{2a-2}, 0\right)}{\frac{\Gamma}{\Gamma-1} K}\right]^{\frac{1}{\Gamma-1}} \tag{16}\]となります。
ポロイダル磁場を持つトーラスの場合
ポロイダル(\(R, z\)成分しか持たない)磁場をトーラス内部に持つことを考える場合、一般に釣り合いの式を解くことは困難です。このため、よく用いられる磁場の用意手法としては、次のようなものがあります。
磁場のベクトルポテンシャルを\(\mathbf{A} = A_\varphi \mathbf{e}_\varphi\)のように定めると、このベクトルポテンシャルから発生する磁場は
のようにポロイダル磁場となります。よってベクトルポテンシャル\(A_\varphi\)を適当に、例えば\(A_\varphi \propto \rho\)のように定めます。あるいは
\[A_\varphi = A_0 \exp \left\{ - \left( \frac{R-R_b}{a} \right)^2 - \left(\frac{z}{b} \right)^2 \right\}\]のように、適当なscale height \(a, b\)を用いることで、トーラスの限られた領域内にポロイダル磁場が存在するようなモデルが作れます。ただし(16)式の磁場なしトーラスにポロイダル磁場を勝手に加えることで、力学平衡からズレが生じます。よってこのポロイダル磁場ありトーラスは、力学平衡が成り立っていないことに注意しましょう。
またこのようにして加えられたポロイダル磁場は、その向きに注意する必要があります。もしブラックホール降着円盤のような系のシミュレーション初期条件として用いる場合、このベクトルポテンシャル\(A_\varphi\)は降着円盤中を流れる電流によって作られると考えることができます。すると下図のように、その電流から右ねじの法則が成り立つように磁場の向き(ここではベクトルポテンシャルの符号)を定めなければなりません。
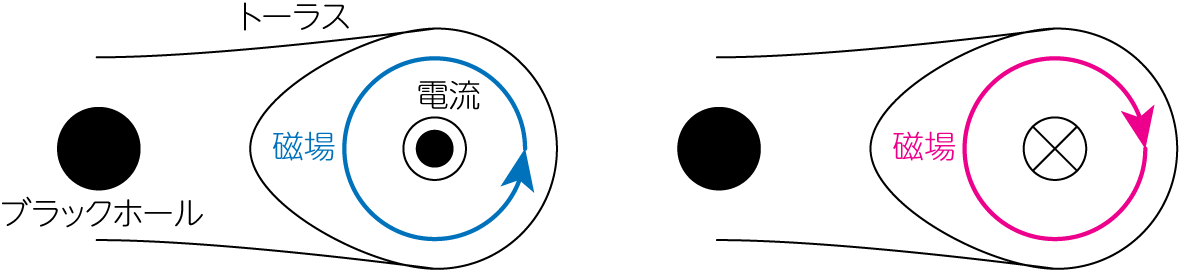
トーラスの周囲について
先述の通り、(12)式や(16)式で表されるようなトーラスでは、ガス密度が0になる領域が存在します。しかし(磁気)流体シミュレーションなどを行う場合、\(\rho = 0\)では音速\(C_s^2 = \frac{\gamma P_\mathrm{gas}}{\rho}\)やアルヴェーン速度\(v_A = \frac{B}{\sqrt{4\pi \rho}}\)が無限大となり、計算が不可能となります。
そこで降着円盤などのシミュレーションでは、トーラスの周囲に静水圧平衡な定温コロナ(ハロー)を配置します。\(R\)方向の釣り合いの式より
ここに理想気体の状態方程式(14)式を用います。このとき、このコロナ成分は温度が一定であることを用いると、上の釣り合いの式は\(R\)で積分することができて
\[C = - \Phi - \frac{k_B T}{\mu m_p} \ln \rho_c\]となります。左辺の\(C\)は積分定数です。以上から
\[\rho_c = \exp\left\{ \frac{\mu m_p}{k_B T} (-\Phi -C)\right\} = \rho_{c, 0} \exp \left\{ - \frac{\mu m_p}{k_B T} (\Phi - \Phi_b)\right\} \tag{17}\]となります。ここで\(\Phi_b = \Phi(R_b, 0)\)です。積分定数をこのように定めておけば、トーラスの最深部\((R_b, 0)\)でのコロナ成分のガス密度が\(\rho_{c, 0}\)であると一眼で判断することができて便利です。
コラム的な?: なぜ「平衡状態」にこだわるのか?
例えば、トーラス中で発生する不安定性(例えば弱磁場により起こる磁気回転不安定性)を数値計算から明らかにしたいと考えたとします。上述の方位角磁場を伴うトーラスの周囲に、静水圧平衡でない破茶滅茶なコロナ成分を置いてシミュレーションを行なったとしましょう。その研究をまとめて論文として提出すると、おそらくレフェリーからはこのようなコメントをいただくことができます。
これは本当にトーラスの中で発生した不安定性なのか?
トーラス成分以外にコロナ成分を加えることで、このコロナも運動を始めます。すると、このコロナの運動がトーラスのダイナミクスに多少なりとも影響を及ぼします。もし破茶滅茶なコロナ成分を置いて数値計算を行えば、それはもはやコロナの運動による影響が支配的な計算を行なったことになり、もはやトーラス中の不安定性を再現したものとは言えないのです。
このような理由から、数値シミュレーションでは平衡状態を初期条件として用います。あるいは、降着円盤数値計算コードのHARM(GitHub, 論文)ではトーラス周囲の空間に\(\rho_\mathrm{min} = 10^{-4} (r/r_\mathrm{in})^{-3/2}\)のような閾値を用いて埋めるということをしているようです。
トーラスの可視化
実際にJulia言語を用いてトーラスのガス密度分布などを計算し、それをカラーコントアとして可視化するソースコードを以下に示します。 ここではトーラス内には方位角磁場\(B_\varphi\)が存在するとした(12)式を用いました。計算に際して、方程式は全て規格化されているものとして、物理定数\(G, \mu, m_p, k_B\)は全て1としています。またこのときトーラスのパラメータはそれぞれ\(R_b = 5, a = 0, T_b = 0.01, \rho_b = 1, \Gamma = 4/3, \beta_b = 100\)などです。さらにこのトーラスを形成する重力ポテンシャルは擬ニュートンポテンシャルで与えられるとします。ここで\(r_g\)はシュバルツシルト半径で、この可視化では距離も規格化されていると考えて\(r_g = 0.01\)としています。 さらにトーラス中心の角運動量\(\ell_z\)は、(ガス圧勾配による力を無視した)ニュートンポテンシャルと遠心力の釣り合いから
\[\frac{\ell_z^2}{R_b^3} = \frac{GM}{R_b^2} \ \Longrightarrow \ \ell_z = \sqrt{GM R_b}\]と定めました。さらにコロナのパラメータは\(\rho_{c, 0} = 10^{-4}, T_c = 5\)としています。
using Plots
gr()
# compute gravitational potential Phi
function Phi(M, Rz)
R = Rz[1]
z = Rz[2]
r = sqrt(R ^ 2 + z ^ 2)
rg = 0.01
if r <= rg
Phi = - prevfloat(typemax(Float64))
else
Phi = - M / (r-rg)
end
return Phi
end
# compute effective Psib (= Psi @ (Rb, 0))
function Psib(inputs)
# decode from arguments
Gamma = inputs[1]
Tb = inputs[2]
rhob = inputs[3]
Rb = inputs[4]
betab = inputs[5]
M = inputs[6]
# compute effective potential Psib
Gamma1 = Gamma - 1
K = Tb / rhob ^ Gamma1
Csb2 = Gamma * K * rhob ^ Gamma1
H = 2 * K / (betab*Rb^(2*Gamma1))
vab2 = H * Rb ^ (2*Gamma1) * rhob ^ Gamma1
first = - lz ^ 2 / ((2*a-2)*Rb^2)
second = Phi(M, [Rb, 0])
third = Csb2 / Gamma1
forth = Gamma / (2*Gamma1) * vab2
return first + second + third + forth
end
# set input parameters for torus
Rb = 5
a = 0
Tb = 0.01
rhob = 1
Gamma = 1 + 1 / 3
betab = 10 ^ 2
M = 1
lz = sqrt(M * Rb)
# set input parameter for corona
Tc = 5
rhoc0 = 10 ^ (-4)
# set the number of grids
nR = 100
nz = 200
# set (R, z) cylindrical coordinates
Rmin = 0.01
Rmax = 15.01
zmin = -7.5
zmax = 7.5
Rs = range(Rmin, Rmax, length=nR)
zs = range(zmin, zmax, length=nz)
# encode to torus inputs
inputs = [Gamma, Tb, rhob, Rb, betab, M]
Gamma1 = Gamma - 1
K = Tb / rhob ^ Gamma1
###### main loop #####
rhos = []
emags = []
for z in zs
for R in Rs
# compute density
nume = Psib(inputs) - Phi(M, [R, z]) + lz ^ 2 * R ^ (2*a-2) / ((2*a-2)*Rb^(2*a))
deno = Gamma * K * (1+(R/Rb)^(2*Gamma1)/betab) / Gamma1
rho = (max(nume, 0)/deno) ^ (1/Gamma1)
# add hydrostatic equilibrium compotent
rhoc = rhoc0 * exp(-(Phi(M, [R, z])-Phi(M, [Rb, 0]))/Tc)
append!(rhos, log10(rho+rhoc))
# compute magnetic energy
emag = K * rho ^ Gamma / betab * (R/Rb) ^ (2*Gamma1)
append!(emags, log10(emag))
end
end
##### main loop end #####
# make density contour
contour(Rs, zs, rhos, fill=true, linewidth=0, levels=20,
aspect_ratio=:equal, xlim=[Rmin, Rmax], ylim=[zmin, zmax], xlabel="R", ylabel="z", title="Log(Density)", extend="both")
savefig("density.png")
# make magnetic energy contour
contour(Rs, zs, emags, c=:ice, fill=true, linewidth=0, levels=20,
aspect_ratio=:equal, xlim=[Rmin, Rmax], ylim=[zmin, zmax], xlabel="R", ylabel="z", title="Log(Magnetic Energy)")
savefig("magnetic_energy.png")
これを用いて可視化されたガス密度\(\rho\)、磁場のエネルギー密度(磁気圧)\(\frac{1}{8\pi} B_\varphi^2\)は以下のようになります。
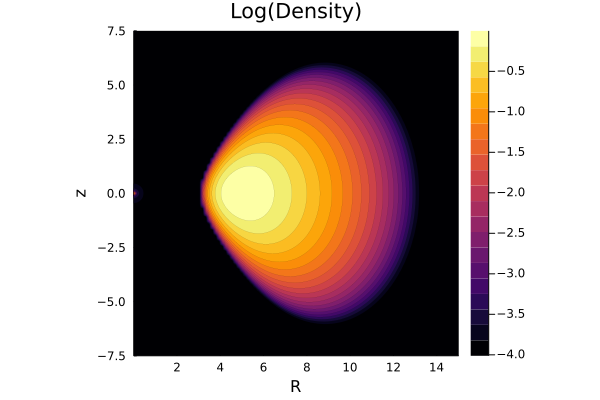
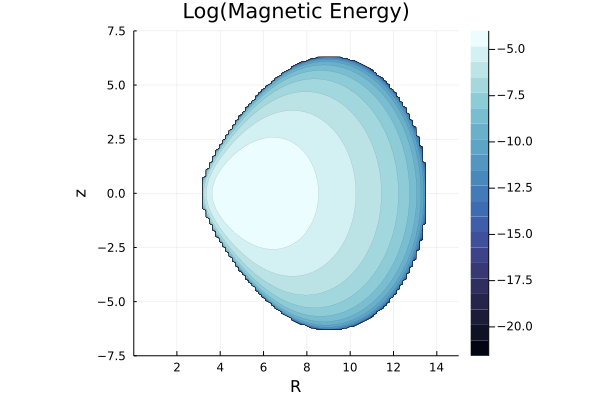
上述の数値計算コードのパラメータを適当に変化させて遊んでみると良いでしょう。例えばトーラス最深部の温度\(T_b\)を大きくすると、スケールハイトが大きくなることからトーラスが膨張します。
参考文献
[1] Okada et al., 1989, “A Model of Astrophysical Tori with Magnetic Fields”
[2] Kato et al., 2004, “Magnetohydrodynamic Accretion Flows: Formation of Magnetic Tower Jet and Subsequent Quasi-Steady State”
[3] Nishikori et al., 2006, “Global Three-dimensional Magnetohydrodynamic Simulations of Galactic Gaseous Disks. I. Amplification of Mean Magnetic Fields in an Axisymmetric Gravitational Potential”
[4] Hayashi et al., 1996, “X-Ray Flares and Mass Outflows Driven by Magnetic Interaction between a Protostar and Its Surrounding Disk”
[5] Kudoh et al., 2002, “Are Jets Ejected from Locally Magnetized Accretion Disks?”
[6] Gammie et al., 2003, “HARM: A Numerical Scheme for General Relativistic Magnetohydrodynamics”