Table of contents

HLL法
参考文献

HLL法

ここでは(磁気)流体力学の計算手法であるHarten-Lax-van Leer (略してHLL)法についての勉強メモを記述しています。

磁気流体方程式群

数値計算のために、質量保存の式(連続の式)、運動量保存則、エネルギー保存則、誘導方程式を一つにまとめましょう。以下では\(x\)方向の一次元のみを考えることとします。さらにあらかじめこれらの方程式は規格化されているものとすると

\[\frac{\partial \mathbf{U}}{\partial t} + \frac{\partial \mathbf{F}}{\partial x} = \mathbf{0} \tag{1}\]

のように書くことができます。ここで

\[\mathbf{U} = \left( \begin{array}{c} \rho \\ \rho v_x \\ \rho v_y \\ \rho v_z \\ E \\ B_x \\ B_y \\ B_z \end{array}\right) \tag{2}\]

は保存量ベクトル、そして

\[\mathbf{F} = \left( \begin{array}{c} \rho v_x \\ \rho v_x v_x + P_\mathrm{tot} - B_x^2 \\ \rho v_y v_x - B_y B_x \\ \rho v_z v_x - B_z B_x \\ (E + P_\mathrm{tot}) v_x - (\mathbf{B}\cdot \mathbf{v}) B_x \\ 0 \\ B_y v_x - v_y B_x \\ B_z v_x - v_z B_x \end{array} \right) \tag{3}\]

は流体による流束ベクトルです。\(P_\mathrm{tot} = P + \frac{1}{2} B^2\)はガス圧と磁気圧を足し合わせた全圧力です。さらに今回は外力などは無視しています。また一次元の場合には\(B_x\)は時間変化しません。さらに磁場の発散が0であることから\(\nabla \cdot \mathbf{B} = \frac{\partial B_x}{\partial x} =0\)、すなわち\(B_x = (一様)\)であることもわかります。よってこの問題設定では磁場は時間・空間に依存せず一定の値を持ちます。

流束計算

物理的導出

厚さが無視できる面積\(\Delta S\)仕切りを挟んで左側の状態を\(L\)(left)、右側の状態を\(R\)(right)のように記述しましょう。ここから仕切りを取り除いたときの\(\Delta t\)後の状態ついて考えます。これをリーマン問題と呼びます。仕切りを取り除いた瞬間、左側と右側で密度や圧力が異なるため、波動が発生します。1次元なので、この波動は左方向と右方向の2つの方向にしか進まないはずです。このとき、左方向・右方向に進む波の伝播速度をそれぞれ \(S_L, S_R\)のように書きましょう。すると下図のように左に進む波面と右に進む波面、そしてその間に中間状態が生まれます。この中間状態はアスタリスク\((\ast)\)をつけて表現することにしましょう。すると以下のように図示することができます。

ここで左側・中間状態・右側の領域における流束をそれぞれ\(\mathbf{F}_L, \mathbf{F}^\ast, \mathbf{F}_R\)のように書くことにします。また\(\Delta t\)は非常に小さく、この間は中間状態\(\mathbf{U}^\ast, \mathbf{F}^\ast\)は一定と扱って良いものとします。右パネルの右側部分に伝播した部分に注目したとき、\(S_R\)の速度で伝播する波面を通した保存則から

\[S_R \mathbf{U}_R - \mathbf{F}_R = S_R \mathbf{U}^\ast - \mathbf{F}^\ast \tag{4}\]

が導かれます。この式の両辺に\(\Delta t\)とこの管の断面積である\(\Delta S\)をかければ、その意味を理解することができます。

\[S_R \Delta t \Delta S \mathbf{U}_R - \Delta t \Delta S \mathbf{F}_R = S_R \Delta t \Delta S \mathbf{U}^\ast - \Delta t \Delta S \mathbf{F}^\ast \tag{5}\]

\(S_R \Delta t\)は右側に波が進んだ距離です。ここに\(\Delta S \mathbf{U}_R\)をかければ、これはこの領域に元々あった右側領域の物理量の合計(例えばガスによる質量の総量など)になります。\(\Delta t\)の間に面積\(\Delta S\)の波面を通して流束\(\mathbf{F}_R\)で出ていく分が\(-\Delta t \Delta S F_R\)となります。同様に、\(\Delta t\)後にはこの領域は\(\mathbf{U}^\ast\)で満たされています。よってこの領域の物理量の合計は\(S_R \Delta t \Delta S \mathbf{U}^\ast\)になります。そして波面を通して\(-\Delta t \Delta S F^\ast\)のやり取りが行われます。外力などが存在しないため、これらが保存することから、(5)式の等号が成り立ちます。
同様のことを左側についても考えると

\[S_L \mathbf{U}_L - \mathbf{F}_L = S_L \mathbf{U}^\ast - \mathbf{F}^\ast \tag{6}\]

(4), (6)式より\(F^\ast\)を消去すると

\[\mathbf{U}^\ast = \frac{S_R \mathbf{U}_R - S_L \mathbf{U}_L - \mathbf{F}_R + \mathbf{F}_L}{S_R - S_L} \tag{7}\]

これを(4)式に再び代入して整理すれば

\[\mathbf{F}^\ast = \frac{S_R \mathbf{F}_L - S_L \mathbf{F}_R + S_R S_L (\mathbf{U}_R - \mathbf{U}_L)}{S_R - S_L} \tag{8}\]

数学的導出

以下では数学的な証明方法を示します。以下のような時空図上で考えましょう。

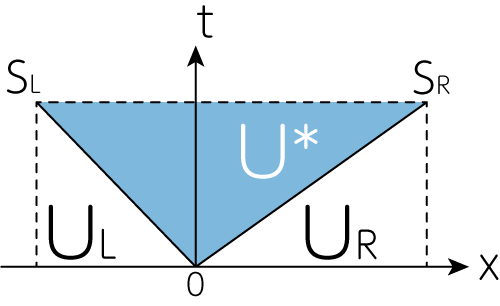
先程と同様の状況を考えていますが、今回は仕切りの位置を\(x=0\)として描いています。(1)式をこの時空図平面上での面\(A\)で面積積分すると、グリーンの定理より一般に

\[\iint_A \left( \frac{\partial \mathbf{U}}{\partial t} + \frac{\partial \mathbf{F}}{\partial x}\right) dt dx = \oint_C (-\mathbf{F} dt + \mathbf{U} dx) = 0 \tag{9}\]

が成り立ちます。ここで\(C\)は面\(A\)を囲むような閉曲線です。このときこの周回積分に下図の左パネルのような経路を選べば(4)式が、下図右パネルのような経路を選べば(6)式を得ることができます。

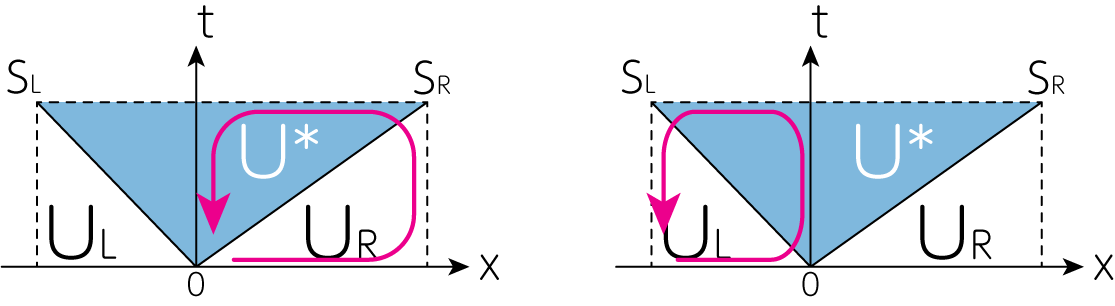
注意: 暗黙のうちに\(S_L < 0\)を仮定しているので符号に注意が必要です。

数値計算に用いる

実際の数値計算では\(S_L, S_R\)の大きさを考慮する必要があります。もし\(S_R < 0\)ならば、仕切りを通過する流束は\(\mathbf{F}_R\)になります。同様に\(S_L >0\)ならば、用いる流速は\(\mathbf{F}_L\)でなければなりません。下図は左から順に\(S_L > 0, S_L \leq 0 < S_R, S_R \leq 0\)の場合を図示したものです。

以上より、数値計算を行う場合、その流束の選択は

\[\mathbf{F}_\mathrm{HLL} = \left\{ \begin{array}{ll} \mathbf{F}_L & \mathrm{if} \ S_L > 0 \\ \mathbf{F}^\ast & \mathrm{if} \ S_L \leq 0 < S_R \\ \mathbf{F}_R & \mathrm{if} \ S_R \leq 0 \end{array}\right. \tag{10}\]

のようになります。もしくは\(S_R = \max (S_R, 0), S_L = \min(S_L, 0)\)のように定めておけば

\[\mathbf{F}_\mathrm{HLL} = \frac{S_R \mathbf{F}_L - S_L \mathbf{F}_R + S_R S_L (\mathbf{U}_R - \mathbf{U}_L)}{S_R - S_L} \tag{11}\]

だけで計算することも可能です。

発展: 中間状態の多重化

ここまでは右と左に進む波が1つずつ、そしてその間に挟まれた中間状態も1つとしました。しかし、実際の流体力学の方程式の固有値には以下のようなものが存在します。

右に進む波: \(S_R = v_x + C_s\)
左に進む波: \(S_L = v_x - C_s\)
流体の運動: \(S_M = v_x\)

ここで簡単のために\(C_s > v_x > 0\)としました。ここからわかるように、左右に速く進む波ともう一つ、流体の運動により伝播する波が存在します。この波の波面を挟んで右側と左側でも状態の変化が起こるため、中間状態を1つとした近似よりも、実際には下図のように2つの中間状態を用いた方がより流体力学系を再現できそうです。このような手法をHLLC法(“C”はcontact, つまり接触不連続面の意味)と呼びます。

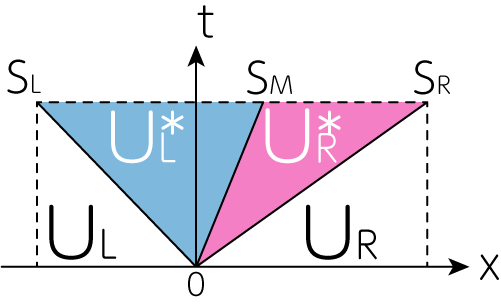
さらに磁気流体に至っては、速い磁気音波・遅い磁気音波、そして普通のアルヴェーン波まで存在します。これらの速度で伝わる波面をはさんだ状態変化を考慮する手法も存在します。これらについては後ほどご説明したします。

HLL流束の計算モジュール

以下にHLL流束計算コードのJulia実装例を示します。

using LinearAlgebra    
include("../convert/convert.jl")
include("../const/const.jl")
function hll!(F::Array{Float64, 2}, Vl::Array{Float64, 2}, Vr::Array{Float64, 2}, nxmax::Int64)
    for i in 1:nxmax-1
        # compute B * B of left side
        bl2 = dot(Vl[6:8, i], Vl[6:8, i])
        # compute v * B of left side
        vlbl = dot(Vl[2:4, i], Vl[6:8, i])
        # convert Vl ---> Ul
        Ul = Convert.v_to_u(Vl[:, i])
        # convert Ul, VL ---> Fl
        Fl = Convert.uv_to_f(Ul, Vl[:, i], bl2, vlbl)
        # compute fast-mode speed of left side
        gmprl = gm * Vl[5, i]
        vfl = sqrt(((bl2+gmprl)+sqrt((bl2+gmprl)^2-4*gmprl*Vl[6, i]^2))/(2*Vl[1, i]))
        # compute B * B of right side
        br2 = dot(Vr[6:8, i], Vr[6:8, i])
        # compute v * B of right side
        vrbr = dot(Vr[2:4, i], Vr[6:8, i])
        # convert Vr ---> Ur
        Ur = Convert.v_to_u(Vr[:, i])
        # convert Ur, Vr ---> Fr
        Fr = Convert.uv_to_f(Ur, Vr[:, i], br2, vrbr)
        # compute fast-mode speed of right side
        gmprr = gm * Vr[5, i]
        vfr = sqrt(((br2+gmprr)+sqrt((br2+gmprr)^2-4*gmprr*Vr[6, i]^2))/(2*Vr[1, i]))
        # compute sl, sr
        sl = min(min(Vl[2, i], Vr[2, i])-max(vfl, vfr), 0.0)
        sr = max(max(Vl[2, i], Vr[2, i])+max(vfl, vfr), 0.0)
        # compute HLL flux
        for m in 1:8
            F[m, i] = (sr*Fl[m]-sl*Fr[m]+sr*sl*(Ur[m]-Ul[m])) / (sr-sl)
        end
    end
end

あらかじめ保存量ベクトル\(\mathbf{U}\)や基本変数ベクトル\(\mathbf{V}\)から流束ベクトルを計算するconvert.jlなどを作成しておきます。またconst.jlには比熱比\(\gamma\)などが定義されています。コード途中に出てくるUl, Vl, Flは左側の物理量における保存量、基本変数、流束ベクトルを表し、Ur, Vr, Frは右側のものを意味します。