白色矮星

ここでは、コンパクト天体の1つである白色矮星の特徴をまとめています。

観測的特徴

白色矮星は、初期質量が\(\sim 8 M_\odot\)より小さい恒星が、AGB段階で水素を多く含む外層のほとんどを失い中心核だとなった恒星です。そのため、核融合反応は起こしていません。内部は電子の縮退圧で支えられており、構造は温度にほとんど依存しないことから、重力収縮をせずにゆっくりと冷えつつある段階です。電子の縮退した中心核では、電子による熱伝導が非常に良いため、ほぼ等温になっています。その外側に薄いヘリウムの層と水素の層が存在し、その中で温度が中心温度\((10^6 \sim 10^8 \mathrm{K})\)から表面温度へと変化します。この薄い外挿は、中心核の温度を保つブランケットのはたらきをします。
白色矮星の進化経路 (cooling sequence) は、HR図上で、高温で明るい惑星状星雲中心核領域から主系列の高温側に主系列とほぼ平行に、暗く温度が低い領域へと伸びています。

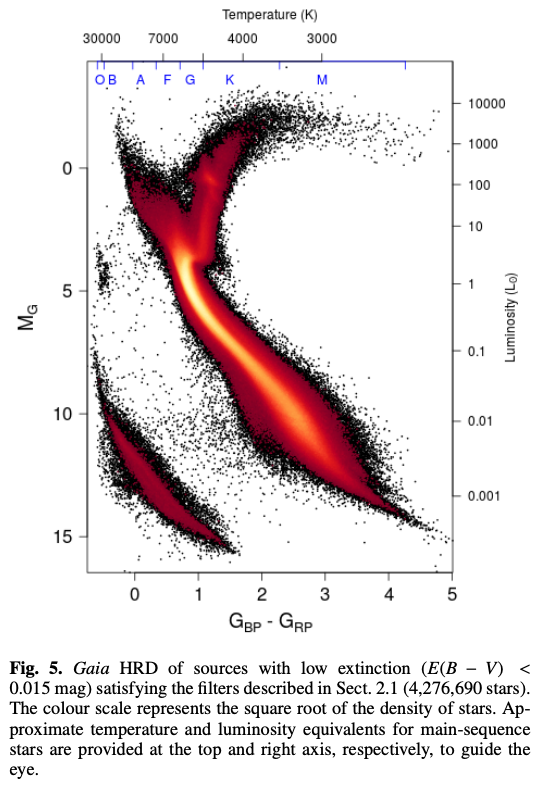
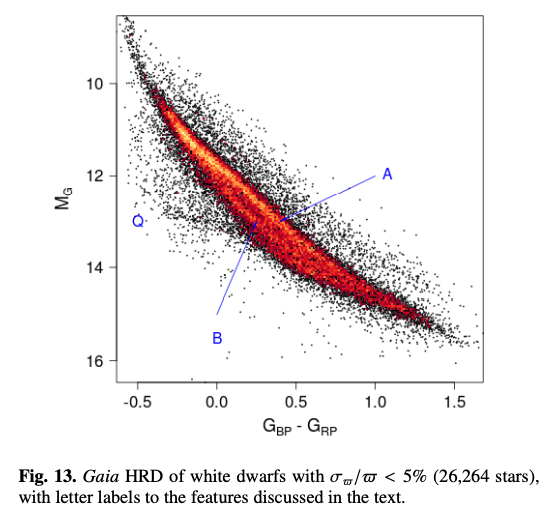
Gaia Collaboration (2018)より。上図はHR図全体、下図は白色矮星部分のみを拡大したもの。

白色矮星の典型的な半径は\(\sim 10^{-2} R_\odot\)で、典型的な表面温度は\(\sim 4 \times 10^3 \sim 10^5 \mathrm{K}\)の範囲を持ちます。典型的な質量は\(\sim 0.6 M_\odot\)で、平均密度は太陽の\(10^6\)倍程度になります。また表面重力は\(\log g \sim 8\)です。
白色矮星の自転は遅く、自転周期は数時間以上です。太陽が仮に角運動量を保存したまま白色矮星サイズになったとすると、自転周期は数分程度になるはずです。このことは、主系列星から白色矮星に至る進化の途中で、角運動量の多くが失われてなくてはならないことを意味します。
また、白色矮星には周期\(100 \sim 10^3\)秒で変光を示すものが多くあります。これは、白色矮星の薄い外層の非動径方向のgモード振動によるもので、その観測から質量・自転周期・水素外層の厚さ・冷却時間スケールなどの情報を引き出すことができます。
また白色矮星の10%以上が、\(10 \mathrm{KG} \sim 10^9 \mathrm{G}\)の磁場を持つことが知られています。
白色矮星は、DA, DB, DC, DO, DZ, DQのようにスペクトル分類されます。

DA: 水素のバルマー線だけが観測され、ヘリウムや金属線は観測されません。白色矮星の80%凍度がDA型白色矮星に分類されます。強い重力により最も軽い水素が浮き上がり、純粋に近い水素の層を作っています。その層の厚さは\(10^{-4} M_\odot\)以下であり、その下には純粋に近いヘリウムの層が存在すると推測されています。
DB: 中性ヘリウムのスペクトル線が強く、水素または金属の輝線は観測されません。つまり、この白色矮星の大気はほぼ純粋なヘリウムで構成されています。全体の約20%がDB型白色矮星です。白色矮星のほとんどはDA, DBに分類されます。
DC: 連続スペクトルで、目立つ輝線が見られないのが特徴です。
DO: HeIIのスペクトル輝線が支配的に見られます。これは高温\((T \sim 10^5 \mathrm{K})\)の白色矮星です。
DZ: 金属による輝線だけが観測されます。
DQ: 炭素、または炭素を含む分子のスペクトル線が見られます。

その他にも、以下のような記号が用いられます。

P: 偏光が観測される強磁場白色矮星です。
H: 偏光が観測されない強磁場白色矮星です。
X: 特異なスペクトルや、分類不能なものを、Xと表します。
E: 輝線が見られます。
?: 分類が不確定なものを表します。
V: 変光をする場合に記載される記号です。

白色矮星の表面元素組成は、対流外層の勢力や水素の浮揚効果により、白色矮星進化の途中でも変化する場合があります。比較的温度の低い白色矮星では、(周囲の水素をイオン化しないため)星間物質からの降着 (\(\sim 10^{-17} M_\odot / \mathrm{yr}\))を受け、それによる表面元素組成変化の効果も重要となる可能性もあります。 \(T_\mathrm{eff}\)が30000-45000Kの領域はDBギャップと呼ばれ、その領域ではDB型白色矮星は存在しません。それはわずかに外層に混合していた水素が浮き上がってきて、表面に純粋な水素の層を形成するためと考えられています。 30000Kよりも低くなると、\({}^+ \mathrm{He}\)の不完全電離層により対流が発生します。すると水素層が薄い場合は混合から表面がほとんどヘリウムとなり、DB型白色矮星となります。
比較的\(T_\mathrm{eff}\)の低い領域では、DA型白色矮星の割合が表面温度が下がるほど小さくなる傾向にあります。これは、低温になると水素電離に伴う表面対流層が発達するためです。水素の層が薄いものほど高い表面温度で、下のヘリウム層との混合が起こり、水素層が薄い場合は水素の層がなくなるためと推測されます。

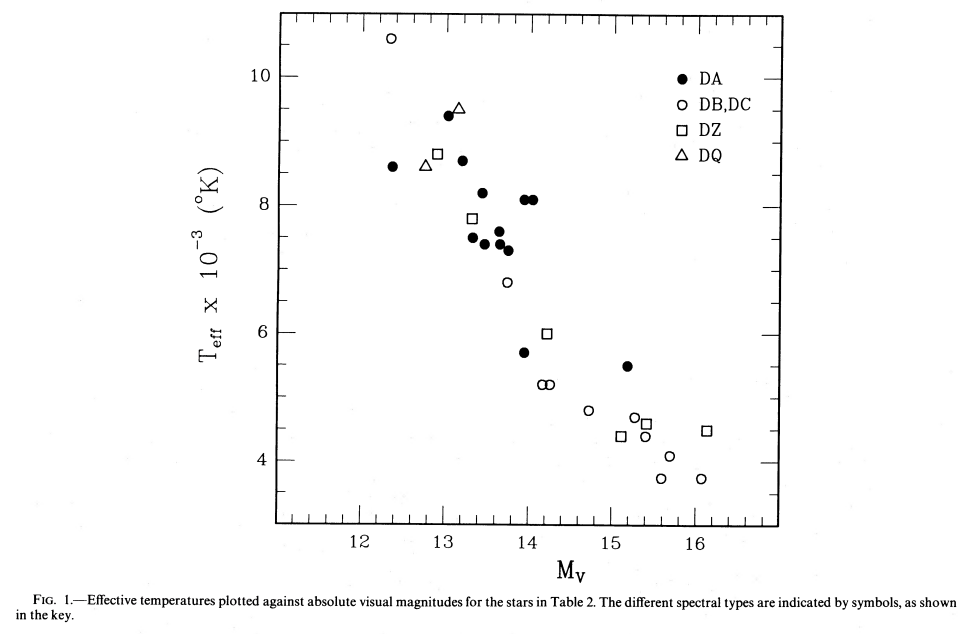
Liebert et al. (1988)より。白色矮星の有効温度分布を示したもの。

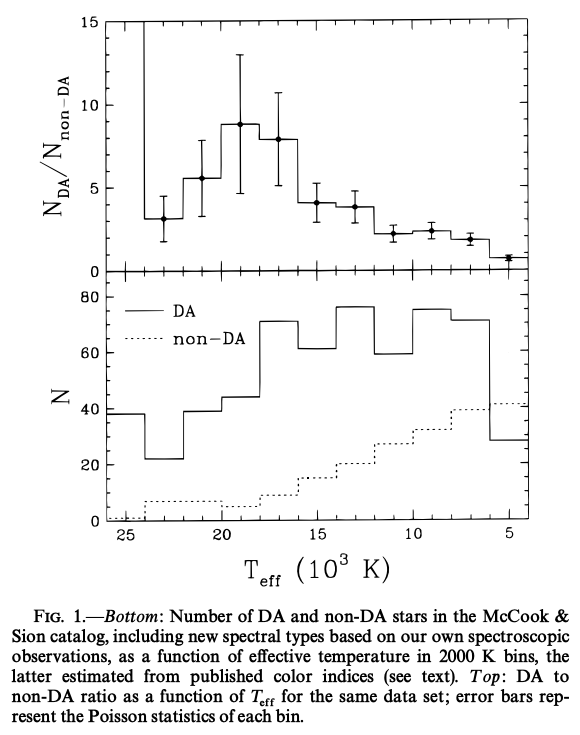
Bergeron et al. (1997)より。DA型とそうでないものの、有効温度に対する頻度分布。

質量-半径関係

白色矮星の質量と半径の関係は、電子の縮退とチャンドラセカール限界質量のページをご覧ください。これによると、白色矮星の限界質量は

\[M_\mathrm{Ch} = 1.46 \left( \frac{2}{\mu_\mathrm{e}}\right)^2 M_\odot\]

のようになります。
しかしこの議論では、原子核の効果が無視されています。実際の白色矮星内部では、原子核の電荷はその静電場により電子を引き寄せるため、電子の自由な運動を妨げる効果を持ちます。そのため、原子核の効果を無視した場合に比べ圧力は小さくなり、ある質量に対する白色矮星の半径も小さくなります。この効果は、白色矮星を構成する原子核が重たい原子核であるほど、大きくなります。

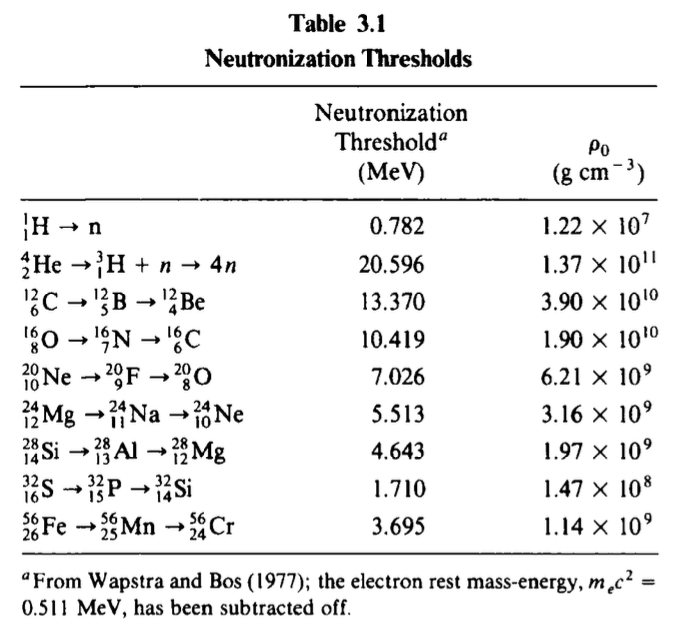
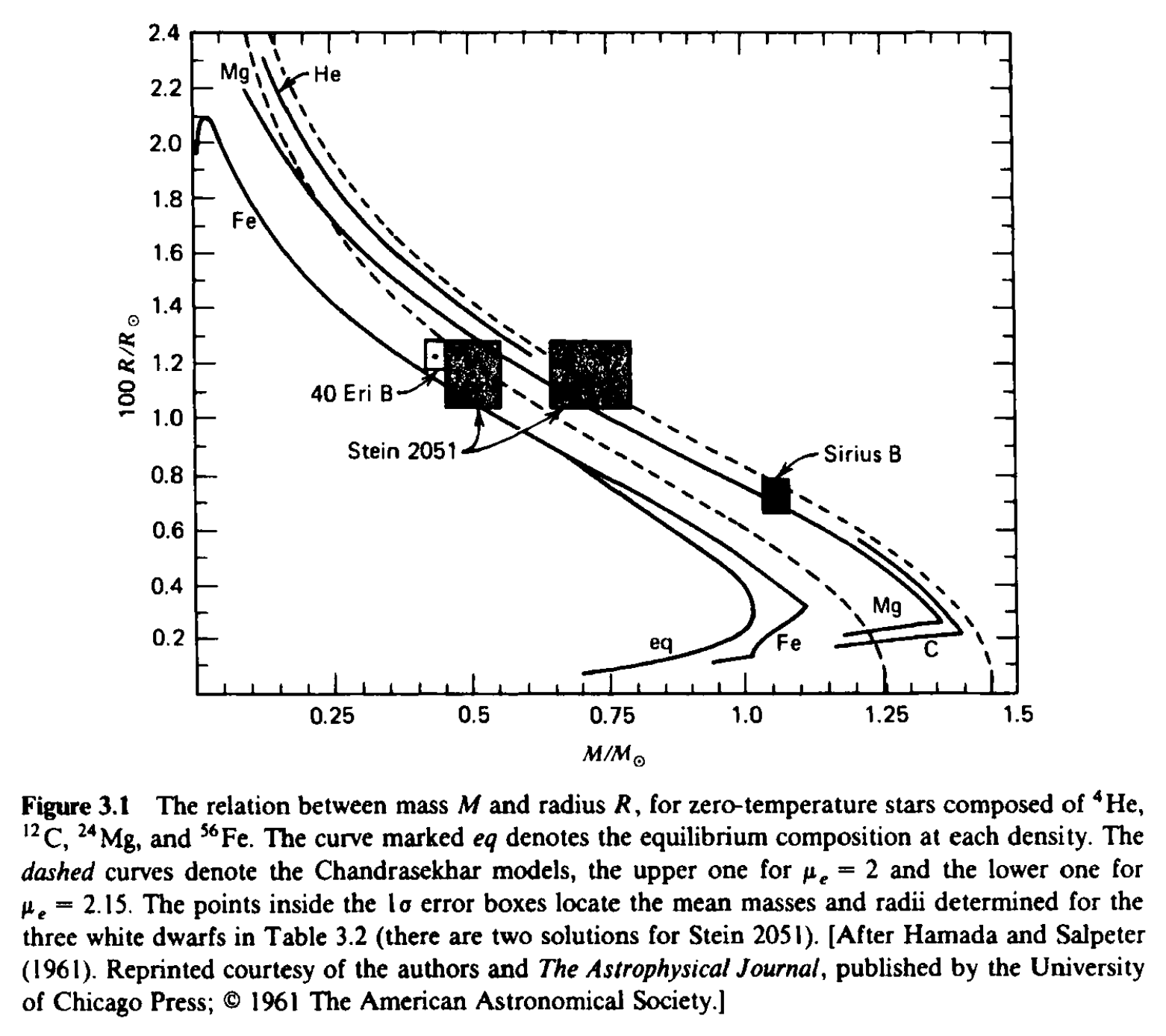
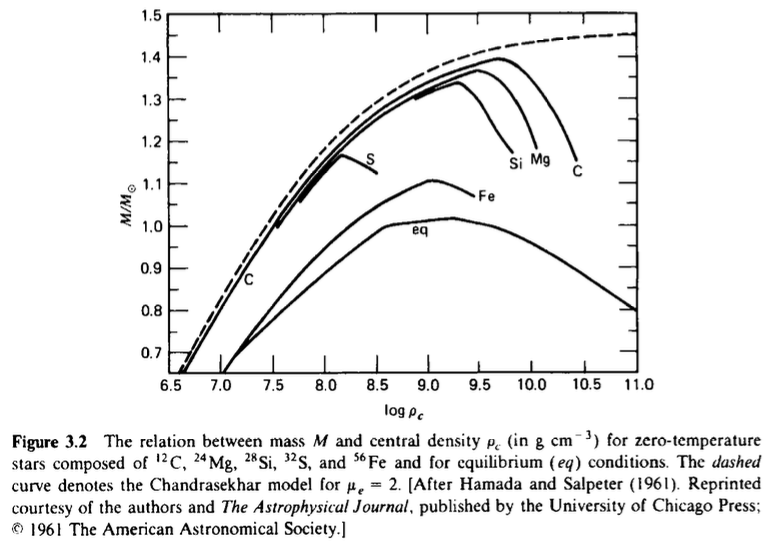
Shapiro & Teukolsky, “Black Holes, White Dwarfs, and Neutron Stars”より。上表は、各種原子核が中性子化あるいは中性子過剰原子核になるのに必要なエネルギーと質量密度。真ん中図は、実際に観測されている白色矮星を、質量-半径の図にプロットしたもの。実線はゼロ温度での\({}^{4} \mathrm{He}, {}^{12} \mathrm{C}, {}^{24} \mathrm{Mg}, {}^{56} \mathrm{Fe}\)からなるモデルでの質量-半径関係の曲線。下図は真ん中図と同じものを、横軸を密度の対数、縦軸を質量にしたもの。

白色矮星の質量が増加し、限界質量近くになったとしましょう。すると密度が非常に大きいため、温度が低くても種々の原子核反応が起こります。中心付近に炭素が含まれている場合、\(\rho \gtrsim 10^{10} \mathrm{g/cm^3}\)になると\({}^{12} \mathrm{C} + {}^{12} \mathrm{C}\)の反応が爆発的に起こり、Ia型超新星爆発が起こります。このとき、星の全エネルギーが正となり、星全体が飛び散ってしまいます。また炭素がなくO, Ne, Mgなどからなる場合は、電子が原子核に取り込まれ、中性子過剰な原子核になっていきます。このとき、圧力を担っている電子の数が減少するため、収縮が起こりさらに電子捕獲が進みます。そのため、白色矮星はつぶれ、中性子星になります。

質量分布

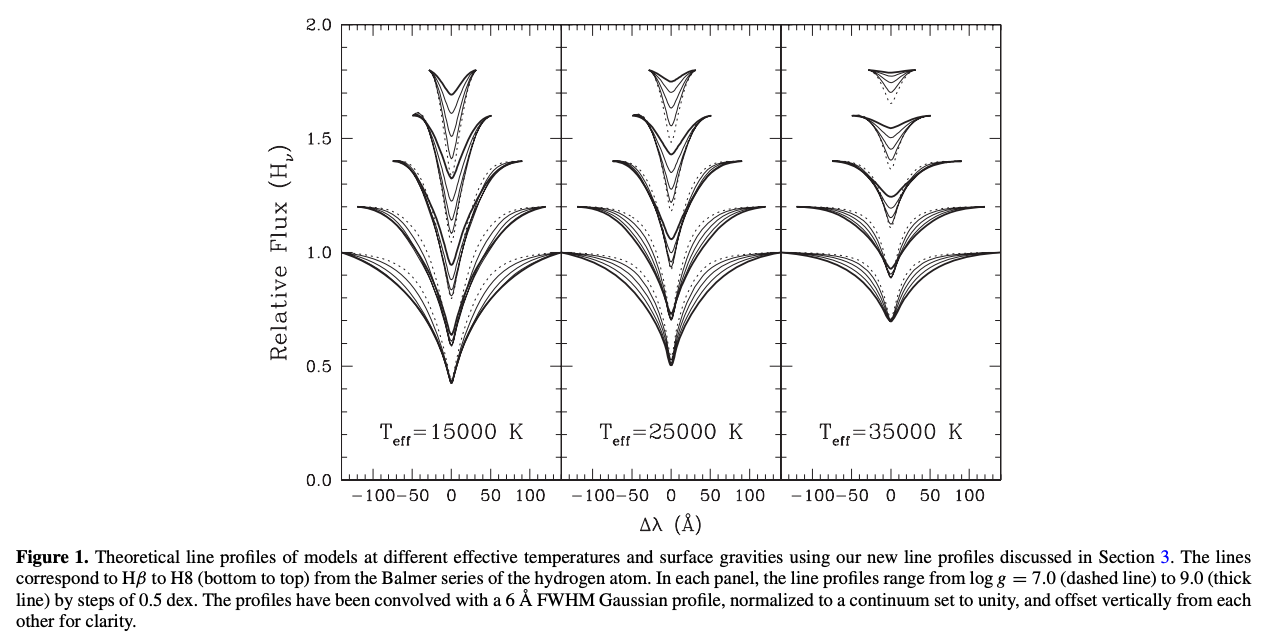
連星系を構成していない単独の白色矮星の質量は、水素バルマー線の形状を用いて評価されます。白色矮星のスペクトル線は、白色矮星大気の密度が高いために周囲の粒子からの摂動によって広がっています (pressure broadening。) 光球面での密度は重力が強いほど大きくなるため、スペクトル線の幅を理論的に計算された形状と比較することで、表面重力\(g\)の値を知ることができます。

Tremblay & Bergeron (2009)より

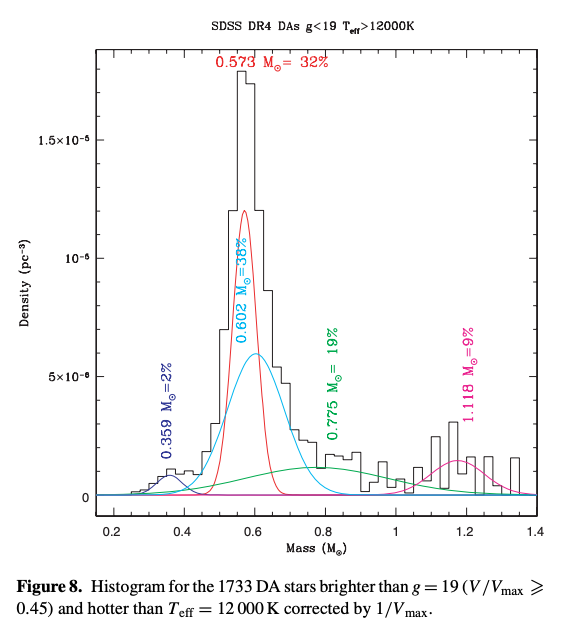
\(g = GM / R^2\)より、先ほどの質量-半径関係を用いれば、質量を求めることができます。このようにして求められた白色矮星の質量に対する頻度分布は、\(\sim 0.6 M_\odot\)に鋭いピークを持ちます。これは、AGB段階で中心核の質量が\(\sim 0.6 M_\odot\)に対応する光度になると、非常に強い恒星風により外層が飛ばされてしまうことを示唆しています。また\(\sim 0.4 M_\odot\)あたりの小さなピークは、近接連星進化における質量交換によってできたと考えられています。次の図は、SDSSのデータから求められたDA型白色矮星の質量分布 (volume limitted)を表しています。

Kepler et al. (2007)より

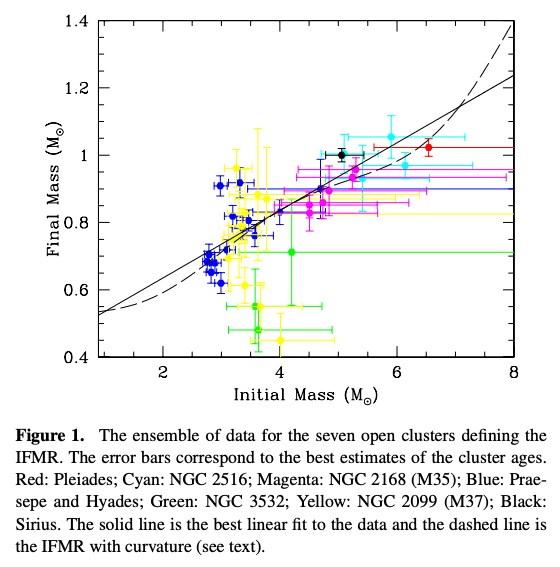
そして次の図は、白色矮星の質量とそれが主系列星だった時点での質量との関係 (initial-to-final mass relation)を表します。この関係は非常に不確定ですが、銀河内の散開星団中の白色矮星の質量 (\(\log g\)から求められたもの)と、主系列転向質量 (turn-off mass)との関係などから、経験的に求められたものです。図の直線は最小2乗法により求められたもので、曲線は白色矮星の質量分布と population synthesis model を用いて得られたものです。

Ferrario et al. (2005)より

また質量放出率の光度や半径依存性に適当な式を仮定して計算された、主系列星から白色矮星までの進化モデルによってもinitial-to-final mass relationが得られます。しかし白色矮星が連星系中にある場合、質量移動・降着が起こる場合があることに注意が必要です。

参考文献

[1] Gaia Collaboration, 2018, “Gaia Data Release 2: Observational Hertzsprung-Russell diagrams”
[2] Liebert & Sion, 1994, “The Spectroscopic Classification of White Dwarfs: Unique Requirements and Challenges”
[3] Liebert et al., 1988, “The Luminosity Function of White Dwarfs”
[4] Bergeron et al., 1997, “The Chemical Evolution of Cool White Dwarfs and the Age of the Local Galactic Disk”
[5] Tremblay & Bergeron, 2009, “Spectroscopic Analysis of DA White Dwarfs: Stark Broadening of Hydrogen Lines Including Nonideal Effects”
[6] Kepler et al., 2007, “White dwarf mass distribution in the SDSS”
[7] Ferrario et al., 2005, “The open-cluster initial-final mass relationship and the high-mass tail of the white dwarf distribution”
[8] Shapiro & Teukolsky, “Black Holes, White Dwarfs, and Neutron Stars”