Table of contents
磁力線の可視化
磁気流体計算では磁力線を可視化することで、磁場が流体に及ぼす力(磁気張力, 磁気圧勾配力)をわかりやすくすることができます。 それは磁力線だけに限らず、例えば流線を可視化することにより流れの様子が見やすくなり、より理解が捗ることが期待されます。 ここでは磁気流体の磁力線を可視化することを考えていきましょう。
磁力線 = 磁場ベクトルを接ベクトルに持つ曲線
磁力線とはすなわち、下図のように磁場ベクトルを接ベクトルに持つような曲線のことです。
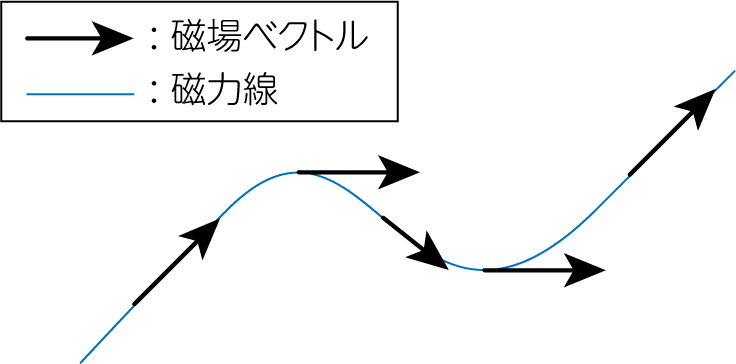
\(xy\)平面内において、接線の傾きが磁場ベクトルの方向に一致するような曲線を求めましょう。この曲線が満たす方程式は、磁場ベクトルを\(\mathbf{B} = (B_x, B_y)\)とすると
\[\frac{dy}{dx} = \frac{B_y}{B_x} \tag{1}\]のようになります。
ベクトルポテンシャルによる変形
マクスウェル方程式において、磁場は常にその発散が0であることが知られています。ここから磁場はベクトルポテンシャル\(\mathbf{A}\)を用いて
\[\mathbf{B} = \nabla \times \mathbf{A} = \left( \begin{array}{c} \frac{\partial}{\partial x} \\ \frac{\partial}{\partial y} \\ \frac{\partial}{\partial z} \end{array} \right) \times \left( \begin{array}{c} A_x \\ A_y \\ A_z \end{array}\right) = \left( \begin{array}{c} \frac{\partial A_z}{\partial y} - \frac{\partial A_y}{\partial z} \\ \frac{\partial A_x}{\partial z} - \frac{\partial A_z}{\partial x} \\ \frac{\partial A_y}{\partial x} - \frac{\partial A_x}{\partial y} \end{array} \right) \tag{2}\]今は2次元の問題を考えているため、\(\frac{\partial}{\partial z} = 0\)とすると
\[B_x = \frac{\partial A_z}{\partial y}, \quad B_y = - \frac{\partial A_z}{\partial x} \tag{2}\]となります。(2)式を(1)式に代入すると
\[\frac{dy}{dx} = \frac{- \frac{\partial A_z}{\partial x}}{\frac{\partial A_z}{\partial y}} \ \Longrightarrow \ \frac{\partial A_z}{\partial y} dy = - \frac{\partial A_z}{\partial x} dx\]のように変形することができます。両辺を不定積分しましょう。積分定数をまとめて右辺に持っていくと
\[A_z = -A_z + C \ \Longrightarrow \ A_z = C' \tag{3}\]すなわち、\(xy\)平面上の磁力線は、ベクトルポテンシャルの\(z\)成分の等値線に等しいことがわかりました。
実際に描画してみよう
出力された磁場のみから計算を行う場合
実際に描画するためには、\(A_z\)を計算しておかなければなりません。(2)式より
\[A_z(x, y) = \int_0^y B_x(x, y') dy', \quad A_z(x, y) = - \int_0^x B_y (x', y) dx'\]となります。\(B_x, B_y\)両方の寄与を含めるために
\[A_z = \frac{1}{2} \left( \int_0^y B_{x} (x, y') dy' - \int_0^x B_y(x', y) dx'\right) \tag{4}\]のようにして計算をすれば、\(xy\)平面内で\(B_x, B_y\)の両方が存在する場合の磁力線を可視化することが可能です。
ベクトルポテンシャルの時間発展を計算する場合
またもう一つの方法として、磁気流体計算中\(A_z\)の時間発展を計算する手法があります。(2)式と理想磁気流体の誘導方程式より
\[\frac{\partial \mathbf{B}}{\partial t} = \nabla \times \frac{\partial \mathbf{A}}{\partial t} = \nabla \times (\mathbf{v} \times \mathbf{B}) \ \Longrightarrow \ \frac{\partial \mathbf{A}}{\partial t} = \mathbf{v} \times \mathbf{B} \tag{5}\]となります。これを離散化すれば、\(n+1\)ステップ目の時刻での\(i\)番目のセルにおけるベクトルポテンシャルは
\[\mathbf{A}^{n+1}_i = \mathbf{A}^{n}_i + (\mathbf{v}^n_i \times \mathbf{B}^n_i)\]のように求めることができます。べクトルポテンシャル自体は磁気流体計算に用いることが無くても、このように時間発展を計算すれば(先程のように積分計算の誤差を含めることなく)より正確に磁力線を描くことが可能です。
べクトルポテンシャルを用いることで磁場の発散を常にゼロに保つ方法を用いる方法を採用している場合には、それを流用すれば良いでしょう。
可視化結果
2次元磁気流体計算を実施した結果から、実際に磁力線を可視化した結果を以下に示します。斜め45度方向に強い磁場がある中で爆風波が広がっていく様子を計算したものです。
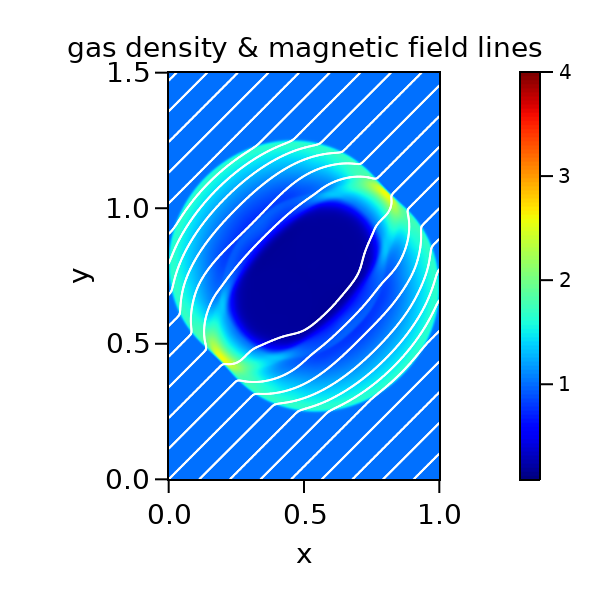
伝播する衝撃波が磁力線を押し退ける様子が見られます。磁気流体力学では、磁力線があたかも物理的実体を持つかのように振る舞います。 磁力線は磁気張力や磁気圧勾配によりプラズマに力を及ぼすため、磁力線の可視化は磁気流体現象の理解に役立てることができます。