Table of contents
ポアソン方程式 (Poisso equation)
ここでは分布関数\(f(\mathbf{x}, \mathbf{v})\)を用いて、重力場を決定する方程式であるポアソン方程式を導出しましょう。
普通のポアソン方程式の導出

上図のように、位置\(\mathbf{x}'\)にある質量密度\(\rho(\mathbf{x}')\)が、位置\(\mathbf{x}\)に作る重力ポテンシャルは
\[\Phi (\mathbf{x}) = - G \int \frac{\rho(\mathbf{x}')}{\vert \mathbf{x}' - \mathbf{x} \vert} d\mathbf{x}' \tag{1}\]のように書かれます。これの勾配は
\[\frac{\partial \Phi}{\partial \mathbf{x}} = - G \int \rho(\mathbf{x}') \frac{\partial}{\partial \mathbf{x}} \left( \frac{1}{\vert \mathbf{x}' - \mathbf{x} \vert} \right) d\mathbf{x}' = - G \int \rho(\mathbf{x}') \frac{\mathbf{x}' - \mathbf{x}}{\vert \mathbf{x}' - \mathbf{x} \vert^3} d\mathbf{x}' = - \mathbf{F} \tag{2}\]のように計算されます。 最後の\(\mathbf{F} = - \frac{\partial \Phi}{\partial \mathbf{x}}\)は重力により位置\(\mathbf{x}\)に働く力を表します。 さらにこれの発散を取ると
\[\nabla \cdot \mathbf{F} = \nabla \cdot \left( - \frac{\partial \Phi}{\partial \mathbf{x}}\right) = - \nabla^2 \Phi = G \int \rho(\mathbf{x}') \frac{\partial}{\partial \mathbf{x}} \cdot \left( \frac{\mathbf{x}' - \mathbf{x}}{\vert \mathbf{x}' - \mathbf{x} \vert^3}\right) d\mathbf{x}' \tag{3}\]この式の\(\mathbf{x}'\)での積分を実行しましょう。\(\mathbf{x}' \neq \mathbf{x}\)のときには、この積分値は0となります。 \(\mathbf{x}' = \mathbf{x}\)の積分値を求めるために、\(\mathbf{x}'\)が\(\mathbf{x}\)近傍の範囲\(h\)の中のみを考えましょう。 このとき\(\rho (\mathbf{x}') \simeq \rho (\mathbf{x}) = (一定)\)と考えることができます。よって
\[\nabla^2 \Phi = - G \rho (\mathbf{x}) \int_{\vert \mathbf{x}' - \mathbf{x}\vert \leq h} \frac{\partial}{\partial \mathbf{x}} \cdot \left( \frac{\mathbf{x}' - \mathbf{x}}{\vert \mathbf{x}' - \mathbf{x} \vert^3}\right) d\mathbf{x}' = G \rho (\mathbf{x}) \int_{\vert \mathbf{x}' - \mathbf{x}\vert \leq h} \frac{\partial}{\partial \mathbf{x}'} \cdot \left( \frac{\mathbf{x}' - \mathbf{x}}{\vert \mathbf{x}' - \mathbf{x} \vert^3}\right) d \mathbf{x}' \tag{4}\]のように変形することができます。ここでガウスの定理を用いて、体積積分を表面での面積分にします。
\[\nabla^2 \Phi = G \rho (\mathbf{x}) \int_{\vert \mathbf{x}' - \mathbf{x}\vert = h} \frac{\mathbf{x}' - \mathbf{x}}{\vert \mathbf{x}' - \mathbf{x} \vert^3} \cdot d \mathbf{S}' \tag{5}\]さらに微小面積要素\(d\mathbf{S}'\)は、その微小面積要素を見込む微小立体角\(d\Omega\)を用いて
\[d\mathbf{S}' = (\mathbf{x}' - \mathbf{x}) h d\Omega \ \Longrightarrow \ \vert d \mathbf{S}'\vert = \underbrace{\vert \mathbf{x}'-\mathbf{x}\vert}_{=h} h d\Omega = h^2 d\Omega \equiv dS' \tag{6}\]のように変形することができます。
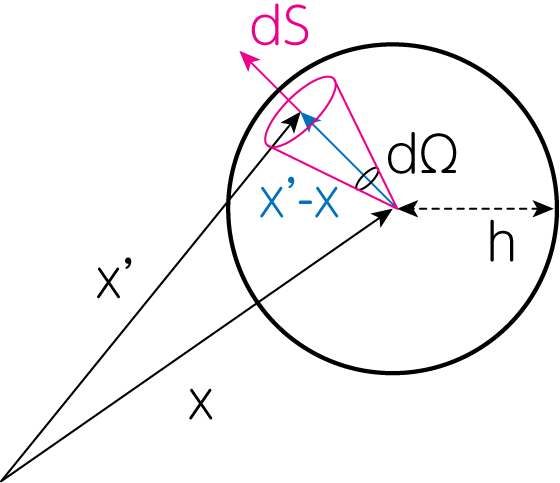
よって(5)式の面積分は立体角での積分に置き換えることができます。すると
\[\nabla^2 \Phi = G \rho (\mathbf{x}) \int_{4\pi} \frac{\mathbf{x}' - \mathbf{x}}{\vert \mathbf{x}' - \mathbf{x} \vert^3} \cdot (\mathbf{x}' - \mathbf{x}) h d\Omega = G \rho (\mathbf{x}) \int_{4\pi} d\Omega = 4\pi G \rho (\mathbf{x}) \tag{7}\]と求まります。これが導出したかったポアソン方程式です。
分布関数を用いた表現
ここまでは質量密度\(\rho (\mathbf{x})\)での表現でした。 実は分布関数\(f(\mathbf{x}, \mathbf{v})\)と\(\rho (\mathbf{x})\)との間には
\[\rho (\mathbf{x}) = m \int f(\mathbf{x}, \mathbf{v}) d\mathbf{x} \tag{8}\]のような関係があります。 \(f\)は位置\(\mathbf{x}\)にいる速度\(\mathbf{v}\)の粒子の数密度を表します。 よってこれを全速度で積分すれば、それは位置\(\mathbf{x}\)にいる粒子の数にとなります。 これを用いれば、ポアソン方程式は
\[\nabla^2 \Phi = 4\pi G m \int f (\mathbf{x}, \mathbf{v}) d \mathbf{v} \tag{9}\]のように書かれます。
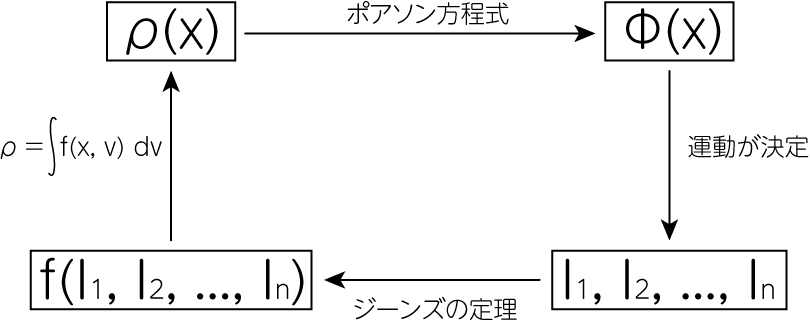
自己整合性 (self-consistency)
力学平衡にある重力多体系は、自己整合性を持つことで知られています。 例えば質量密度\(\rho(\mathbf{x})\)が与えられたとしましょう。 ポアソン方程式(7)から、重力ポテンシャル\(\Phi(\mathbf{x})\)が求まります。 この重力ポテンシャルから働く重力が求まり、その多体系での運動が決定されます。 すると運動の様子を記述する、運動の積分\(I_1, I_2, \dots, I_n\)が求まります。 ここまでくればジーンズの定理から、分布関数\(f(I_1, I_2, \dots, I_n)\)が求まります。 最後に分布関数を速度で積分することで、\(\rho\)が求められます。 こうして求めた\(\rho\)は最初に与えられた\(\rho\)と一致するはずです。このようにして、計算された結果に矛盾がないか(整合性が取れているか)を確かめることができます。