Table of contents
2.2.3 Eddington-Barbier relation
Source function が optical depth \(\tau_\nu\)の線形関数だと思って
\[S_\nu (\tau_\nu) = S_{0\nu} + S_{1\nu} \tau_\nu \tag{2.22}\]のように書くことができるとしましょう。ここで\(S_{0\nu}, S_{1\nu}\)は定数です。これを(2.21)式に代入して積分します。
\[\int_0^\infty e^{-\frac{t}{\mu}} \frac{dt}{\mu} = \int_0^\infty e^{-x} dx = 1\] \[\int_0^\infty t e^{-\frac{t}{\mu}} \frac{dt}{\mu} = \mu \int_0^\infty x e^{-x} dx = \mu \left( \left[-xe^{-x} \right]_0^\infty + \int_0^\infty e^{-x} dx \right) = \mu\]より
\[I_\nu^+ (0, \mu) = S_{0\nu} + S_{1\nu} \mu = S_\nu (\tau_\nu = \mu) \tag{2.23}\]が得られます。この式はEmergent Intensityが光の経路に沿ったoptical length \(\tau_\nu/\mu \sim 1\)の場所のSource functionとなっていることを表しています。またFlux \(F_\nu\)は
\[\begin{align} F_\nu &= \int_{4\pi} I_\nu^+ (0, \mu) \cos \theta d\Omega = 2\pi \int_0^1 I_\nu^+ (0, \mu) \mu d\mu = 2\pi \int_0^1 (S_{0\nu} + \mu S_{1\nu}) \mu d\mu \\ &= 2\pi \left( \frac{1}{2} S_{0\nu} + \frac{1}{3} S_{1\nu} \right) = \pi \left( S_{0\nu} + \frac{2}{3} S_{1\nu} \right) = \pi S_\nu(\tau_\nu = 2/3) \tag{2.24} \end{align}\]最初の\(\cos \theta\)は我々から見たときの面積の減少(有効面積)、そして積分の範囲が\(0\leq \mu \leq 1\)となっているのは\(-1 \leq \mu \leq 0\)で\(I_\nu^+ = 0\)(星の裏側が見えない効果)を表します。
この(2.23)式または(2.24)式をEddington-Barbier relation(またはEddington-Barbier approximation)と言います。この式は、吸収係数の小さい波長では大気の深部から光の表面に出てきていることを示しています。
続けて有効温度とLuminosityの関係を導出しましょう。\(L_\nu = 4\pi R^2 F_\nu (0)\)より
ここで\(F_\nu (0) \propto S_\nu (\tau_\nu = 2/3) \simeq B_\nu (\tau_\nu = 2/3)\)を用いました。これは光球面が\(\bar{\tau_\nu} \sim 2/3\)であり、これより内側は見えないことを意味しています。
2.2.4 Solar limb darkening

太陽のディスクは周縁部ほど暗く見えます。この現象は周縁減光(Limb darkening)と呼ばれます。Limb darkening は周縁に近いほど、\(\mu\)が小さい方向の光が我々に届いているために起こる現象で、\(I_\nu^+(0, \mu)/ I_\nu^+ (0,1)\)で表されます。\(\mu\)が小さい方向の光ほど、(2.23)式より表面に近いところのSource functionを反映しているため、周縁が暗くなります。
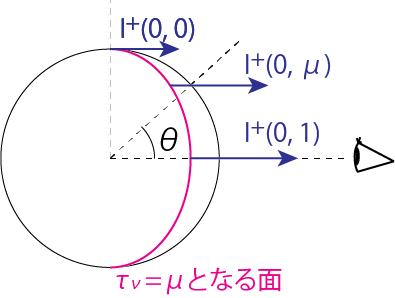
Eddington-Barbier approximationを用いると、(2.23)式より
\[\frac{I_\nu^+(0, \mu)}{I_\nu^+(0, 1)} = \frac{S_{0\nu} + S_{1\nu} \mu}{S_{0\nu} + S_{1\nu}} = a_\nu + b_\nu \mu \tag{2.25}\]のように表すことができます。したがって太陽のLimb darkeningを観測することによって、Source functionの深さに対する変化(LTEを仮定すると温度の変化)を知ることができます。