Table of contents
2.6 Gray Atmosphere (灰色大気)
ここでは、吸収係数・散乱係数が輻射の振動数に依存しない(平均値で置き換える)という簡単化を行って、恒星大気の性質を考察していきましょう。\(d\tau_\nu = -\rho (\kappa_\nu + \sigma_\nu) dr\)より、\(\tau_\nu \rightarrow \tau\)のように平均化します。この仮定とPlane parallelの仮定のもとでは、Radiative transferの式は
\[\mu \frac{dI_\nu}{d\tau} = I_\nu - S_\nu \tag{2.55}\]となります。この式を振動数に対して積分して
\[I \equiv \int_0^\infty I_\nu d\nu, \ J \equiv \int_0^\infty J_\nu d\nu, \ S \equiv \int_0^\infty S_\nu d\nu, \ B \equiv \int_0^\infty B_\nu d\nu, \ \rm{etc.}\]のように書くと
\[\mu \frac{dI}{d\tau} = I - S \tag{2.56}\]となります。さらにこの式を全立体角で積分すると
\[\frac{dF}{d\tau} = 4\pi (J-S) \tag{2.57}\]という関係が得られます。ここで\(F\)は(1.1)式で導出されたFlux \(F_\nu\)を振動数で積分した値で、全振動数領域で流れる輻射エネルギーフラックスを表します。Plane parallelかつ輻射のみでエネルギーが運ばれるとすると、大気中にエネルギー源がないのでFlux \(F\)は場所に依存せず一定でなければならない(\(\frac{dF}{d\tau} = 0\), 輻射平衡)ので
\[J = S \tag{2.58}\]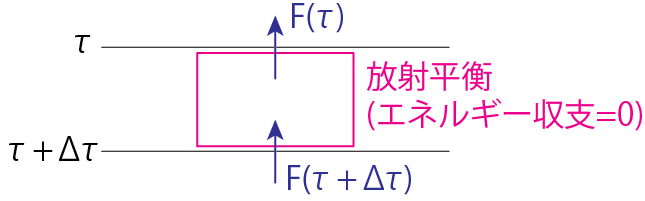
(2.58)式の関係を用いると、Radiative transferの式(2.56)は
\[\mu \frac{dI}{d\tau} = I - J \tag{2.59}\]となります。(2.59)式に\(\mu\)をかけて全立体角で積分すると、\(\int_{4\pi} \mu J d\Omega = J \int_{4\pi} \mu d\Omega = 0\)より
\[4\pi \frac{dK}{d\tau} = F \tag{2.60}\]が得られます。ここで\(K\)は(2.30)式で定義された\(K_\nu\)を全振動数で積分した量です。Flux \(F\)は\(\tau\)に関して一定なので、これは両辺を積分できて
\[K = \frac{1}{4\pi} F \tau + C \tag{2.61}\]が得られます。この関係を(2.59)に利用できるように、次のページでEddington近似を導入しましょう。
Appendix: Grayでないとき、放射平衡となる条件
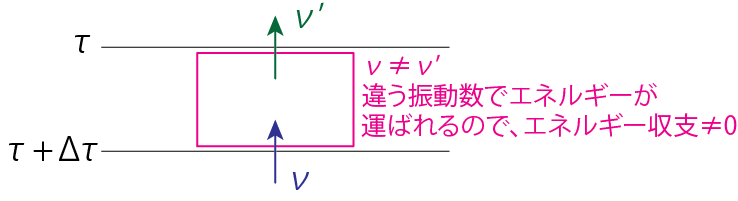
ここで\(S_\nu = \frac{\sigma_\nu J_\nu + \kappa_\nu B_\nu}{\kappa_\nu + \sigma_\nu}\)より
\[\int_0^\infty (\kappa_\nu + \sigma_\nu ) J_\nu d\nu = \int_0^\infty \sigma_\nu J_\nu d\nu + \int_0^\infty \kappa_\nu B_\nu d\nu \ \Longrightarrow \ \therefore \ \int_0^\infty \kappa_\nu B_\nu d\nu = \int_0^\infty \kappa_\nu J_\nu d\nu\]となります。