Table of contents

1. 大関法
   1. 概要
   2. 等式制約の表現
   3. 問題の変換
      1. Hubbard-Stratonovich変換
      2. 鞍点法
      3. Kullback-Leibler情報量とGibbsの自由エネルギーからの導出
   4. 最適化問題を解くためのアルゴリズム
   5. 数値実験
      1. K-minimum set of the random values
      2. Pythonスクリプト
      3. 数値実験結果
      4. \(\boldsymbol{\nu}\)の更新に用いる\(\eta\)について
2. 参考文献

大関法

概要

M. Ohzeki, 2020, “Breaking limitation of quantum annealer in solving optimization problems under constraints”を読んだので、その内容の理解を深めるために作成されたものです。

等式制約の表現

\(F_j(\mathbf{x}) = C_j \ (\forall j)\)のような等式制約がある最適化問題を数式で表現することを考えると、そのHamiltonianは

\[H_\mathrm{target} (\mathbf{x}) = H_0 (\mathbf{x}) + \sum_j \frac{\lambda_j}{2} (F_j (\mathbf{x}) - C_j)^2 \tag{1}\]

のように書かれます。ここで\(H_0\)は等式制約以外の項、そして第2項の\(\frac{1}{2}\)は後の変換を簡潔に表すための係数です。

問題の変換

Hubbard-Stratonovich変換

2乗の項を線形の形に変換する方法として、Hubbard-Stratonovich変換があります。これを適用するために\(H_\mathrm{target}\)が作るカノニカル分布の分布関数

\[Z = \sum_\mathbf{x} e^{-\beta H_\mathrm{target} (\mathbf{x})} \tag{2}\]

を用います。ここで\(\beta\)は逆温度(\(=1/T\))です。これにHubbard-Stratonovich変換を施します。

\[\begin{aligned} Z &= \sum_\mathbf{x} e^{-\beta H_0(\mathbf{x})} \exp \left\{ -\beta \sum_j \frac{\lambda_j}{2} (F_j (\mathbf{x}) - C_j)^2 \right\} \\ &= \sum_\mathbf{x} e^{-\beta H_0 (\mathbf{x})}\prod_j \exp \left\{ -\beta \frac{\lambda_j}{2} (F_j (\mathbf{x}) - C_j)^2 \right\} \\ &= \sum_\mathbf{x} e^{-\beta H_0 (\mathbf{x})}\prod_j \int_{-\infty}^\infty \frac{dz_j}{\sqrt{2\pi}} e^{-\frac{z_j^2}{2}} \exp \{ i z_j \sqrt{\beta \lambda_j} (F_j (\mathbf{x})-C_j)\} \end{aligned}\]

ここで\(z_j = -i \sqrt{\frac{\beta}{\lambda_j}} \nu_j\)と変数変換をすると

\[\begin{align} Z &\propto \sum_\mathbf{x} e^{-\beta H_0 (\mathbf{x})} \prod_j \int_{-\infty}^\infty d\nu_j \exp \left\{ \frac{\beta}{2\lambda_j} \nu_j^2+ \beta \nu_j (F_j (\mathbf{x})-C_j)\right\} \notag \\ &= \sum_\mathbf{x} e^{-\beta H_0 (\mathbf{x})} \left( \int_{-\infty}^\infty d\nu_0 \int_{-\infty}^\infty d\nu_1 \cdots \right) \exp \left\{ \frac{\beta}{2\lambda_0} \nu_0^2 + \beta \nu_0 (F_0 (\mathbf{x})-C_0)\right\} \exp \left\{ \frac{\beta}{2\lambda_1} \nu_1^2+ \beta \nu_1 (F_1 (\mathbf{x})-C_1)\right\}\cdots \notag \\ &= \sum_\mathbf{x} \prod_i \int_{-\infty}^\infty d\nu_i \exp \left\{ -\beta \left( - \sum_j\frac{\nu_j^2}{2\lambda_j} -\sum_j \nu_j (F_j (\mathbf{x})-C_j)+H_0 (\mathbf{x}) \right)\right\} \tag{3} \end{align}\]

となります。よって

\[H_\mathrm{eff} (\mathbf{x}, \boldsymbol{\nu}) \equiv - \sum_j\frac{\nu_j^2}{2\lambda_j} -\sum_j \nu_j (F_j (\mathbf{x})-C_j)+H_0 (\mathbf{x}) \tag{4}\]

のようにeffective Hamiltonianを用いて、この分布関数を表現することができます。

(1)式のままでは\(\lambda_j\)を適切にとる必要がありましたが、(4)式では\(\lambda_j \rightarrow \infty\)とすることができます。よって実際の実装では第2項・第3項のみを考えれば良いことがわかります。
後のためにさらにこれを変形しておきましょう。ボルツマン因子は

\[e^{-\beta H_\mathrm{eff}(\mathbf{x}, \boldsymbol{\nu})} = e^{\beta \sum_j \frac{\nu_j^2}{2\lambda_j}} e^{-\beta \sum_j \nu_j C_j} \exp \left\{ -\beta H_0 (\mathbf{x}) + \beta \sum_j \nu_j F_j (\mathbf{x}) \right\} \tag{5}\]

のように書き換えることができます。(3), (5)式より

\[Z \propto \prod_i \int_{-\infty}^\infty d\nu_i e^{\beta \sum_j \frac{\nu_j^2}{2\lambda_j}} e^{-\beta \sum_j \nu_j C_j} \sum_\mathbf{x} \exp \left\{ -\beta H_0 (\mathbf{x}) + \beta \sum_j \nu_j F_j (\mathbf{x}) \right\}\]

これから\(\boldsymbol{\nu}\)におけるeffective partition functionを

\[Z_\mathrm{eff}(\boldsymbol{\nu}) \equiv \sum_\mathbf{x} \exp \left\{ -\beta H_0 (\mathbf{x}) + \beta \sum_j \nu_j F_j (\mathbf{x}) \right\} \tag{6}\]

のように書くことができます。これを用いて分布関数は

\[\begin{aligned} Z &\propto \prod_i \int_{-\infty}^\infty d\nu_i e^{\beta \sum_j \frac{\nu_j^2}{2\lambda_j}} e^{-\beta \sum_j \nu_j C_j} e^{\log Z_\mathrm{eff}(\boldsymbol{\nu})} \\ &= \prod_i \int_{-\infty}^\infty d\nu_i \exp \left\{-\beta \left( - \sum_j \frac{\nu_j^2}{2\lambda_j} + \sum_j \nu_j C_j - \frac{1}{\beta} \log Z_\mathrm{eff}(\boldsymbol{\nu}) \right) \right\} \end{aligned}\]

と変形できます。ここから、\(\boldsymbol{\nu}\)におけるeffective Hamiltonianを

\[H_\mathrm{eff}(\boldsymbol{\nu}) \equiv - \sum_j \frac{\nu_j^2}{2\lambda_j} + \sum_j \nu_j C_j - \frac{1}{\beta} \log Z_\mathrm{eff}(\boldsymbol{\nu}) \tag{7}\]

のように定義することもできます。

鞍点法

(3)式において\(\beta \rightarrow \infty\)の極限をとると、\(\int d \nu_i\)の積分に寄与するのは\(H_\mathrm{eff} (\mathbf{x}, \boldsymbol{\nu})\)の最小値部分のみです。(4)式を変形してその最小値を計算しましょう。

\[H_\mathrm{eff} (\mathbf{x}, \boldsymbol{\nu}) = -\sum_j \frac{1}{2\lambda_j} (\nu_j + \lambda_j (F_j(\mathbf{x})-C_j))^2 + \sum_j \frac{\lambda_j}{2} (F_j(\mathbf{x})-C_j)^2 + H_0 (\mathbf{x})\]

第1項は必ずマイナスの値となるので、第2項が0となるような場所が最小値です。よって

\[F_j (\mathbf{x}) = C_j \quad (\forall j)\]

という等式制約が成り立ちます。ここから(4)式を最小化することは、(1)式の\(H_\mathrm{target}\)を最小化することに等しいことがわかります。

Kullback-Leibler情報量とGibbsの自由エネルギーからの導出

ここではHubbard-Stratonovich変換を用いない導出方法をご紹介します。分布\(P\)と分布\(Q\)におけるKullback-Leibler情報量(KL)は

\[\mathrm{KL}(P|Q) = \sum_\mathbf{x} Q(\mathbf{x}) \log \left( \frac{Q(\mathbf{x})}{P(\mathbf{x})}\right)\]

です。ここで分布\(P\)は

\[P(\mathbf{x}) = \frac{1}{Z} e^{-\beta H_0 (\mathbf{x})}\]

のように\(F_j(\mathbf{x})=C_j\)の制約がない場合のHamiltonianによるボルツマン分布とします。そして分布\(Q\)は\(F_j(\mathbf{x}) =C_j\)の制約を満たし、KLが最小となるような分布です。この条件から、Gibbsの自由エネルギーが

\[G(\mathbf{C}) = \min_Q \left( E-\frac{S}{\beta} \right)\]

のように求まります。ここで\(E = \sum_\mathbf{x} Q(\mathbf{x}) H_0(\mathbf{x})\)はエネルギー、そして\(S= -\sum_\mathbf{x} Q(\mathbf{x}) \log Q(\mathbf{x})\)はエントロピーです。

KLからGを導くことができない...どなたか証明の詳細をご教示いただけると助かりますm(-_-)m

\(Q\)の形として、ラグランジュ未定乗数と(6)式の\(Z_\mathrm{eff}\)を用いて

\[Q (\mathbf{x}) = \frac{1}{Z_\mathrm{eff}} \exp \left\{ -\beta \left(H_0 (\mathbf{x}) - \sum_j \nu_j F_j(\mathbf{x})\right)\right\}\]

としましょう。この\(Q\)の形の中で\(\boldsymbol{\nu}\)をどのように選べば\(G(\mathbf{C})\)を最小にできるかを考えます。

\[\begin{aligned} G(\mathbf{C}) &= \min_Q \left[ \sum_\mathbf{x} Q (\mathbf{x})\left( H_0 (\mathbf{x}) + \frac{1}{\beta} \log Q(\mathbf{x})\right) \right] \\ &= \min_Q \left[ \sum_\mathbf{x} Q (\mathbf{x})\left( H_0 (\mathbf{x}) + \frac{1}{\beta} \log \frac{1}{Z_\mathrm{eff}} -H_0 (\mathbf{x}) + \sum_j \nu_j F_j(\mathbf{x})\right) \right] \\ &= \min_Q \left[ \sum_\mathbf{x} Q(\mathbf{x}) \left(\sum_j \nu_j F_j (\mathbf{x})-\frac{1}{\beta} \log Z_\mathrm{eff} \right)\right] \end{aligned}\]

\(F_j=C_j\)の制約を満たすことと合わせて

\[G(\mathbf{C}) = \min_{\boldsymbol{\nu}} \left[ \sum_j \nu_j C_j - \frac{1}{\beta} \log Z_\mathrm{eff}\right]\]

これは(7)式を最小化することを意味しています。このことから、このようにKLとGibbs自由エネルギーを用いた導出も同じ結果となることができます。

最適化問題を解くためのアルゴリズム

以下に、この手法を用いて最適化問題を解くアルゴリズムを示します。

• step 1: 初期未定乗数\(\boldsymbol{\nu}^{t=0}\)を決定します。
• step 2: (量子)アニーリングなどを用いて、この変換で2乗の項を線形にしたハミルトニアンを最小化します。
• step 3: 制約が満たされた\((F_j(\mathbf{x})=C_j \ \forall j)\)ならば、終了します。
• step 4: \(\nu_j^{t+1} = \nu_j^t + \eta (C_j - F_j(\mathbf{x}))\)として、次の反復での\(\boldsymbol{\nu}^{t+1}\)を計算します。\(t \leftarrow t+1\)として、step 2に戻ります。

数値実験

K-minimum set of the random values

今回の数値実験はK-minimum set問題です。いくつかの乱数の中から\(K\)個だけ選び出し、その数の総和が最小になる組み合わせを探索します。このとき、普通の実装では

\[H_\mathrm{target}(\mathbf{x}) = \sum_{i=0}^{N-1} h_i x_i + \frac{\lambda}{2} \left(\sum_{i=0}^{N-1} x_i -K\right)^2\]

となります。ここで\(N\)は\([0, 1]\)の範囲の乱数の総数、\(h_i \ (i = 0, \dots, N-1)\)は乱数列、\(x_i\)は\(i\)番目の乱数を選ぶとき1, そうでないとき0となるバイナリ変数です。
これを(4)式のeffective Hamiltonianに当てはめると

\[H_\mathrm{eff}(\mathbf{x}, \nu) = -\nu \left( \sum_{i=0}^{N-1} x_i -K\right) + \sum_{i=0}^{N-1} h_i x_i\]

となります。これを実装します。

Pythonスクリプト

以下に、今回実装したPythonスクリプトをアップロードしました。

Link button

数値実験結果

num_reads=1, \(\eta=0.0001\)、そして乱数の総数\(N=2000\)でアニーリングを行った結果を以下に示します。これは横軸に未定乗数更新step数、縦軸には最適解における目的関数からの値のズレの大きさを描画しています。

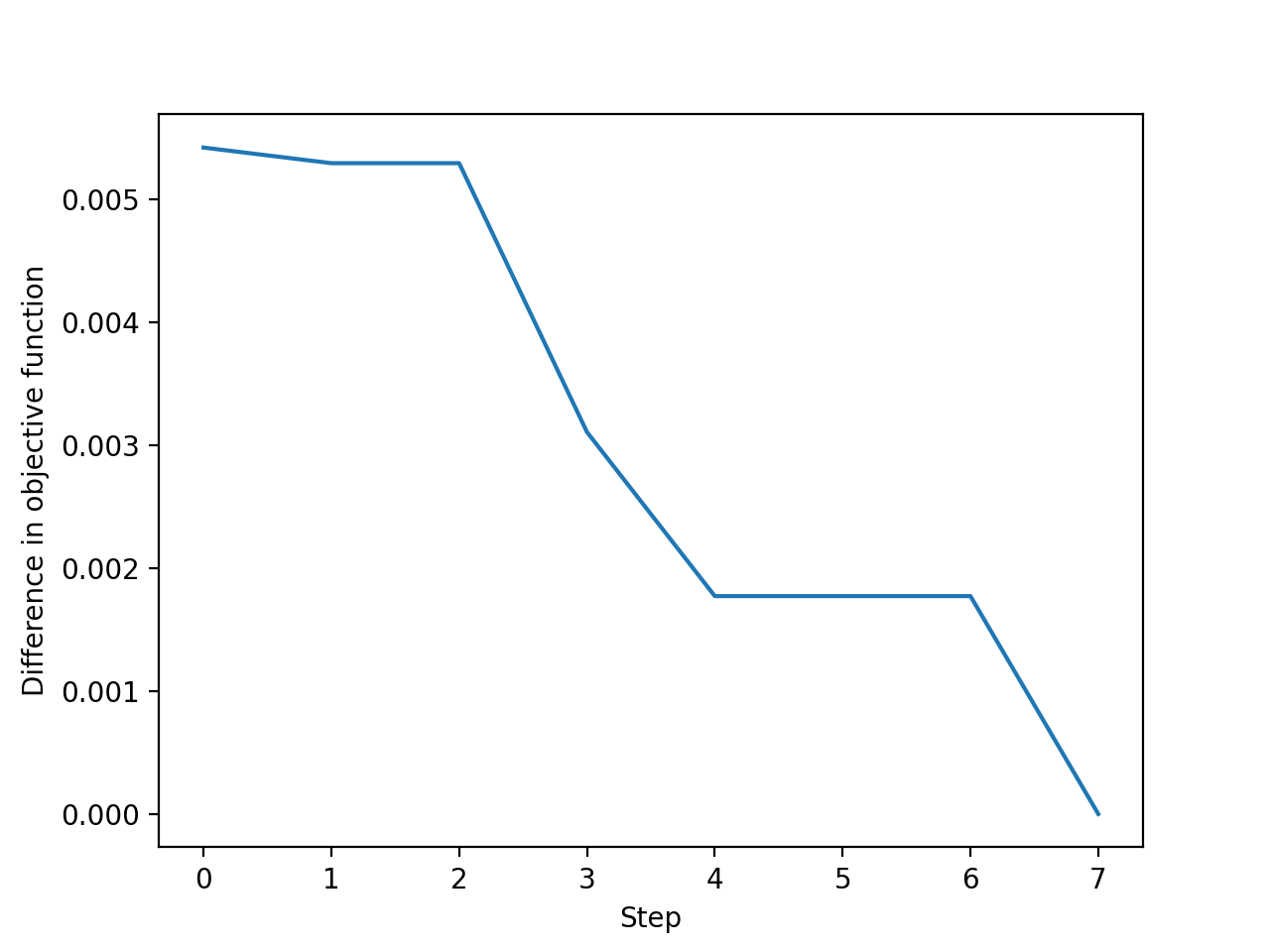
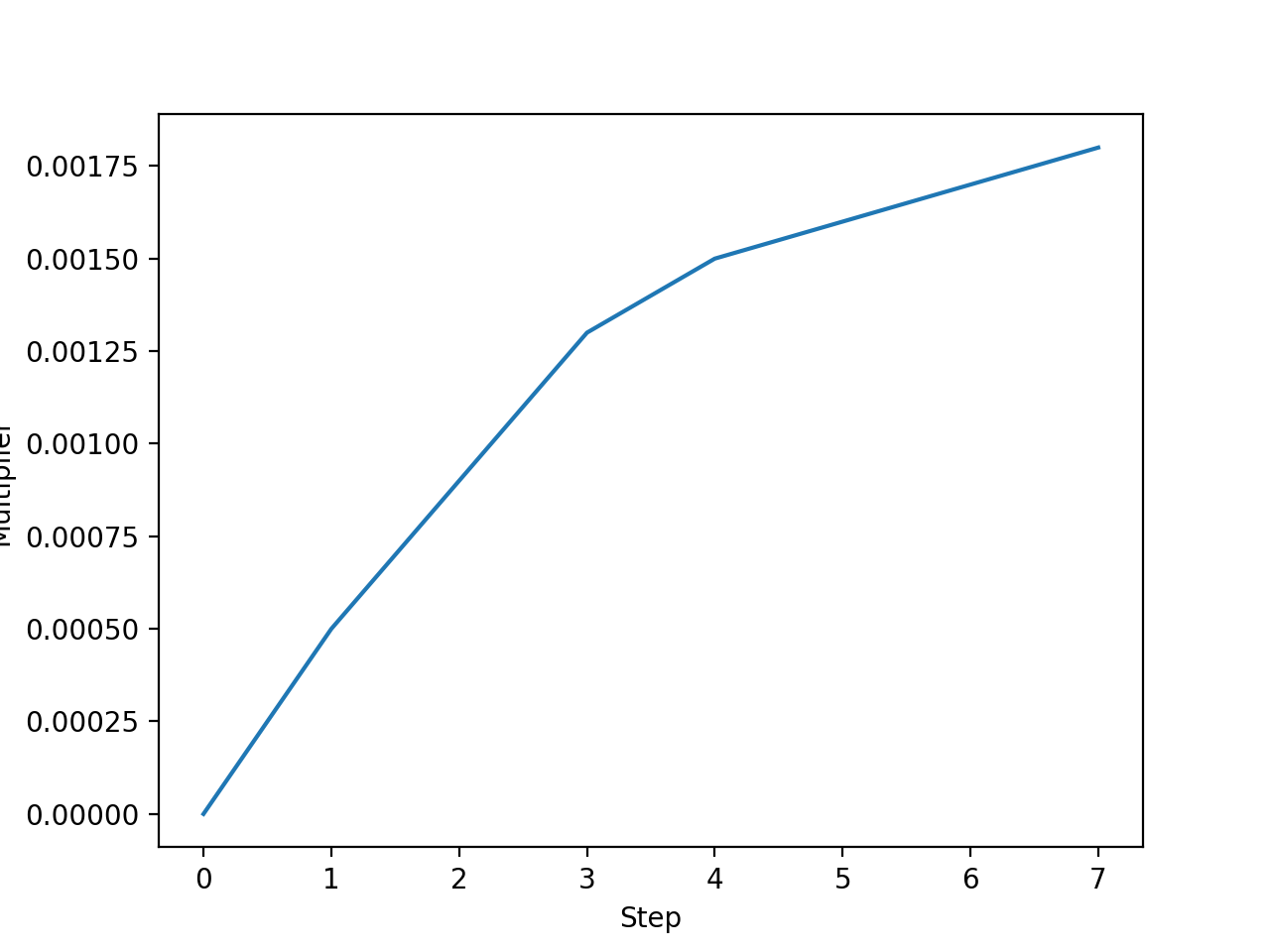
数回実行したところ、5~20step程度で最適解を発見できていました。さらに以下の図は横軸に未定乗数更新step数、縦軸に未定乗数\(\nu\)の値を描画したものです。

\(\boldsymbol{\nu}\)の更新に用いる\(\eta\)について

\(\eta\)の値を適切に取らないと、最適解周辺で振動するような振る舞いが見られます。以下は\(\eta=0.001\)の場合の最適解における目的関数からの値のズレの大きさを描画したものです。

この問題の場合、\(\eta=1/N\)程度がちょうど良いようです。

参考文献

• M. Ohzeki, 2020, “Breaking limitation of quantum annealer in solving optimization problems under constraints”
• 情報統計物理学 ランダムスピン系