Table of contents
Energy Equipartition
ここでは物質密度が等しくなる時期を計算し、どの時期でどの物質が優勢かを調べてみましょう。
相対論的物質と普通の物質
\[\rho_r (z_{\rm eq})/ \rho_m (z_{\rm eq}) = 1\]となる時を\(z_{\rm eq}\)としましょう。エネルギー保存より
\[\rho_m = \rho_{m, 0} (1+z)^3 = \Omega_{m, 0} \rho_{\rm cr, 0} (1+z)^3\]ここで\(\Omega_{m, 0} = \rho_{m, 0} / \rho_{\rm cr, 0}\), \(\rho_{\rm cr, 0} \simeq 2 \times 10^{-29} h^2\), そして\(h = H_0/100{\rm km/s/Mpc}\)です。
\[\rho_r = (\Omega_{\gamma, 0} + \Omega_{\nu, 0}) \rho_{\rm cr, 0} (1+z)^4 \simeq 4.15 \times 10^{-5} h^{2} \rho_{\rm cr, 0} (1+z)^4\] \[\therefore \ \frac{\rho_r}{\rho_m} = \frac{4.15 \times 10^{-5}}{\Omega_{m, 0} h^2} (1+z) = 1 \ \Longrightarrow \ 1 + z_{\rm eq} = 2.4 \times 10^4 \Omega_{m, 0} h^2\]です。\(z_{\rm eq} \sim 10^3\)程度なので、現在\(z=0\)は物質が優勢ということになります。
普通の物質とダークエネルギー
ダークエネルギーが\(\Lambda\)項で表現されると仮定すると\(w_\mathrm{DE} = w_{\Lambda} = -1\)より、エネルギー保存から
\[\rho_\Lambda = \rho_{\Lambda, 0} = \Omega_{\Lambda, 0} \rho_{\rm cr, 0}\]です。ここで観測の結果から\(\Omega_{\Lambda, 0} = 1-\Omega_{m, 0} \sim 0.73\)とすると
\[\rho_{\Lambda} / \rho_m (z_{\rm eq}) = 1\]となる時期は
\[\frac{\Omega_{\Lambda, 0}}{\Omega_{m, 0} h^2 (1+z_{\rm eq})^3} = 1 \ \Longrightarrow \ 1+ z_{\rm eq} = \left(\frac{1-\Omega_{m, 0}}{\Omega_{m, 0}} \right)^{1/3} h^{-2/3} \sim 1.82 \ \Longrightarrow \ \therefore \ z_{\rm eq} \sim 0.82\]です。現在\(z=0\)はダークエネルギーが優勢ということになります。図示すると以下のようになります。
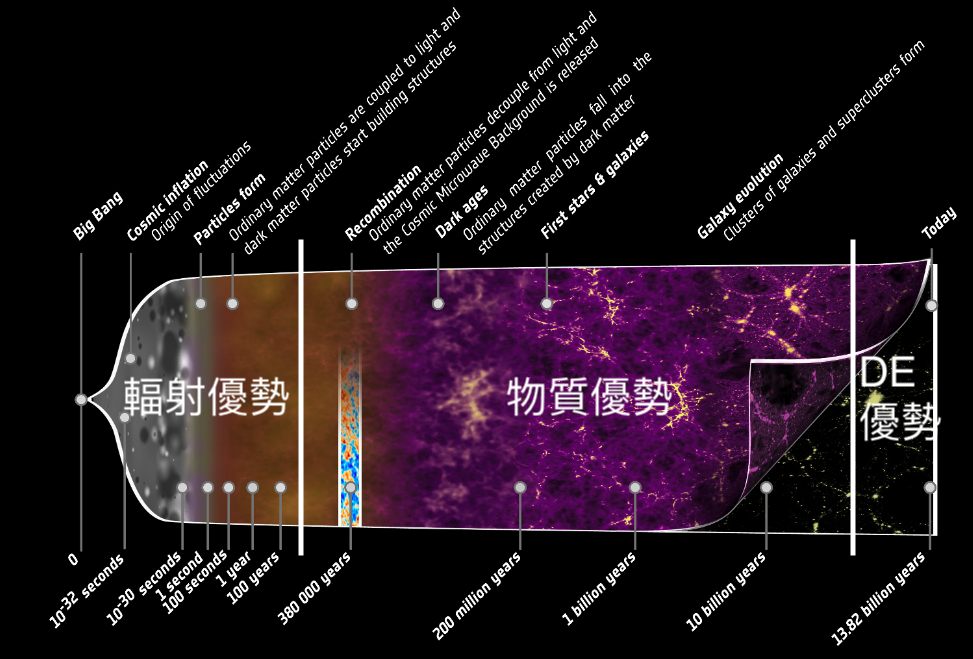
宇宙初期には輻射(相対論的な物質)が優勢です。その後、物質優勢な宇宙に進化し、最後にダークエネルギー優勢な宇宙へと変化してきたというモデルです。