Table of contents
ストークスパラメータ
\(z\)方向に伝搬する単色電磁波の電場の各成分が
\[\begin{align} E_x &= a_1 \cos (\tau + \delta_1) \notag \\ E_y &= a_2 \cos (\tau + \delta_2) \notag = a_2 \cos (\tau + \delta_1 + \delta) \end{align} \tag{1}\]で表されるとします。 ここで\(\delta=\delta_2- \delta_1\)、さらに\(\tau \equiv \omega t - k_z z\)などのように書きました。 偏光の状態は通常、ストークスパラメータ(Stokes parameters)と呼ばれる以下の式で定義される4つの物理量で表されます。
\[I = a_1^2 + a_2^2 \tag{2}\] \[Q = a_1^2 - a_2^2 \tag{3}\] \[U = 2 a_1 a_2 \cos \delta \tag{4}\] \[V = 2 a_1 a_2 \sin \delta \tag{5}\]ストークスパラメータの間に成り立つ公式その1
\[\begin{align} Q^2 + U^2 + V^2 &= a_1^4 -2 a_1^2 a_2^2 + a_2^4 + 4 a_1^2 a_2^2 \cos^2 \delta + 4 a_1^2 a_2^2 \sin^2 \delta = a_1^4 + 2 a_1^2 a_2^2 + a_2^4 \notag \\ &= (a_1^2 + a_2^2)^2 = I^2 \tag{6} \end{align}\]が成り立つことから、実は独立はストークスパラメータは3つです。これは偏光状態を特徴つける物理量が\(a_1, a_2, \delta\)の3つだったことに対応しています。
ストークスパラメータと偏光の対応
以下の4つの場合について電磁波の電場成分の振動方向を\(xy\)平面内に描いてみましょう。
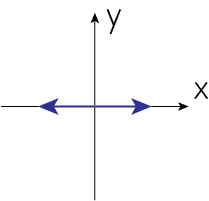
\(\delta=0, Q>0, U=0\)
\(\delta=0\)より
\[U = 2 a_1 a_2 = 0 \ \Longrightarrow \ a_1 = 0 \ \mathrm{or} \ a_2 = 0\]さらに\(Q = a_1^2 - a_2^2 > 0\)より\(a_2 = 0\)です。よって電場を図示すると以下のようになります。
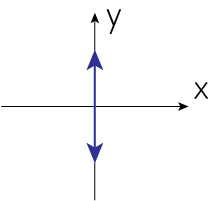
\(\delta=0, Q<0, U=0\)
\(\delta=0\)より
\[U = 2 a_1 a_2 = 0 \ \Longrightarrow \ a_1 = 0 \ \mathrm{or} \ a_2 = 0\]さらに\(Q = a_1^2 - a_2^2 < 0\)より\(a_1 = 0\)です。よって電場を図示すると以下のようになります。
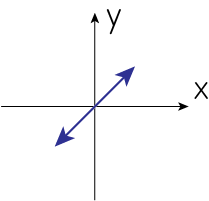
\(\delta=0, Q=0, U>0\)
\(Q=0\)より
\[Q = a_1^2 - a_2^2 = 0 \ \Longrightarrow \ a_1 = \pm a_2\]さらに\(\delta=0\)より\(U = 2 a_1 a_2 > 0\)です。よって電場を図示すると以下のようになります。
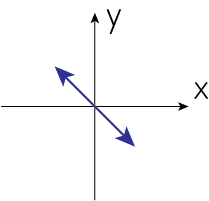
\(\delta=0, Q=0, U<0\)
\(Q=0\)より
\[Q = a_1^2 - a_2^2 = 0 \ \Longrightarrow \ a_1 = \pm a_2\]さらに\(\delta=0\)より\(U = 2 a_1 a_2 < 0\)です。よって電場を図示すると以下のようになります。
ストークスパラメータの意味
以上の4つの対応から、直線偏光のときは\(V=0\)であり、\(V\)は円偏光を特徴付ける量です。一方、円偏光の時は\(Q=U=0\)であることから、これら2つは直線偏光を特徴付ける量と言えます。\(I\)は強度と等価な量ですが、正確には平均強度の2倍の量です。
完全・部分・無偏光と偏光度
(5)式が成り立つとき、その電磁波は完全偏光している、といいます。しかし、現実の電磁波は全てが完全偏光している訳ではありません。例えば、多くの自然光は無偏光です。以下では無偏光電磁波がどのように実現しているのかを考察してみましょう。
多くの場合、現実の電磁波は継続時間が有限のパルス波の重ね合わせで実現されています。このパルス波を波連と呼びます。1つの波連がある特定の偏光状態にあるとしましょう。無偏光電磁波はこの波連の初期位相と発せられる時刻および偏光状態がランダムであるときに実現します。波連の継続時間より十分長い観測時間で偏光板を使って観測する状況を考えましょう。特別な方向が存在しないので、偏光板をどの方向に傾けても得られる強度は一定となるはずです。したがって、直線偏光していないという測定結果を得ます。同様に円偏光を測定しても、右回りと左回りがほぼ同数存在するため、円偏光していないという結果になります。
波連の一部があるときは円偏光、またあるときは直線偏光、それらが重ね合わさることで無偏光状態となります。上述の議論から、無偏光状態では
となります。
一方、現実の電磁波で完全偏光した状態とは、全ての波連が同じ偏光状態である場合です。
一般的には、完全偏光した状態と無偏光状態の重ね合わせです。したがって、ストークスパラメータは
という関係を満たします。そこで電磁波の偏光の度合いを表す物理量として偏光度\(\Pi\)を以下のように定義します。
\[\Pi \equiv \frac{\sqrt{Q^2 + U^2 + V^2}}{I} \tag{7}\]偏光度が0のときは無偏光、1のときは完全偏光、そして\(0<\Pi<1\)の時は部分偏光となります。
電磁波とストークスパラメータの複素数表現
電磁波を三角関数で表記すると計算が煩雑になるため、電磁波を以下のように複素数表記し、実際に観測される電場としてはその実部を取ることにします。 すると(1)式は
\[\mathcal{E}_x = a_1 e^{i(\tau + \delta_1)}, \quad \mathcal{E}_y = a_2 e^{i(\tau + \delta_2)} = a_2 e^{i(\tau + \delta_1 + \delta)} \tag{8}\]のように書かれます。 これらを用いると、\(a_1^2 = \mathcal{E}_x \mathcal{E}_x^\ast, a_2^2 = \mathcal{E}_y \mathcal{E}_y^\ast, e^{-i\delta} = \mathcal{E}_x \mathcal{E}_y^\ast\)などより、(2)~(5)式は
\[I = \mathcal{E}_x \mathcal{E}_x^\ast + \mathcal{E}_y \mathcal{E}_y^\ast \tag{9}\] \[Q = \mathcal{E}_x \mathcal{E}_x^\ast - \mathcal{E}_y \mathcal{E}_y^\ast \tag{10}\] \[U = 2 \mathrm{Re} (\mathcal{E}_x \mathcal{E}_y^\ast) = \mathcal{E}_{x} \mathcal{E}_{y}^\ast + \mathcal{E}_{x}^\ast \mathcal{E}_{y} \tag{11}\] \[V = - 2 \mathrm{Im} (\mathcal{E}_x \mathcal{E}_y^\ast) = - (\mathcal{E}_{x} \mathcal{E}_{y}^\ast - \mathcal{E}_{x}^\ast \mathcal{E}_{y}) \tag{12}\]のように書き換えることができます。
ストークスパラメータの回転座標変換
もう一つ、偏光方向についての式も導出してみましょう。 \(x, y\)座標系においてストークスパラメータ\(I, Q, U, V\)を持つ偏光電磁波を考えます。 それとは別に角度\(\theta\)だけ回転された座標系\(x', y'\)で、この偏光電磁波を観測することを考えましょう。 これは私たち観測者は飛来する電磁波の偏光方向を事前に知ることはできないため、電磁波を放射した粒子系で偏光を考えた座標と、設置した観測装置の検出座標の違いを表しています。
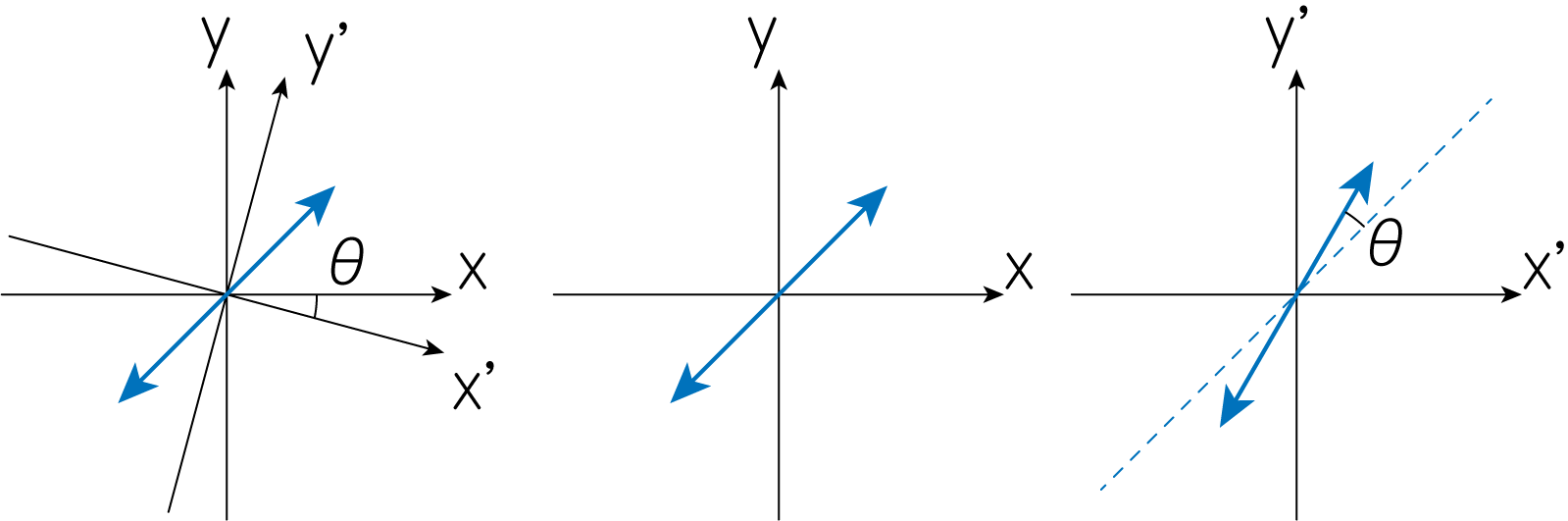
すると\(x', y'\)方向の電場成分は、回転行列を用いて
\[\left( \begin{array}{c} \mathcal{E}_{x'} \\ \mathcal{E}_{y'} \end{array} \right) = \left( \begin{array}{cc} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array}\right) \left( \begin{array}{c} \mathcal{E}_{x} \\ \mathcal{E}_{y} \end{array} \right) \tag{13}\]のように書かれます。 この\(x', y'\)座標系のストークスパラメータ\(I', Q', U', V'\)を求めてみましょう。
\[\begin{align} I' &= \mathcal{E}_{x'} \mathcal{E}_{x'}^\ast + \mathcal{E}_{y'} \mathcal{E}_{y'}^\ast \notag \\ &= \mathcal{E}_{x} \mathcal{E}_{x}^\ast \cos^2 \theta - (\mathcal{E}_{x} \mathcal{E}_{y}^\ast + \mathcal{E}_{y} \mathcal{E}_{x}^\ast) \cos \theta \sin \theta + \mathcal{E}_{y} \mathcal{E}_{y}^\ast \sin^2 \theta \notag \\ & \qquad + \mathcal{E}_{x} \mathcal{E}_{x}^\ast \sin^2 \theta + (\mathcal{E}_{x} \mathcal{E}_{y}^\ast + \mathcal{E}_{y} \mathcal{E}_{x}^\ast) \sin \theta \cos \theta + \mathcal{E}_{y} \mathcal{E}_{y}^\ast \cos^2 \theta \notag \\ &= \mathcal{E}_{x} \mathcal{E}_{x}^\ast + \mathcal{E}_{y} \mathcal{E}_{y}^\ast = I \tag{14} \end{align}\] \[\begin{align} Q' &= \mathcal{E}_{x'} \mathcal{E}_{x'}^\ast - \mathcal{E}_{y'} \mathcal{E}_{y'}^\ast \notag \\ &= \mathcal{E}_{x} \mathcal{E}_{x}^\ast \cos^2 \theta - (\mathcal{E}_{x} \mathcal{E}_{y}^\ast + \mathcal{E}_{y} \mathcal{E}_{x}^\ast) \cos \theta \sin \theta + \mathcal{E}_{y} \mathcal{E}_{y}^\ast \sin^2 \theta \notag \\ & \qquad - \mathcal{E}_{x} \mathcal{E}_{x}^\ast \sin^2 \theta - (\mathcal{E}_{x} \mathcal{E}_{y}^\ast + \mathcal{E}_{y} \mathcal{E}_{x}^\ast) \sin \theta \cos \theta - \mathcal{E}_{y} \mathcal{E}_{y}^\ast \cos^2 \theta \notag \\ &= (\mathcal{E}_{x} \mathcal{E}_{x}^\ast - \mathcal{E}_{y} \mathcal{E}_{y}^\ast) (\cos^2 \theta - \sin^2 \theta) - 2 (\mathcal{E}_{x} \mathcal{E}_{y}^\ast + \mathcal{E}_{y} \mathcal{E}_{x}^\ast) \cos \theta \sin \theta = Q \cos 2\theta - U \sin 2\theta \tag{15} \end{align}\] \[\begin{align} U' &= \mathcal{E}_{x'} \mathcal{E}_{y'}^\ast + \mathcal{E}_{x'}^\ast \mathcal{E}_{y'} \notag \\ &= \mathcal{E}_{x} \mathcal{E}_{x}^\ast \sin \theta \cos \theta + \mathcal{E}_{x} \mathcal{E}_{y}^\ast \cos^2 \theta - \mathcal{E}_{x}^\ast \mathcal{E}_{y} \sin^2 \theta - \mathcal{E}_{y} \mathcal{E}_{y}^\ast \sin \theta \cos \theta \notag \\ & \qquad + \mathcal{E}_{x}^\ast \mathcal{E}_{y} \cos \theta \sin \theta + \mathcal{E}_{x}^\ast \mathcal{E}_{y} \cos^2 \theta - \mathcal{E}_{y}^\ast \mathcal{E}_{x} \sin^2 \theta - \mathcal{E}_{y}^\ast \mathcal{E}_{x} \sin \theta \cos \theta \notag \\ &= (\mathcal{E}_{x} \mathcal{E}_{x}^\ast - \mathcal{E}_{y} \mathcal{E}_{y}^\ast) \sin 2\theta + (\mathcal{E}_{x} \mathcal{E}_{y}^\ast + \mathcal{E}_{x}^\ast \mathcal{E}_{y}) \cos 2\theta = Q \sin 2\theta + U \cos 2\theta \tag{16} \end{align}\] \[\begin{align} V' &= - (\mathcal{E}_{x'} \mathcal{E}_{y'}^\ast - \mathcal{E}_{x'}^\ast \mathcal{E}_{y'}) \notag \\ &= - \mathcal{E}_{x} \mathcal{E}_{x}^\ast \sin \theta \cos \theta - \mathcal{E}_{x} \mathcal{E}_{y}^\ast \cos^2 \theta + \mathcal{E}_{y} \mathcal{E}_{x}^\ast \sin^2 \theta + \mathcal{E}_{y} \mathcal{E}_{y}^\ast \sin \theta \cos \theta \notag \\ & \qquad + \mathcal{E}_{x}^\ast \mathcal{E}_{x} \cos \theta \sin \theta + \mathcal{E}_{x}^\ast \mathcal{E}_{y} \cos^2 \theta - \mathcal{E}_{x} \mathcal{E}_{y}^\ast \sin^2 \theta - \mathcal{E}_{y} \mathcal{E}_{y}^\ast \sin \theta \cos \theta \notag \\ &= - \mathcal{E}_{x} \mathcal{E}_{y}^\ast + \mathcal{E}_{y} \mathcal{E}_{x}^\ast = V \tag{17} \end{align}\]これらをまとめると、以下の一つの式にまとめることができます。
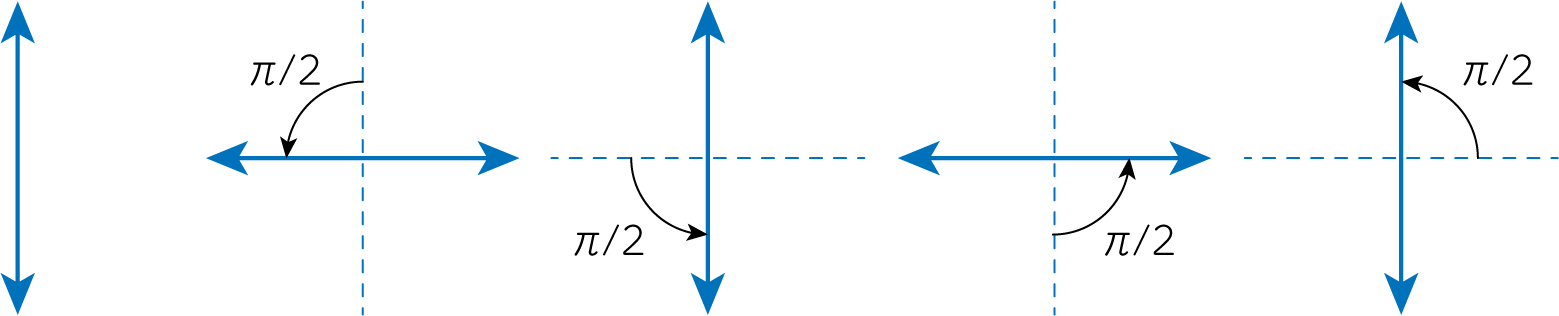
\[\left( \begin{array}{c} I \\ Q \\ U \\ V \end{array} \right) = \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & \cos 2\theta & -\sin 2\theta & 0 \\ 0 & \sin 2\theta & \cos 2\theta & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) \left( \begin{array}{c} I' \\ Q' \\ U' \\ V' \end{array} \right) \tag{18}\]\(I\)は電磁波の振幅に対応するものであるため、回転変換に対しては不変です。 また\(V\)は円偏光に関連するパラメータであるため、これも変化はありません。 よって直線偏光に関するパラメータである\(Q, V\)だけが影響を受けることがわかります。 \(\theta\)の回転座標変換に対して\(2\theta\)の角度が現れるのは、電磁波がスピン2であることに対応します(下図のように、直線偏光の矢印が2\(\pi\)の回転の間に2回もとに戻ることからわかります。)
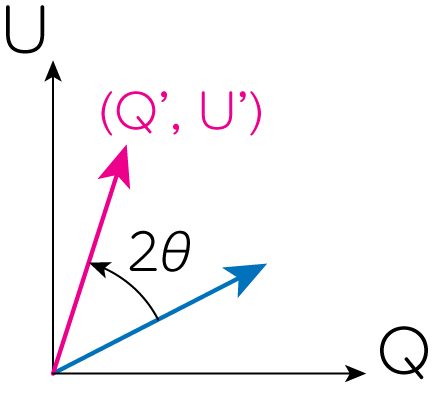
(18)式から、\(Q, U\)の部分だけを取り出しましょう。
\[\left( \begin{array}{c} Q' \\ U' \end{array} \right) = \left( \begin{array}{cc} \cos 2\theta & -\sin 2\theta \\ \sin 2\theta & \cos 2\theta \end{array} \right) \left( \begin{array}{c} Q \\ U \end{array} \right) \tag{19}\]この変換から、実空間上で直線偏光の向きを\(\theta\)回転させる変換は、\(Q, U\)平面上で\(2\theta\)回転させることに対応します。 そして回転であることから、\(Q^2 + U^2\) (下図のベクトルの長さの2乗)は変化しないことがわかります。
偏光角の計算
元々のストークスパラメータ\(Q, U\)の値により表現される直線偏光の角度が\(\chi\)であったとしましょう。 ここまでの議論から、実空間上での偏光角\(\chi\)は、\(Q, U\)平面では\(2\chi\)の角度を持つことに対応します。 よって
\[\tan 2\chi = \frac{U}{Q} \ \Longrightarrow \ \chi = \frac{1}{2} \tan^{-1} \frac{U}{Q} \tag{20}\]と求まります。 これは検出器を用意し、ストークスパラメータ\(Q, U\)を測定すれば、偏光角\(\chi\)を推定することができることを表す式です。
複素偏光強度
ここまでの議論から
\[U = \sqrt{Q^2 + U^2} \cos 2\chi, \quad Q = \sqrt{Q^2 + U^2} \sin 2\chi \tag{21}\]のように書くことができます。 もし観測している電磁波に円偏光成分がなく\(V = 0\)で、さらに偏光度が1であるならば、(7)式より
\[\Pi = \frac{\sqrt{Q^2 + U^2}}{I} = 1 \ \Longrightarrow \ \sqrt{Q^2 + U^2} = I \tag{22}\]となることから、(21)式は
\[U = I \cos 2\chi, \quad Q = I \sin 2\chi \tag{23}\]と表記できます。 さらに便利にするために、この直線偏光を以下のような複素数で特徴づけることにしましょう。
\[P \equiv I e^{i 2\chi} = U + i Q \tag{24}\]これを複素偏光強度と呼びます。 このようにしておくことで、直線偏光に関する計算の取り扱いが楽になります。
参考文献
[1] 観山正見, 二間瀬敏史, 野本憲一, ”天体物理学の基礎 II”
[2] 松原隆彦, ”現代宇宙論 -時空と物質の共進化”
[3] 中村文隆, 鶴剛, 長田哲也, 藤沢健太, 梅村雅之, 福江純, “放射素過程の基礎”