Table of contents
Thomson散乱
自由電子による電磁波の散乱を考えましょう。直線偏光した単色電磁波
\[\mathbf{E} = (E_0 \cos \omega_0 t) \boldsymbol{\epsilon}\]が自由電子(質量\(m_e\), 電荷\(-e\))に入射することで、電子を振動させます。ここで\(\boldsymbol{\epsilon}\)は輻射場の電場の方向を表す時間・空間に依存しない単位ベクトルで、これを偏光ベクトルと呼びます。以下ではその自由電子によって放出された電磁波(2次波)を、電子による散乱波と考えて散乱断面積を導出しましょう。ただし、ここでは電子の運動は非相対論的であるとします。
非相対論的な輻射場の放射強度
電子の運動方程式は、電場の式より
\[m_e \ddot{\mathbf{r}} = - e (E_0 \cos \omega_0 t ) \boldsymbol{\epsilon} \tag{1}\]電磁波を放出する電子の運動が非相対論的であるときの輻射場はLinard-Wiechertポテンシャルからの電磁場導出で導いた公式より
\[\mathbf{E} = - \frac{e}{c} \frac{\mathbf{n} \times (\mathbf{n} \times \dot{\boldsymbol{\beta}})}{\kappa^3 R} \tag{2}\]ここで電子の運動が非相対論的であることから、遅延時間量を普通の時刻のものに置き換えました。分子部分を計算すると
\[\mathbf{n} \times (\mathbf{n}\times \dot{\boldsymbol{\beta}}) = (\mathbf{n} \cdot \dot{\boldsymbol{\beta}}) \mathbf{n} - (\mathbf{n}\cdot \mathbf{n}) \dot{\boldsymbol{\beta}} = \dot{\beta}\cos \Theta \mathbf{n} -\dot{\boldsymbol{\beta}}\]ここで観測者の方向ベクトル\(\mathbf{n}\)と電子の加速度ベクトル\(\dot{\boldsymbol{\beta}}\)との成す角を\(\Theta\)としました。これよりこのベクトルの大きさは
\[|\mathbf{n} \times (\mathbf{n}\times \dot{\boldsymbol{\beta}})|^2 = \dot{\beta}^2 \cos^2 \Theta -2 \dot{\beta}^2 \cos^2 \Theta + \dot{\beta}^2 = \dot{\beta}^2 \sin^2 \Theta\]です。よって求めたい放射強度(emitted power)は
\[\frac{dP}{d\Omega} = \frac{c}{4\pi} R^2 \frac{e^2}{c^2} \frac{\dot{\beta}^2\sin^2 \Theta}{R^2} = \frac{e^2}{4\pi c^3} \ddot{r}^2 \sin^2 \Theta\](1)式より
\[\frac{dP}{d\Omega} = \frac{1}{4\pi c^3} \left( \frac{e^2 E_0}{m_e}\right)^2 \sin^2 \Theta \cos^2 \omega_0 t \tag{2}\]ここで(2)式の時間平均を考えましょう。時間平均とは電磁波の一周期\(T\)にわたる平均と考えても、周期より十分長い時間\(T\)にわたる平均(長時間平均)と考えても差し支えありません。長時間平均は実際の観測で行われる操作と近いため、ここでは後者として取り扱います。すると
\[\begin{align} &\left< \frac{dP}{d\Omega} \right> = \frac{1}{4\pi c^3} \left( \frac{e^2 E_0}{m_e}\right)^2 \sin^2 \Theta \frac{1}{T} \int_0^T \cos^2 \omega_0 t dt = \frac{1}{4\pi c^3} \left( \frac{e^2 E_0}{m_e}\right)^2 \sin^2 \Theta \frac{1}{T} \int_0^T \frac{1}{2} (1-\cos 2\omega_0 t) dt \notag \\ &\overset{T \rightarrow \infty}{\longrightarrow} \frac{1}{8\pi c^3} \left( \frac{e^2 E_0}{m_e}\right)^2 \sin^2 \Theta \tag{3} \end{align}\]Thomson散乱の微分散乱断面積と古典電子半径
Rutherford散乱にならって、微分散乱断面積は以下のように定義できます。
\[\left< \frac{dP}{d\Omega} \right> = <S> \frac{d\sigma (\Theta)}{d\Omega} \tag{4}\](3)式は、両辺を光子1個あたりのエネルギー\(\hbar \omega\)で割ることで光子の数に変換し、\(d\Omega\)をかけると理解しやすくなります。すると左辺は散乱されて\(\Theta, \phi\)方向の微小立体角\(d\Omega\)から出ていく単位時間あたりの光子数、そして右辺が微小面積\(d\sigma(\Theta)\)に入射した光子数となります。
それではこれを具体的に計算しましょう。電磁場のエネルギーと運動量からポインティングベクトルは
より、この大きさの長時間平均は
\[<S> = \frac{1}{T} \int_0^T \frac{c}{4\pi}E_0^2 \cos^2\omega_0 t dt \overset{T \rightarrow \infty}{\longrightarrow} \frac{c}{8\pi} E_0^2 \tag{5}\](3), (4), (5)式より
\[\frac{d\sigma}{d\Omega} = \left(\frac{e^2}{m_e c^2} \right)^2 \sin^2 \Theta = r_0^2 \sin^2\Theta \tag{6}\]ここで\(r_0 = \frac{e^2}{m_e c^2}\)は古典電子半径と呼ばれる量です。これは電子が作る電場の自己エネルギー\(\frac{e^2}{r_0}\)と質量エネルギー\(m_e c^2\)が等しいと考えることで決まる電子の古典的な大きさです。具体的な数値としては
\[\frac{e^2}{m_e c^2} = \frac{e^2}{\hbar c} \frac{\hbar c}{m_e c^2} \sim \frac{1}{140} \frac{200 \mathrm{MeV} \cdot 1 \mathrm{fm}}{0.5 \mathrm{MeV}} \sim 3 [\mathrm{fm}]\]ですが、原子核の典型的な半径である1fmに比べると大きいことから、この見積もりの不正確さ(古典的な考え方の限界)がわかります。
Thomson散乱の散乱断面積
(6)式を全立体角で積分することで、散乱断面積を求めましょう。
\[\sigma_T = r_0^2 \int_0^{2\pi} d\phi \int_0^\pi \sin \Theta \sin^2 \Theta d\Theta \underbrace{=}_{\mu = \cos\Theta} 2\pi r_0^2 \int_{-1}^1 (1-\mu^2) d\mu = \frac{8\pi}{3} r_0^2 = 0.665 \times 10^{-24} [{\rm cm}^2]\]これはRutherford散乱の入射電子の速度を光速度\(c\)で置き換えたときの散乱断面積にほぼ一致しています。
Thomson散乱の特徴
ここにトムソン散乱の特徴をまとめます。
- 断面積は入射電磁波の周波数に依存しません。
- 散乱波の周波数は入射波の振動数と等しくなります。また断面積の導出方法から明らかなように、入射波の全エネルギーと散乱波の全エネルギーは等しくなります。すなわちトムソン散乱は弾性散乱であり、電磁波のエネルギーが散乱前後で保存します。言い換えると光子数と各々の光子のエネルギーが散乱前後で保存します。
- 入射波が\(\boldsymbol{\epsilon}\)方向に直線偏光している場合、散乱された電磁波は\(\boldsymbol{\epsilon}, \mathbf{n}\)の作る平面内に電場がある直線偏光になります。
- 後方・前方散乱対称性(Backward-Forward symmetry): \(\Theta \rightarrow \Theta + \pi\)にしても微分散乱断面積が変わりません。すなわち散乱されて入射波の進行方向に対して前方に出て行く光子数と後方に出て行く光子数が等しくなります。
特徴4は、散乱波の全運動量がゼロであることを意味しています。しかし、入射波はある一定の方向から入ってきたとしているので、有限の運動量を持っているはずです。すなわち散乱前後で電磁波の運動量が保存していません。
具体的に見てみましょう。
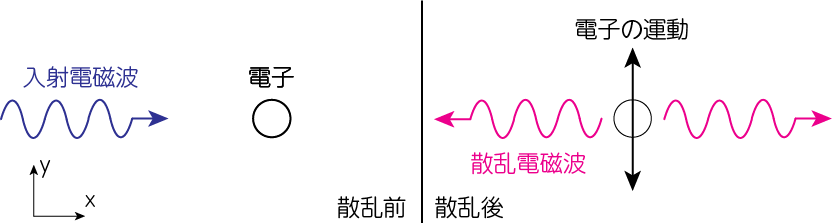
散乱前、電子が静止しているところに電磁波が入射してくるので、このときは右向き(\(x\)方向)の電磁波の運動量が存在します。これを\(\mathbf{p}_\mathrm{pre} = (p, 0)\)と書きましょう。トムソン散乱後は電子は上下方向に運動し、左右には同じ強度の電磁波が発生します(Backward-Forward symmetry)。すると散乱後の電子は\(y\)方向の運動量をもちます。これを\(\mathbf{p}_{\mathrm{post}, e} = (0, p’)\)、散乱電磁波の運動量は左右が打ち消し合い\(\mathbf{p}_{\mathrm{post, em}}=\mathbf{0}\)となります。このことから
\[\mathbf{p}_\mathrm{pre} \neq \mathbf{p}_{\mathrm{post}, e} + \mathbf{p}_\mathrm{post, em}\]です。よって運動量保存が破れていることがわかります。
これは電磁波による電子の運動方程式で、磁場によるローレンツ力を無視したことに起因しています。電磁波の運動量は磁場によって点電荷に伝えられます。電磁波は電場で点電荷をゆらしてエネルギーを伝え、揺れ出したら磁場で押して運動量を伝えているのです。したがって、磁場の効果を無視した時点で電磁波の運動量の伝搬が無視されたことになっています。運動量保存まで考慮した取り扱い、およびトムソン散乱の理論の適用限界についてはCompton散乱で学びましょう。
参考文献
[1] Rybicki & Lightman, “Radiative Processes in Astrophysics”
[2] 観山正見, 二間瀬敏史, 野本憲一, ”天体物理学の基礎 II”
[3] 中村文隆, 鶴剛, 長田哲也, 藤沢健太, 梅村雅之, 福江純, “放射素過程の基礎”