Table of contents
輻射によるプラズマ流の加速
X線星や活動銀河中心核、あるいはガンマ線バーストなどの高エネルギー天体現象では、非等方的な輻射場がプラズマに及ぼす力学的効果が重要となります。 極端な場合には、プラズマが相対論的速度まで加速される可能性もあり、相対論的ジェットの加速機構のひとつとして調べられてきました。 この機構を輻射加速と呼びます。
ここでは、この電子の輻射加速についてメモします。 前提知識として、特殊相対論を必要とします。
光子のエネルギー運動量テンソル
輻射場を光子の集団として記述することにしましょう。 光子分布が定常軸対称(例えば降着円盤の周辺など)だとして、対称軸を\(z\)軸にとることにします。
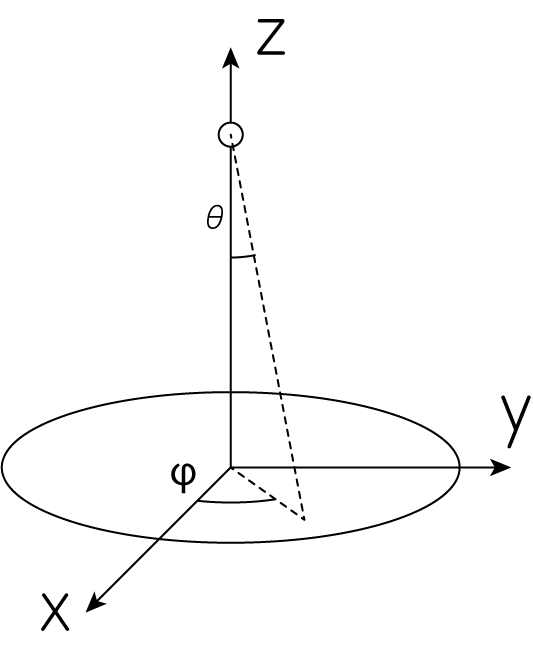
光子の位相空間分布関数を\(f(z, \mathbf{p})\)とします。 光子のエネルギー運動量テンソルは
\[T^{\mu \nu} (z) = \int f(z, \mathbf{p}) p^\mu p^\nu c^2 \frac{d^3 \mathbf{p}}{E} \tag{1}\]で定義されます。 ここで\(cp^\mu = (E, c\mathbf{p})\)は4元運動量、\(E\)は光子のエネルギー、そして\(\mathbf{p}\)は光子の3次元運動量です。 光子については
\[c^2 p^\mu p_\mu = E^2 - c^2 \mathbf{p}^2 = 0 \ \Longrightarrow \ E = cp \tag{2}\]が成り立ちます。 よって、光子の進行方向が\(z\)軸となす角を\(\theta\)としたとき
\[p_z = p \cos \theta = \frac{E}{c} \cos \theta \tag{3}\]と求まります。 これを用いて(1)式を計算しましょう。
\[T^{00} = \int f(z, \mathbf{p}) \frac{E}{c} \frac{E}{c} c^2 \frac{d^3 \mathbf{p}}{E} = \int f(z, \mathbf{p}) E d^3 \mathbf{p} \equiv J \tag{4}\] \[T^{03} = \int f(z, \mathbf{p}) p^0 p^3 c^2 \frac{d^3 \mathbf{p}}{E} = \int f(z, \mathbf{p}) \frac{E}{c} \frac{E}{c} \cos \theta c^2 \frac{d^3 \mathbf{p}}{E} = \int f(z, \mathbf{p}) E \cos \theta d^3 \mathbf{p} \equiv H \tag{5}\] \[T^{33} = \int f(z, \mathbf{p}) p^3 p^3 c^2 \frac{d^3 \mathbf{p}}{E} = \int f(z, \mathbf{p}) E \cos^2 \theta d^3 \mathbf{p} \equiv K \tag{6}\]ここで\(J, H, K\)はそれぞれ、エネルギー密度、\(z\)方向のエネルギー流束密度 (運動量密度)、\(z\)方向への輻射圧を表します。
\[\begin{align} T^{11} &= \int f(z, \mathbf{p}) p^1 p^1 c^2 \frac{d^3 \mathbf{p}}{E} = \int f(z, \mathbf{p}) E \sin^2 \theta \cos^2 \varphi d^3 \mathbf{p} \notag \\ &= \int f(z, \mathbf{p}) E (1-\cos^2 \theta) \cos^2 \varphi d^3 \mathbf{p} \end{align}\]ここで出てくる\(\varphi\)ですが、今は系が\(z\)軸に対して対称です。 よって\(\varphi=0\)としてしまっても、問題はないでしょう。 すると
\[T^{11} = \int f(z, \mathbf{p}) E (1-\cos^2 \theta) d^3 \mathbf{p} \underbrace{=}_{(4), (6)} J - K \tag{7}\]です。 同様に
\[T^{22} = \int f(z, \mathbf{p}) p^2 p^2 c^2 \frac{d^3 \mathbf{p}}{E} = J-K \tag{8}\]ですが
\[T_\mu ^{\ \ \mu} = \int f(z, \mathbf{p}) p_\mu p^\mu c^2 \frac{d^3 \mathbf{p}}{E} = 0\]でなければならないため、\(T^{11}, T^{22}\)にそれぞれ1/2をかけたものを最終的なエネルギー運動量テンソルとしましょう。 さらに
\[T^{01} = T^{10} = \int f(z, \mathbf{p}) E \sin \theta \cos \varphi d^3 \mathbf{p} = 0\] \[T^{12} = T^{21} = \int f(z, \mathbf{p}) E \sin^2 \theta \cos \varphi \sin \varphi d^3 \mathbf{p} = 0\]などから、光子のエネルギー運動量テンソルが
\[(T^{\mu \nu}) = \left( \begin{array}{cccc} J & 0 & 0 & H \\ 0 & \frac{1}{2} (J-K) & 0 & 0 \\ 0 & 0 & \frac{1}{2} (J-K) & 0 \\ H & 0 & 0 & K \end{array} \right) \tag{9}\]のように求まりました。
運動方程式
\(z\)軸上にある電子と光子のコンプトン散乱による相互作用を考えましょう。 ただし簡単のため、断面積はトムソン散乱断面積\(\sigma_\mathrm{T}\)で与えられるものとします。 1個の電子の受ける散乱頻度は、電子が静止して見える系で
\[c \sigma_\mathrm{T} \int f'(\mathbf{p}') d^3 \mathbf{p}' \tag{10}\]のように与えられます。 ここで\('\)は、電子の ここから、散乱で単位時間あたりに得る運動量は、1回の散乱で受ける\(z\)方向の平均の運動量移行とすると
\[\frac{dq_z'}{d\tau} = c \sigma_\mathrm{T} \int f'(\mathbf{p}') \Delta p_z' d^3 \mathbf{p}' \tag{11}\]と書くことができます。 ここで、光子の運動量\(p\)との混同を避けるため、電子の\(z\)方向の運動量を\(q_z\)としました。 1つの光子の衝突による散乱角を\(\theta_s'\)とすると、入射光子の運動方向への運動量輸送は\(\frac{E'}{c} (1-\cos \theta_s')\)となります。

これを散乱角で平均すると、結局
\[\Delta p_z' = \frac{1}{\pi} \int_0^\pi \frac{E'}{c} (1-\cos \theta_s') d\theta_s' = \frac{E'}{c} = p_z' \tag{12}\]のようになるため、運動方程式(11)は
\[\frac{dq_z'}{d\tau} = \sigma_\mathrm{T} H' \tag{13}\]のようになります。 電子が運動して見える元の座標系では、電子は速度\(v\)で\(z\)方向に運動しているとしましょう。 このとき、4元力は\(F^\mu = (0, 0, 0, \sigma_\mathrm{T} H')\)のように書かることから、元の座標系での4元力は、この4元力のローレンツ変換より
\[(\Lambda^\nu_{\ \ \mu} F^\mu) = \left( \begin{array}{cccc} \gamma & 0 & 0 & \frac{v}{c} \gamma \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \frac{v}{c} \gamma & 0 & 0 & \gamma \end{array}\right) \left( \begin{array}{c} 0 \\ 0 \\ 0 \\ \sigma_\mathrm{T} H' \end{array}\right) = \left( \begin{array}{c} \frac{v}{c} \gamma \sigma_\mathrm{T} H' \\ 0 \\ 0 \\ \gamma \sigma_\mathrm{T} H' \end{array}\right) \tag{14}\]のように計算されます。 以上から、元の座標系での電子の運動方程式が
\[\frac{d mc \gamma}{d\tau} = \gamma \frac{v}{c} \sigma_\mathrm{T} H' \tag{15}\] \[\frac{d mv \gamma}{d\tau} = \gamma \sigma_\mathrm{T} H' \tag{16}\]と求まります。 固有時間\(\tau = t / \gamma\)と(15)式より
\[\frac{d\gamma}{dt} = \frac{\sigma_\mathrm{T}}{mc^2} v H' \tag{17}\]ですが、これを\(z\)軸上の運動の軌跡に沿っての変化を考えると、\(dz = v dt\)より
\[\frac{d\gamma}{dz} = \frac{\sigma_\mathrm{T}}{mc^2} H' \tag{18}\]のように書くこともできます。 エネルギー運動量テンソルのローレンツ変換を計算しましょう。 すると
\[\begin{align} (T^{\mu \nu '}) &= (\Lambda^\mu_{\ \ \alpha} T^{\alpha \beta} \Lambda^\nu_{\ \ \beta} ) \notag \\ &= \left( \begin{array}{cccc} \gamma & 0 & 0 & -\beta \gamma\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ -\beta \gamma & 0 & 0 & \gamma \end{array}\right) \left( \begin{array}{cccc} J & 0 & 0 & H \\ 0 & \frac{1}{2} (J-K) & 0 & 0 \\ 0 & 0 & \frac{1}{2} (J-K) & 0 \\ H & 0 & 0 & K \end{array}\right) \left( \begin{array}{cccc} \gamma & 0 & 0 & -\beta \gamma\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ -\beta \gamma & 0 & 0 & \gamma \end{array}\right) \notag \\ &= \left( \begin{array}{cccc} \gamma J-\beta \gamma H & 0 & 0 & \gamma H-\beta \gamma K \\ 0 & \frac{1}{2} (J-K) & 0 & 0 \\ 0 & 0 & \frac{1}{2} (J-K) & 0 \\ -\beta \gamma J+\gamma H & 0 & 0 & -\beta \gamma H+\gamma K \end{array}\right) \left( \begin{array}{cccc} \gamma & 0 & 0 & -\beta \gamma\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ -\beta \gamma & 0 & 0 & \gamma \end{array}\right) \notag \\ &= \left( \begin{array}{cccc} \gamma^2 J-\beta \gamma^2 H - \beta \gamma^2 H + \beta^2 \gamma^2 K & 0 & 0 & -\beta \gamma^2 J + \beta^2 \gamma^2 H + \gamma^2 H - \beta \gamma^2 K \\ 0 & \frac{1}{2} (J-K) & 0 & 0 \\ 0 & 0 & \frac{1}{2} (J-K) & 0 \\ -\beta \gamma^2 J + \gamma^2 H + \beta^2 \gamma^2 H - \beta \gamma^2 K & 0 & 0 & \beta^2 \gamma^2 J - \beta \gamma^2 H - \beta \gamma^2 H + \gamma^2 K \end{array}\right) \tag{19} \end{align}\]より
\[H' = \gamma^2 \{ (1+\beta^2) H - \beta (J+K) \} \tag{20}\]となります。 加速が起こらない、すなわち(20)式がゼロとなるときを求めてみましょう。 そのときを\(\beta_\mathrm{eq}\)と書くことにします。 (20)式において、\(\beta > \beta_\mathrm{eq}\)のときは第二項から電子が減速され、\(\beta< \beta_\mathrm{eq}\)では第一項から電子は加速されます。
\[\begin{align} &H \beta^2 - (J+K) \beta + H = 0 \notag \\ &\Longrightarrow \ \beta_\mathrm{eq} = \frac{(J+K) \pm \sqrt{(J+K)^2 - 4H^2}}{2H} = \frac{1 \pm \sqrt{1-A^2}}{A} \quad \left( A \equiv \frac{2H}{J+K} \right) \tag{21} \end{align}\]\(0 \leq \beta < 1\)より、マイナス符号が\(\beta_\mathrm{eq}\)として用いることにします。 ここから
\[\begin{align} \gamma_\mathrm{eq}^2 &= \frac{1}{1-\beta^2} = \frac{1}{1 - \left( \frac{1-\sqrt{1-A^2}}{A} \right)^2} = \frac{1}{\frac{2A^2 + 2\sqrt{1-A^2} - 2}{A^2}} = \frac{A^2}{2 \sqrt{1-A^2} (1-\sqrt{1-A^2})} \notag \\ &= \frac{A^2 (1+\sqrt{1-A^2})}{2 \sqrt{1-A^2} (1 - 1 + A^2)} = \frac{1+\sqrt{1-A^2}}{2 \sqrt{1-A^2}} \tag{22} \end{align}\]のようになります。 (21), (22)式より、この輻射場で電子を相対論的速度まで加速するには、\(A\)が非常に1に近いことが必要です。 これはつまり、極めて方向のそろった、非等方的な輻射場が必要とわかります。
例: 降着円盤による輻射
ここでは降着円盤からの輻射によるプラズマの加速について考えてみましょう。 簡単のため、降着円盤を一様な明るさで輝く半径\(R\)の円盤とします。
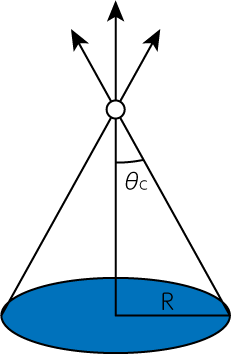
円盤の回転軸上で、円盤中心から距離\(z\)にある点から円盤を見込む半頂角を\(\theta_c\)とすると
\[\cos \theta_c = \frac{z}{\sqrt{R^2 + z^2}} \equiv \mu_c \tag{23}\]です。 この円盤を見込む立体角は
\[\Omega_c = \int_0^{2\pi} d\varphi \int_0^{\theta_c} \sin \theta d\theta = 2\pi (1- \mu_c) \tag{24}\]のように計算されます。 この点に到達する光子は、この立体角の範囲にしか存在しないと考えることができます。 この円盤からの放射強度は
\[I = c \int f(z, \mathbf{p}) E p^2 dp \tag{25}\]です。 ここから、エネルギー密度\(J\)は
\[J = \frac{1}{c} \int I d\Omega = \frac{2\pi I}{c} (1-\mu_c) \tag{26}\]エネルギー流束\(H\)は
\[\begin{align} H &= \frac{1}{c} \int I \cos \theta d\Omega = \frac{2\pi I}{c} \int_0^{\theta_c} \cos \theta \sin \theta d\theta \underbrace{=}_{\mu = \cos \theta} \frac{2\pi I}{c} \int_1^{\mu_c} (-\mu) d\mu = - \frac{\pi I}{c} [\mu^2]_1^{\mu_c} \notag \\ &= \frac{\pi I}{c} (1-\mu_c^2) \tag{27} \end{align}\]そして\(z\)方向の輻射圧は
\[\begin{align} K &= \frac{1}{c} \int I \cos^2 \theta d\Omega = \frac{2\pi I}{c} \int_0^{\theta_c} \cos^2 \theta \sin \theta d\theta \underbrace{=}_{\mu = \cos \theta} \frac{2\pi I}{c} \int_1^{\mu_c} (-\mu^2) d\mu = - \frac{2\pi I}{3c} [\mu^3]_1^{\mu_c} \notag \\ &= \frac{2\pi I}{3c} (1-\mu_c^3) \tag{28} \end{align}\]となります。 以上より
\[A = \frac{\frac{2\pi I}{c} (1-\mu_c^2)}{\frac{2\pi I}{c} (1-\mu_c) + \frac{2\pi I}{3c} (1-\mu_c^3)} = \frac{3(1+\mu_c)}{4 + \mu_c + \mu_c^2} \tag{29}\]を得ます。 \(z = 0\)では、\(\mu_c = 0\)より
\[A = \frac{3}{4}, \quad \beta_\mathrm{eq} = \frac{4 - \sqrt{7}}{3} \sim 0.45, \quad \gamma_\mathrm{eq}^2 = \frac{7 + 4\sqrt{7}}{14} \sim 1.26 \tag{30}\]のように、光速の半分程度までしか加速されないことがわかります。 これをジェットのマジックスピードと呼ぶこともあります。
遠方では\(\mu_c \rightarrow 1\)となるため、輻射場の方向が揃うことになります。 \(\mu_c, A\)を\(\left( \frac{R}{z} \right)^2\)でテイラー展開しましょう。 すると
となります。 これだけ見ると\(\gamma_\mathrm{eq}\)は、\(z\)とともに増大することがわかります。 しかし
\[H' \approx \frac{2\pi I}{c} \left( \frac{R}{z} \right)^2 \gamma^2 \left\{ \frac{1}{8\gamma^4} - \frac{1}{24} \left( \frac{R}{z} \right)^4 \right\} \tag{34}\]のように、輻射場も距離とともに弱くなることがわかります。 \(z_t\)程度の距離まで加速され、そこから加速が起こらなくなると、そのときの終端ローレンツ因子\(\gamma_t\)は
\[\gamma_t^4 \approx 3 \left( \frac{z_t}{R}\right)^4 \tag{35}\] \[\frac{d\gamma}{dz} \approx \frac{\gamma_t}{z_t} = \frac{\sigma_\mathrm{T}}{m c^2} \frac{2\pi I}{c} \left( \frac{R}{z_t}\right)^2 \frac{1}{8\gamma_t^2} \ \Longrightarrow \ \gamma_t \approx \left( \frac{3^{1/4} \sigma_\mathrm{T} \pi I R}{4mc^3} \right)^{1/4} \tag{36}\]のように評価されます。 今の場合、円盤の全光度は\(L = 2\pi^2 R^2 I\)より
\[\gamma_t \approx \left( \frac{3^{1/4} \sigma_\mathrm{T} L}{8\pi mc^3 R} \right)^{1/4} \tag{37}\]のように書くこともできます。 ここで\(L/R\)はコンパクトネスパラメータと呼ばれる量で、\(4\pi mc^3 / \sigma_\mathrm{T} \sim 4.7 \times 10^{29} \mathrm{erg/s/cm}\)の単位で測られます。 高エネルギー天体では\(1 \sim 10^3\)という値が典型的ですが、(37)式から\(\gamma_t\)はその\(1/4\)乗の依存性であるため、それほど大きくなることはありません。 そしてこの評価は、電子1個に対するものです。 プラズマが電子・陽電子対のみから構成されるときには適用可能ですが、陽子など別の質量の荷電粒子が存在する場合、慣性が陽子と電子の質量比の分だけ大きくなるため、相対論的速度まで加速するのは困難となります。 さらにここでの説明は輻射場は外部から与えられたものとしており、物質が輻射場に及ぼす影響が無視されています。 したがって、これはいわゆる光学的に薄い場合にのみ成立する議論です。 輻射場が物質によって閉じ込められるような光学的に厚い場合には、粒子ではなく、流体力学的な取り扱いが必要となります。 この極限はファイアーボールと呼ばれ、相対論的速度への加速の有力な候補として知られています。
参考文献
[1] Icke, 1989, “Photon surfing near compact accreting objects”
[2] 高原文郎, “特殊相対論”
[3] 柴田一成, 福江純, 松元亮治, 嶺重慎, “活動する宇宙”