Table of contents
X線パルサー
アルヴェーン半径
降着流が球対称であると仮定しましょう。 中心にいる中性子星の質量を\(M\)、半径を\(R\)としましょう。 中性子星が双極子磁場を持っているとして
\[B \approx \frac{\mu}{r^3} \tag{1}\]のように書けるとします。 ここで\(\mu = B_s R^3\)は磁気双極子モーメント、\(r\)は中心星からの距離です。 すると、この双極子磁場による磁気圧は
\[P_\mathrm{mag} = \frac{B^2}{8\pi} = \frac{\mu^2}{8\pi r^6} \tag{2}\]となります。 中心にいる中性子星への降着が定常的であり、\(\dot{M} = 4\pi r^2 \rho v\)が一定であるとしましょう。 磁気圧と降着ガスの動圧 (ram presure) \(P_\mathrm{ram} = \rho v^2\)が等しくなる半径を、\(r_M\)としましょう。 そして降着ガスの自由落下速度を \(v_\mathrm{ff}= \sqrt{2GM/r}\)とします。 すると
\[\begin{align} &\frac{\mu^2}{8\pi r_M^6} = \rho v^2 = \vert \rho v \vert v_\mathrm{ff} = \frac{\dot{M}}{4\pi r_M^2} \sqrt{\frac{2MG}{r_M}} \notag \\ &\Longrightarrow \ r_M^\mathrm{(sph)} = \left( \frac{\mu^4}{8GM\dot{M}^2}\right)^{1/7} \simeq 5.1 \times 10^8 \dot{M}_{16}^{-2/7} m_1^{-1/7} \mu_{30}^{4/7} \ [\mathrm{cm}] \tag{3} \end{align}\]のようになります。 ここで\(\dot{M}_{16} \equiv \dot{M} / (10^{16} \mathrm{g/s}), m_1 = M/M_\odot, \mu_{30} = \mu / (10^{30} \mathrm{G \ cm^2})\)です。 \(\mu = 10^{30} \mathrm{G \ cm^2}\)は、\(B_s = 10^{12} \mathrm{G}, R = 10^6 \mathrm{cm}\)に対応します。 この\(r_M\)をアルヴェーン半径 (Alfvén radius)と呼びます。
ここで、降着ガスが重力エネルギーを解放することにより放出される光度を\(L_\mathrm{acc} = GM\dot{M} / R\)として、\(\dot{M}\)を消去すると
のようにも整理できます。 ここで、\(R_6 = R/10^6 \mathrm{cm}, L_{37} = L_\mathrm{acc} / 10^{37} \mathrm{erg/s}\)です。
円盤降着に対しては、アルヴェーン半径は
のように経験的に近似されます。 \(M \sim M_\odot, R \sim 10^6 \mathrm{cm}\)のような典型的な中性子星のとき、\(r_M^\mathrm{(disc)} < R\)となる臨界磁場強度を\(B_{s:\mathrm{crit}}\)としましょう。 そして\(L_\mathrm{acc} \sim 10 L_\mathrm{Edd} \sim 1.2 \times 10^{39} \mathrm{erg/s}\)とすると
\[B_{s:\mathrm{crit}} \sim 1.7 \times 10^9 \ [\mathrm{G}] \tag{6}\]のようになります。 \(B_s < B_{s: \mathrm{crit}}\)の場合、双極子磁場が降着に与える影響は少ないと考えることができます。
Fastness parameter と共回転半径
次に、中性子星の双極子磁場が、中性子星のスピン角速度\(\Omega_\ast\)と同じ角速度で共回転している場合を考えましょう。 先ほどのアルヴェーン半径より内側\((r \lesssim r_M)\)を中性子星磁気圏とし、そこに存在する物質は磁場と強く相互作用しているために、磁力線に沿った方向にしか運動できないとします。 さらに磁気圏より外側 \((r \gtrsim r_M)\)にいる降着物質は、ケプラー回転による円盤を形成しており、その速度は
\[v_\varphi \approx r \Omega_K (r) = \sqrt{\frac{GM}{r}} \tag{7}\]であるとします。 この設定で、\(r = r_M\)で降着物質に働く力について考えてみましょう。 共回転する磁気圏から見ると、アルヴェーン半径にいる降着物質には、遠心力\(r_M \Omega_\ast^2\)が働きます。 物質が中性子星に降着するには、重力が遠心力より大きくなければなりません。 よって
\[r_M \Omega_\ast^2 < r_M \Omega_K^2 (r_M) \ \Longrightarrow \ \omega_\ast \equiv \frac{\Omega_\ast}{\Omega_K (r_M)} < 1 \tag{8}\]とわかります。 この\(\omega_\ast\)をfastness parameterと呼びます。 外側から降着する物質の角速度が、共回転する磁気圏と同じ角速度になる半径を、共回転半径 \(r_\Omega\)としましょう。 すなわち
\[\Omega_K (r_\Omega) = \Omega_\ast = \frac{2\pi}{P_\ast} \ \Longrightarrow \ r_\Omega = \left( \frac{GM P_\ast^2}{4\pi^2}\right)^{1/3} \simeq 1.5 \times 10^8 P_\ast^{2/3} m_1^{1/3} \ [\mathrm{cm}] \tag{9}\]ここで、\(P_\ast = \frac{2\pi}{\Omega_\ast}\)は中性子星の自転周期です。 \(r = r_M\)でガスが遠心力により離れていかないためには
\[\Omega_K (r_\Omega) = \Omega_\ast < \Omega_K (r_M) \ \Longrightarrow \ r_\Omega > r_M \tag{10}\]であることもわかります。
平衡状態での自転周期
中性子星への質量降着が非常に長い時間に渡って行われると、降着物質が持つ角運動量により中性子星の自転が速くなることが考えられます。 \(r = r_M\)での重力と遠心力が等しくなるとき、物質は降着を起こさなくなると考えることができます。 (8)式の\(\omega_\ast = 1\)から
\[\begin{align} P_\mathrm{eq} &\equiv \frac{2\pi}{\Omega_K (r_M)} = \frac{2\pi}{\sqrt{GM}} r_M^{3/2} \simeq \frac{2\pi}{\sqrt{G m_1 M_\odot}} (0.5 \times 2.9 \times 10^8 m_1^{1/7} R_6^{-2/7} L_{37}^{-2/7} \mu_{30}^{4/7})^{3/2} \notag \\ &\simeq 1.0 m_1^{-2/7} R_6^{-3/7} L_{37}^{-3/7} \mu_{30}^{6/7} \ [\mathrm{s}]\tag{11} \end{align}\]のように求まります。 これは、質量降着をしている強磁場中性子星の最小自転周期とも言えます。 \(L = L_\mathrm{Edd} = 1.3 \times 10^{38} \mathrm{erg/s}, M=M_\odot, R = 10^6 \mathrm{cm}\)の場合
\[P_\mathrm{eq} \simeq 2 \times 10^{-3} B_9^{6/7} \ [\mathrm{s}] \tag{12}\]のようになります。 ここで\(B_9 = B/10^9 \mathrm{G}\)であり、\(\mu = B R^3\)を用いました。 (12)式を\(P_\mathrm{eq} \propto B\)のように近似しましょう。 さらに、双極子放射から導出した磁場と自転周期\(P\)と自転周期の変化率\(\dot{P}\)の関係式
\[B = \sqrt{\frac{3c^2 I}{2\pi^2 R^6} P \dot{P}} \tag{13}\]を用いると
\[\dot{P}_\mathrm{spinup} \simeq 5 \times 10^{-16} R_6^6 I_{45}^{-1} P_\mathrm{eq} \tag{14}\]のようになります。 \(P-\dot{P}\)平面に中性子星をプロットすると、このスピンアップの直線が現れることを示しています。
質量降着による強磁場を持つ中性子星のスピンアップ
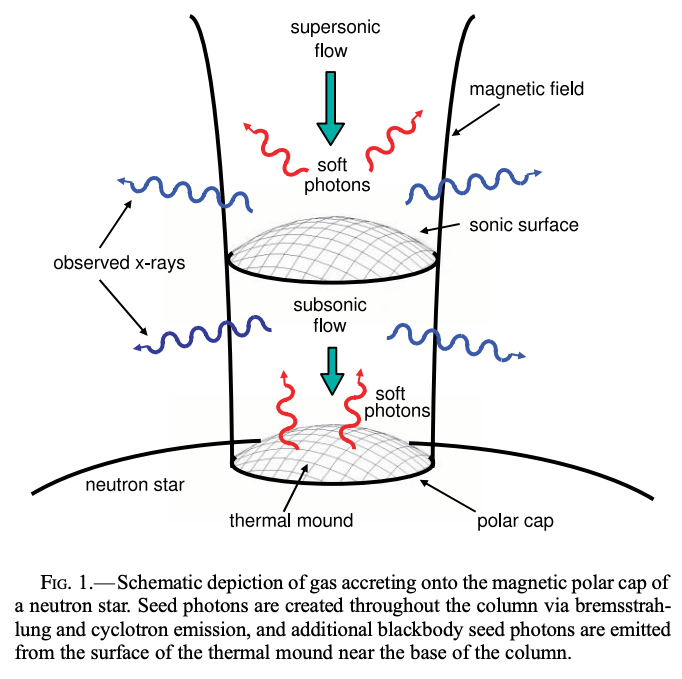
中性子星表面での磁場が\(B \gtrsim B_{s: \mathrm{crit}} \sim 10^9 \mathrm{G}\)の場合、アルヴェーン半径\(r_M\)が中性子星半径\(R\)より大きくなり、中性子星磁気圏の磁場が降着流に強く影響を与えます。 自転する中性子星と共回転する(双極子)磁場に貫かれた磁気圏では、プラズマは磁力線に沿った方向に運動します。 そのため、降着円盤の降着流は磁力線に沿って、中性子星磁極方向に集まります。 このようにして磁極領域に形成される降着柱 (accretion column)は、圧縮され高温度になり、X線やγ線を放出します。 磁軸と自転軸が一致していない場合、磁極にある降着柱からの高エネルギー放射が自転周期とともに変化し、X線がパルスのように見えるX線パルサーとして観測されます。
スピンが平衡状態になる前の\(\omega_\ast < 1\)の場合、アルヴェーン半径に位置する降着円盤中のガスの軌道運動速度は、磁場の共回転速度を上回っています。 共回転速度と軌道運動速度が同じ方向の場合、\(r \sim r_M\)の降着ガスが共回転磁気圏にトルクを与え、スピンアップさせます。 このトルクが内部へと伝わり、最終的に中性子星をスピンアップさせることになります。 したがって、ガスが降着円盤の内側に移動するにつれて、軌道運動の速度\(v_\varphi\)が\(r_M \Omega_K (r_M)\)から\(r_M \Omega_\ast\)に急激に変化するような遷移領域が、\(r_M\)付近に存在することになります。 (磁気圏内のプラズマと磁場は中性子星とともに共回転していることを仮定しています。したがって磁場のトロイダル成分 \(B_\varphi\)は\(r \sim r_M\)付近の遷移領域で生成されることに注意が必要です。)
今、その遷移領域の幅を\(\delta (\ll r_M)\)とすると、自転する中性子星の角運動量の満たす方程式は
となります。 ここで\(I\)は中性子星の慣性モーメント、\(N\)は遷移領域の外側からくるトルク、そして\(\ell_0 = \sqrt{GM r_M}\)は\(r = r_M\)での単位質量あたりの角運動量です。 \(N\)が無視できるとすると
\[\begin{align} \dot{\nu} &= \frac{1}{2\pi} \frac{d\Omega_\ast}{dt} = \frac{\dot{M} \ell_0}{2\pi I} \notag \\ &\simeq \frac{R L_\mathrm{acc}}{2\pi I} \sqrt{\frac{r_M}{GM}} \underbrace{\simeq}_{(4)} \frac{10^{43} R_6 L_{37}}{2\pi \times 10^{45} I_{45}} \sqrt{\frac{0.5 \times 2.9 \times 10^8}{6.67 \times 10^{-8} \times 2 \times 10^{33} m_1 }} m_1^{1/14} R_6^{-1/7} L_{37}^{-1/7} \mu_{30}^{2/7} \notag \\ &\simeq 1.8 \times 10^{-12} m_1^{-3/7} R_6^{6/7} L_{37}^{6/7} \mu_{30}^{2/7} I_{45}^{-1} \ [\mathrm{Hz/s}] \tag{16} \end{align}\]のようになります。 ここで\(I_{45} = I / 10^{45} \mathrm{g/cm^2}\)であり、途中\(L_\mathrm{acc} = GM \dot{M} / R\)を用いました。 すると
\[P = \frac{2\pi}{\Omega} = \frac{1}{\nu} \ \Longrightarrow \ \dot{P} = - \frac{\dot{\nu}}{\nu^2} = - P^2 \dot{\nu} \tag{17}\]より
\[\begin{align} - \frac{\dot{P}}{P} &= P \dot{\nu} \simeq 1.8 \times 10^{-12} m_1^{-3/7} R_6^{6/7} \mu_{30}^{2/7} I_{45}^{-1} P L_{37}^{6/7} [\mathrm{s}^{-1}] \notag \\ &\simeq 5.7 \times 10^{-5} m_1^{-3/7} R_6^{6/7} \mu_{30}^{2/7} I_{45}^{-1} P L_{37}^{6/7} [\mathrm{yr}^{-1}] \tag{18} \end{align}\]となります。 スピンアップ率 \(- \dot{P} / P\)が、\(P L^{6/7}\)に比例していることがわかります。
降着柱
ここまで議論してきたように、強い磁場をもつ中性子星への降着はアルヴェーン半径で堰き止められ、磁力線に沿って磁極領域に流れていきます。
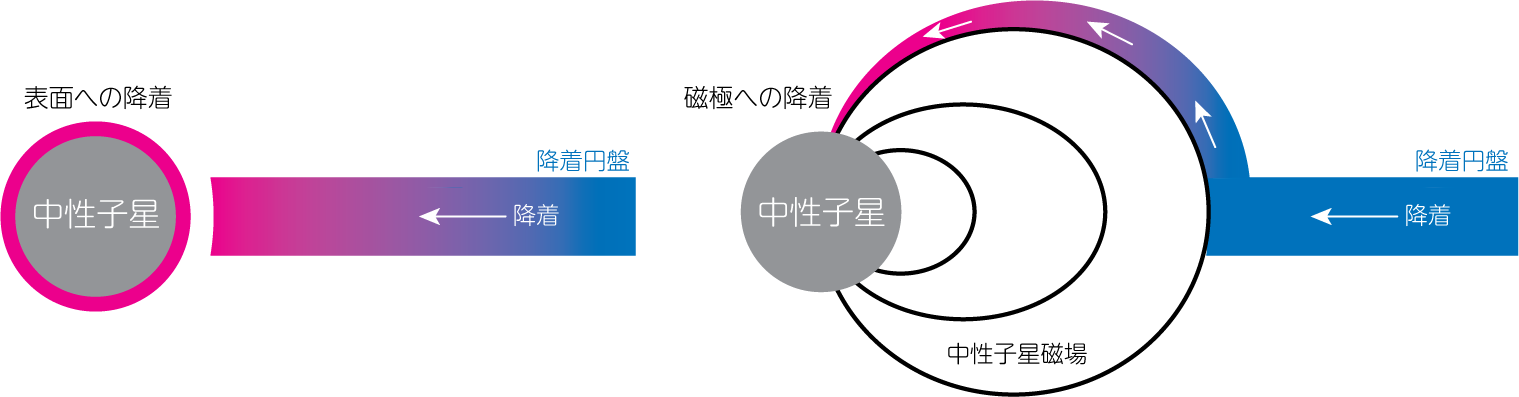
それぞれ弱磁場の中性子星への降着と、強磁場の中性子星への降着の様子。
ここでは、磁軸と回転軸が揃っていない強磁場を持つ中性子星について考えてみましょう。 簡単のため、中性子星磁場は双極子磁場であるとします。
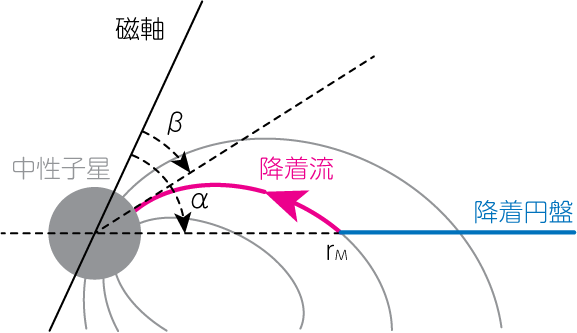
\(\theta\)を磁軸からの角度とすると、双極子磁場の曲線の方程式は
\[r = C \sin^2 \theta \tag{19}\]です。 磁力線と降着円盤が\(r = r_M\)で、角度\(\theta = \alpha\)で交差しているとすると
\[C = \frac{r_M}{\sin^2 \alpha} \tag{20}\]と求まります。 この磁力線が、\(r = R, \theta = \beta\)のように中性子星表面に根付いているとすると
\[\sin^2\beta = \frac{R}{C} = \frac{R}{r_M} \sin^2 \alpha \tag{21}\]のようになります。
降着物質が、\(\pi R^2 \sin^2 \beta\)の面積領域に降着するとしましょう。 この降着領域と中性子星表面との面積比は
のようになります。 (22)式の\((\cdots )\)は、2つの磁極を考慮した場合のものです。 もし磁場がとても強い場合、降着物質は磁極領域の限られた面積部分に集まり、そこで重力エネルギーを解放することになります。
降着円盤から磁力線に沿ってガスが降着すると、磁極領域にガスが集まり、降着柱を形成します。 磁力線に沿って物質が降着すると、その途中でガスは超音速となり、衝撃波を形成すると考えられます。
このときのガスの落下速度を\(v \sim v_\mathrm{ff} = \sqrt{2GM/R} \sim c/2\)、そして\(L_\mathrm{acc} \sim L_\mathrm{Edd}\)としましょう。 すると、この降着ガスを構成するプラズマ中の陽子の平均自由行程は
\[\lambda_d \equiv \frac{m^2 v^4}{2\pi n e^4 \ln \Lambda} \gtrsim 5 \times 10^9 \ [\mathrm{cm}] \gg R_\ast \sim 10^6 \ [\mathrm{cm}] \tag{23}\]と求まります。 ここでクーロン対数は\(\ln \Lambda \sim 20\)としました。
もしこの降着柱部分で衝撃波が発生した場合、平均自由行程がとても長いため、この設定では衝突による衝撃波を形成することができません。 衝撃波の厚みは平均自由行程\(\lambda_d\)より十分小さいため、このときにできる衝撃波は無衝突衝撃波ということになります。 最近でこそ無衝突衝撃波についてのPICシミュレーションなどが盛んに行われるようになりましたが、磁場がない場合ですら、無衝突衝撃波についてはまだよく理解されていません。 無衝突衝撃波の主な問題は、秩序だったエネルギーを拡散しランダム化するために、粘性以外の過程が必要となることです。 もう一つの困難な点として、質量降着率が大きくない場合でも、放射圧が降着流のダイナミクスに大きく影響する可能性があることです。 さらには、中性子星への降着の場合、強磁場を適切に考慮する必要があります。
ここではその困難な詳細を省いて、これまでに研究されてきた降着柱の理論モデルについて見ていきましょう。 主に3つのモデルが存在します。
- エディントン降着率を下回る場合 \((L_\mathrm{acc} < L_\mathrm{Edd})\)。放射圧無視、降着流中に衝撃波も存在しない。
- エディントン降着率を下回る場合 \((L_\mathrm{acc} < L_\mathrm{Edd})\)。放射圧無視、降着流中に無衝突衝撃波が存在する。
- エディントン降着率を上回る場合 \((L_\mathrm{acc} > L_\mathrm{Edd})\)。放射圧がガス圧を上回り、ガスが中性子星表面に落ち込むのをせき止める。光子と電子の衝突が起こるため、電子とともに動いている陽子も減速する。
以降では、3番目のケースについて簡単に議論していきましょう。 降着柱での放射場のエネルギー密度は\(U_\mathrm{rad}\)で、放射圧は\(P_\mathrm{rad} = U_\mathrm{rad}/3\)とします。 放射圧はガスを膨張させますが、中性子星磁場による磁気圧は降着流を圧縮し、狭い領域に閉じ込めます。 しかし簡単のため、ここでは磁場の応力は運動量保存方程式では無視することにしましょう。 定常的な流れを考えると
\[-A \rho v = \dot{M} = \mathrm{Const.} \tag{24}\] \[\rho v \frac{\partial v}{\partial z} + \frac{1}{3} \frac{\partial U_\mathrm{rad}}{\partial z} + g \rho = 0 \tag{25}\]となります。 ここで質量降着率\(\dot{M}\)は定数とし、降着を起こしている磁極領域の面積を\(A = 4\pi R^2 f_\mathrm{disk}\)としました。 (25)式でさらに重力を無視すると、(25)式は積分することができます。
\[U_\mathrm{rad} = 3 \rho \vert v \vert (v_\mathrm{ff} - v) = 3 \vert \rho v \vert v_\mathrm{ff} (1 - Q^{1/2}) = 3 \rho v_\mathrm{ff}^2 (Q^{1/2} - Q) \tag{26}\]ここで\(Q = v^2 / v_\mathrm{ff}^2\)です。
ガスは下向きに落下していくため、優先的に下向きに放射を散乱させます。 この効果による放射流束の修正を考慮すると
のようになります。 ここで\(\kappa = \sigma_T / m_p\)は、水素のみから構成されるプラズマガスでの電子散乱による不透明度です。 ガスの落下による運動エネルギーの減少が、即座に全て放射に変換されるとすると
\[\nabla \cdot \mathbf{F} = - \rho \mathbf{v} \cdot \nabla \left( \frac{v^2}{2} \right) = - \rho v \frac{\partial }{\partial z} \left( \frac{v^2}{2}\right) \tag{28}\]とすることができます。 これらの式を用いると、以下のような\(Q\)に対する偏微分方程式を得ることができます。
\[\nabla^2 Q = \frac{\sigma_T \rho \vert v \vert}{c m_p} \frac{\partial}{\partial z} (6 Q^{1/2} - 5Q) \tag{29}\]この微分方程式を、\(z=0, \infty\)そして\(r=r_c\) (降着柱の半径) での境界条件のもとで積分をすれば、\(Q\)を求めることができます。
次の図は、横軸\(\kappa S r / c\)、縦軸\(\kappa S z/c\)のQの等高線を示したものです。
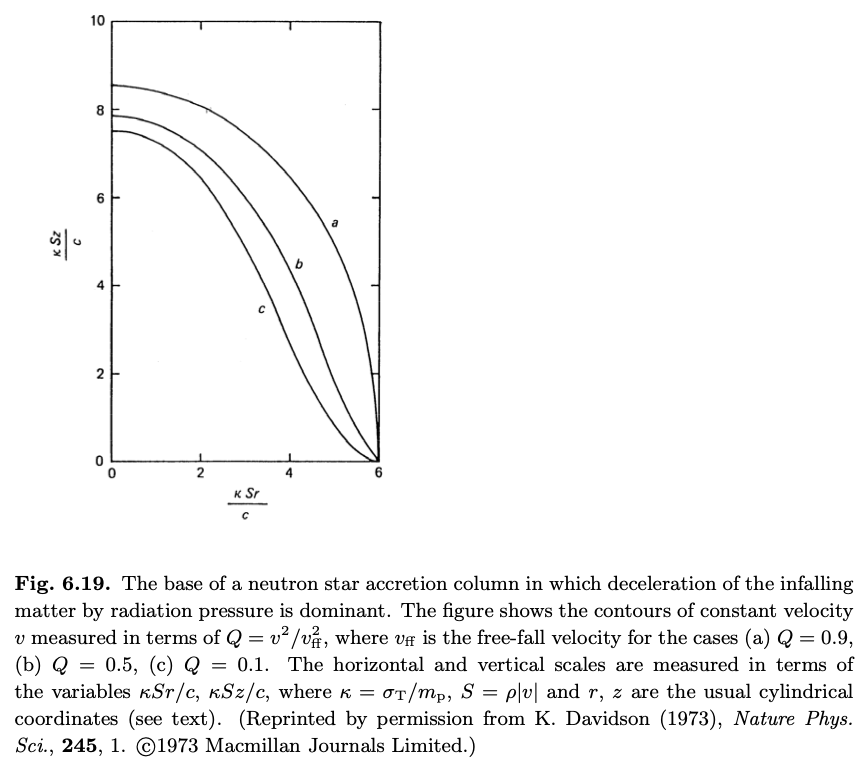
Davidson (1973)より。a, b, cはそれぞれ\(Q=0.9, 0.5, 0.1\)の等高線を表す。
典型的な値\(r_c = 10^5 \mathrm{cm}, \dot{M} = 10^{17} \mathrm{g/s}, v = c/2\)に対し、降着柱の底での温度\(T_b\)を求めてみましょう。 すると\(\rho \vert v \vert = 3 \times 10^6 \mathrm{g/cm^2/s}\)であり、\(U_\mathrm{rad} = 1.4 \times 10^{17} \mathrm{erg/cm^3}\)となります。 降着柱の底での光学的厚みが、放射場を熱化させるのに十分大きいとすると
\[T_b = \left( \frac{c}{4\sigma_\mathrm{SB}} U_\mathrm{rad} \right)^{1/4} \sim 6.6 \times 10^7 \ [\mathrm{K}] \tag{30}\]と求まります。 この温度は、観測されるX線放射を十分説明することができます。
最近の研究
X線パルサーの新しい描像
これまで考えられてきたX線パルサーの描像は、中性子星の磁極方向に光のビームが出るというものです。 磁極を正面から覗き込めるときにのみ、中性子星からの光を観測することができます。 これは宇宙灯台のモデルと呼ばれ、これまで長らく考えられてきました。
それに対し、Kawashima et al. (2016)では降着柱の輻射流体シミュレーションを行い、これまでと異なる宇宙灯台モデルを提案しました。 この研究で新しく提案されたのは、降着柱の側面が明るく輝くモデルです。
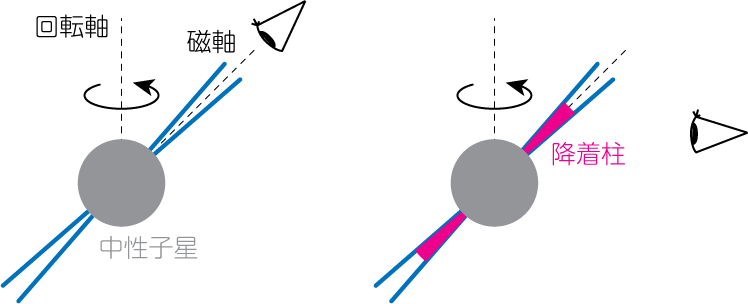
左図は既存の宇宙灯台モデル、右図は新しいモデル。既存モデルは磁軸領域を見たときのみ眩しく見えるのに対し、新モデルは降着柱の側面が多く見えるときに眩しく見える。
このモデルを考慮することで、これまではブラックホールと考えられてきた超高光度X線源 (Ultra-Luminous X-ray souces: ULXs)が、中性子星パルサーでも説明がつくことを示したのです。

Kawashima et al. (2016)より。超臨界降着により形成される降着柱の、ガス密度と放射エネルギー密度のカラーコントア。右端のパネルは放射光度の動径分布を表したもの。
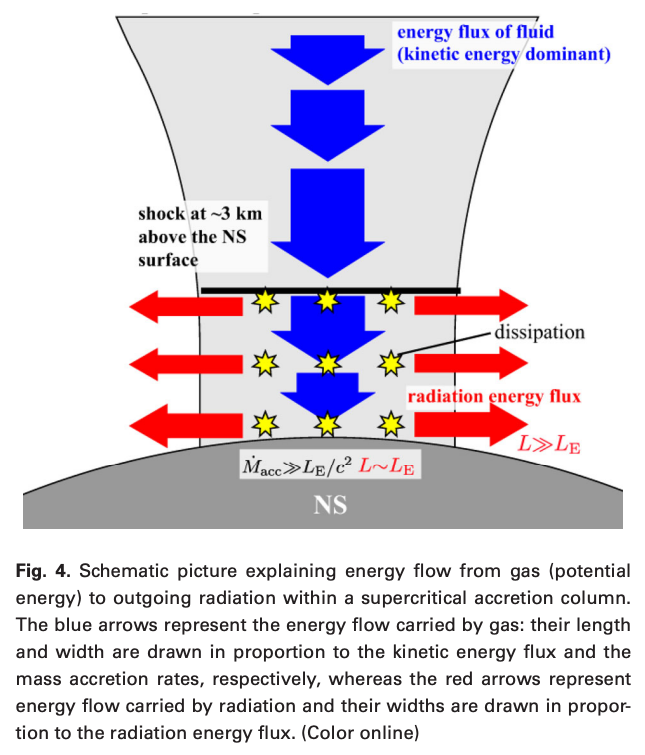
Kawashima et al. (2016)より。降着柱の側面からエネルギーが流出する概念図。
一般相対論的磁気流体シミュレーション
同じくシミュレーション研究ですが、Inoue et al. (2023)では一般相対論の効果も含めた磁気流体計算を実施しました。 しかも、先ほどは降着柱の部分のみを計算していましたが、こちらの研究では降着円盤部分も含めた中性子星表面への降着の様子を3次元シミュレーションし、降着率による降着柱と磁気圏の
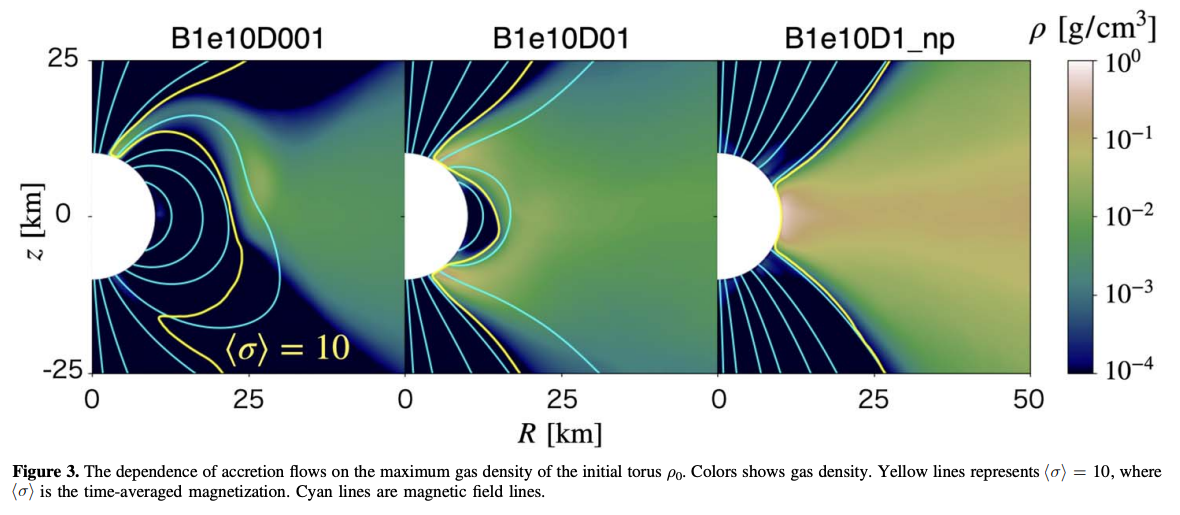
Inoue et al. (2023)より。左パネルから、降着率(初期トーラスのガス密度)が小さな順に計算結果を並べたもの。
降着率が小さいと降着柱が形成されていますが、降着率が大きい場合には磁気圏が消失していることがわかります。
参考文献
[1] Becker & Wolff, 2007, “Thermal and Bulk Comptonization in Accretion-powered X-Ray Pulsars”
[2] Davidson, 1973, “Accretion at a Magnetic Pole of a Neutron Star”
[3] Kawashima et al., 2016, “A radiation-hydrodynamics model of accretion columns for ultra-luminous X-ray pulsars”
[4] Inoue et al., 2023, “Modeling of Thermal Emission from ULX Pulsar Swift J0243.6+6124 with General Relativistic Radiation MHD Simulations”
[5] Frank, King, Raine, “Accretion Power in Astrophysics”
[6] Longair, “High Energy Astrophysics”
[7] 小山勝ニ, 嶺重慎, “ブラックホールと高エネルギー現象”