Table of contents
内部重力波 (internal gravity wave)
相対論の重力波(gravitational wave)とは異なるものなのでご注意ください。
直感的な導出
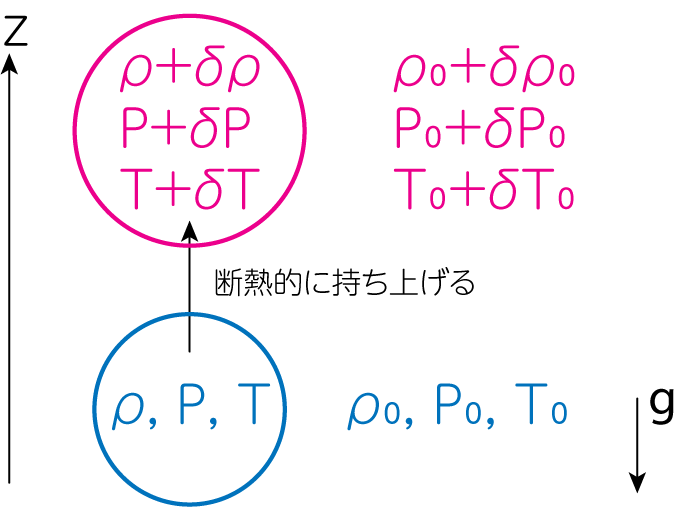
まずは直感的な議論から入りましょう。ある流体中の塊を考え、それを\(\delta z\)だけ持ち上げたとします。持ち上げる時には常に周囲と圧力平衡を保ちながら上昇させ、持ち上げる流体の塊は断熱的に密度変化すると仮定します(すなわち周囲との熱のやり取りを行わないくらい素早く持ち上げます)。持ち上げた流体の外側の物理量に0の添字をつけて考えると、周囲は
\[\frac{dP_0}{dz} = - \rho_0 g \tag{1}\]のように重力と圧力勾配による力の釣り合いが成り立っているとします。高さ\(z + \delta z\)における外側の圧力\(P_0 + \delta P_0\)と密度\(\rho_0 + \delta \rho_0\)より
\[P_0 (z + \delta z) = P_0 + \delta P_0 = P_0 + \frac{d P_0}{dz} \delta z \underbrace{=}_{(1)} P_0 - \rho_0 g \delta z \ \Longrightarrow \ \delta P_0 = -\rho_0 g \delta z \tag{2}\] \[\rho_0 (z + \delta z) = \rho_0 + \delta \rho_0 = \rho_0 + \frac{d\rho_0}{dz} \delta z \ \Longrightarrow \ \delta \rho_0 = \frac{d\rho_0}{dz} \delta z \tag{3}\]添字のなしを持ち上げられた流体の塊の内部の物理量とすると、周囲と圧力平衡を保ちながら持ち上げる仮定より
\[\delta P = \delta P_0 = - \rho_0 g \delta z \tag{4}\]ここで初期状態は\(P= P_0, \rho=\rho_0\)です。そこから断熱的に持ち上げたので
\[\begin{aligned} &P_0 = K \rho_0^\gamma \ \Longrightarrow \ \mathrm{const.} = \frac{P_0}{\rho_0^\gamma} = \frac{P_0 + \delta P}{(\rho_0 + \delta \rho)^\gamma} = \frac{P_0 + \delta P}{\rho_0^\gamma} \left( 1 + \frac{\delta \rho}{\rho_0}\right)^{-\gamma} \simeq \frac{P_0 + \delta P}{\rho_0^\gamma} \left( 1 - \frac{\gamma \delta \rho}{\rho_0}\right) \\ &\Longrightarrow \ P_0 = (P_0 + \delta P) \left( 1-\frac{\gamma \delta \rho}{\rho_0}\right) \simeq P_0 - \frac{\gamma P_0}{\rho_0} \delta \rho + \delta P \end{aligned}\]のようになります。この式と(4)式、さらに音速\(C_s^2 = \gamma P_0 / \rho_0\)を合わせて
\[\delta \rho = - \frac{\rho_0 g}{C_s^2} \delta z \tag{5}\](3), (5)式から、断熱的に持ち上げた流体の塊とその外側では密度が違うことがわかります。それにより流体の塊に働く浮力は
\[g (\delta \rho_0 - \delta \rho) = g\left( \frac{1}{\rho_0} \frac{d\rho_0}{dz} + \frac{g}{C_s^2} \right) \delta z = - N^2 \rho_0 \delta z \tag{6}\]ここで
\[N^2 \equiv - g \left( \frac{d\rho_0}{dz} + \frac{\rho_0 g}{C_s^2} \right) \tag{8}\]のように定義し、この\(N\)をBrunt-Väisälä周波数と呼びます。(8)式を変形し、物理的な理解を深めてみましょう。状態方程式より
\[P_0 = \frac{\rho_0}{\mu m_p} k_B T_0 \ \Longrightarrow \ \frac{dP_0}{dz} = \frac{k_B}{\mu m_p} T_0 \frac{d\rho_0}{dz} + \frac{k_B}{\mu m_p} \rho_0 \frac{dT_0}{dz}\](1)式より
\[- \rho_0 g = \frac{k_B}{\mu m_p} T_0 \frac{d\rho_0}{dz} + \frac{k_B}{\mu m_p} \rho_0 \frac{dT_0}{dz} \ \Longrightarrow \ \frac{1}{\rho_0} \frac{d\rho_0}{dz} = \frac{1}{T_0} \left( - g \frac{\mu m_p}{k_B} - \frac{dT_0}{dz} \right)\]これを(8)式に代入すると
\[\begin{align} N^2 &= -g \left\{ -\frac{1}{T_0} \left( g \frac{\mu m_p}{k_B} + \frac{dT_0}{dz} \right) + \frac{g}{C_s^2} \right\} = \frac{g}{T_0} \left( g \frac{\mu m_p}{k_B} + \frac{dT_0}{dz} - \frac{gT_0}{C_s^2} \right) \notag \\ &= \frac{g}{T_0} \left( g \frac{\rho_0 T_0}{P_0} + \frac{dT_0}{dz} - \frac{gT_0}{C_s^2} \right) = \frac{g}{T_0} \left\{ \frac{dT_0}{dz} - (\gamma -1) \frac{gT_0}{C_s^2} \right\} \tag{9} \end{align}\]ここで断熱のとき、温度が
\[P_0 = \frac{\rho_0}{\mu m_p} k_B T_0 = K \rho_0^\gamma \ \Longrightarrow \ T_0 = \frac{\mu m_p}{k_B} \frac{P_0}{\rho_0} = \frac{\mu m_p}{k_B} P_0 \frac{K^{1/\gamma}}{P_0^{1/\gamma}} = \frac{\mu m_p}{k_B} K^{1/\gamma} P_0^{\frac{\gamma-1}{\gamma}}\]のように書けるので、断熱を維持したときの\(z\)微分が
\[\left( \frac{dT_0}{dz}\right)_\mathrm{ad} = \frac{\mu m_p}{k_B} K^{1/\gamma} \frac{\gamma - 1}{\gamma} \frac{dP_0}{dz} P_0^{-1/\gamma} = \frac{\mu m_p}{k_B} \frac{1}{\rho_0} \frac{\gamma - 1}{\gamma} \frac{dP_0}{dz} \underbrace{=}_{(1)} - \frac{\mu m_p}{k_B} \frac{\gamma-1}{\gamma} g\]となります。さらに\(C_s^2 = \gamma P_0 / \rho_0 = \gamma k_B T_0 / (\mu m_p)\)より
\[\left( \frac{dT_0}{dz}\right)_\mathrm{ad} = - (\gamma-1) \frac{g T_0}{C_s^2} \tag{10}\]です。(9), (10)式より
\[N^2 = \frac{g}{T_0} \left\{ \frac{dT_0}{dz} - \left( \frac{dT_0}{dz}\right)_\mathrm{ad}\right\} \tag{11}\]と書き直すことができます。(6)式から、ここまで流体に働く浮力を計算していたので、これを元に流体要素に対して運動方程式を立てることができます。
\[\rho_0 \frac{D \delta z}{Dt} = - N^2 \rho_0 \delta z \tag{12}\](12)式は\(N^2>0\)のとき\(\omega = N\)の単振動を表す式です。逆に\(N^2 <0\)のとき、すなわち
\[- \frac{dT_0}{dz} > -\left( \frac{dT_0}{dz} \right)_\mathrm{ad} \tag{13}\]のように断熱での温度勾配よりも温度変化が激しいとき、流体は上昇・下降を続ける不安定な状態であることがわかります。(13)式をSchwarzschild criterionと呼びます。またこの不安定性を対流不安定性と呼びます。このようにして恒星内部の対流は駆動されていると考えられています。
エントロピーを用いた理解
これはエントロピーの議論から直感的に考えることができます。簡単のため、以下の議論では\(P= C \rho^\Gamma \ (\Gamma>1)\)で系の状態が記述され、考えている系は恒星のように\(z\)とともに温度\(T\)が減少していくような構造を持つとします。\(\Gamma = 1\)は等温構造、\(\Gamma = \gamma = 5/3\)は理想気体・断熱構造にそれぞれ対応しています。\(\rho, P\)を温度で表現すると
\[P = \frac{\rho}{\mu m_p} k_B T = C\rho^\Gamma \ \Longrightarrow \ \rho = C_1 T^{\frac{1}{\Gamma-1}}, \quad P = C_2 T^{\frac{\Gamma}{\Gamma-1}}\]のようになるので、エントロピーは
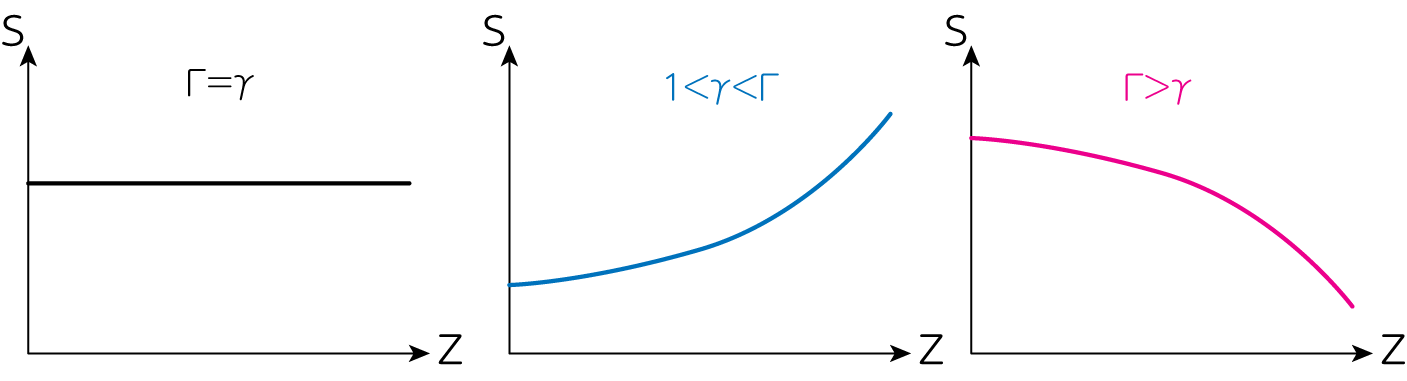
\[s = C_V \ln \frac{P}{\rho^\gamma} \propto \ln T^{\frac{\Gamma-\gamma}{\Gamma-1}} = \frac{\Gamma-\gamma}{\Gamma-1} \ln T\]と書けます。今は\(z\)とともに\(T\)が減少するような系を考えているので、\(\ln T\)も同様に単調減少します。よってエントロピーの増減は\(\Gamma-\gamma\)の部分だけを考えれば、その挙動が判明します。系が断熱、すなわち\(\Gamma = \gamma\)であれば、当然ですがエントロピーは保存し\(z\)に依存しません(下図参照)。
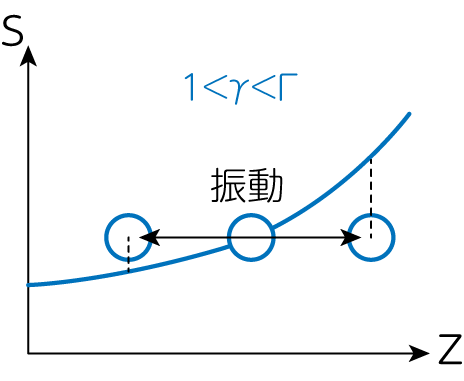
まずは\(1<\Gamma<\gamma\)の場合を考え、ここで断熱的に流体要素を\(+z\)方向に動かしましょう。すると周囲よりもエントロピーが低い(温度が低いことに対応)ため、収縮して重くなり、重力で元の位置に戻ります。逆に\(-z\)方向に動かした時も、周囲よりエントロピーが高い(温度が高いことに対応)ため、膨張して軽くなり、浮力で元の位置に戻されます。以上から、この場合は安定に振動を続けます。
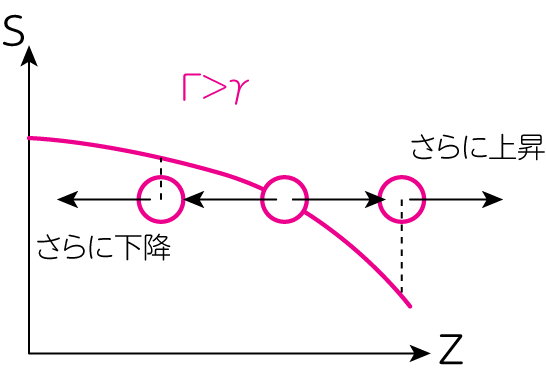
次に\(\Gamma>\gamma\)を考えます。同様に断熱的に流体要素を\(+z\)方向に動かすと、周囲よりもエントロピーが高い(温度が高いことに対応)ことがわかります。するとさらに膨張して軽くなり余計に浮力が働き、上昇を続けます。逆に断熱的に流体要素を\(-z\)方向に動かすと、周囲よりもエントロピーが低い(温度が低いことに対応)ことがわかります。するとさらに収縮して重くなり、重力によって下降を続けることになります。以上から、この場合は不安定です。
定量的な導出
それでは定量的に分散関係式を導いてみましょう。磁場や回転などがある場合を含めた一般的な式より
\[\omega^2 \mathbf{v}_1 = C_s^2 \mathbf{k} (\mathbf{k} \cdot \mathbf{v}_1) + i (\gamma-1) g (\mathbf{k} \cdot \mathbf{v}_1) \mathbf{e}_z + i g v_{1z} \mathbf{k} - 2i \omega \boldsymbol{\Omega} \times \mathbf{v}_1 + \frac{1}{4\pi \rho_0} [\mathbf{k} \times \{\mathbf{k} \times (\mathbf{v}_1 \times \mathbf{B}_0)\}] \times \mathbf{B}_0 \tag{14}\]ここで\(\mathbf{B}_0 = \boldsymbol{\Omega} = \mathbf{0}\)とします。(14)式において両辺\(\mathbf{k}\)との内積をとったものを考えると
\[\begin{align} &\omega^2 (\mathbf{v}_1 \cdot \mathbf{k}) = C_s^2 k^2 (\mathbf{k} \cdot \mathbf{v}_1) + i (\gamma-1) g (\mathbf{k} \cdot \mathbf{v}_1) k_z + ig k^2 v_{1z} \notag \\ &\Longrightarrow \ i g k^2 v_{1z} = (\mathbf{k} \cdot \mathbf{v}_1) \{ \omega^2 - C_s^2 k^2 - i(\gamma-1) g k_z\} \tag{15} \end{align}\]そして(14)式において両辺\(\mathbf{e}_z\)との内積をとったものを考えると
\[\omega^2 v_{1z} = C_s^2 k_z (\mathbf{k} \cdot \mathbf{v}_1) + i (\gamma-1)g (\mathbf{k} \cdot \mathbf{v}_1) + i g k_z v_{1z} \ \Longrightarrow \ (\omega^2 -i g k_z) v_{1z} = (\mathbf{k} \cdot \mathbf{v}_1) \{ C_s^2 k_z + i (\gamma-1) g\} \tag{16}\](15), (16)式を用いて\((\mathbf{k} \cdot \mathbf{v}_1)/v_{1z}\)を消去すると
\[igk^2 \{ C_s^2 k_z + i(\gamma-1) g\} = (\omega^2 - igk_z) \{ \omega^2 - C_s^2 k^2 - i(\gamma-1) gk_z\} \tag{17}\]ここまで圧縮による効果(すなわち音波の項)を残して変形してきましたが、今は重力で伝播していく波を考えます。すなわち(8), (11)式のBrunt-Väisälä周波数程度の波を導出しようと考えており、これは音波に比べて十分小さい周波数であることが知られています。よって調べるのは、波長がscale-heightよりも十分短いものに限るとします。言い換えると、局所解析(local analysis)として
\[\lambda = \frac{2\pi }{k} \ll \frac{C_s^2}{g} \simeq \Lambda \ \Longrightarrow \ \omega \simeq \frac{g}{C_s} \ll k C_s\]を仮定します。(17)式の両辺を\(k^2 C_s^2\)で割ると
\[\begin{aligned} &ig \left\{ k_z + i (\gamma-1) \frac{g}{C_s^2} \right\} = (\omega^2 - i g k_z) \left\{ \frac{\omega^2}{k^2 C_s^2} -1 - i(\gamma-1) \frac{g}{C_s^2} \frac{k_z}{k^2} \right\} \simeq - (\omega^2 - i gk_z) \left\{ 1 + i (\gamma-1) \frac{g}{C_s^2} \frac{k_z}{k^2}\right\} \\ &\Longrightarrow \ i g k_z - (\gamma-1) \frac{g^2}{C_s^2} \simeq - \omega^2 \left\{ 1 + i (\gamma-1) \frac{g}{C_s^2} \frac{k_z}{k^2}\right\} + igk_z - (\gamma-1) \frac{g^2}{C_s^2} \frac{k_z^2}{k^2} \end{aligned}\]よって分散関係式が
\[\omega^2 = (\gamma-1) \frac{g^2}{C_s^2} \left( 1- \frac{k_z^2}{k^2}\right) \tag{18}\]と求まります。\(k_z = k \cos \theta_g\) (\(\theta_g\)は波数ベクトル\(\mathbf{k}\)と重力の成す角度)と置くと
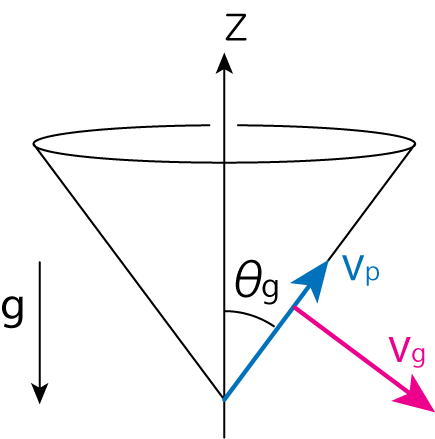
\[\omega^2 = \underbrace{(\gamma-1) \frac{g^2}{C_s^2}}_{\equiv N^2} \sin^2 \theta_g \ \Longrightarrow \ \omega = N \sin \theta_g \tag{19}\]この分散関係式を満たす波動を内部重力波(internal gravity waves)と呼びます。分散関係式を見てわかるように、\(\theta_g =0, \pi\)のとき、すなわち重力に平行な方向には内部重力波は伝播しません。鉛直下向きの重力に対して上向きに\(\theta_g\)方向に内部重力波が伝播していくとき、その伝播の仕方は角度\(\theta_g\)の円錐状となります。そのときの位相速度は
\[v_p = \frac{\omega}{k} = \frac{N}{k} \sin \theta_g \tag{20}\]となり、群速度は
\[\begin{align} \mathbf{v}_g &=\frac{\partial \omega}{\partial \mathbf{k}} = N \frac{\partial }{\partial k_i} \left( 1-\frac{k_z^2}{k_j k_j}\right)^{1/2} \mathbf{e}_i = \frac{N}{2} \left( 1 - \frac{k_z^2}{k_j k_j}\right)^{-1/2} \left( -\frac{2 k_z \delta_{iz} k_j k_j - k_z^2 2 k_j \delta_{ij}}{(k_j k_j)^2}\right) \mathbf{e}_i \notag \\ &= \frac{N}{2} \left( 1- \frac{k_z^2}{k^2} \right) \left( \begin{array}{c} \frac{2k_x k_z^2}{k^4} \\ \frac{2k_y k_z^2}{k^4} \\ -2\frac{k_x^2 + k_y^2}{k^4} k_z \end{array} \right) = \frac{N}{\sin \theta_g} \left( \begin{array}{c} \frac{k_x k_z^2}{k^4} \\ \frac{k_y k_z^2}{k^4} \\ -\frac{\sin^2 \theta_g}{k^2} k_z \end{array} \right) \tag{21} \end{align}\]となります。\(z\)成分だけ取り出してきても\(v_{gz} = - \omega k_z/k^2\)となることからもわかるように、波としては上向きに伝播していくにもかかわらず、エネルギーの流れは反対に下向きであることがわかります。ちなみに(21)式から\(\mathbf{k} \cdot \mathbf{v}_g = 0\)であることから、内部重力波の伝播コーンに垂直な方向にエネルギーが流れることがわかります。
参考文献
[1] Priest, “Solar Magnetohydrodynamics”
[2] 観山正見, 野本憲一, 二間瀬敏史, “天体物理学の基礎 II”
[3] 福江純, 和田圭一, 梅村雅之, “宇宙流体力学の基礎”