ラゲール多項式
ラゲールの微分方程式の解となる多項式です。エドモン・ニコラス・ラゲールというフランスの数学者が考えました。この微分方程式・多項式は、量子力学で目にする方が多いかもしれません。水素原子の周りの電子の半径方向の確率分を表現するのに用いられます。
母関数定義
母関数展開
\[\frac{e^{-zt/(1-t)}}{1-t} = \sum_{n=0}^\infty \frac{L_n(z)}{n!} t^n \tag{1}\]によって定義される\(L_n (z)\)をラゲール多項式と呼びます。
漸化式
\[\begin{aligned} &(1) \ \underbrace{\Longrightarrow}_{z微分} \ \sum_{n=0}^\infty \frac{t^n}{n!} \frac{dL_n}{dz} = \frac{1}{1-t} \left( - \frac{t}{1-t}\right) e^{-zt/(1-t)} = - \frac{t}{1-t} \sum_{n=0}^\infty \frac{L_n}{n!} t^n \\ &\underbrace{\Longrightarrow}_{\times (1-t)} \ \sum_{n=0}^\infty \frac{t^n}{n!} \frac{dL_n}{dz} - \sum_{n=0}^\infty \frac{t^{n+1}}{n!} \frac{dL_n}{dz} = - \sum_{n=0}^\infty \frac{t^{n+1}}{n!} L_n \ \Longrightarrow \ \sum_{n=0}^\infty \frac{t^n}{n!} \frac{dL_n}{dz} = \sum_{n=1}^\infty \frac{t^n}{(n-1)!} \left( \frac{dL_{n-1}}{dz} -L_{n-1}\right) \end{aligned}\]よって、\(t^n\)の係数を比較すると
\[\frac{dL_n}{dz} = n\frac{dL_{n-1}}{dz} -n L_{n-1} \ (n \geq 1) \tag{2}\] \[\begin{aligned} &(1) \ \underbrace{\Longrightarrow}_{t微分} \ \sum_{n=1}^\infty \frac{L_n}{(n-1)!} t^{n-1} = \frac{1}{(1-t)^2} e^{-zt/(1-t)} - \frac{z}{(1-t)^3} e^{-zt/(1-t)} = \frac{1}{1-t} \sum_{n=0}^\infty \frac{L_n}{n!} t^n - \frac{z}{(1-t)^2} \sum_{n=0}^\infty \frac{L_n}{n!} t^n \\ &\underbrace{\Longrightarrow}_{\times (1-t)^2} \ (1-2t-t^2) \sum_{n=1}^\infty \frac{L_n}{(n-1)!} t^{n-1} = (1-t) \sum_{n=0}^\infty \frac{L_n}{n!} t^n - z \sum_{n=0}^\infty \frac{L_n}{n!} t^n \\ &\Longrightarrow \ \sum_{n=1}^\infty \frac{L_n}{(n-1)!} t^{n-1} - 2 \sum_{n=1}^\infty \frac{L_n}{(n-1)!}t^n + \sum_{n=1}^\infty \frac{L_n}{(n-1)!} t^{n+1} = \sum_{n=0}^\infty \frac{L_n}{n!} t^n - \sum_{n=0}^\infty \frac{L_n}{n!} t^{n+1} - z \sum_{n=0}^\infty \frac{L_n}{n!} t^n \\ &\Longrightarrow \ \sum_{n=0}^\infty \frac{L_{n+1}}{n!} t^n - 2 \sum_{n=1}^\infty \frac{L_n}{(n-1)!} t^n + \sum_{n=2}^\infty \frac{L_{n-1}}{(n-2)!} t^n = \sum_{n=0}^\infty \frac{L_n}{n!} t^n - \sum_{n=1}^\infty \frac{L_{n-1}}{(n-1)!} t^n -z \sum_{n=0}^\infty \frac{L_n}{n!} t^n \end{aligned}\]よって、\(t^n\)の係数を比較すると
\[L_{n+1} -2n L_n + n(n-1) L_{n-1} = L_n - n L_{n-1} -zL_n \ \Longrightarrow \ L_{n+1} - (2n+1-z) L_n + n^2 L_{n-1} = 0 \ (n \geq 2) \tag{3}\] \[(2) \times n \ \Longrightarrow \ n\frac{dL_n}{dz} = n^2 \frac{dL_{n-1}}{dz} -n^2 L_{n-1}\] \[(2) \ \underbrace{\Longrightarrow}_{n\rightarrow n+1} \ \frac{dL_{n+1}}{dz} = (n+1) \frac{dL_n}{dz} -(n+1) L_n\] \[(3) \ \underbrace{\Longrightarrow}_{z微分} \ \frac{dL_{n+1}}{dz} - (2n+1-z) \frac{dL_n}{dz} + L_n + n^2 \frac{dL_{n-1}}{dz} = 0\]これらより
\[(n+1) \frac{dL_n}{dz} - (n+1) L_n - (2n+1-z) \frac{dL_n}{dz} + L_n + n \frac{dL_n}{dz} + n^2 L_{n-1} = z\frac{dL_n}{dz} - nL_n + n^2 L_{n-1} = 0 \tag{4}\](2), (3), (4)がラゲール多項式が満たす漸化式です。
ラゲールの微分方程式
\[\begin{aligned} &(4) \ \underbrace{\Longrightarrow}_{z微分} \ \frac{dL_n}{dz} + z \frac{d^2L_n}{dz^2} -n \frac{dL_n}{dz} + n \underbrace{n\frac{dL_{n-1}}{dz}}_{(2)} = \frac{dL_n}{dz} + z\frac{d^2 L_n}{dz^2} -n\frac{dL_n}{dz} + n\frac{dL_n}{dz} + \underbrace{n^2 L_{n-1}}_{(4)} \\ &= \frac{dL_n}{dz} + z\frac{d^2 L_n}{dz^2} + nL_n -z \frac{dL_n}{dz} = 0 \end{aligned}\] \[\therefore \ z \frac{d^2 L_n}{dz^2} + (1-z) \frac{dL_n}{dz} + nL_n = 0 \tag{5}\]これを(5)式をラゲールの微分方程式と呼びます。
具体的な形
次にラゲール多項式の具体的な形を導きましょう。
\[(1) \ \Longrightarrow \ \sum_{n=0}^\infty \frac{L_n}{n!} t^n = \frac{1}{1-t} e^{-zt/(1-t)} \underbrace{=}_{テイラー展開} \frac{1}{1-t} \sum_{m=0}^\infty \frac{1}{m!} \left( -\frac{zt}{1-t}\right)^m = \sum_{m=0}^\infty \frac{(-1)^m}{m!} z^m \frac{t^m}{(1-t)^{m+1}}\]ここで
\[\frac{1}{(1-t)^m} = 1+(m+1) t + \frac{1}{2!} (m+1) (m+2) t^2 + \cdots + \frac{1}{r!} (m+1)(m+2) \cdots (m+r) t^r + \cdots = \sum_{r=0}^\infty \frac{(m+r)!}{r! m!} t^r\]より
\[\begin{align} \sum_{n=0}^\infty \frac{L_n}{n!} t^n &= \sum_{m=0}^\infty \frac{(-1)^m}{m!} z^m t^m \sum_{r=0}^\infty \frac{(m+r)!}{r! m!} t^r = \sum_{m=0}^\infty \sum_{r=0}^\infty \frac{(-1)^m (m+r)!}{r! (m!)^2} z^m t^{m+r} \notag \\ & \underbrace{=}_{m+r=n} \sum_{n=0}^\infty \sum_{m=0}^n \frac{(-1)^m n!}{(n-m)! (m!)^2} z^m t^n \tag{6} \end{align}\]\(z\)による級数展開表現(6)式と次の微分表現が一致することを示してみましょう。
\[\begin{aligned} e^z \frac{d^n}{dz^n} (z^n e^{-z}) &= e^z \sum_{m=0}^n {}_n C_{n-m} n(n-1) \cdots (n-(n-m-1)) (-1)^m e^{-z} = \sum_{m=0}^n \frac{(-1)^m n!}{m! (n-m)!} n (n-1) \cdots (m+1) z^m \\ &= \sum_{m=0}^n \frac{(-1)^m (n!)^2}{(m!)^2 (n-m)!} z^m = (6) \end{aligned}\] \[\therefore \ L_n (z) = e^z \frac{d^n}{dz^n} (z^n e^{-z})\]のように表現することもできます。
例
ラゲール多項式の具体例は以下のようなものです。
\[L_0 = 1\] \[L_1 = -z+1\] \[L_2 = z^2 - 4z + 2\] \[L_3 = -z^3 + 9z^2 -18z + 6\] \[L_4 = z^4 - 16z^3 + 72 z^2 -96z+24\]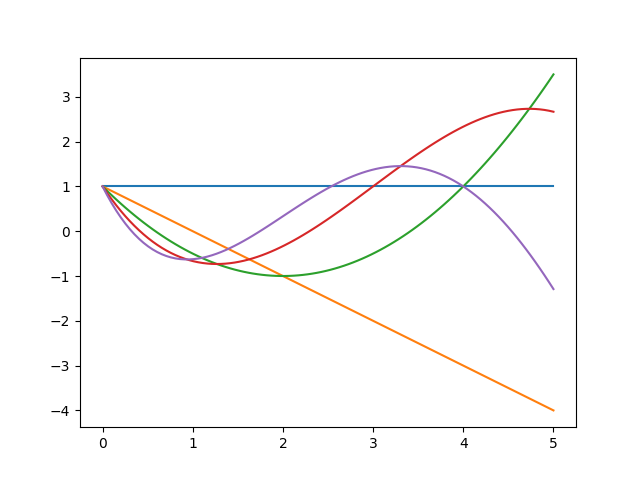
上図を作成するためのPythonスクリプトを以下に示します。
#!/usr/bin/env python3
from numpy.polynomial import Laguerre
import numpy as np
import matplotlib.pyplot as plt
if __name__ == '__main__':
# set variables
ix = 100
xmin = 0.0
xmax = 5.0
nmin = 0
nmax = 5
# set x coordinate
x = np.linspace(xmin, xmax, ix)
# main loop of plotting Laguerre polynomial
for n in range(nmin, nmax):
l = Laguerre.basis(n)(x)
plt.plot(x, l)
# make plot window
plt.show()
参考文献
- 改訂演習工科の数学4複素関数, 田島, 近藤
- 裳華房フィジックスライブラリー物理数学II, 中山
- 基礎物理学シリーズ3物理数学I, 福山, 小形