Table of contents
太陽についてのいくつかのこと
標準太陽モデル (standard solar models)
標準太陽モデルは、一般的な仮定のもとで元素組成が均一な状態から、太陽年齢 (\(\sim 46\)億年)だけ進化させることで得られます。 ここでいう一般的な仮定とは、元素組成均一の状態で形成された後は球対称が保たれる・輻射平衡領域ではガスの混合が起こらないなどがあります (最近の標準太陽モデルでは、輻射平衡領域での粒子拡散まで考慮することが多くなってきています。) 一般に星の明るさ\(L\)と半径\(R\)は、年齢\(t\)と元素組成\((X, Z)\)および表面対流層での混合距離と圧力変化距離との比\((\ell / H_p)\)の関数として表されています。 すなわち
\[L = L (X, Z, \ell / H_p, t), \quad R = R (X, Z, \ell / H_p, t)\]のように表すことができます。 したがって年齢\(t = 46\)億年で\(L = L_\odot, R = R_\odot\)であること、そしてスペクトル解析などから求められている太陽表面での重元素と水素の質量含有量比 \(Z / X \sim 0.0276\)の値を用いると、標準太陽モデルの\(X, Z, \ell / H_p\)が決定されます。 これらのパラメータ値は、モデル計算に用いられる不透明度テーブルや混合距離理論内の細かな仮定などに依存しますが、およそ\(X \sim 0.7, Z \sim 0.02, \ell / H_p \sim 1.5 - 2\)程度となります。
太陽光球 (photosphere)の温度 (有効温度; effective temperature)は5800K程度で、表面で観測される粒状斑からも太陽外層では対流が起こっていることがわかります。 対流層の深さは半径の30%程度で、そこに含まれる質量は2%程度です。 対流層の底では、温度が\(10^6\)K程度、密度は\(0.1 \mathrm{g / cm^3}\)程度とされています。 対流層のごく表面に近い、温度が数万K以下の場所では、温度勾配は\(\nabla_\mathrm{T} - \nabla_\mathrm{ad} \sim \mathcal{O}(1)\)ですが、深いところでは\(\nabla_\mathrm{T} \simeq \nabla_\mathrm{ad}\)の定エントロピー構造となっています。
光球のすぐ上空で温度が最低となり、それより上部の彩層 (chromosphere)では温度が上層ほど高くなります。 そのさらに上空では、高温 (\(\sim 2 \times 10^6\)K)でほぼ高温のコロナ(corona)が広がっています。
太陽の中心温度は\(1.56 \times 10^7\)Kで、密度は\(1.5 \times 10^2 \mathrm{g/cm^3}\)程度です。 水素からヘリウムの核融合反応(水素燃焼)によるエネルギー発生は、\(r \lesssim 0.2 R_\odot\)の中心付近だけで起こっています。 また太陽が生まれてから現在までに起こった水素燃焼により、中心での水素の質量含有量は最初の半分以下になっていると考えられています。
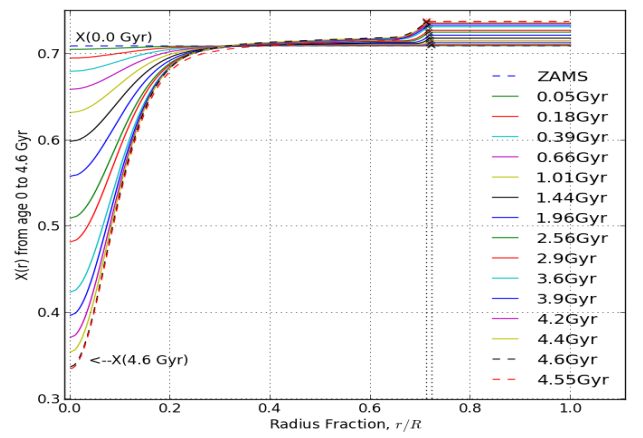
この図において\(r/R \sim 0.7\)あたりでグラフの折れ曲がりがあるのは、
太陽振動による太陽内部の構造の検証
太陽は、周期が約5分の振動をしていることがわかっています。 それは太陽面の各点の速度変化や輝度の変化により観測され、地上(GONG; Global Oscillation Network Group)および人工衛星(SOHO: SOlar and Heliospheric Observatory)での観測が行われてきました。 太陽振動は数千の固有振動モードの重ね合わせからなり、それらの周期と太陽面での波長を正確に測定することにより、太陽内部の構造を知ることができます。 このような学問分野を日震学 (Helioseismology)と呼び、急速に発展してきました。
次の図は、太陽表面の速度場の変動の様子を表したものです。 表示されている値が\(\sim 10 \mathrm{m/s}\)程度であることから、地球の地上の風くらいでそよいでいることがわかります。
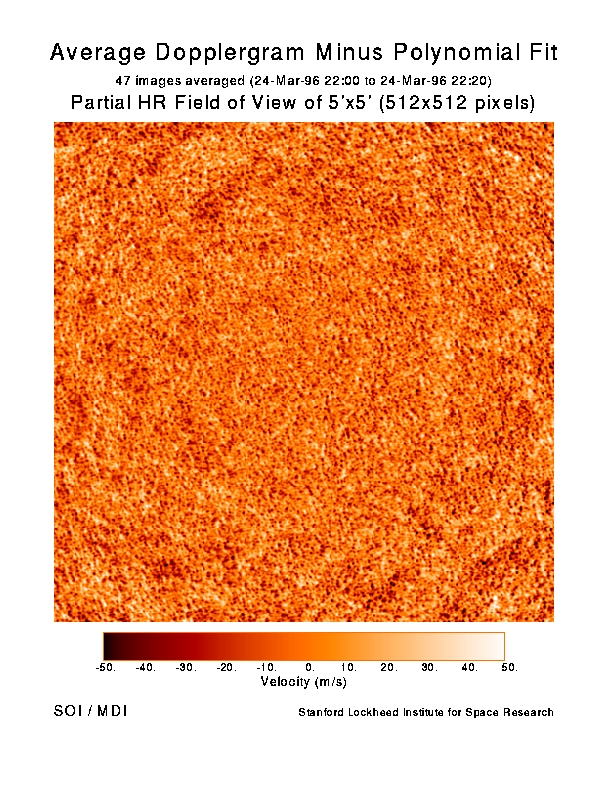
そして次の図は、上図を2次元のフーリエ分解\(v(\theta, \phi, t) = \sum w(\ell, \sigma) Y_\ell^m e^{i\sigma t}\)し、\(\ell \sigma\)平面を図示したものです。 \(n, \ell, m\)はそれぞれ、動径方向、天頂角方向、方位角方向の節の数(パターン分割数)を表します。 \(3\sim 4\)mHzの部分に濃い赤色があり、これは時間にして5分程度の振動に対応しています。 これを太陽の5分振動と呼ぶこともあります。

振動を球で表現した様子が以下になります。 これは例として、\(n=14, \ell=20, m = 16\)を描画したものです。 赤色と青色の部分は、流体要素が互いに反対方向に動く部分を表します。
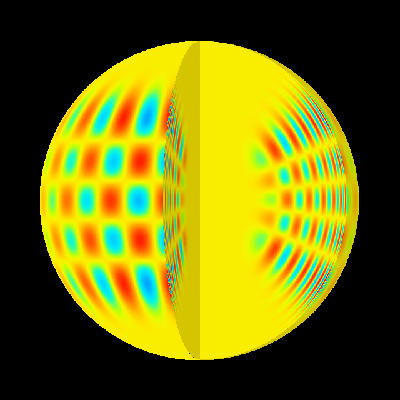
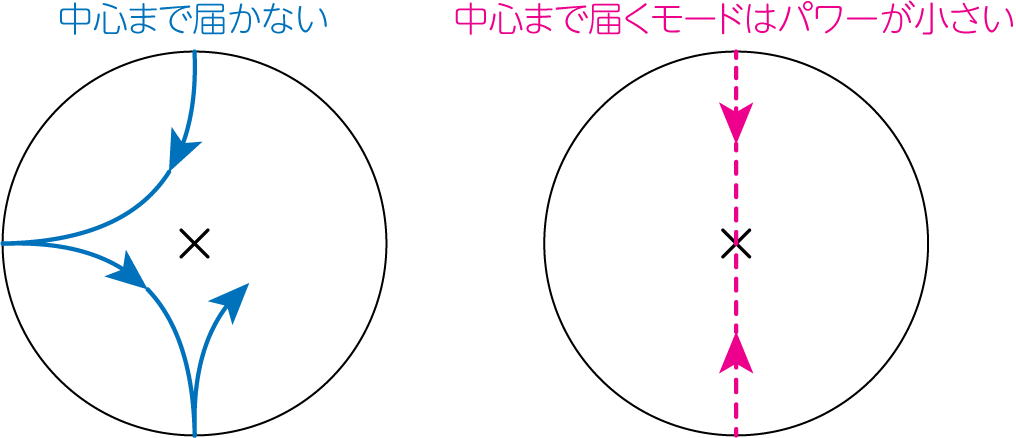
実際の太陽振動は、様々な波長・振動数の固有振動の重ね合わせとなっています。 日震学から求めた内部の音速(sun)と標準太陽モデル(model)から計算された音速との差を表したのが、次の図です。
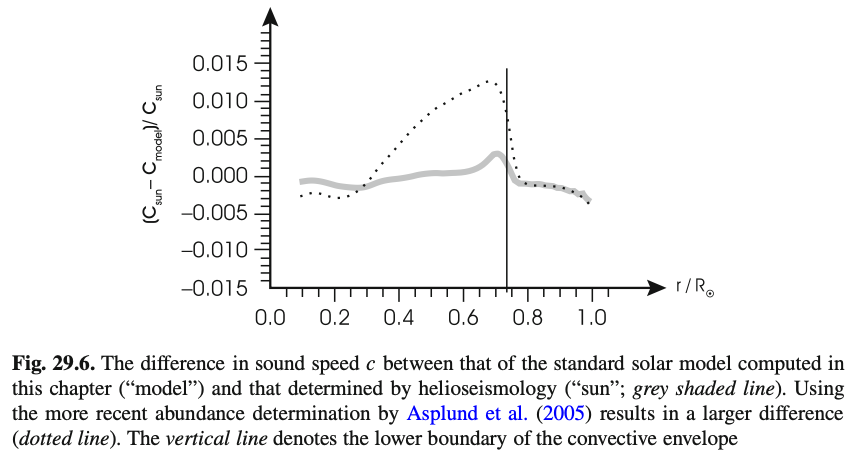
中心部で音速が求まっていないのは、中心まで伸びるモード数が少ないことからくる不確定要素が原因です。 また\(r / R_\odot \sim 1.0\)近傍でも音速の不確定性が大きく、これは静水圧平衡からのズレが大きいことが要因となっています。
太陽ニュートリノ (Solar neutrino)
水素燃焼で発生するエネルギーの多くはガンマ線として放出されますが、一部のエネルギーはニュートリノになります。 ガンマ線は発生するとすぐに周囲のガスにより吸収され、エネルギーの低い光子として再放出されます。 吸収と再放出を繰り返しながら、光は恒星内部を伝搬していきます。 そのため、中心で発生したガンマ線に起因する光子が、恒星表面に出てくるには数十万年の時間がかかります。 それに対し、ニュートリノは周囲のガスとほとんど相互作用を起こさないため、発生すると光速に近い速度で太陽内部を通り抜け、宇宙空間に飛び出していきます。 そのため、太陽からのニュートリノを観測することができると、現在の太陽の中心部の状態についての情報を得ることができます。
太陽で起こっている水素燃焼は主にppチェイン反応です。 次の図は、ppチェインの核反応と、その際に出るニュートリノの種々のエネルギーの大きさについて説明したものです。
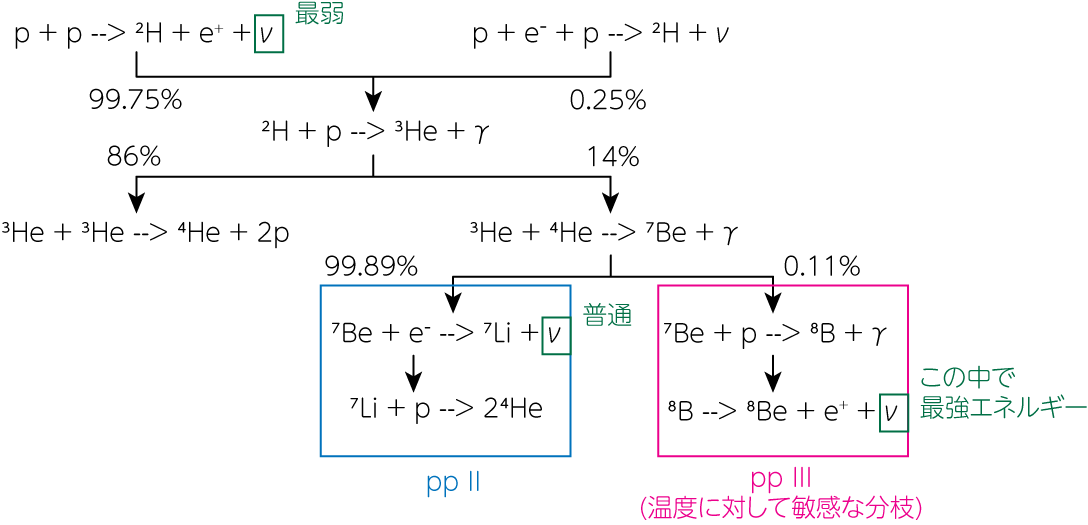
この中で\({}^8 \mathrm{B}\)の崩壊で出るニュートリノはBニュートリノと呼ばれ、10MeV程度の高いエネルギーまで流束を持ちます。 しかしpp反応のときに放出されるニュートリノ (ppニュートリノ)は0.4MeV以下の低いエネルギーを持ちます。 また\({}^7 \mathrm{Be}\)の電子捕獲反応に際して放出されるニュートリノは、2種類のエネルギーを持つのが特徴です。
ニュートリノは物質と相互作用をほとんど起こさないために、太陽中心の情報を持っているという利点があります。 逆を言えばそれらを観測するのは非常に困難で、巨大な装置が必要となります。
標準太陽モデルが予想するニュートリノフラックス
下表は、粒子拡散を無視した古典的な標準太陽モデル・粒子拡散を考慮した太陽モデル・粒子拡散を抑える効果のある弱い乱流を考慮した太陽モデル、から期待されるニュートリノ測定値を表しています。 各々のモデルで中心温度がわずかに異なるため、放出されるニュートリノの量も少しずつ異なっていることがわかります。
| パラメータ | 観測 | 拡散なし | 拡散 | 拡散と乱流 |
| Y Z (Z/X) | surface | 0.265 \(1.757 \times 10^{-2}\) 0.0245 conditions | 0.273 \(1.964 \times 10^{-2}\) 0.0277 \(\) | 0.296 \(1.89 \times 10^{-2}\) 0.0267 \(\) |
| Y Z (Z/X) \(\) | \(0.249 \pm 0.003\) \(0.0245 \times (1 \pm 0.1)\) transition | 0.265 \(1.7575 \times 10^{-2}\) 0.0245C radiation | 0.243 \(1.810 \times 10^{-2}\) 0.0245C convection | 0.247 \(1.79 \times 10^{-2}\) 0.0245C |
| \(R_\mathrm{conv} / R_\odot\) \(T_\mathrm{conv} \times 10^6\) (K) | \(0.713 \pm 0.003\) central | 0.729 2.055 conditions | 0.715 2.172 \(\) | 0.715 2.17 \(\) |
| \(Y_c\) \(Z_c\) \(T_c\times 10^6\) (K) \(\rho_c (\mathrm{g/cm^3})\) | Neutrino | 0.614 \(1.807 \times 10^{-2}\) 15.44 147.80 fluxes | 0.635 \(2.084 \times 10^{-2}\) 15.67 151.85 \(\) | 0.634 \(2.02 \times 10^{-2}\) 15.65 152 \(\) |
| \({}^{17} \mathrm{Cl}\) (SNU) contributors \({}^{71} \mathrm{Ga}\) (SNU) \(\) \({}^{71} \mathrm{Ga}\) (SNU) \(\) contributors \({}^8 \mathrm{B} (10^6 / \mathrm{cm^2/s})\) | \(2.55 \pm 0.25\) SNU pp: 0 pep: 0.225 \(76\pm 8\)SNU (cal=\(0.91 \pm 0.08\)) \(70 \pm 8\) SNU (cal=\(0.95 \pm 0.12\)) pp: 70.6 pep: 3.03 \(2.44 \pm 0.26\) | 5.65 \({}^7 \mathrm{Be}: 1.12, {}^8 \mathrm{B}: 5.49\) 119.4 \(\) 119.4 \(\) \({}^7 \mathrm{Be}: 34.17, {}^8 \mathrm{B}: 11.85\) 3.66 | 7.18 \({}^{13} \mathrm{N}: 0.077\) 127.2 \(\) 127.2 \(\) \({}^{13} \mathrm{N}: 2.88\) 4.82 | \(\approx 6.6-6.7\) \({}^{15} \mathrm{O}: 0.263 \ {}^{17} \mathrm{F}: 0.003\) \(\approx 142 - 125\) \(\) \(\approx 121 - 124\) \(\) \({}^{15} \mathrm{O}: 4.61, {}^{17} \mathrm{F}: 0.52\) \(\approx 4.6-4.7\) |
\({}^{37} \mathrm{Cl}による測定\)
太陽ニュートリノの最初の観測は、アメリカ合衆国のサウスダコタ州でR. Davis, Jr.行われました。 そこには615トン (40万リットル)の\(\mathrm{C_2 Cl_4}\)溶液 (洗剤の一種)を入れた巨大なタンクが、地下1500mに設置されました。
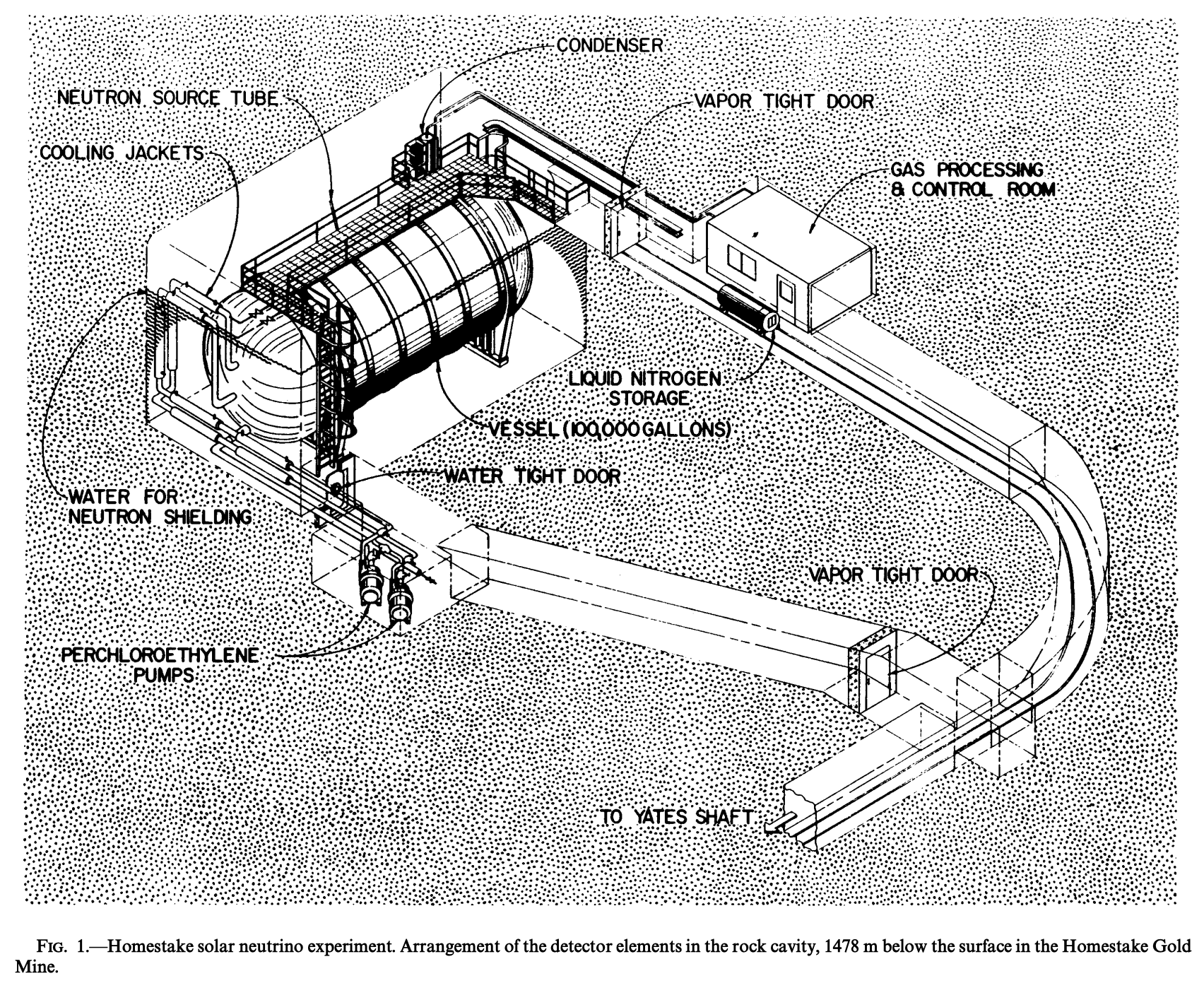
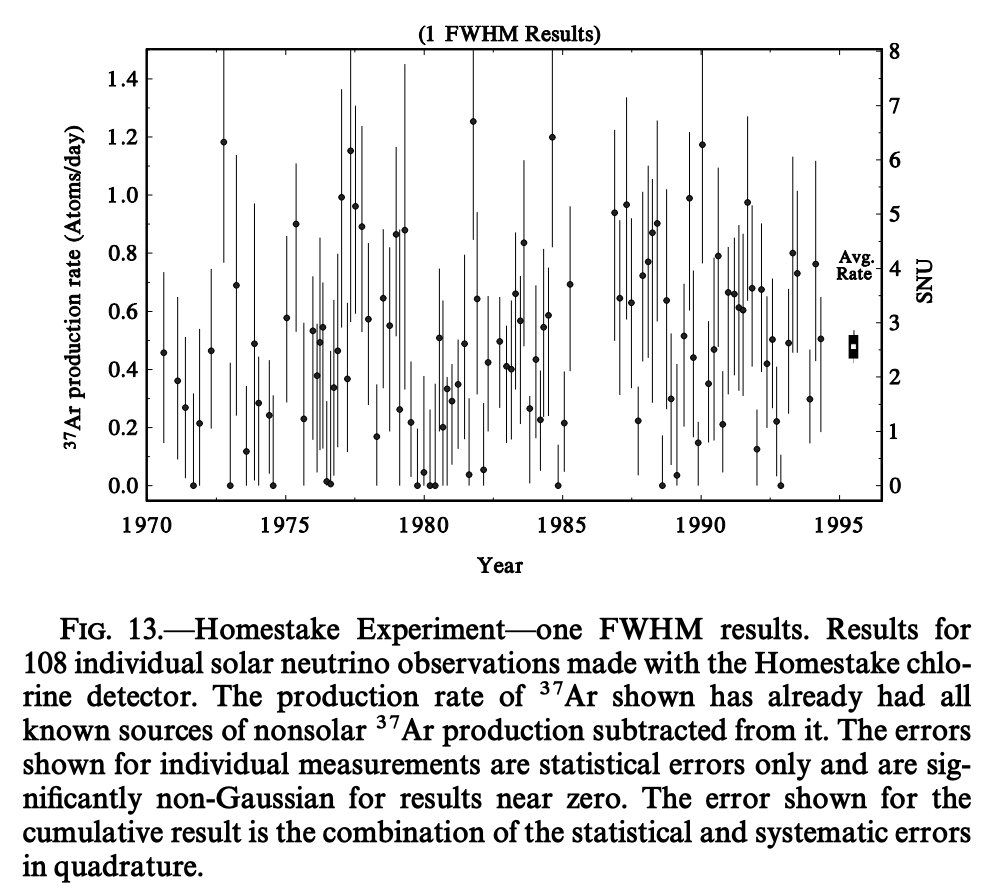
そこでは0.8MeV以上のエネルギーを持つニュートリノが、微小な確率で起こす
\[\nu + {}^{37} \mathrm{Cl} \ \longrightarrow \ \mathrm{e}^- + {}^{37} \mathrm{Ar} \quad (E_\nu > 0.814 \mathrm{MeV})\]の反応が利用されました。 ある期間タンクを放置したのち、その中で生成された\({}^{37} \mathrm{Ar}\)を集めます。 それらが半減期35日で電子を捕獲をし\({}^{37} \mathrm{Cl}\)に戻る際に放出される電子を検出することで、\({}^{37} \mathrm{Ar}\)の数を求めます。 タンクを1, 2ヶ月放置したのちに\({}^{37} \mathrm{Ar}\)の数を数えたところ、その数は20個程度でした。 このことからも、太陽ニュートリノの検出の難しさがわかります。
この装置による1970年から1995年までの太陽ニュートリノによる反応率の平均値は、\(2.56 \pm 0.16\) SNUでした。 ここで1SNU (Solar Neutrino Unit)は、1原子当たり毎秒起こるニュートリノによる反応 (この場合は\({}^{37} \mathrm{Ar}\)の生成)が\(10^{-36}\)回起こることを表します。 一方、標準太陽モデルから期待される値は7SNU程度で、観測値の3倍弱となっています。 この食い違いは、太陽ニュートリノ問題と呼ばれていました。
神岡での検出
Davis達の装置は、およそ20年間、太陽ニュートリノを検出する唯一の装置でした。 これに対し東京大学を中心とするグループが異なる方法によるニュートリノ検出装置を長野県神岡につくり、1987年から結果を出し始めました。 この装置はカミオカンデと呼ばれ、壁全体に光電子増倍管を並べたタンクに3000トンの水を入れたものです。
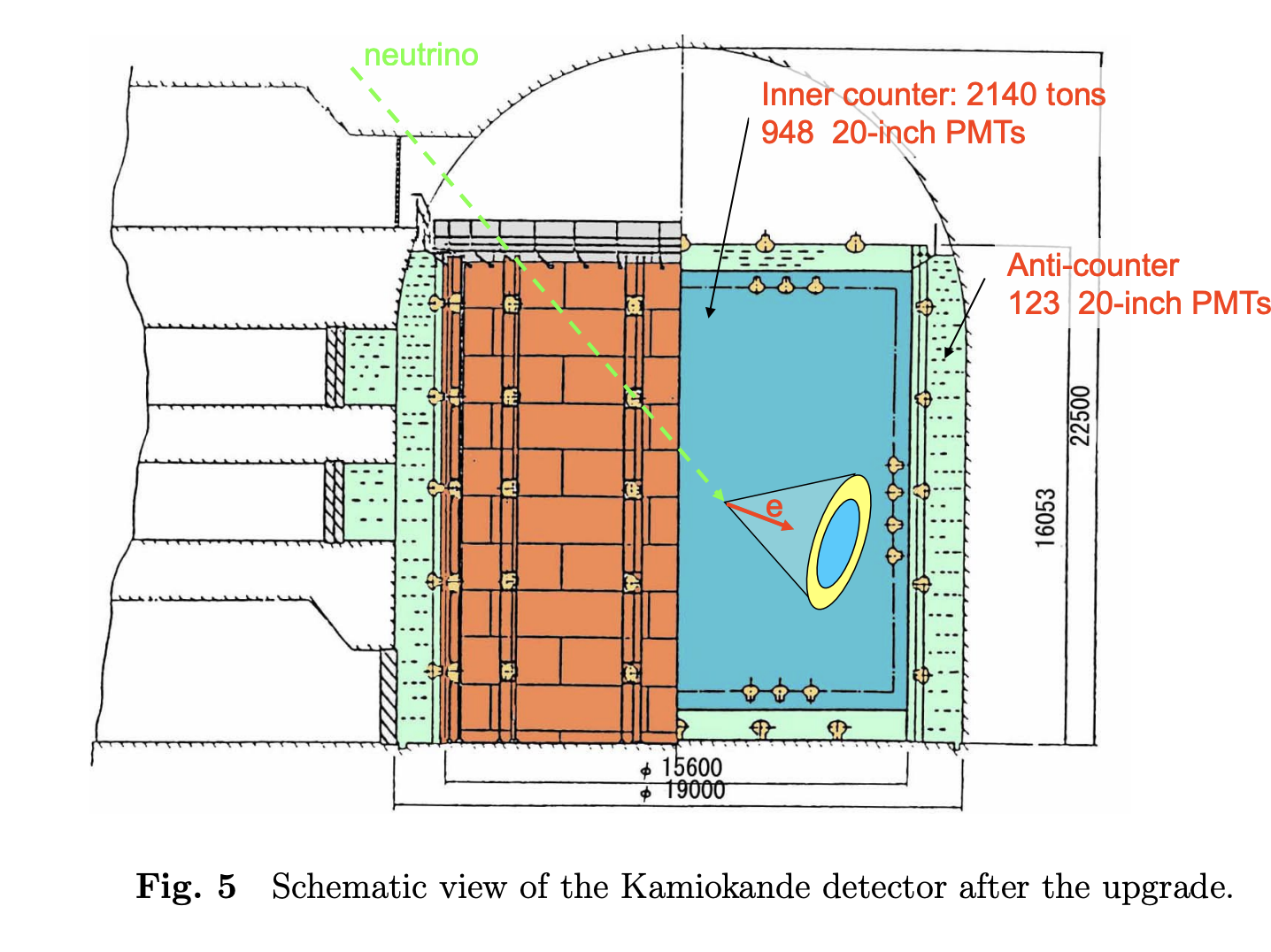
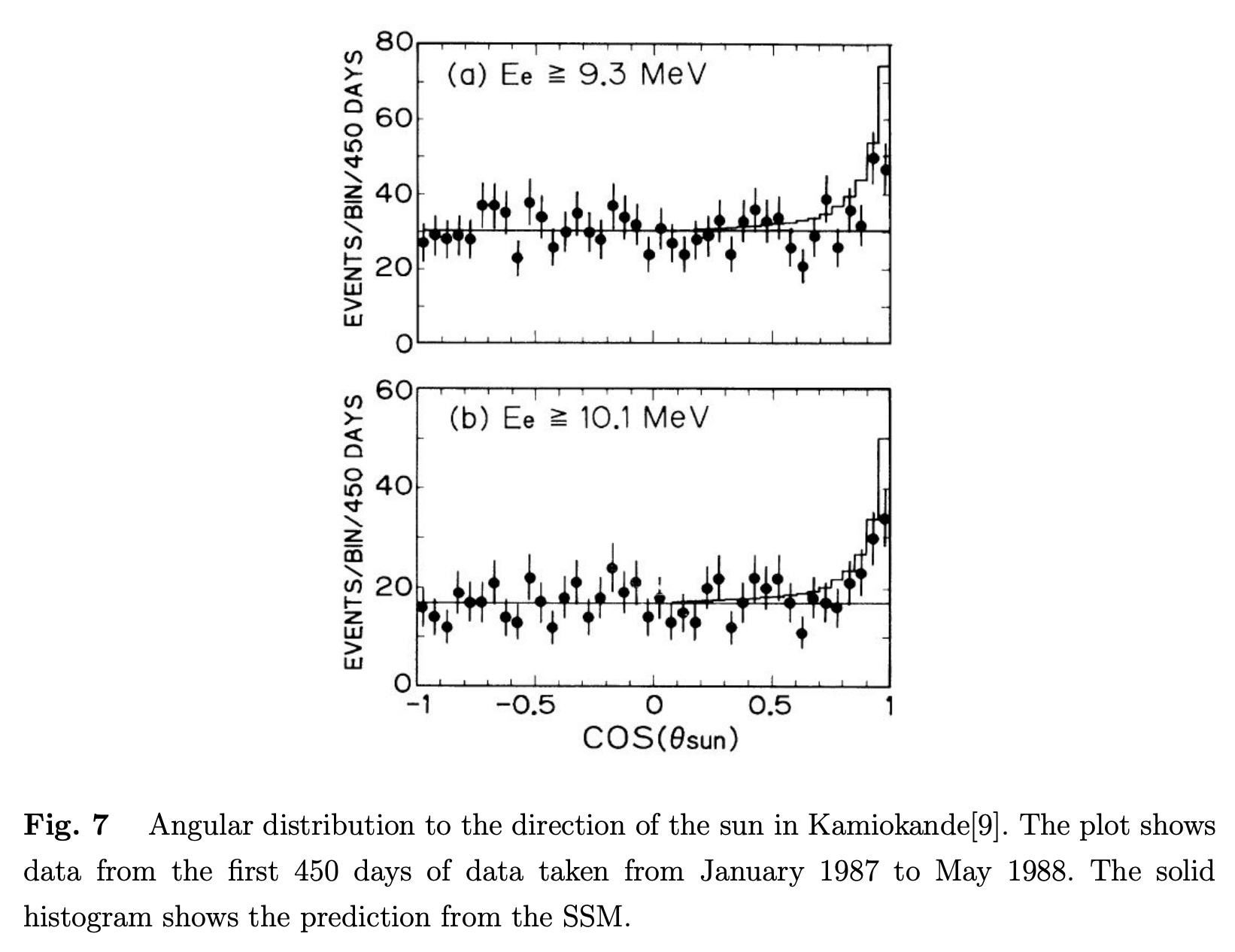
カミオカンデは1995年までデータを集積し、1996年からは容積を30倍のスーパーカミオカンデによってデータが取られています。
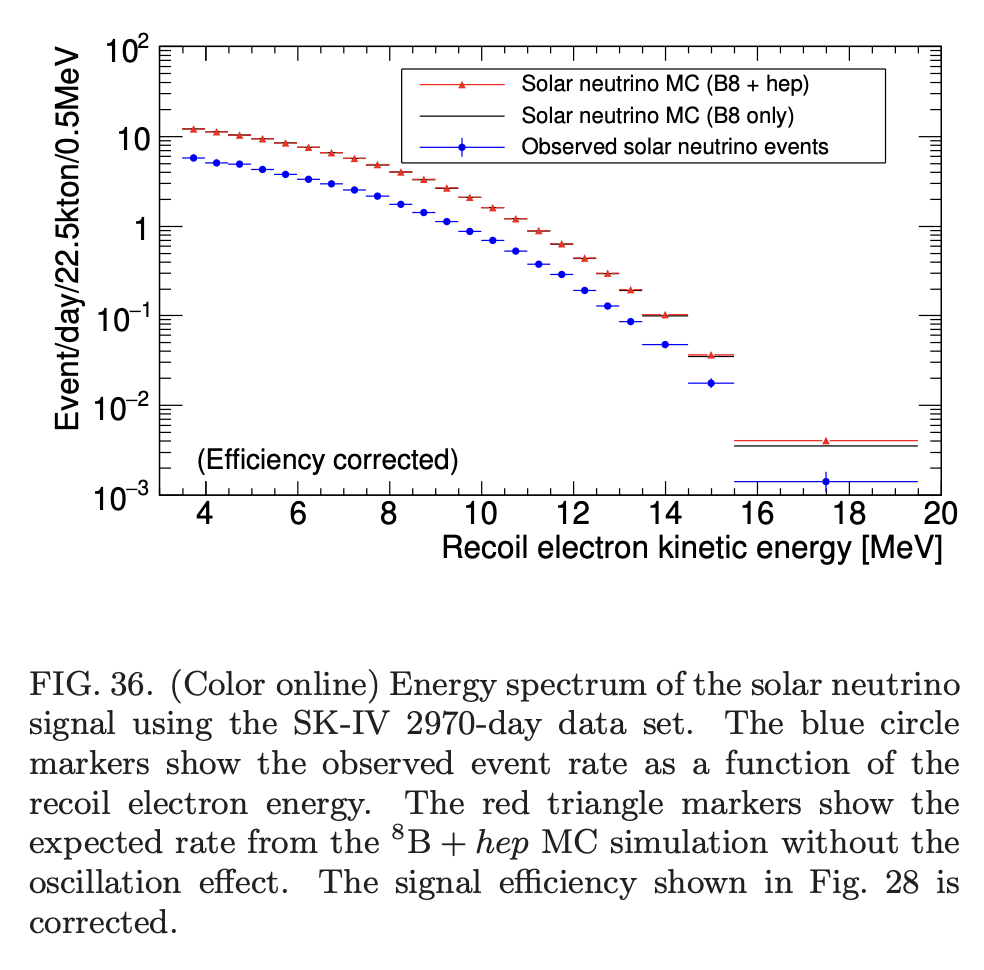
この装置では、タンク中でニュートリノが電子を跳ね飛ばし、電子が水中での光速度よりも速い速度を持ったときに出るチェレンコフ光を、壁に取り付けられた光電子増倍管が検出します。 エネルギー閾値は5MeV以上 (自然放射能による背景光によるもの)なので、\({}^8 \mathrm{B}\)の陽電子崩壊 \({}^8 \rightarrow \mathrm{Be}^\ast + \mathrm{e^+} + \nu_e\)から放出される、太陽からのニュートリノの中ではエネルギーの高い\({}^8 \mathrm{B}\)ニュートリノ (とhepニュートリノ\({}^3 \mathrm{He} + p \rightarrow {}^4 \mathrm{He} + e + \nu\))しか検出できません。 しかしこの装置は、ニュートリノの侵入方向とエネルギーが得られるという大きな利点を持っています (カミオカンデは1987年2月に大マゼラン雲に出現した超新星 1987Aの爆発時に放出されたニュートリノを検出したことでも有名です。) 1996年から稼働しているスーパーカミオカンデによるこれまでの観測結果の平均値は、\(2.32 \times 10^6 \mathrm{cm^{-2} s^{-1}}\)とされています。 これは標準太陽モデルから期待される値の、およそ半分であることを示しています。 また太陽周期の黒点数との相関は、あったとしてもとても弱いものであるという結果も得られています。
カミオカンデの結果は、\({}^{37} \mathrm{Cl}\)の結果の場合ほど大きな差ではありませんが、やはり標準太陽モデルとの食い違いを示しています。 ここから、太陽ニュートリノ問題が検出装置の問題ではないことが決定的に示されました。 しかし、これらの検出装置では、エネルギーは低いが豊富に出る ppニュートリノは検出できません。 上述の装置で最も重要なBニュートリノが出る反応は、太陽のエネルギー源としてはほとんど寄与せず、またその反応の起こる割合は温度に敏感です。
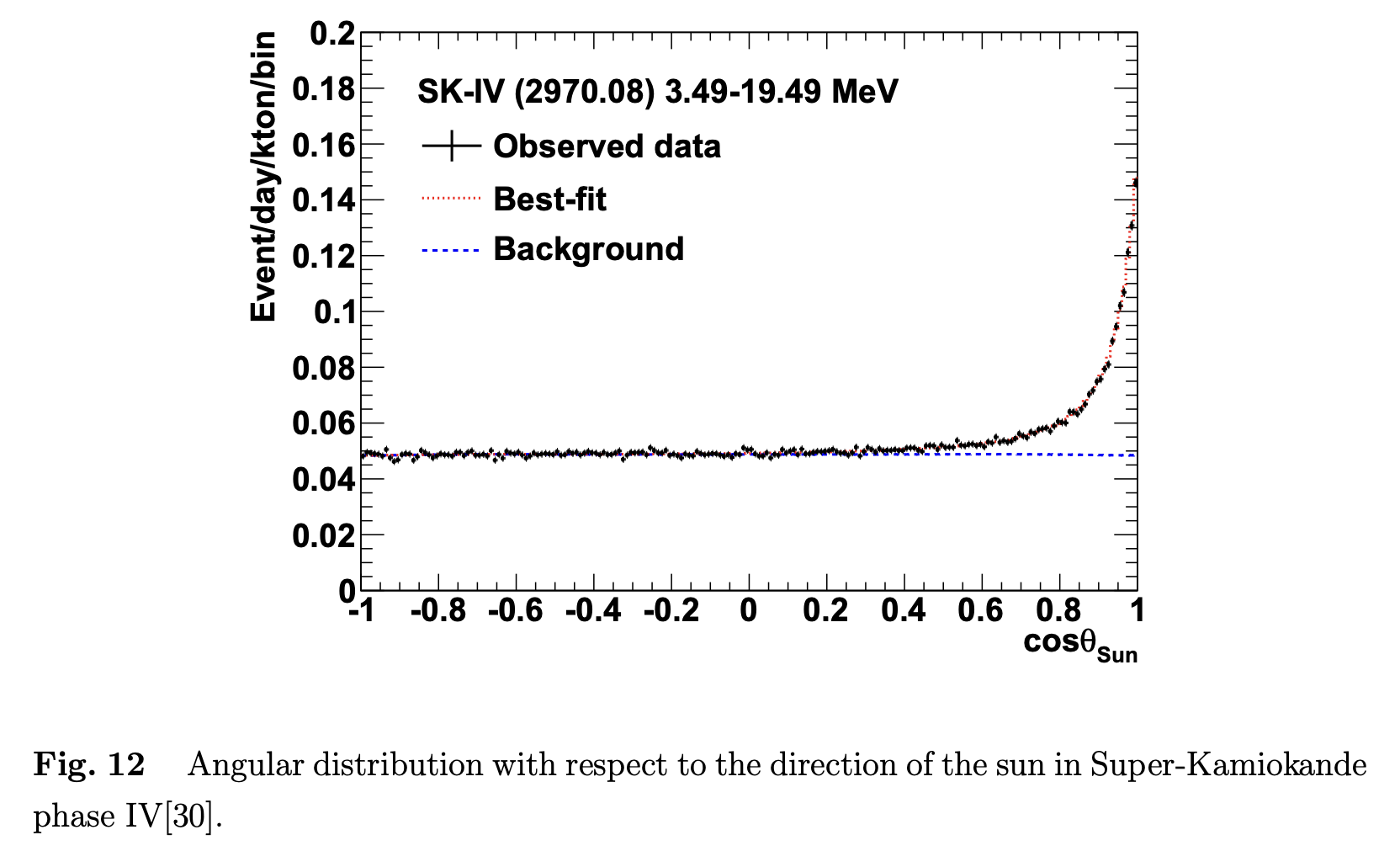
カミオカンデは小柴昌俊氏、スーパーカミオカンデは梶田隆章氏にそれぞれノーベル物理学賞をもたらしたことで有名です。
Gaを使った検出
ppニュートリノはエネルギーは低いものの、ppチェイン反応で水素燃焼が起こるときには必ず放出されるという特徴を持っています。 現在、GALLEX/GNO, SAGEという2つのグループにより、ppニュートリノを検出する装置が稼働しています。 GALLEX/GNOは30トンのGaを含む\(\mathrm{GaCl}_3\)水溶液を用いた装置で、イタリアのGran Sasso Underground Laboratoryで観測が行われています。 一方、SAGEは約50トンの金属ガリウム (融点29.8℃)を使用し、ロシアのコーカサス山地でロシア-アメリカ共同観測が行われています。
それらの検出では、ガリウムとニュートリノの反応 \(\nu + {}^{71} \mathrm{Ga} \rightarrow \mathrm{e}^- + {}^{71} \mathrm{Ge}\)が用いられています。 \({}^{71} \mathrm{Ge}\)が半減期11.4日で電子を捕獲して\({}^{71} \mathrm{Ga}\)に崩壊する際に出る放射線を捉えることで、生成されていた\({}^{71} \mathrm{Ge}\)の数を求めます。 \({}^{71} \mathrm{Ga}\)から\({}^{71} \mathrm{Ge}\)の生成は0.23MeV以上のエネルギーを持つニュートリノにより可能で、ppニュートリノの検出を可能にしています。 標準太陽モデルから期待される反応率は132SNUです。 このような理論的予想に対し、GALLEX/GNOとSAGEはともに70SNU程度で、いずれも標準太陽モデルからの期待値を下回っています。
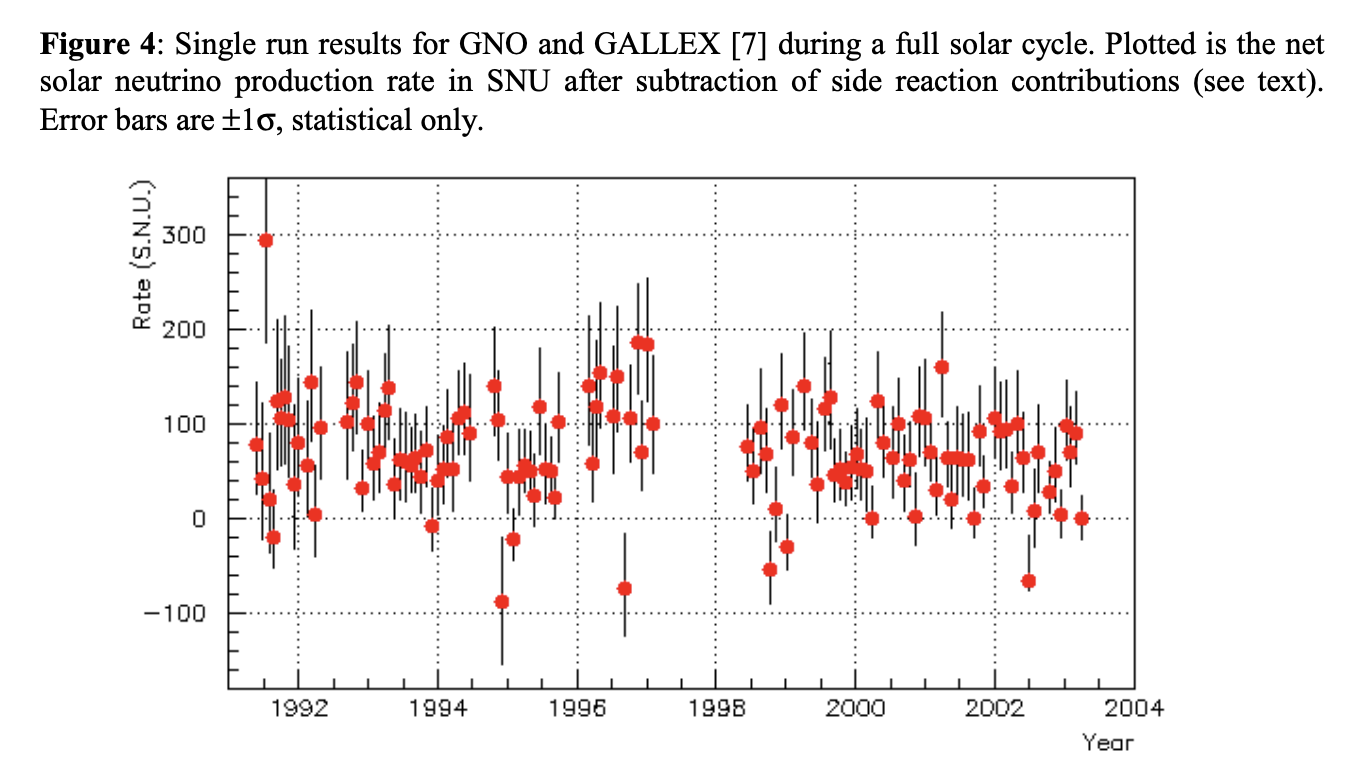
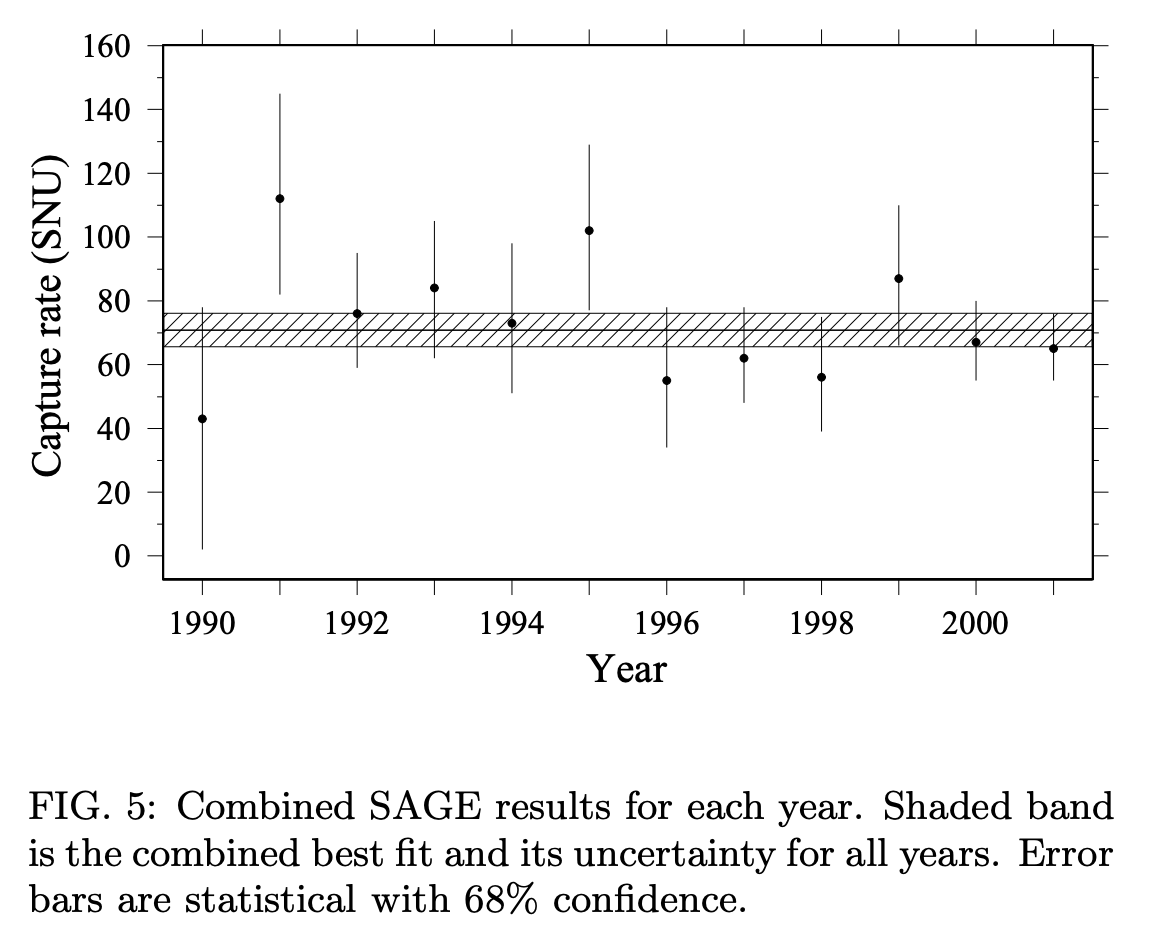
各装置による測定値の比較
pp-IIIチェインの反応が起こる率は温度に敏感なため、「カミオカンデの測定で予想値の半分しかニュートリノが来ていない」という結果に対し、すぐに思い浮かぶのは太陽モデルの中心温度を下げる補正です。 その補正は約5%程度下げれば良いですが、これでは逆に説明できない観測値が出てきます。
Clによる測定に対して予想される反応率は
| 種類 | pp | pep | \({}^7 \mathrm{Be}\) | \({}^8 \mathrm{B}\) | \({}^{13} \mathrm{N}\) | \({}^{15} \mathrm{O}\) | Total |
| 反応率(SNU) | 0 | 0.2 | 1.1 | 6.1 | 0.1 | 0.3 | 7.9 |
であるのに対し、測定結果は2.55SNUでした。 一方、\({}^8 \mathrm{B}\)ニュートリノだけに感度があるカミオカンデの測定では、理論的予想値の50%のフラックスを検出しました。 この結果から、\({}^8 \mathrm{B}\)ニュートリノにより、\(\mathrm{Cl}\)測定装置は理論値の半分の3SNUを受けているはずです。 ところが測定値が2.55SNUであることから、\({}^7 \mathrm{Be}\)ニュートリノの寄与が全くないことになります。
Gaによる測定に対して予想される反応率は
| 種類 | pp | pep | \({}^7 \mathrm{Be}\) | \({}^8 \mathrm{B}\) | \({}^{13} \mathrm{N}\) | \({}^{15} \mathrm{O}\) | Total |
| 反応率(SNU) | 70 | 3 | 34 | 12 | 4 | 6 | 129 |
であるのに対し、GALLEXとSAGEグループの平均実測値は約75SNUでした。 カミオカンデとスーパーカミオカンデの結果(\({}^8 \mathrm{B}\)ニュートリノの約50%を観測)を考慮すると、Gaによる測定では6SNUの\({}^8 \mathrm{B}\)ニュートリノの寄与を受けているはずです。 この\({}^8 \mathrm{B}\)ニュートリノの寄与を実測値から差し引くと、残りは69SNUとなります。 したがってpep, \({}^7 \mathrm{Be}, {}^{13} \mathrm{N}, {}^{15} \mathrm{O}\)からのニュートリノの寄与がゼロであったとすると、ppニュートリノに対してほぼ理論予想値の値が検出されたことになります。
したがって、3種類の測定装置による結果から
ということが言えます。 この測定結果を、太陽モデルの中心温度を変化させて実現させるのは困難です。 なぜなら\(F_\nu ({}^8 \mathrm{B})\)の方が\(F_\nu ({}^7 \mathrm{Be})\)よりも温度依存性が大きいため、温度を下げることで前者より大きく後者を大きく減少させることは不可能だからです。 中心温度が下がると、Bニュートリノフラックスの方がBeニュートリノフラックスよりも急激に下がるため、Beニュートリノフラックスだけを下げることはできません。 ppニュートリノフラックスは中心温度が下がると少し上昇するとされていますが、これは中心温度の減少によってpp-2, pp-3の反応率が下がるため、太陽光度を出すためにppチェイン反応の寄与が大きくなるためです。
素粒子物理学による解決
標準太陽モデルが予想するニュートリノフラックスよりも少ないニュートリノしか観測されないことに対する解決方法として、太陽で発生したニュートリノ (電子ニュートリノ)の一部が、これまでに使われた装置では観測されていないフレーバー(ミューまたはタウニュートリノ)に変化してしまったと考えることができます。 このニュートリノフレーバーの変化は、ニュートリノ振動と呼ばれます。 これには vacuum oscillations (真空振動?)と matter oscillations (物質振動?またの名をMSW効果)があります。 現在は、このMSW効果による説明がもっともらしいと考えられています。
Vacuum oscillations
ニュートリノが有限の質量を持ち、自由ニュートリノに対するハミルトニアンの固有状態が個々の質量状態に対応すると仮定しましょう。 このとき、電子・ミュー・タウニュートリノなどのフレーバー状態 (\(\vert \nu_e \rangle, \vert \nu_\mu \rangle, \vert \nu_\tau \rangle\))は質量状態 \(\vert \nu_j \rangle\)の重ね合わせ
\[\vert \nu_\alpha \rangle_t = \sum_{j=1}^3 U_{\alpha, j} e^{-i E_j t / \hbar} \vert \nu_j \rangle\]のように表されます。 ここで\(U\)は、個々の質量状態の寄与を表すユニタリ行列です。
以降、簡単のため、電子ニュートリノとミューニュートリノの間の振動のみを考えることにしましょう。 このとき\(U\)は
のように表現されます。 ここで\(\theta\)は vacuum mixing angle (真空混合角?)と呼ばれるものです。 よって、電子ニュートリノの時間変化は
\[\vert \nu_e \rangle_t = \cos \theta e^{-i E_1 t / \hbar} \vert \nu_1 \rangle + \sin \theta e^{-iE_2 t/ \hbar} \vert \nu_2 \rangle\]のようになります。 ここで\(E_1, E_2\)はそれぞれ、同じ運動量に対する2つの質量状態\(\vert \nu_1 \rangle, \vert \nu_2 \rangle\)のエネルギーを表します。 \(t = 0\)で電子ニュートリノだったニュートリノに対して、時刻\(t\)での波動関数の電子ニュートリノの成分の振幅は
\[\langle \nu_e \vert \nu_e \rangle_t = \cos^2 \theta e^{-iE_1 t/ \hbar} + \sin^2 \theta e^{-iE_2 t / \hbar}\]と表されます。 同じ運動量\(p\)に対するエネルギーの違いは、質量\(m_1, m_2 (\ll p / c)\)の差から
\[E_2 - E_1 = \sqrt{c^2 p^2 + m_2^2 c^4} - \sqrt{c^2 p^2 + m_1^2 c^4} \simeq \frac{(m_2^2 - m_1^2) c^4}{2E} = \frac{\Delta m^2 c^4}{2E}\]となります。 ニュートリノはほぼ光速度で運動するため、距離\(R\)離れたところで観測したとき(\(t=R/ c\))、\(t=0\)で電子ニュートリノだったものを電子ニュートリノとして観測する確率は
\[\vert \langle \nu_e \vert \nu_e \rangle_t \vert^2 = 1 - \sin^2 2\theta \sin^2 \left(\frac{\pi R}{L_V}\right)\]と表されます。 ここで
\[L_V \equiv \frac{4\pi E\hbar}{\Delta m^2 c^3} \simeq 2.48 \left( \frac{E}{1\mathrm{MeV}}\right) \left( \frac{1\mathrm{eV}^2}{\Delta m^2}\right) \ [\mathrm{m}]\]はvacuum oscillation length (真空振動長?)と呼ばれるものです。 極端に小さな質量差 (\(\Delta m^2 < 10^{-8} \mathrm{eV}^2\))でない限り、\(L_V\)は太陽半径より小さく、地球に到達するまでに何度も振動していることが期待されます。 太陽内部の種々の場所で発生したニュートリノが地球に到達するので、電子ニュートリノとして観測される確率は、上で求めた式の平均値
\[\overline{\vert \langle \nu_e \vert \nu_e\rangle_t \vert^2} = 1 - \frac{1}{2} \sin^2 2\theta\]と表されます。 このように、vacuum neutrino oscillationsにより、最大(\(\theta= \pi/4\)のとき)で電子ニュートリノを半分にまで減らすことができます。 またはちょうど良い小さな質量差(\(\Delta m^2 \sim 10^{-10} \mathrm{eV}^2\))を仮定して、地球の位置 (\(R = 1 \mathrm{AU}\))で観測に合うようにすることもできます。
MSW (Mikheyev-Smirnov-Wolfenstein) 効果
太陽ニュートリノ問題の解決として注目されている理論に、MSW効果 (またはmatter-enhanced neutrino flavour conversion)があります。 Vacuum neutrino oscillartionsの場合とは異なり、電子ニュートリノの残存率に下限はなく、採用するパラメータによっては全ての電子ニュートリノが\(\mu\)ニュートリノに変化することが可能です。 実際に観測されているニュートリノは、vacuum oscillationとMSW効果との両方の影響を受けていると考えられます。
太陽中心部のような密度の高いところでは、電子ニュートリノは電子との散乱の効果により、質量の高い状態になっています。 これに対して、\(\mu\)ニュートリノは太陽内部の物質と相互作用をしないため、その質量は真空中と同じ質量を持ちます。 電子ニュートリノの真空中の質量は\(\mu\)ニュートリノの質量よりも小さいため、その質量差が十分小さければ、太陽中心部では電子ニュートリノの質量の方が\(\mu\)ニュートリノの質量よりも大きくなっています。 そのような関係が成り立っている場合、太陽中心部で発生した電子ニュートリノの質量は、中心から表面に向かって移動するにつれて減少し、あるところで\(\mu\)ニュートリノの質量と同じになります。 その状態の交差点で、質量固有状態は連続的に真空中での高い質量状態、すなわち\(\mu\)ニュートリノのフレーバー状態につながっています。 したがって、その質量固有状態のままで交差点を通過すると、電子ニュートリノだったフレーバーが太陽表面では\(\mu\)ニュートリノになってしまう、というのがMSW効果です。
このMSW効果とvacuum oscillationsを考慮すると、地球での電子ニュートリノの残存率は、質量差\(\Delta m^2\)と混合角\(\theta\)およびニュートリノのエネルギーの関数として求められます。 このMSW効果を考慮した太陽ニュートリノフラックの理論値と、\({}^{37} \mathrm{Cl}\)、神岡、ガリウム(GALLEX/GNO, SAGE)測定値の矛盾がないためには、\(\Delta m^2 - \theta\)図上の次の3つの領域が許容されます。
それぞれの場合において、ニュートリノのエネルギースペクトルは異なっています。 後述のSNOの結果を考慮すると、大きな混合角の解がより良さそうなことがわかります。
Subbury Neutrino Observatory (SNO)
MSW効果が実際に起こっているかを明らかにする可能性のある装置が、1999年にカナダのオンタリオ州のSudbury近くのCreightonニッケル鉱山の2000m地下に設置されました。 透明な厚さ5cmのアクリル板に囲まれた、直径12mの球に1000トンの重水を入れ、その周りに9600個の光電管をつけたチェレンコフ光検出装置です。

この装置は、カミオカンデが検出可能なニュートリノによる電子散乱の他に
\[\nu_e + {}^2 \mathrm{H} \ \longrightarrow \ \mathrm{p} + \mathrm{p} + \mathrm{e}^- \quad (Q = -1.44 \mathrm{MeV}; E_\mathrm{th} \sim 6 \mathrm{MeV}; \mathrm{cc})\] \[\nu_x + {}^2 \mathrm{H} \ \longrightarrow \ \nu_x + \mathrm{p} + \mathrm{n} \quad (Q = -2.2 \mathrm{MeV}; E_\mathrm{th} \sim 2.2 \mathrm{MeV}; \mathrm{nc})\]の反応が検出できます。 1番目の反応では、電子の発するチェレンコフ光が観測されます。 この反応では電子ニュートリノのみが検出されます。 一方、2番目の反応はニュートリノの種類に依らず起こります。 そのため他の反応との比較により、地球に届く電子ニュートリノと\(\mu\)ニュートリノとの比を知ることができます。 ここから、ニュートリノ振動により電子ニュートリノが他のフレーバーのニュートリノに変化したかどうかを検証することができます。 このnc反応で放出される中性子を測定するのに、3通りの方法が取られました。 最初の1年では純粋な重水中で、中性子が重水素に確率25%で捉えられるときに発生する6.25MeVのガンマ線を測定するというものです。 次の年には2.5トンの塩 (NaCl)を加え、Clが中性子を確率83%で捕獲する反応で放出される8.6MeVのガンマ線を測定し、中性子捕獲効率を上げました。 さらに3年面には、溶かされた塩を取り出して純粋な重水に戻し、\({}^3 \mathrm{He}\)が詰まったproportional counter (比例計数管)を検出器内に入れて中性子をカウントしました。
この装置は1999年11月から観測を開始し、これまでに純粋な重水による観測とNaClを入れたnc反応に対する感度をあげた観測まで行われました。 これまでの観測によるcc反応・電子散乱(es)反応・nc反応によるニュートリノフラックスの測定値は、\(10^6 / (\mathrm{cm^2 \ s})\)の単位で
という結果を得ました。 電子散乱(es)反応によるニュートリノフラックスは、スーパーカミオカンデの結果とよく一致していることが知られています。 またニュートリノフレーバーに依存せず起こるnc反応によるニュートリノフラックスの値が、\({}^8 \mathrm{B}\)ニュートリノの総フラックスを表しており、太陽モデルの値と比較すべき値となります。 この値は、元素の拡散を考慮した太陽モデルの値と一致していることも判明しています。
nc反応によるニュートリノフラックスの値は、電子ニュートリノだけが起こるcc反応および主に電子ニュートリノが起こすes反応からのニュートリノフラックスに比べて大きくなっています。 これは、電子ニュートリノが太陽中心から放出されて地球に到達するまでに、かなりの割合がニュートリノ振動によって他のフレーバーのニュートリノに変化したことを明らかにしています。 これらの結果から求められたニュートリノのパラメータは、\(\Delta m^2 = 8.0_{-0.4}^{0.6} \times 10^{-5} \mathrm{eV}^2, \theta = 33.9_{-2.2}^{2.4} \mathrm{degree}\)となっています。
ニュートリノのエネルギースペクトルがほとんど修正されていないことも、大きな混合角の結果と一致します。
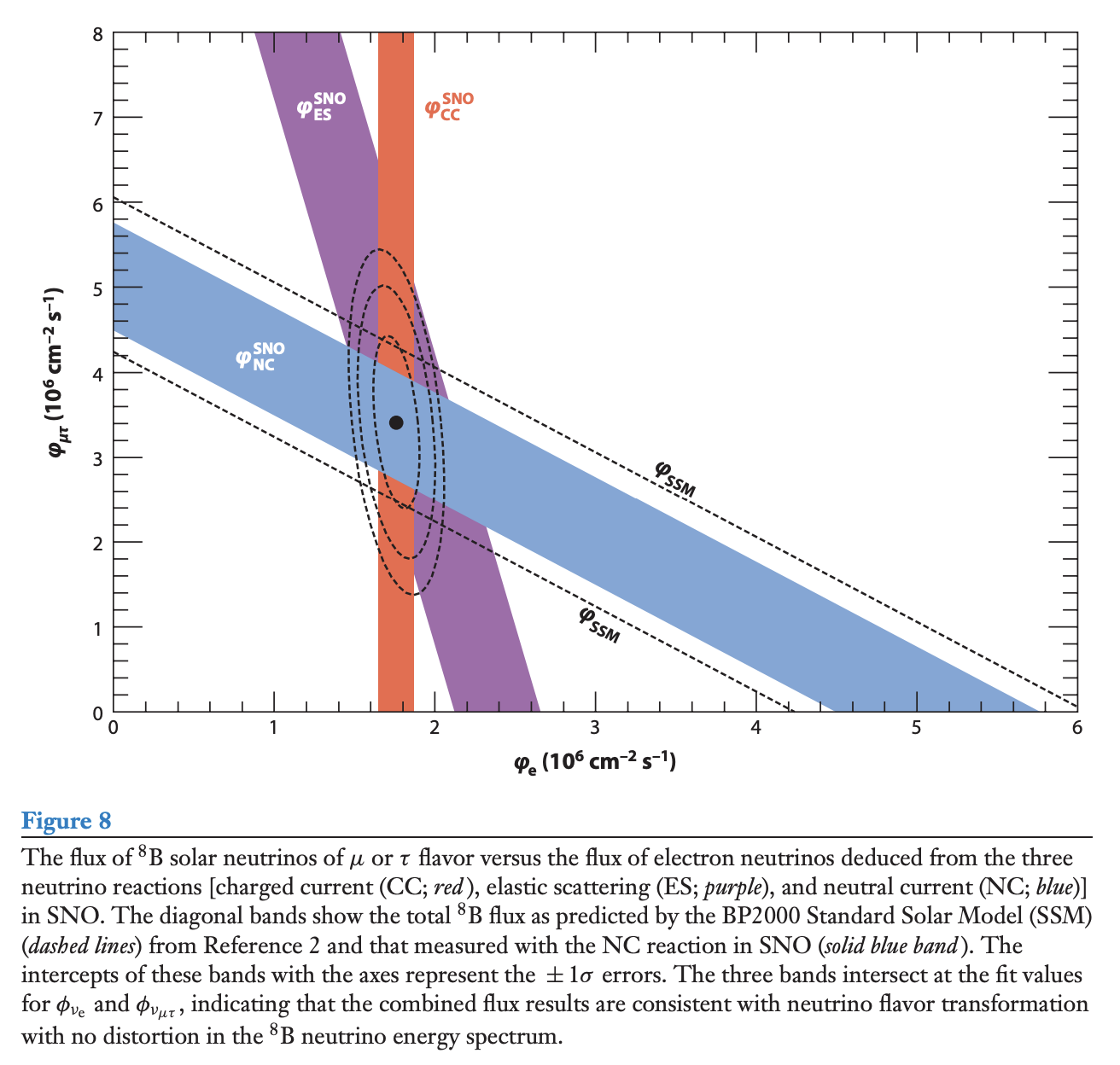
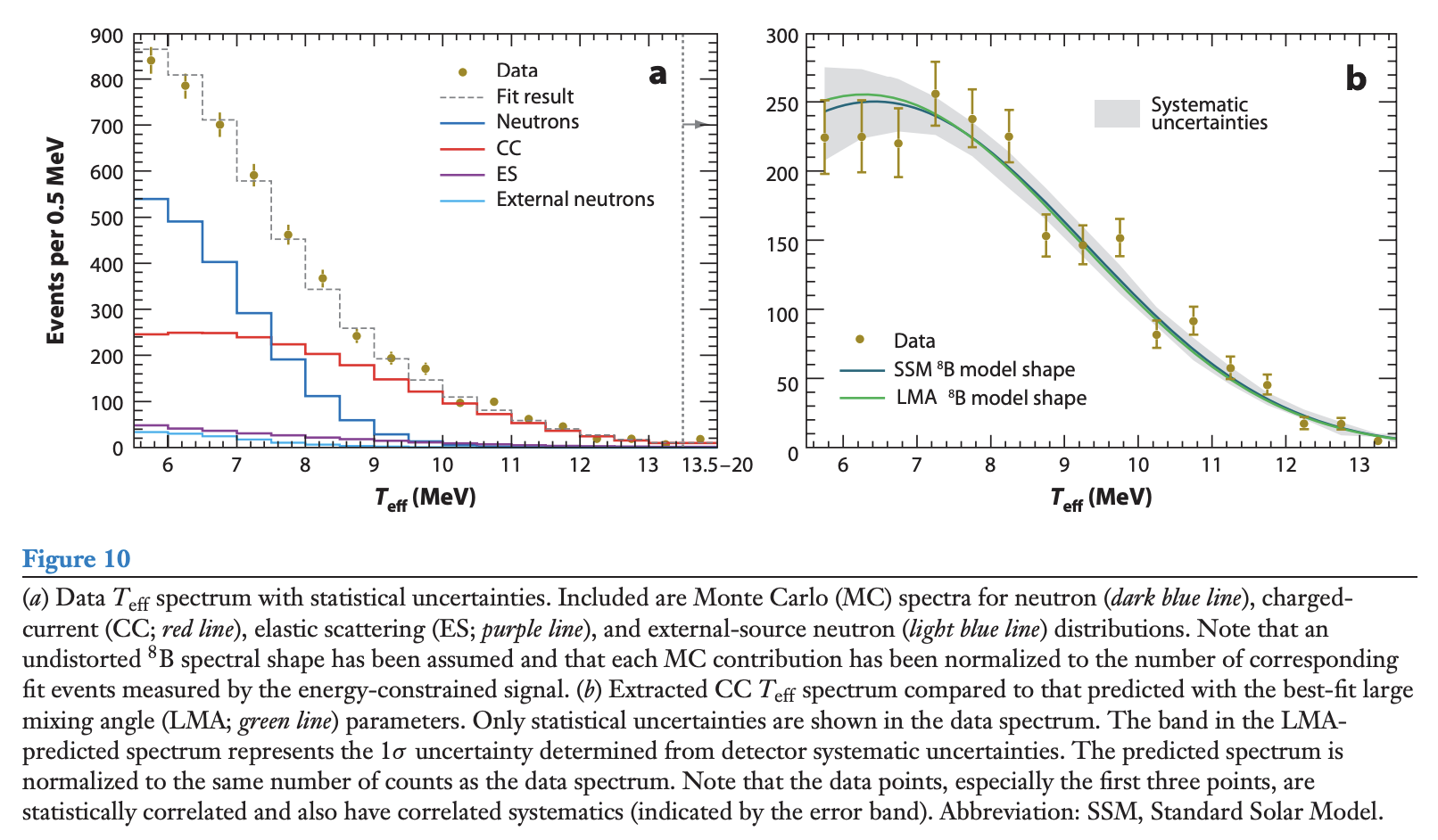
このSNOは、Arhur B. McDonaldに2015年ノーベル物理学賞をもたらしたことでも有名です。
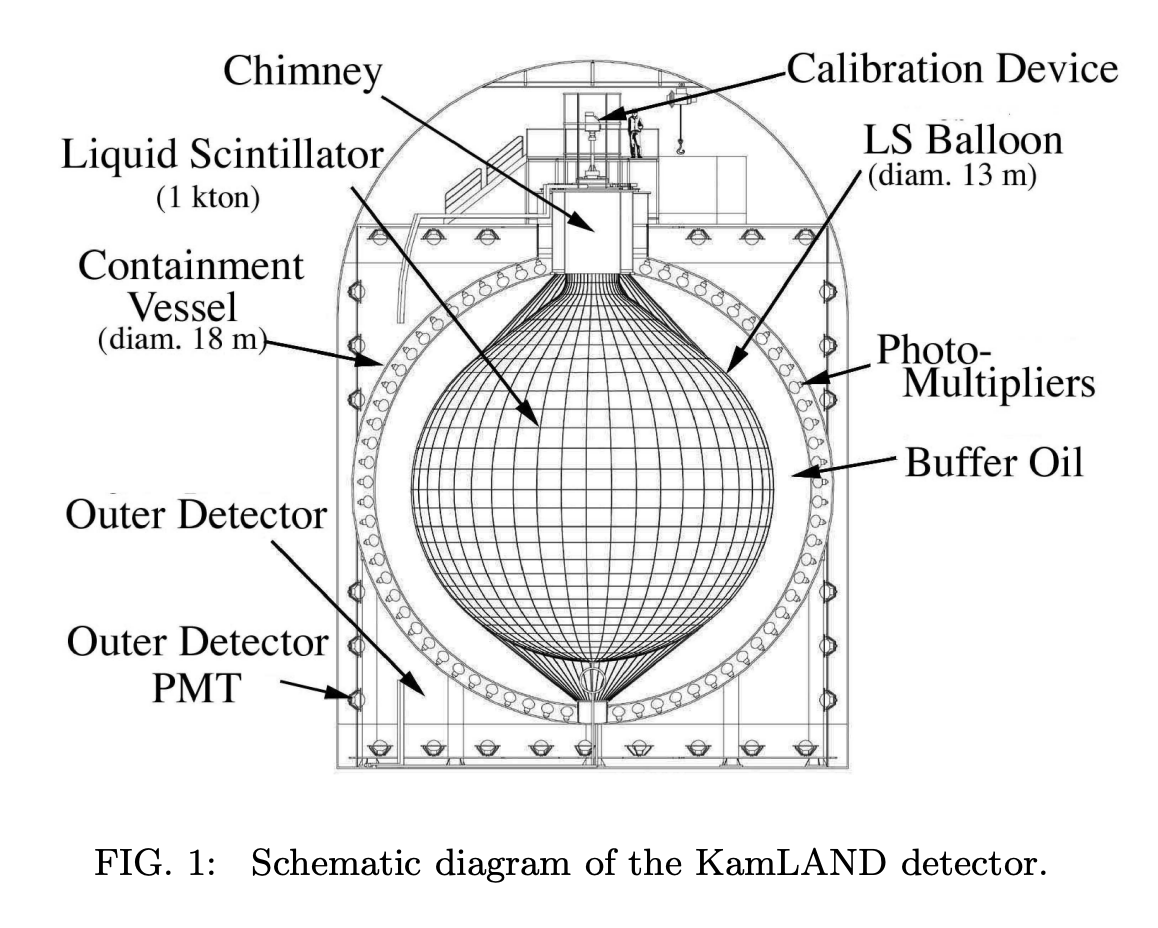
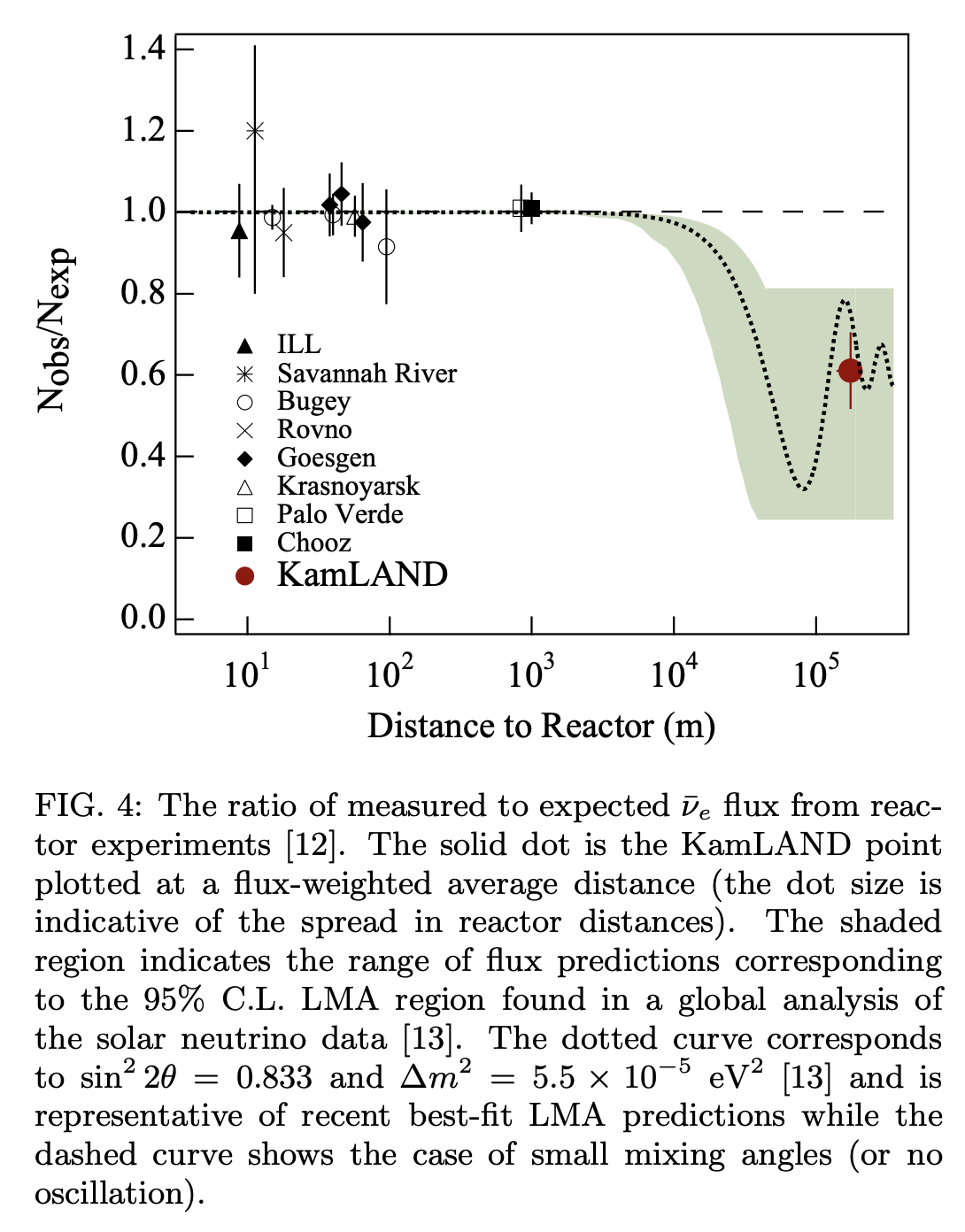
カムランド (KAMioka Liquid scintilator ANtineutrino Detector)
遠くの原子炉からの電子反ニュートリノ (\(E \sim 9 \mathrm{MeV}\))を\(\bar{\nu}_e + \mathrm{p} \rightarrow \mathrm{e}^+ + \mathrm{n}\)を利用して検出することにより、ニュートリノ振動を検証する目的で作られました。 この結果は、太陽ニュートリノで得られた結果とよく一致しています。
将来計画: ハイパーカミオカンデ
さらに、東京大学と高エネルギー加速器研究機構(KEK)を中心として、神岡に新しい実験施設であるハイパーカミオカンデが計画されています。
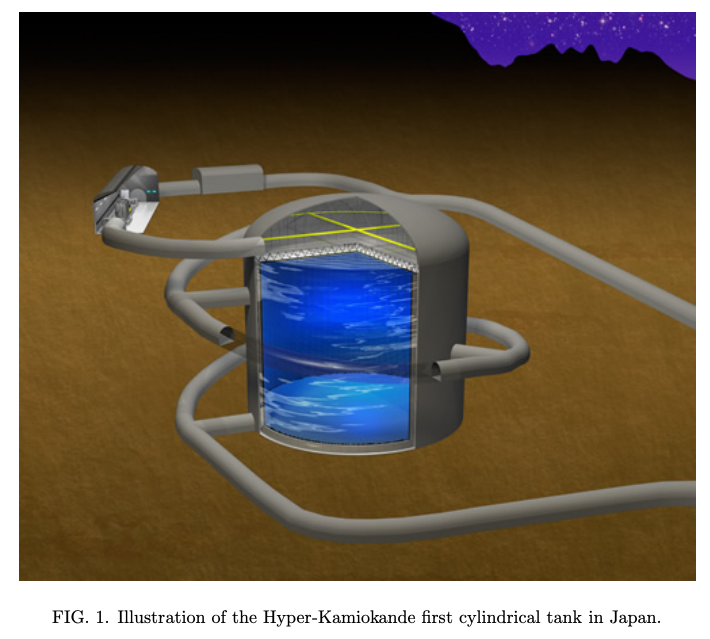
純水量を5倍以上に増やすなどの改良を行い、スーパーカミオカンデでは達成できなかった太陽黒点の11年の活動周期との相関を探るなど、太陽エネルギー源と太陽の進化の解明を目指します。
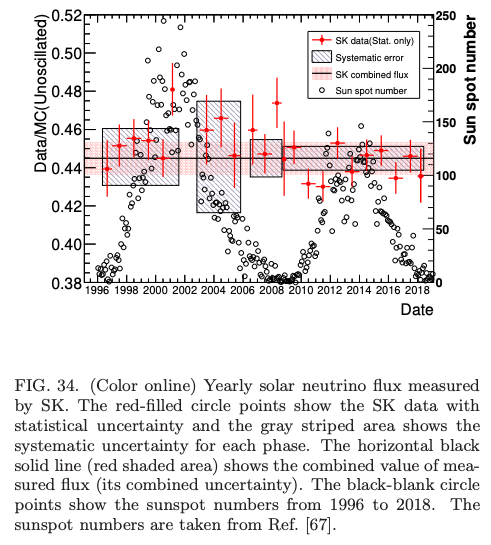
このほかにも、ハイパーカミオカンデでは以下のような物理の解明に向けた測定・観測も予定されています。
- CP対称性の破れの測定
- ニュートリノ質量階層構造の測定
- 超新星爆発からのニュートリノ観測
- 超新星背景ニュートリノの観測
- 暗黒物質から発生するニュートリノの観測
- 陽子崩壊探索
最近の太陽元素組成の改訂
Apslund et al. (2004)は、太陽表面の対流についての3次元モデルを用い、粒状斑による表面温度の不均一性が吸収線に及ぼす効果と、non-LTE効果を考慮した解析により、太陽表面お酸素含有量がこれまで使われていた値の60%程度しかないという結果を得ました。 他の元素に対する同様の解析によっても、これまでの値よりも少ない傾向となることがわかっています。 この改訂された元素組成によると、太陽表面の質量重元素含有量は従来よく採用されてきた\(Z = 0.018 \sim 0.019\)よりもかなり少ない\(Z \sim 0.0126\)となります。
この元素組成の改訂は、太陽モデル、特に外層モデルに大きな影響を及ぼします。 2008年当時、改訂された元素組成に基づく標準太陽モデルは、太陽振動(Helioseismology)から推測される太陽内部の音速分布や対流層の深さなどと、あまりよく会わない結果となりました。 改訂された元素組成に基づく太陽モデルについての詳細な議論は、Basu & Antia (2008)などで与えられています。
改訂された太陽元素組成は、太陽モデルのニュートリノフラックス予想値にも影響を与えます。 CNO元素含有量が減少したこと、そして不透明度の減少による中心温度のわずかな減少により、新元素組成に基づく標準太陽モデルではCNO反応からのニュートリノフラックスが大きく減少します。 また中心温度の減少により、\({}^8 \mathrm{B}\)ニュートリノフラックスも20%程度減少し、SNOによる\({}^8\mathrm{B}\)フラックス (\(\phi_\mathrm{nc} = 5.09 \pm 0.43\))よりも、多少小さな値となります。
以前から、太陽の酸素含有量が太陽近傍の恒星に比べて以上に大きいことが問題になっていました。 しかしこの太陽元素組成の改訂によって酸素含有量が小さくなったために、ヘリウム含有量と酸素含有量との関係が、系外銀河のものと同じになりました (He/H=44.6 O/H + 0.075。) すなわち、太陽の元素組成は周りの銀河と同様の化学進化の結果であると考えることができ、銀河の化学進化については、この太陽元素組成の改訂によって長年の懸念が解決したことになります。

さらに最近、同じ研究チームがこの研究をアップデートしました。 Apslund et al. (2021)では恒星大気モデルの3次元計算を新しくするなどの改良を行い、さらに詳細なモデル計算を行いました。 すると表面での重元素含有量は\(Z \sim 0.0139\)となり、これまでの同様の計算で求められていたC, N, Oの含有量より小さなものとなりました。
参考文献
[1] Anandaram, 2014, “On the Tachocline Zone Location in the Sun, the Luminosity Transport time scale, the Rotational Inertia and their Time Variation in Standard Solar Evolution Models”
[2] Kosovichev et al., 1997, “Structure and Rotation of the Solar Interior: Initial Results from the MDI Medium-L Program”
[3] Turck-Chize et al., 2004, “Surprising Sun: A New Step Towards a Complete Picture?”
[4] Cleveland et al., “Measurement of the Solar Electron Neutrino Flux with the Homestake Chlorine Detector”
[5] Nakahata, 2022, “History of Solar Neutrino Observations”
[6] Abe et al., 2024, “Solar neutrino measurements using the full data period of Super-Kamiokande-IV”
[7] GNO Collaboration, 2005, “Complete results for five years of GNO solar neutrino observations”
[8] Abdurashitov et al., 2002, “Solar neutrino flux measurements by the Soviet-American gallium experiment (SAGE) for half the 22-year solar cycle”
[9] Jelly et al., 2009, “The Subdury Neutrino Observatory”
[10] KamLAND Collaboration, 2003, “First Results from KamLAND: Evidence for Reactor Antineutrino Disappearance”
[11] Hyper-Kamiokande Proto-Collaboration, 2018, “Hyper-Kamiokande Design Report”
[12] Asplund et al., 2021, “The chemical make-up of the Sun: A 2020 vision”
[13] 太陽の科学館
[14] SOHO
[15] 天文学辞典, “5分振動 (太陽の)”
[16] 柴橋博資, 高田将郎, “太陽の内部を音波で見る”
[17] ハイパーカミオカンデ
[18] Kippenhahn, Weigert & Weiss, “Stellar Structure and Evolution”
[19] 野本憲一, 定金晃三, 佐藤勝彦, “恒星”
[20] 桜井隆, 小島正宜, 小杉健郎, 柴田一成, “太陽”