Table of contents
ヘリウム燃焼殻の熱的不安定性
AGB星の中で起こるヘリウム殻燃焼は熱的に不安定で、燃焼の暴走(フラッシュ)を起こします。 ここではその原因と現象について見ていくことにしましょう。
導出
この熱的不安定性は、気体の状態方程式が原因ではなく、幾何学的効果によるものです。 よって以下では、簡単のため理想気体を仮定しましょう。 下左図のように、幾何学的に薄い燃焼殻を考えます。
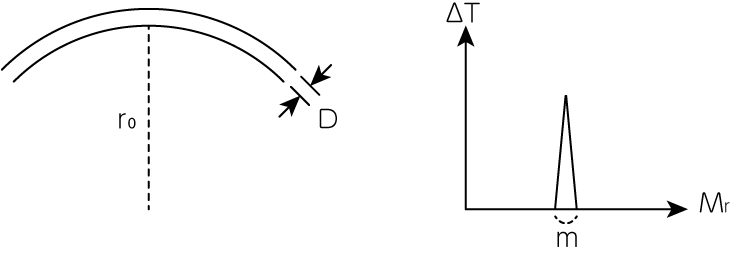
その燃焼殻の恒星中心からの距離を\(r_0\)とし、その幾何学的厚みを\(D (\ll r_0)\)とします。 その燃焼殻に含まれる質量を\(m\)とすると
\[m = 4\pi r_0^2 D \rho \tag{1}\]となります。 このような燃焼殻の熱的安定性を調べることにします。 (1)式のLagrangian perturbation (ラグランジュ的な摂動)をとると
\[m = 4\pi r_0^2 (D + \Delta D) (\rho + \Delta \rho) = 4\pi r_0^2 (D \rho + D \Delta \rho + \Delta D \rho) \tag{2}\]より
\[\frac{\Delta D}{D} = - \frac{\Delta \rho}{\rho} \tag{3}\]が得られます。 この殻の外側では、相同な摂動になっていると仮定します。 すると(8.5.13)式より
\[\frac{\Delta P}{P} = -4 \frac{\Delta r}{r} = -4 \frac{\Delta D}{r_0} = -4 \frac{D}{r_0} \frac{\Delta D}{D} \underbrace{=}_{(3)} 4 \frac{D}{r_0} \frac{\Delta \rho}{\rho} \tag{4}\]のようになります。 \(D/r_0 \ll 1\)と(3), (4)式より
\[\left\vert \frac{\Delta P}{P} \right\vert \ll \left\vert \frac{\Delta \rho}{\rho} \right\vert \tag{5}\]を得ます。 これは幾何学的に薄い燃焼殻が膨張しても、他の場所の力学平衡の構造にはほとんど影響しないことを表しています。 圧力変化が密度変化に比べて非常に小さいことを、理想気体の状態方程式\(P \propto \rho T\)に適用すると
\[\frac{\Delta T}{T} \simeq - \frac{\Delta \rho}{\rho} \tag{6}\]が得られます。 恒星全体が相同に変化する場合には
\[\frac{\Delta T}{T} = \frac{4-3\chi_\rho}{3\chi_T} \frac{\Delta \rho}{\rho}\]のように膨張する(\(\Delta \rho < 0\))と温度が下がる(\(\Delta T < 0\))関係でしたが、薄い殻の場合には、(6)式から膨張すると温度が上昇する(\(\Delta T >0\))関係にあるとわかります。 この関係を用いて、幾何学的に薄い燃焼殻の比熱\(C_\mathrm{s}\)を求めてみましょう。 \(TdS = C_V dT + P d(1/\rho)\)と(6)式より
\[C_\mathrm{s} \Delta T = T \Delta S = C_V \Delta T - \frac{P}{\rho} \frac{\Delta \rho}{\rho} = \left( C_V + \frac{P}{\rho T}\right) \Delta T = \frac{5}{3} C_V \Delta T \tag{7}\]が得られます。 これは、燃焼殻の比熱が\(\frac{5}{3} C_V\)という正の値を持つことを表しています。 ヘリウムフラッシュでは、電子の縮退によって比熱が正の値になるのでした。 しかし薄い殻の場合には幾何学的な効果により、圧力変化が密度変化に比べて小さくなることで、比熱が正の値を持つようになります。
ヘリウムフラッシュで得られたエネルギー保存と、輻射によるエネルギー輸送に対する線形摂動の式(8.5.8)、そして(8.5.9)式をこれまで求めた関係(6), (7)式、そして\(\vert \Delta D / r_0 \vert \ll \vert \Delta \rho / \rho \vert\)であることを使って書き換えましょう。
ここで、摂動量の時間依存性は\(\Delta f \propto e^{st}\)と仮定されており、\(s\)が正の値のとき、熱的不安定が起こることを意味します。
(8)式を(9)式に代入し、\(\Delta L_r/ L_r\)を消去しましょう。 このとき、\(\kappa_T, \kappa_\rho, \frac{d\ln T}{dM_r}\)などの量の\(M_r\)に対する依存性は、\(\left\vert \frac{d(\Delta T / T)}{dM_r}\right\vert\)に比べて小さいとして無視します。 また\(\epsilon_T \gg \epsilon_\rho\)であることも考慮します。 すると
が得られます。 この式を簡単化するために、温度の摂動を最初の右図のように、燃焼殻に局在した形で考えることにしましょう。 すると、殻内での平均量にバーをつけて表したとき
\[\overline{\frac{\partial}{\partial M_r} \left( \frac{\Delta T}{T} \right)} \sim 0 \tag{11}\] \[\overline{\frac{\partial^2}{\partial M_r^2} \left( \frac{\Delta T}{T}\right)} \simeq \frac{\overline{-\frac{\Delta T}{m/2} - \frac{\Delta T}{m/2}}}{mT} = - \frac{4}{m^2} \frac{\overline{\Delta T}}{T} \tag{12}\]これらの関係を用いて、(10)式を燃焼殻で平均化すると
\[s \frac{C_\mathrm{s}}{L} \simeq \frac{\epsilon_\mathrm{n}}{L} (\epsilon_T + \kappa_T - \kappa_\rho - 4) + \frac{4}{m^2} \frac{1}{\frac{d\ln T}{dM_r}} \tag{13}\]が得られます。
光度\(L\)はほとんど燃焼殻のみで生成されるので
と考えることができます。 これを(13)式に用いれば
\[s \simeq \frac{L}{C_\mathrm{s} m} \left( \epsilon_T + \kappa_T - \kappa_\rho - 4 - \frac{4}{m \left\vert \frac{d\ln T}{dM_r}\right\vert}\right) \tag{15}\]が得られます。 この式で出てくる\(C_\mathrm{s} m\)は燃焼殻全体の比熱、\(C_\mathrm{s} m /L\)は燃焼殻の熱的タイムスケールを表しています。 \(s>0\)となって不安定性が起こる時は、熱的タイムスケール程度で起こることが保証されています。 幾何学的に薄い燃焼殻では、(7)式より\(C_\mathrm{s}>0\)です。 よって上式の\((\cdots )\)の中が正の値になれば、不安定性が起こることになります。 完全電離したガスでは\(\kappa_T = \left( \frac{\partial \kappa}{\partial T}\right)_\rho<0\)であるため、温度上昇に伴うエネルギー発生率の増加の効果を表す\(\epsilon_T\)だけが、不安定性を誘発する要因になっています。 \((\cdots )\)の中の残りの項は、温度が燃焼殻内で上昇したときに、輻射によるエネルギーの散逸率が増加する効果を表しています。 すなわち摂動によって温度が上昇したときに、核融合反応の活発化によるエネルギー発生率の増加と、輻射によるエネルギー散逸率の増加のどちらが優勢となるかで、熱的不安定性が起こるかどうかが決定されます。 \(\kappa_T - \kappa_\rho\)は、(6)式より温度が上昇して膨張すると、不透明度が減少してエネルギーが流されやすくなることを表しています。 また\(m \left\vert \frac{d\ln T}{dM_r} \right\vert\)は、平衡構造での燃焼殻の内部側と表面側との相対温度差を表します。 \(\frac{4}{m \vert d\ln T / dM_r \vert}\)は、質量\(m\)の燃焼殻にエネルギーが溜まったときに、それを輻射によってならす効果を表します。 \(m\)が小さいほど、摂動による温度勾配変化が大きく、エネルギー散逸の効率が良い(熱が矯められにくい)ことを意味します。
まとめると、燃焼殻の不安定性は幾何学的に薄く\((\vert \Delta P / P \vert \ll \vert \Delta \rho / \rho \vert )\)、しかしエネルギーを溜め込むことができるほどの厚さを持ち、また原子核燃焼によるエネルギー発生率の温度依存性が大きいほど、起こりやすいことがわかります。 この不安定性の代表例はAGB星のヘリウム燃焼殻で起こるもので、熱的パルス (またはヘリウム殻フラッシュ)と呼ばれています。 理想気体の下での水素燃焼殻については merginal (安定と不安定のちょうど境目?)で、線形安定性解析では不安定と予想されていますが、恒星進化モデルでは確認されていません (新星爆発における水素殻燃焼の暴走は、電子の縮退の効果が大きいため、これと発火機構が異なります。)
熱パルス (ヘリウム殻フラッシュ)
AGB星のヘリウム燃焼殻が熱的不安定星を起こすと、エネルギー発生率が急激に大きくなります。 すると輻射でエネルギーを流すには温度勾配が断熱温度勾配を越えることになり、燃焼殻外側に対流層が発生します。 対流層は、水素燃焼殻とヘリウム燃焼殻との間のヘリウム層の大部分に広がることで、ヘリウム燃焼の生成物がその領域で混合されることになります。 また対流の発生により、エネルギーが効率よく運ばれるようになるため、フラッシュは収束に向かい、それ以上暴走することはありません。
ヘリウム殻フラッシュが起こると、発生したエネルギーでヘリウム燃焼殻の外側のヘリウム層が膨張します。 そのため水素燃焼殻の温度が下がり、水素燃焼によるエネルギー発生率\(L_\mathrm{H}\)が減少します。 フラッシュが起きていない期間では\(L_\mathrm{H} \gg L_\mathrm{H_e}\)なので、殻フラッシュ起きると、表面での光度は逆に減少します。 \(L_\mathrm{H_e}\)のピーク値は、殻燃焼の起こる\(M_r\)が大きいほど大きくなり、\(L_\mathrm{H_e}\sim 10^8 L_\odot\)にもなります。 しかしそのエネルギーは外側の層に吸収され、表面には平均化されて出てきます。
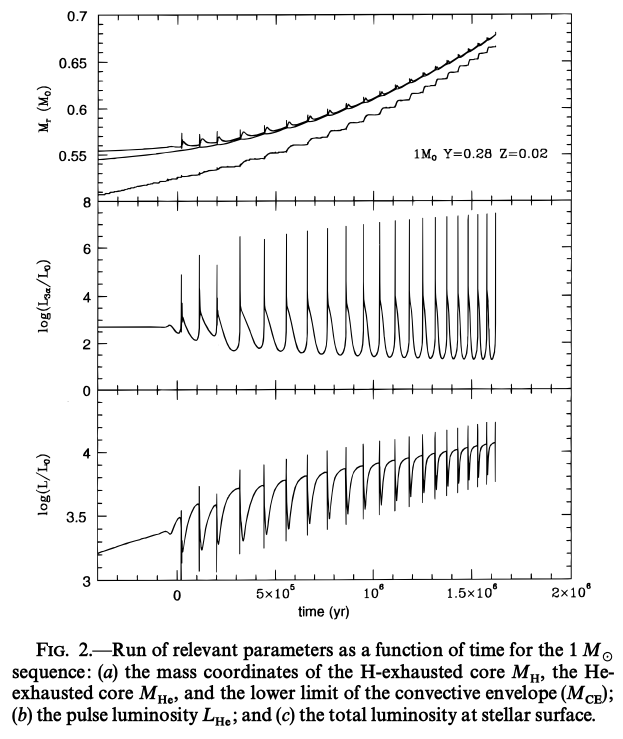
Straniero et al. (1997)より、\(1M_\odot\)の質量変化・パルス光度\(L_\mathrm{H_e}\)・恒星表面からの全光度を描画したもの
殻フラッシュが起こり膨張して水素燃焼殻付近の温度が下がると、対流外層の底が、それまで水素燃焼殻であったところよりも深く侵入してきます。 その時点では\(L_\mathrm{H_e}\)は小さくなっており、ヘリウム層の対流殻は消えています。 しかし対流外層の底の侵入により、かつては対流殻内にあったため、殻フラッシュで起きた核反応生成物を含んでいる領域の一部が対流外層に取り込まれ、混合されて表面にも現れてきます。 この現象はthird dredge-upと呼ばれています。
対流殻内では、トリプルα反応により主に炭素ができており、またs過程中性子捕獲による生成元素が含まれています。 AGB星の中でs過程の豊富な恒星や、酸素よりも炭素の含有量の多い(C/O>1)炭素星は、熱パルスに伴うthird dredge-upの効果で生まれるとされています。
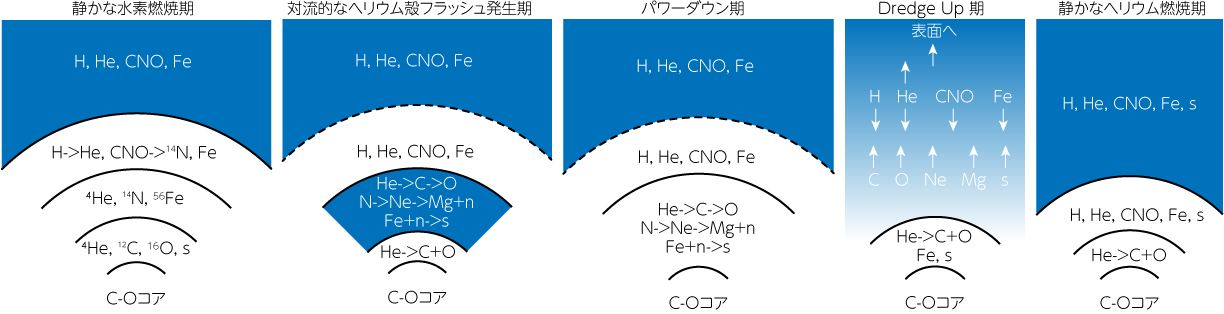
Iben (1985)の図を改訂
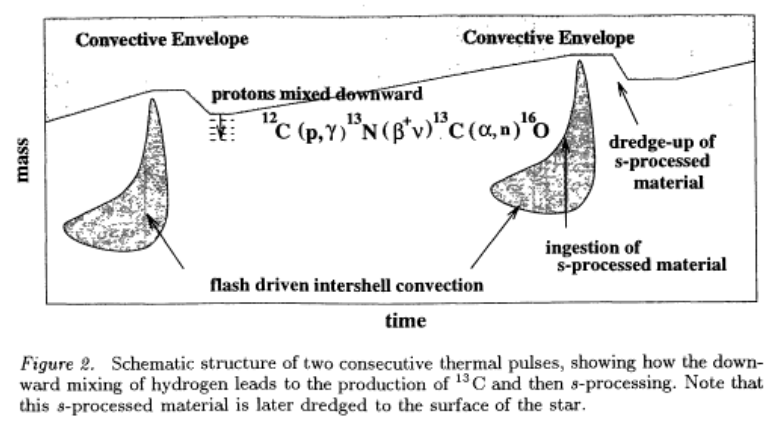
Lattanzio & Frost (1997)より、熱パルスにより発生した対流層の時間発展の概念図
参考文献
[1] Straniero et al., 1997, “Evolution and Nucleosynthesis in Low-Mass Asymptotic Giant Branch Stars. I. Formation of Population I Carbon Stars”
[2] Iben, 1985, “The Life and Times of an Intermediate Mass Star - in Isolation/in a Close Binary”
[3] Lattanzio & Frost, 1997, “The asymptotic giant branch”
[4] Kippenhahn, Weigert & Weiss, “Stellar Structure and Evolution”
[5] 野本憲一, 定金晃三, 佐藤勝彦, “恒星”